2.一个垂钓俱乐部鼓励垂钓者将钓上的鱼放生，打算按照放生的鱼的质量给予奖励，俱乐部只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的质量的方法．假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据(胸围指鱼身的最大周长)：

身长/cm	36.8	31.8	43.8	36.8	32.1	45.1	35.9	32.1
质量/g	765	482	1162	737	482	1389	652	454
胸围/cm	24.8	21.3	27.9	24.8	21.6	31.8	22.9	21.6

先用机理分析建立模型，再用数据确定参数。

机理分析：

根据我们的常识，鱼越大越重，鱼的身长和胸围都是用来描述鱼的大小的一个物理量，所以我们可以探究软尺能测量的鱼的身长以及胸围（鱼身的最大周长）与鱼的质量的关系，用鱼的身长以及胸围来对其质量进行估计。

模型假设：

根据钓上来的8条鱼的身长，质量，胸围的数据进行分析，结合实际情况做出以下合理的简化假设

1. 由于鱼池中只有一种鱼（即鲈鱼），这些鱼的形状大致相同，其整体形状是相似的，其横截面也是相似的，所以鱼的质量（M）与其身长（l）的立方成正比，同时也与其胸围（d）的平方成正比。
2. 肥鱼与瘦鱼同等看待，鱼的密度也是一样的。

模型建立：

根据模型的假设我们很容易可以得到：

M：质量  l ：身长  d：胸围  k1，k2：比例系数

M=k1l3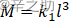                         -----（1）

M=k2d2l                        -----（2）

模型求解：

     根据8条鱼的身长，质量，胸围的数据，大致可以算得k1=0.0146，k2=0.0322

M=0.0146l3

M=0.0322d2l

将实际数据与我们建立的模型结果进行对比：

实际	765	482	1162	737	482	1389	652	454
模型一	727	469	1226	727	483	1339	675	483
模型二	730	465	1100	730	483	1471	607	483

基本上大致吻合，固可以用
M=0.0146l3

M=0.0322d2l

通过测量鱼的身长和胸围来估算鱼的质量。

---

     3.用已知尺寸的矩形板材加工半径一定的圆盘，给出几种简便，有效的排列方法，使加工出尽可能多的圆盘。

机理分析：

根据我们的常识可以知道切割材料，材料不一定能全部用完，会产生一些浪费，那么怎么切割，怎么布局模具来加工更多就需要制定不一样的方案来比较不同切割方法的优劣。

模型假设：

1. 切割时不会产生误差，圆盘之间以及圆盘和板材之间均可以相切，且不会出现切多切少的问题。
2. 圆盘的半径为单位1，矩形板材的长为a，宽为b。

 

模型建立：

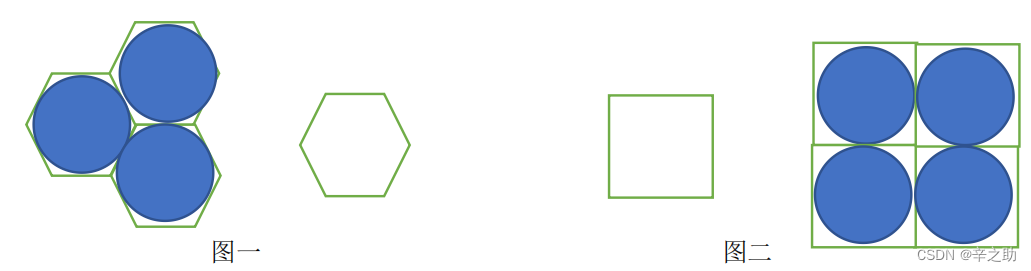
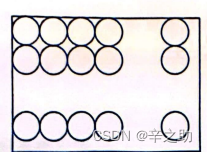
方案一：圆盘中心按六角形排列，如图一。

方案二：圆盘中心按正方形排列，如图二。

模型求解：

N1：方案一能裁剪的圆盘总数

N2：方案二能裁剪的圆盘总数

a :  矩形板材的长

b： 矩形板材的宽

m:  方案一能排列的行数

 

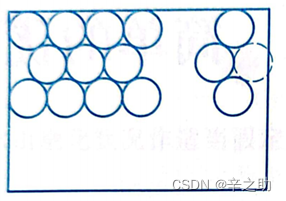
方案一：

行数m根据几何解析可得出2+（m-1）√3≤a

所以m的最大值是[ a-2√3 ] + 1

N1=m b -12 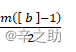        m为偶数

N1=m b -12+ 12 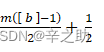    m为奇数，[ b ]为偶数

 

方案二：

N2=[ a2 ]*[ b2 ]

两个方案的(N1/N2)比较表如下:

a\b	3	5	8	10	14	20
4	2/2	4/4	7/8	9/10	13/14	19/20
7	3/3	6/6	11/12	14/15	20/21	29/30
10	5/5	10/10	18/20	23/25	33/35	48/50
15	8/7	16/14	28/28	36/35	52/49	76/70
20	11/10	22/20	39/40	50/50	72/70	105/100

理论最佳的（不考虑损失）:

a\b	3	5	8	10	14	20
4	3	6	10	12	17	25
7	6	11	17	22	31	44
10	9	15	25	31	44	63
15	14	23	38	47	66	95
20	19	31	50	63	89	127

方案一的有效利用率如下：

a\b	3	5	8	10	14	20
4	66.67%	66.67%	70%	75%	76.4%	76%
7	50%	54.55%	64.71%	63.63	64.52%	65.91%
10	55.56%	66.66%	72%	74.19%	75%	76.19%
15	57.14%	69.56%	73.68%	76.56%	78.79%	80%
20	57.89%	70.97%	78%	79.37%	80.90%	82.677%

方案二的有效利用率如下：

a\b	3	5	8	10	14	20
4	66.67%	66.67%	80%	83.33%	82.35%	80%
7	50%	54.55%	70.59%	68.18%	67.74%	68.18%
10	55.56%	66.66%	80%	80.65%	79.55	79.37%
15	50%	60.87%	73.68%	79.37%	74.24%	73..68%
20	52.63%	64.52%	80%	79.37%	78.65%	78.74%

当a，b较大时，总体来说方案一要优于方案二。

根据两个方案的有效利用率表可知：

当然当矩形板材的a，b均为偶数明显利用比优于a, b为二者中有奇数的情况

方案一的ab的最佳比为20r/20r.

方案二的ab的最佳比为4r/10r.

---

5.生物学家认为，对于休息状态的热血动物，消耗的能量主要用于维持体温，能量与从心脏到全身的血流量成正比，而体温主要通过身体表面散失，建立一个动物体重（单位：g）与心率（单位：次/min）之间关系的模型，并用下面的数据加以检验。

动物	体重	心率
田鼠	25	670
家鼠	200	420
兔	2000	205
小狗	5000	120
大狗	30000	85
羊	50000	70
人	70000	72
马	450000	38

     动物消耗的能量P主要用于维持体温，而体内热量通过其表面积S散失，记动物体重为w，则P正比于S,正比于w2/3，又因为P正比于血流量Q,而Q=qr,其中q是动物每次心跳泵出的血流量，r为心率，合理地假设q与w成正比，于是P正比于wr。综上可得r正比w-1/3,或r=kw-1/3。

由所给的数据可以算得k=2.0897*103

实际数据与模型结果比较如下表：

动物	实际心率/（次/min）	模型结果/（次/min）
田鼠	670	715
家鼠	420	357
兔	205	166
小狗	120	122
大狗	85	67
羊	70	57
人	72	51
马	38	27