统计与概率论本身与数据分析的关联度非常的高而且掌握的程度也可以很好的反映出从业者的投入程度。

接下来我们通过一些例子，来体验概率论思维。

扔十次硬币，真的会有五次朝上？

直觉上，我们知道抛硬币正反两面朝上的概率各一半，如果你真的现在去抛十次硬币，真的有5次正面向上的情况出现么？其实这种可能性只有1/4左右，显然和大多数人的直觉完全不同了。

我们都知道，统计学的规律只有经过了大量随机试验才能得出，也才有意义。但是随机试验得到的结果，和我们用古典概率算出来的结论可能是两回事。不仅你掷10次硬币大部分时候不可能得到五次正面朝上的结果，你做其它随机试验也是如此。

再比如比如你掷12次骰子，大约只有30%的情况它正好有两次六点朝上。这时你是否能讲，有70%的可能性要否定六点朝上的概率是1/6这个结论呢？似乎也不是这样的。

比如抛硬币，每次正面朝上的概率是1/2，事件A是“正面朝上”，它出现的概率每次也是1/2。当然事件B就是反面朝上，每次的概率也是1/2。在一般情况下，出现A的概率是p，B的概率是1-p。这类试验后来被称为伯努利试验。

好了，基本的设定讲清楚了。我们来分析一下掷硬币的问题。照理讲，我们掷10次硬币，正面朝上的次数应该是5次。但是如果你真的拿一个硬币去试试，你会发现可能只有3次正面朝上，也可能4次正面朝上，甚至会出现没有一次正面朝上的情况。

如果我们把从0次正面朝上，也就是说全部是背面朝上，到10次全是正面朝上的可能性都算出来，画成一个折线图，就是一个中间鼓起的曲线：

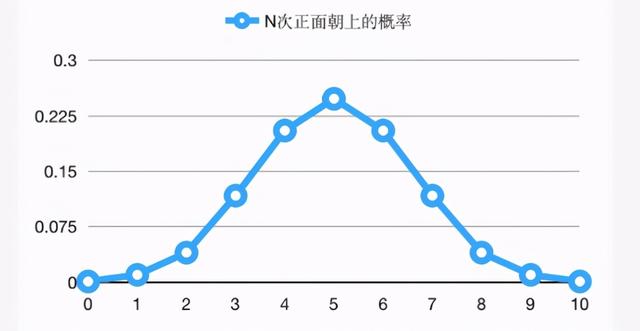
图中可以看出，虽然5此正面向上的概率很大，但也仅有25%左右，造成试验结果和理论值不一致的原因，是试验十次数量太少，统计的规律性被试验的随机性掩盖了。

对于这个现象我们来考虑两家医院，大医院新生儿是45个，小医院是15个，问哪一家意愿新生男孩比例超过60%的天数多的可能性大？

答案是，小医院的概率更大一些。

因为根据中心极限定理，大样本的标准差比小样本的低得多。

Y1~B(45，0.5)，Y2~B(15，0.5)，超过60%，也就是说Y1超过27，而Y2超过9，

我们用python来计算

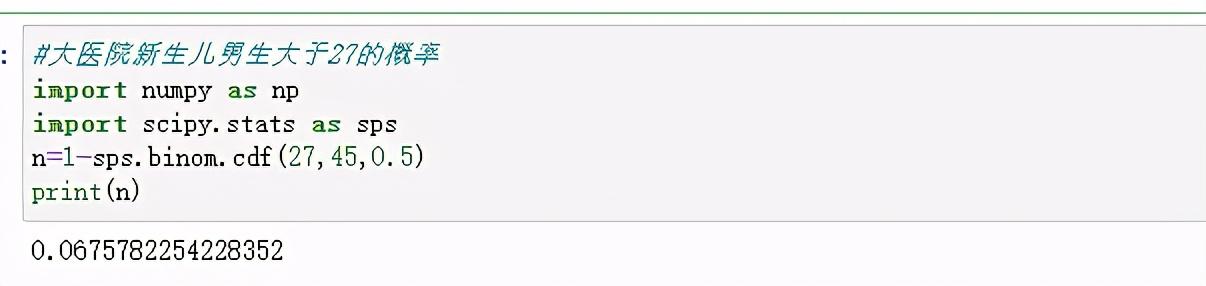
即大医院每日新生儿超过60%男孩的概率为6.7%，

即小医院每日新生儿超过60%男孩的概率为15%。

大样本比小样本更加稳定，因为当基数足够大的时候，每一个元素带来的影响都会被稀释掉，而当样本量较小时，每个样本的变化都会带来较大的波动。

贝叶斯概率的理解

假设一种疾病的检验方法，如果被传染，检验结果有99%为阳性，另一方面，未被传染的患者有2%的可能也呈现阳性，问一名患者被监测阳性，患病的概率为多少。

事件A：患者得病

事件B：检测结果呈阳性

P(A)=0.001，P(B|A)=0.99，P(B|~A)=0.02

P(A|B)=P(B|A)*P(A)/P(B)=P(B|A)*P(A)/(P(B|A)*P(B|~A)*P(~A))=0.99*0.001/(0.99*0.001+0.02*0.999)=4.72%

也就是说实际患病的概率5%.

Y以上，为学习所得，希望，对你有帮助。