定义

矩阵的奇异值分解（SVD）是指，将一个非零的 $m\times n$ 实矩阵 $A,A\in {\mathbf{R}}^{m\times n}$, 表示为三个实矩阵相乘的形式:
$$A=U\Sigma V^{\mathrm{T}}$$
其中，$U$ 是 $m$ 阶正交矩阵, $V$ 是 $n$ 阶正交矩阵，$\Sigma$ 是由降序排列的非负的对角线元素组成的 $m\times n$ 矩形对角矩阵, 满足

UUT=IVVT=IΣ=diag⁡(σ1,σ2,⋯ ,σp)σ1⩾σ2⩾⋯⩾σp⩾0p=min⁡(m,n)\begin{aligned} &U U^{\mathrm{T}}=I \\ &V V^{\mathrm{T}}=I \\ &\Sigma=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \cdots, \sigma_{p}\right) \\ &\sigma_{1} \geqslant \sigma_{2} \geqslant \cdots \geqslant \sigma_{p} \geqslant 0 \\ &p=\min (m, n) \end{aligned}​UUT=IVVT=IΣ=diag(σ1​,σ2​,⋯,σp​)σ1​⩾σ2​⩾⋯⩾σp​⩾0p=min(m,n)​

${\sigma }_i$成称为矩阵$A$的奇异值，$U$的列向量称为左奇异向量，$V$的列向量称为右奇异向量

ps：奇异值分解不要求矩阵$A$是方阵，矩阵的奇异值分解可以看作是方阵对角化的推广

常用形式

以上给出的奇异值分解又称为完全奇异值分解，实际常用的是奇异值分解的紧凑形式和截断形式。

设有$m\times n$ 实矩阵 $A$, 其秩为 $\mathrm{rank}(A)=r,r⩽\min (m,n)$:

紧奇异值分解:
$$A=U_r{\Sigma }_r{V}_r^{\mathrm{T}}$$

其中，$U_r$ 是 $m\times r$ 矩阵, $V_r$ 是 $n\times r$ 矩阵， ${\Sigma }_r$ 是 $r$ 阶对角矩阵；矩阵 $U_r$ 由完全奇异值分解中 $U$ 的前 $r$ 列、矩阵 $V_r$ 由 $V$ 的前 $r$ 列、矩阵${\Sigma }_r$ 由 $\Sigma$ 的前 $r$ 个对角线元素组成。紧奇异值分解的对角矩阵 ${\Sigma }_r$ 的秩与原始矩阵 $A$ 的秩相等。

截断奇异值分解：

$$A\approx U_k{\Sigma }_k{V}_k^{\mathrm{T}}$$

其中，$0<k<r$，$U_k$ 是 $m\times k$ 矩阵, $V_k$ 是 $n\times k$ 矩阵, ${\Sigma }_k$ 是 $k$ 阶对角矩阵; 矩阵 $U_k$ 由完全奇异值分解中 $U$ 的前 $k$ 列矩阵 $V_k$ 由 $V$ 的前 $k$ 列、矩阵 ${\Sigma }_k$ 由 $\Sigma$ 的前 $k$ 个对角线元素组成。对角矩阵${\Sigma }_k$的秩比原始矩阵$A$ 的秩低

性质

（1）设矩阵 $A$ 的奇异值分解为 $A=U\Sigma V^{\mathrm{T}}$, 则以下关系成立:
$$\begin{array}{rl}& A^{\mathrm{T}}A={\left(U\Sigma V^{\mathrm{T}}\right)}^{\mathrm{T}}\left(U\Sigma V^{\mathrm{T}}\right)=V\left({\Sigma }^{\mathrm{T}}\Sigma \right)V^{\mathrm{T}}\\ & A{A}^{\mathrm{T}}=\left(U\Sigma V^{\mathrm{T}}\right){\left(U\Sigma V^{\mathrm{T}}\right)}^{\mathrm{T}}=U\left(\Sigma {\Sigma }^{\mathrm{T}}\right)U^{\mathrm{T}}\end{array}$$

（2）矩阵$A$的奇异值分解中，左奇异向量，右奇异向量和奇异值存在一一对应的关系

（3）矩阵 $A$ 的奇异值分解中，奇异值 ${\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n$ 是唯一的，而矩阵 $U$ 和 $V$ 不 是唯一的。

（4）矩阵 $A$ 和 $\Sigma$ 的秩相等, 等于正奇异值 ${\sigma }_i$ 的个数 $r($ 包含重复的奇异值，奇异值都是非负的)

（5）矩阵 $A$ 的 $r$ 个右奇异向量 $v_1,v_2,\cdots ,v_r$ 构成 $A^{\mathrm{T}}$ 的值域 $R\left(A^{\mathrm{T}}\right)$ 的一组标准正交基

几何解释

从线性变换的角度理解奇异值分解:

$m\times n$ 矩阵$A$ 表示从 $n$ 维空间 ${\mathbf{R}}^n$ 到 $m$ 维 空间 ${\mathbf{R}}^m$ 的一个线性变换，
$$T:x\to Ax$$
$x\in {\mathbf{R}}^n,Ax\in {\mathbf{R}}^m,x$ 和 $Ax$ 分别是各自空间的向量。

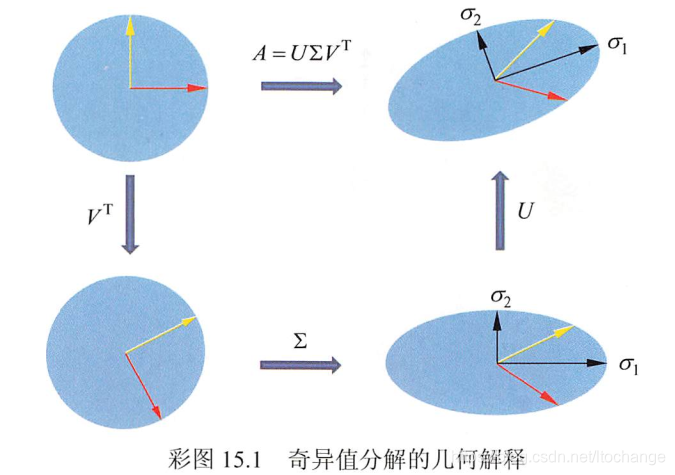
$A=U\Sigma V^{\mathrm{T}}$ 奇异值分解可以看作, 将线性变换$A$转换为三个简单变换. 例如下图, 给出了原始空间的标准正交基 (红色与黄色)，经过坐标系的旋转变换 $V^{\mathrm{T}}$ 、坐标轴的缩放变换 $\Sigma$, 坐标系的旋转变换 $U$ ，得到和经过线性变换 $A$ 等价的结果。