数学建模matlab实现灰色预测
需要注意的是,灰色系统预测在预测过程中对数据序列的样本量要求相对较低,但也容易受到数据质量和数据特征的影响。因此,在应用灰色系统预测时,需要合理处理数据、选择适当的灰色发展模型,并结合实际情况对预测结果进行分析和评估。灰色系统预测(Grey System Forecasting)是一种基于灰色理论的预测方法,适用于数据样本较少、信息不完全或者缺乏足够的先验知识的情况。预测与评估:基于建立的灰色发展
1.基本概念
灰色系统预测(Grey System Forecasting)是一种基于灰色理论的预测方法,适用于数据样本较少、信息不完全或者缺乏足够的先验知识的情况。它通过对系统中的数据进行灰色建模和分析,进行未来趋势的预测。
灰色系统预测主要包括以下几个步骤:
-
数据序列建模:首先,根据已有的数据序列,将其转化为灰色数据序列。通常采用生成级比序列、累加生成序列等方法,将原始数据序列转化为灰色级数。
-
确定发展模型:根据灰色级数序列的特点,选择合适的发展模型。常用的模型包括灰色一阶模型(GM(1,1))、灰色二阶模型(GM(2,1))等。每个模型都有其独特的发展规律和特征。
-
模型参数估计:通过灰色发展模型,估计模型的参数。这些参数用于描述数据序列的发展规律和趋势。参数的估计可以使用最小二乘法、最小偏差法等统计方法进行。
-
模型检验:对估计得到的模型进行检验,评估其预测精度和可靠性。常用的检验方法包括残差检验、相对误差检验等。
-
预测与评估:基于建立的灰色发展模型,进行未来趋势的预测。根据模型的预测结果和可靠性评估,得出对未来趋势的预测和判断。
需要注意的是,灰色系统预测在预测过程中对数据序列的样本量要求相对较低,但也容易受到数据质量和数据特征的影响。因此,在应用灰色系统预测时,需要合理处理数据、选择适当的灰色发展模型,并结合实际情况对预测结果进行分析和评估。同时,为了提高预测精度,可以结合其他预测方法和技术进行综合预测。
2.代码实现
| 年份 | 国内生产总值(亿元) | 年份 | 国内生产总值(亿元) |
| 2013 | 588141.2 | 2018 | 915243.5 |
| 2014 | 644380.2 | 2019 | 983751.2 |
| 2015 | 685571.2 | 2020 | 1005451.3 |
| 2016 | 742694.1 | 2021 | 1141230.8 |
| 2017 | 830945.7 | 2022 | 1197250.4 |
clc,clear;
syms a b;
c=[a b]';
A=[588141.2 644380.2 685571.2 742694.1 830945.7 915243.5 983751.2 1005451.3 1141230.8 1197250.4];
B=cumsum(A); %原始数据累加
n=length(A);
for i=1:(n-1)
C(i)=(B(i)+B(i+1))/2; %生成累加矩阵
end
%计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
%预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10) %只推测后10个数据,可以从此修改
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end
G=[];G(1)=A(1);
for i=2:(n+10) %只推测后10个数据,可以从此修改
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=2013:2022;
t2=2013:2032; %多10组数据
h=plot(t1,A,'o',t2,G,'-'); %原始数据与预测数据的比较
set(h,'LineWidth',1.5);
xlabel('年份');
ylabel('国内生产总值(亿元)');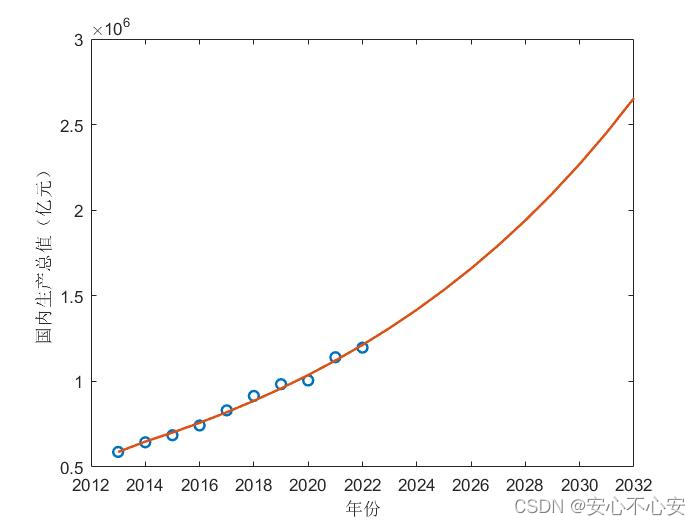

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容








所有评论(0)