第一部分 邮递员问题

一. 问题引入

        中国邮递员问题（Chinese Postman Problem, CPP）是图论中的一个著名问题，它是在1960年由我国学者管梅谷首先提出并研究的。简单来说，就是问：一个邮递员从邮局出发，把一个城市的所有街道都至少走一遍，最后回到邮局，问怎样使他走的总路程最小？这个问题有许多现实的应用，比如一个除雪车从城市的某一位置出发，把城市里所有街道的雪都清扫了，再回到出发点，问怎么走路程最少。我们可以把城市看作一个连通的、简单的带权无向图，节点代表街道的交叉，边代表街道，其权重是街道的长度。一个回路（circuit）是从某一点出发回到这一点的路径，并且可以将一条边经过多次。所以，中国邮递员问题就是求无向图上权重最小（即最短）的回路。
                        
        原文链接：https://blog.csdn.net/qaqwqaqwq/article/details/129919124

翻译成另一语境的问题：

        我的朋友阿莱克修斯是一名lovelive虹咲学院死忠粉，由于他第一次到日本想要进行圣地巡礼（顺便买谷子），他需要把每条路都走一遍。请问他应该如何选择路线？

（已获得原作者许可）

二. 模型简化

     用wps画出如下模型：

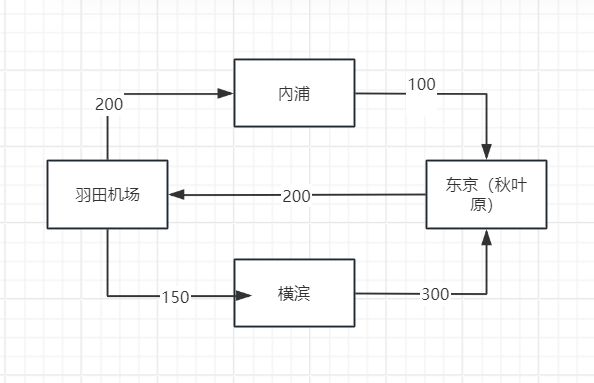
（距离仅供参考【懒得查。。。】）

三. 解题思路

        为了解决这个问题让我们先了解一些概念：

节点：每个位置，如以上方框中显示的；

度数：节点周围的通路；

权重：距离，时间等决定分配的要素；

奇节点：奇度数的节点（如羽田机场和东京）；

偶节点：偶度数的节点；

        知道概念了，让我们上工具：Edmonds-Johnson 算法

        握手引理（Handshaking Lemma）提到：无向图中所有节点的度数之和等于边数乘2，那么度数之和和一定是偶数。而只有偶数个奇数之和才能是偶数，所以奇节点一定有偶数个。

        也就是说，你想走完每一条路，你进去一次节点就必须出一次节点，如最最简单的模型：宿舍—>教室——>宿舍，你出了一次宿舍，入了一次宿舍，入了一次教室，出了一次教室。那么我们可以说，如果图中全为偶节点，那么通过进和出正好能全部走完。

        but，如果有奇节点怎么办，很简单，补一个度数就行，没补一个度数相当于你在现实中重复走了同一条路一次。例如以上的羽田机场就是一个度数为三的奇节点，我们可以在中间再补一个度数（也就是再走200km的路便可完成循环，即羽—>内—>东—>羽—>东—>横—>羽）使其变为偶节点，此时恰巧是走的最短的路径。

        但是，只要补成偶节点了就一定是最短路径了么？很明显不是。

        让我们看看下面这张图：

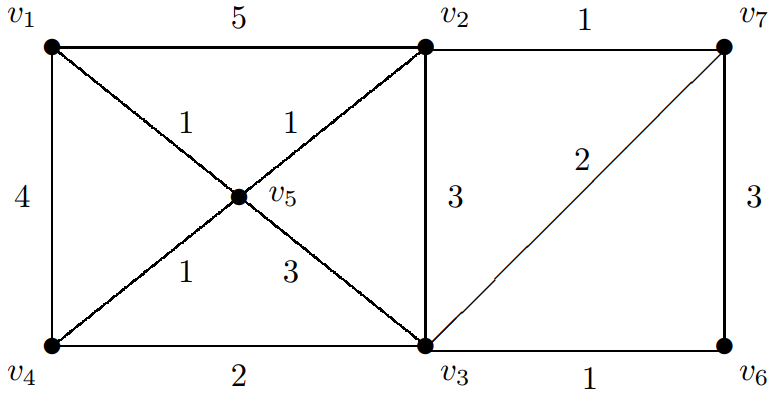
        先找出奇节点：v1（3度），v4（3度），v3（5度），v7（3度）。

        然后开始连线，记住如果两节点中间还有节点，那么就要把中间结点也连上，我随意将两对奇节点相连（v1 v3）和（v2 v4）。

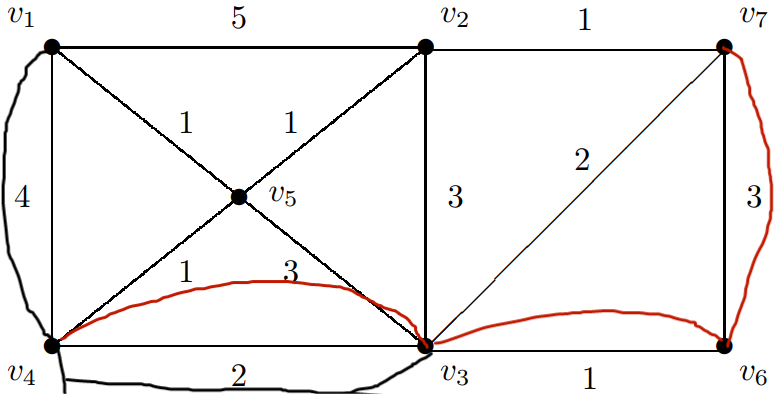
（其中红笔为v4到v7，黑笔为v1到v3）

        我们可以发现v4到v3这条线上有了红黑两线，很明显重复了，我们可以把红黑两线删掉。

        我们又可以发现，从v1直接到v4没有从v1到v5再到v4近，所以将黑线转移至v1到v5和v5到v4上。同时v3直接到v7是最近的，我们可以将两个红线删掉，在v3和v7间添上红线，如下图所示：

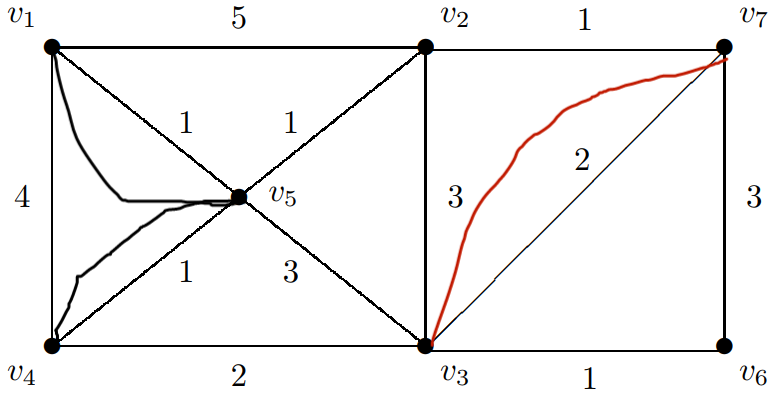  此时所有节点全为偶节点（读者可自行验证其能否一笔画完）。

思路来自：图论 中国邮递员问题 奇偶点图上作业法求最优环游_哔哩哔哩_bilibili

补：

对以下ppt进行解释：

1. 总度数为节点的两倍，即“一进一出”原则

2. 由于总度数为偶数，无论奇数个还是偶数个偶节点的度数都是偶数个，两者一减便可知奇节点数量应为偶数个（如羽和东，或另一个图的四个奇节点）

3.一个节点“一进一出”（正进负出）

四. 应用

例一：人狼羊菜渡河问题

1.问题描述

2.解法

3.代码实现
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
 
int ways[4] = { 8, 12, 10, 9 }; 
// 二进制分别是1000, 1100, 1010, 1001, 对应题目要求的四种过河方式
int state, ending, go_left, start_drct, end_drct, has_answer;
string items = "CGWM";
vector<int> ans;
 
void explain(vector<int> ans){  // 对ans中的整数作解释输出
    if(has_answer) cout << "\n";
    has_answer = 1;
    int tmp = go_left;
    for(auto step : ans){
        for(int i = 3; i >= 0; i--){
            if(step & (1 << i)) cout << ".";
            else cout << items[i];
        }
        if(go_left) cout << " <- ";
        else cout << " -> ";
        go_left = !go_left;
        for(int i = 3; i >= 0; i--){
            if(step & (1 << i)) cout << items[i];
            else cout << ".";
        }
        cout << "\n";
    }
    go_left = tmp;
}
 
void DFS(int last)  // last传递上次的过河方式
{
    if (state == 3 || state == 6 || state == 7 || state == 8 || state == 9 || state == 12)   // 0011, 0110, 0111, 1000, 1001, 1100, 对应6种狼和羊独处，羊和菜独处的情况
        return;
    
    if (state == ending && (ans.size() & 1) == (start_drct == end_drct)) {
        // 验证当前状态是否和结束状态相同的同时通过答案的个数检查箭头是否匹配
        explain(ans);
        return;
    }
 
    for (int i = 0; i < 4; i++) {
        if(i == last) continue;  
        // 如果当前的过河方式和上次相同, 则又回到了上次过河前的状态，所以跳过本轮循环
        state = state ^ ways[i];  //通过异或运算实现过河方式的模拟
        if(find(ans.begin(), ans.end(), state) == ans.end()){
            ans.push_back(state);
            DFS(i);
            ans.pop_back();
        }
        state = state ^ ways[i];  // 再做一次异或运算回溯到过河前的状态
    }
}
 
int main()
{
    string str;
    getline(cin, str);
    for (int i = 0; i < 4; i++) {
        if (str[i] == '.')
            state = state | (1 << (3 - i));
    }
    if(str[5] == '<') {
        start_drct = 1;
        go_left = !go_left;
    }
    getline(cin, str);
    for (int i = 0; i < 4; i++) {
        if (str[i] == '.')
            ending = ending | (1 << (3 - i));
    }
    if(str[5] == '<') end_drct = 1;
    ans.push_back(state);
    if(state != ending) DFS(-1);  
    // -1为随便取的一个负值, 这是因为第一次过河没有“上一次的过河方式”, 所以随便取一个负值保证每种方法都不会被跳过
    if(!has_answer) cout << "None";
    return 0;
}
4.总结：有限制的一笔画问题

代码来源：作业笔记：（PTA） 人狼羊菜过河-CSDN博客

例二：渡河问题

1. 问题描述

2. 解法

3. 小思考

用第一部分的邮递员模型能快速求出最短用的步数，方法如下：

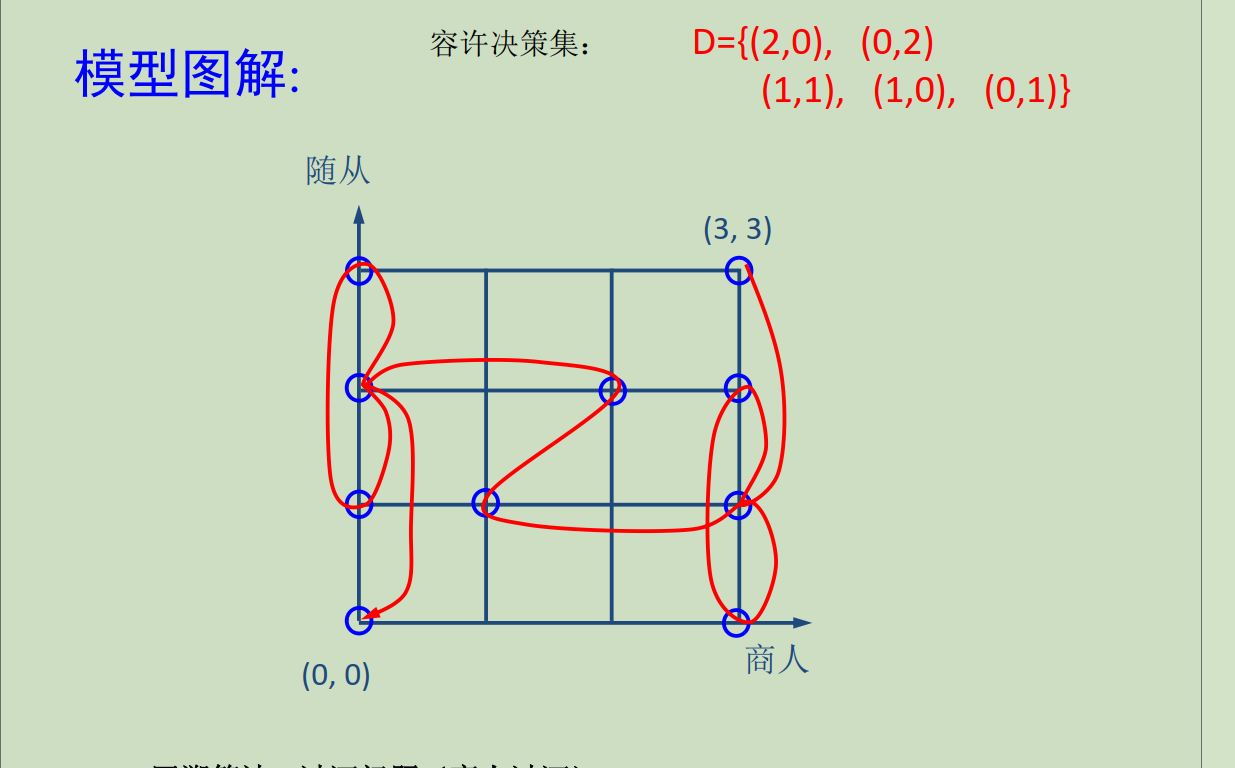
（1）由题意易得出在此岸的随从商人模型，如上图（无连线状态）

（2）由于渡河人数可为1或2，所以总路径节点图为

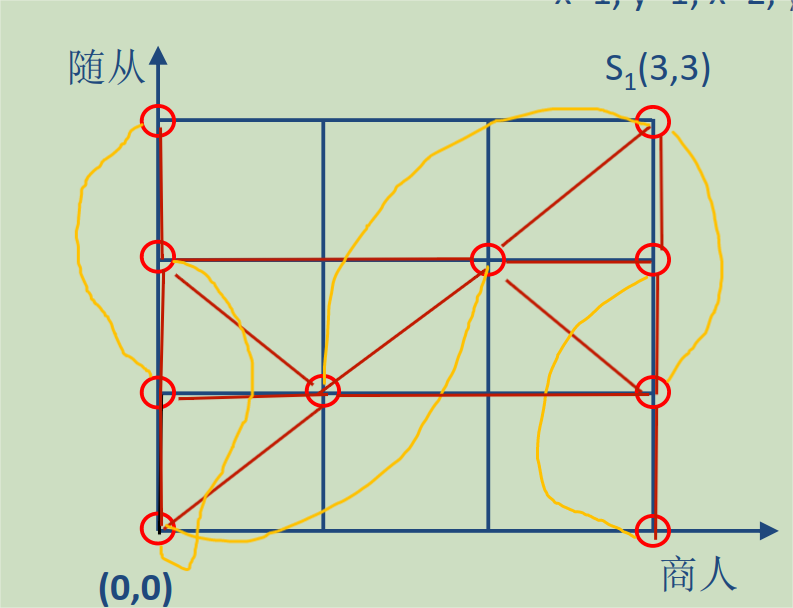
（3）其中（3,1）和（0,2）为奇节点，由于每条边的长为1，最短连接后的图为

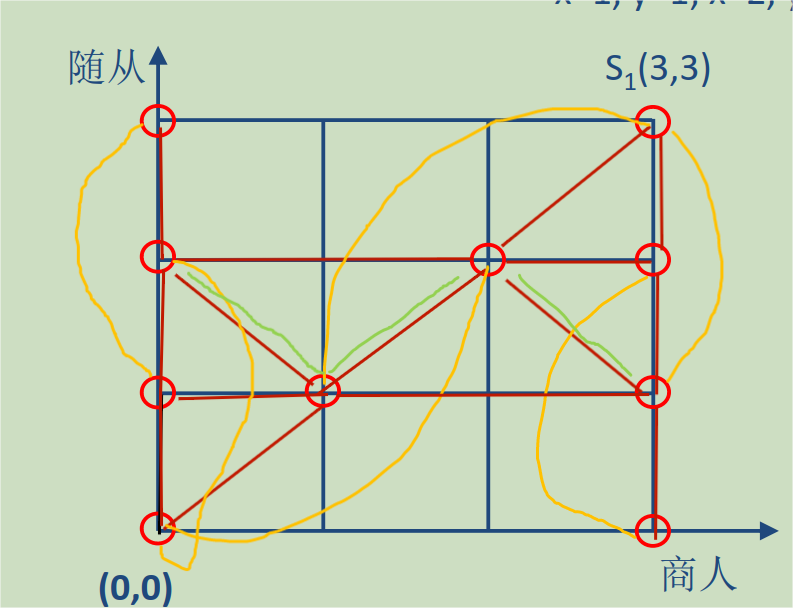
（4）数出总共有22条线，由于是一来一回，从（3,3）到（0,0）的单程最短应为11条，也就是最少运 11次

4. 代码实现

　using namespace std;
　bool matrix[4][4],turn;
　int record[128][2],pos=1;
　bool check[128];
　　/*判断这一状态是否在前面已经出现过*/
　　bool isRepeat(int x,int y,bool turn)
　　{
　　 for(int i=0;i<POS;I++)
　　 if(x==record[i][0]&&y==record[i][1]&&turn==check[i])
　　 return true;
　　 return false;
　　}
　　void search(int px,int py)
　　{
　　 static int goStep[5][2]={{0,2},{1,1},{2,0},{0,1},{1,0}};
　　 int i;
　　 if(px==0&&py==0)
　　 {
　　 for(i=0;i<POS;I++)
　　 {
　　 cout<<"("<<RECORD[I][0]<<","<<RECORD[I][1]<<
　　 ")<==>("<<3-record[i][0]<<","<<3-record[i][1]<<")"<<ENDL;
　　 }
　　 system("pause");
　　 }
　　 else if(turn==false)
　　 {
　　 for(i=0;i<5;i++)
　　 {
　　 px-=goStep[i][0];
　　 py-=goStep[i][1];
　　 if(px<0||px>3||py<0||py>3||matrix[px][py]||isRepeat(px,py,turn))
　　 {
　　 px+=goStep[i][0];
　　 py+=goStep[i][1];
　　 continue;
　　 }
　　 record[pos][0]=px,record[pos][1]=py;
　　 check[pos]=turn;
　　 pos++;
　　 turn=(turn==true?false:true);
　　 search(px,py);
　　 pos--;
　　 turn=(turn==true?false:true);
　　 px+=goStep[i][0];
　　 py+=goStep[i][1];
　　 }
　　 }
　　 else
　　 {
　　 for(i=0;i<5;i++)
　　 {
　　 px+=goStep[i][0];
　　 py+=goStep[i][1];
　　 if(px<0||px>3||py<0||py>3||matrix[px][py]||isRepeat(px,py,turn))
　　 {
　　 px-=goStep[i][0];
　　 py-=goStep[i][1];
　　 continue;
　　 }
　　 record[pos][0]=px,record[pos][1]=py;
　　 check[pos]=turn;
　　 pos++;
　　 turn=(turn==true?false:true);
　　 search(px,py);
　　 pos--;
　　 turn=(turn==true?false:true);
　　 px-=goStep[i][0];
　　 py-=goStep[i][1];
　　 }
　　 }
　　}
　　int main()
　　{
　　 int px=3,py=3;
　　 for(int i=0;i<4;i++)
　　 for(int j=0;j<4;j++)
　　 {
　　 if(i==j||i==0||i==3);
　　 else matrix[i][j]=true;
　　 }
　　 record[0][0]=record[0][1]=3;
　　 check[0]=true;
　　 search(px,py);
　　 return 0;
　　}
5. 总结：多步决策下的一笔画最短路径问题

代码来源：回溯算法---过河问题（商人过河）_商人过河问题。有几种解法-CSDN博客

第二部分 最优截断切割问题

一. 问题描述

        从一个长方体中加工出一个已知尺寸、位置预定的长方体（这两个长方体的对应表面是平行的），通常要经过6 次截断切割.设水平切割单位面积的费用是垂直切割单位面积费用的r倍.且当先后两次垂直切割的平面（不管它们之间是否穿插水平切割）不平行时，因调整刀具需额外费用e.试设计一种安排各面加工次序（称“切割方式”）的方法，使加工费用最少.

二. 假设

1. 水平切割单位面积费用为r，垂直切割单位面积费用1；

2.先后两次切割平面不平行时，调整刀具需额外费用e；

3.第一次切割前，刀具已调整完毕，即第一次垂直切割不加入刀具调整费用；

4.每个待加工长方体必须经6次截断切割.

三. 模型建立

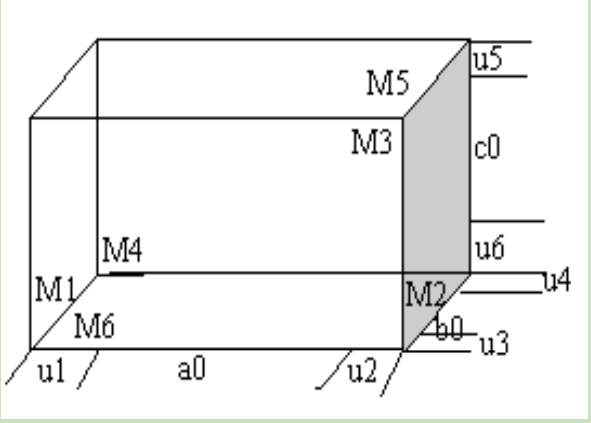
首先有请D指导给出正常解法：

问题分析

  1. 切割类型：

    • 垂直切割：分为两个方向（如x和y方向），单位面积费用为1。

    • 水平切割（如z方向），单位面积费用为垂直切割的rr倍。

  2. 调整费用：若连续两次垂直切割方向不同（如x→y），需支付额外费用e，无论中间是否穿插水平切割。

关键策略

  1. 最小化调整费用：

    • 连续完成同一方向的垂直切割，将方向切换次数降至1次（仅需支付一次e）。

  2. 最小化切割面积费用：

    • 先切割面积较大的垂直方向，减少后续切割面积。

    • 最后处理水平切割，利用已缩减的尺寸降低费用。

具体步骤

  1. 确定垂直切割顺序：

    • 计算两种垂直切割顺序的总费用：

      • 顺序1（先x后y）：总费用为 2YZ+2xZ。

      • 顺序2（先y后x）：总费用为 2XZ+2yZ。

    • 选择费用更小的顺序。

  2. 安排水平切割：

    • 将两次水平切割置于所有垂直切割之后，此时水平切割面积为x×y，费用为 2rxy。

  3. 总费用计算：

    总费用=min⁡(2YZ+2xZ, 2XZ+2yZ)+2rxy+e

示例说明

假设原长方体尺寸为 X×Y×Z，需加工内部长方体尺寸为 x×y×z：

  • 若 2YZ+2xZ<2XZ+2yZ：

    • 按顺序切割：x方向两次 → y方向两次 → z方向两次。

    • 调整费用 e=1，水平切割费用 2rxy。

  • 反之，优先切割y方向。

        总结下来，就是先切大截面，再切更小的那面，最后换方向切最后一面。大中切大平面，中中切中平面，小中切小平面。

        用图论的方法即是从（0,0,0，none【未切状态】）到（2,2,2，*【已切状态】），每走一步加上权重，再做比较。

        

第三部分 最短路径问题

一. 算法介绍

而为了了解图论的思想，我们先要了解以下算法：

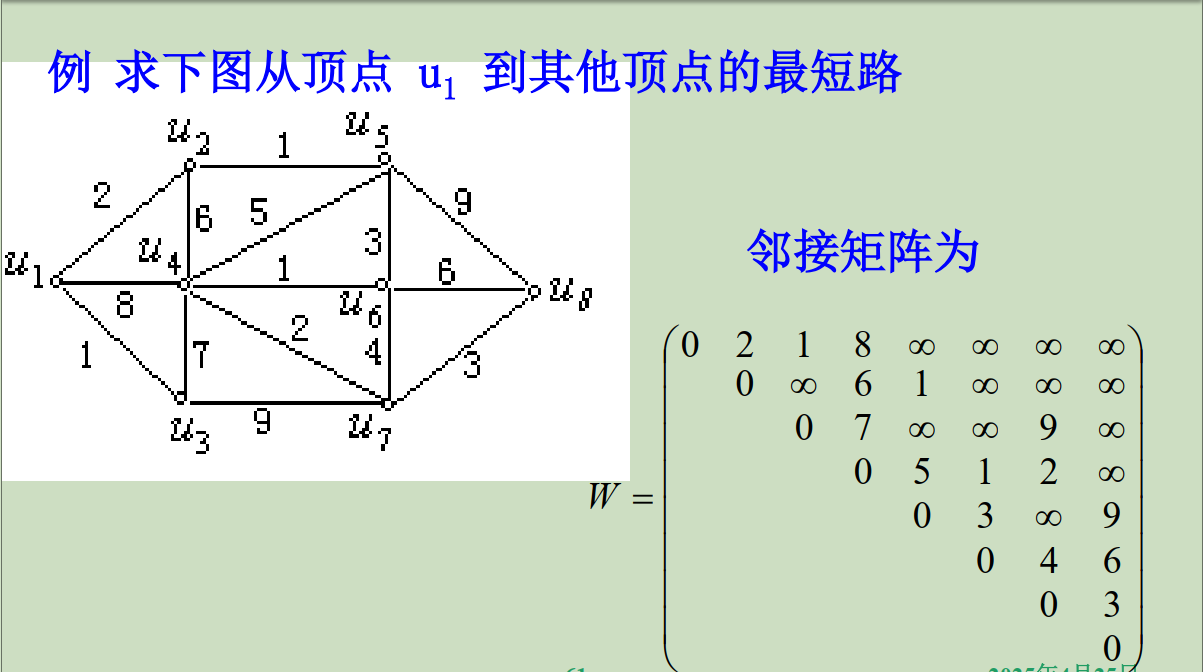
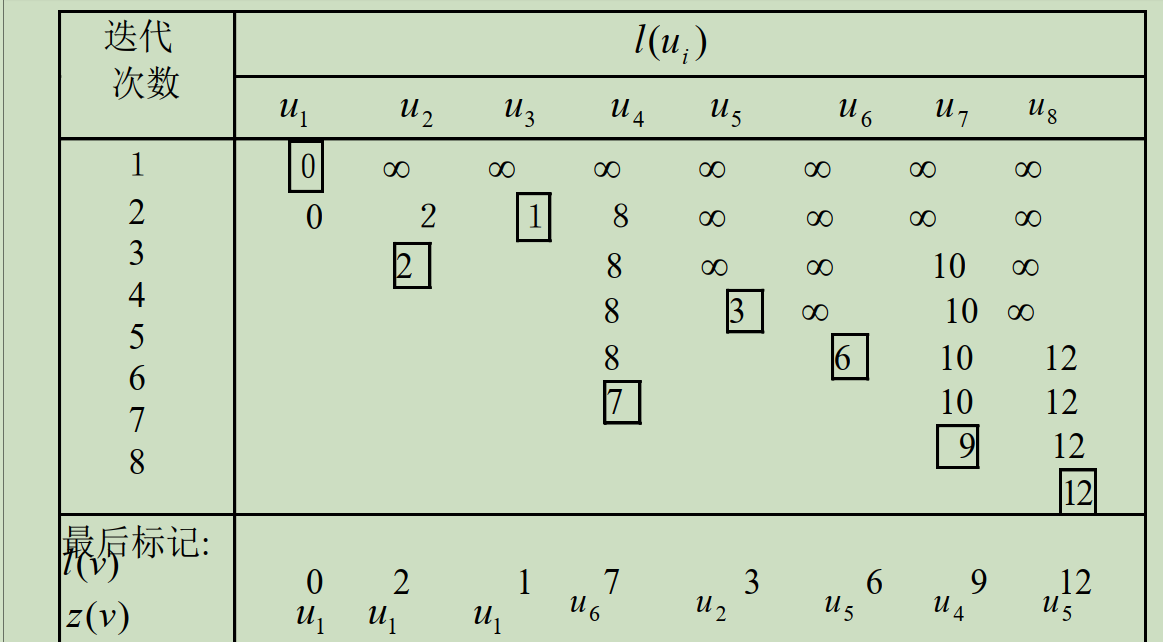
1. Dijkstra算法

  • 迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

算法实现：图-最短路径-Dijkstra(迪杰斯特拉)算法_哔哩哔哩_bilibili

        具体可看该视频；

      邻接矩阵 ：

        邻接矩阵用于描述图上顶点间的关系。例如临接矩阵D [ i ] [ j ]表示顶点 i 到顶点 j 的直达距离，可将其赋值为无穷大 Inf 来表示顶点 i 无法直达到顶点 j 。（该图右下角【竖着看】）

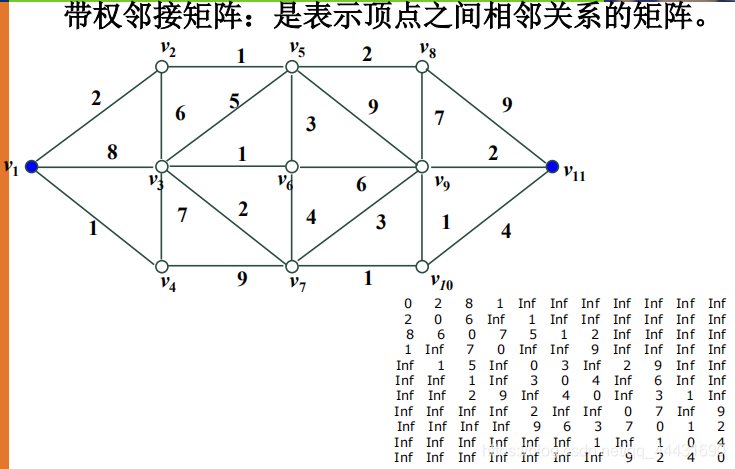
做法：首先写出邻接矩阵，然后每一点迭代一次，第一行第一个数加上第一行所有值为v1对所有点的最小值的第一次迭代值，第一行第二个数加上第二行的所有值为v1对所有点的最小值的第二次迭代值以此类推，再找出最小值点作为v1到所有点的最近值。把取最小值的点记作z（v），根据重要性质（在后面）可以推出每一点的最短路径。

        代码实现： 

 来源于：图论：Dijkstra算法——最详细的分析，图文并茂，一次看懂！-CSDN博客

% 文件命名为：tulun1.m
weight=    [0     2     8     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf;
            2     0     6   Inf     1   Inf   Inf   Inf   Inf   Inf   Inf;
            8     6     0     7     5     1     2   Inf   Inf   Inf   Inf;
            1   Inf     7     0   Inf   Inf     9   Inf   Inf   Inf   Inf;
          Inf     1     5   Inf     0     3   Inf     2     9   Inf   Inf;
          Inf   Inf     1   Inf     3     0     4   Inf     6   Inf   Inf;
          Inf   Inf     2     9   Inf     4     0   Inf     3     1   Inf;
          Inf   Inf   Inf   Inf     2   Inf   Inf     0     7   Inf     9;
          Inf   Inf   Inf   Inf     9     6     3     7     0     1     2;
          Inf   Inf   Inf   Inf   Inf   Inf     1   Inf     1     0     4;
          Inf   Inf   Inf   Inf   Inf   Inf   Inf     9     2     4     0;];
[dis, path]=dijkstra(weight,1, 11)
function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
    if i~=start
        label(i)=inf;
    end
end
s(1)=start; u=start;
while length(s)<n
    for i=1:n
        ins=0;
        for j=1:length(s)
            if i==s(j)
                ins=1;
            end
        end
        if ins==0
            v=i;
            if label(v)>(label(u)+w(u,v))
                label(v)=(label(u)+w(u,v));
                f(v)=u;
            end
        end
    end
    v1=0;
    k=inf;
    for i=1:n
        ins=0;
        for j=1:length(s)
            if i==s(j)
                ins=1;
            end
        end
        if ins==0
            v=i;
            if k>label(v)
                k=label(v);  v1=v;
            end
        end
    end
    s(length(s)+1)=v1;
    u=v1;
end
min=label(terminal); path(1)=terminal;
i=1;
while path(i)~=start
    path(i+1)=f(path(i));
    i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

得到最小路径后，应注意以下性质：

注：要注意路径是单向的还是多向的。

另：实战应用论文数学建模十大经典算法之图论算法实战应用论文 - 道客巴巴

2. floyd算法

视频参考：图-最短路径-Floyd(弗洛伊德)算法_哔哩哔哩_bilibili

核心思路：通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

算法过程：

  • 从任意一条单边路径开始。左右两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。

  • 对于每一对顶点u和v，看是否存在一个顶点w使得从u到w再到v比已知的路径更短，如果更短，则更新它。

解释：和dijkstra算法一样，先写出临接矩阵，再通过固定中间点进行数据迭代，如以下题目

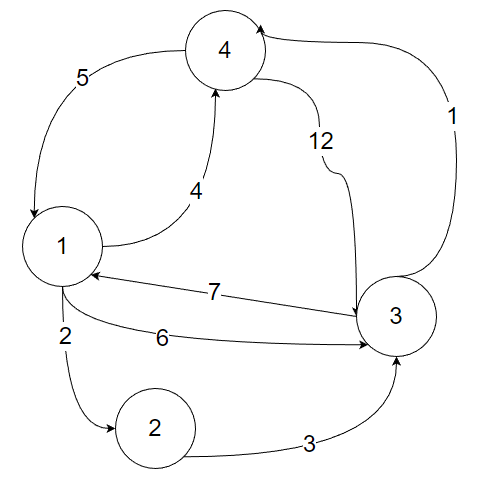
        有4个点，临接矩阵如下（注：由于往返的权值不一样，需要补全）

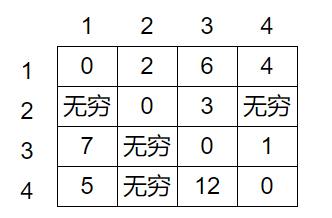
        接下来先定好第一行与第一列不变（即以1为中间点，其余所有点都要经过它但他到所有点的距离都不变），斜边x=-y不变（自己到自己的距离恒为零【自己吓自己（雾】），对其余所有点进行验证，方法为：if(e[i][j]>e[i][1]+e[1][j]){ e[i][j]=e[i][1]+e[1][j];（即若从i行到j行的距离大于从i行到1再从1到j的距离，那么就更新该距离），迭代一次后，固定第二行与第二列不变，x=-y斜边不变，对其余所有点进行验证，方法为：

for (int i = 1; i <=N ; i++) {
    for (int j = 1; j <=N; j++) {
        if(e[i][j]>e[i][2]+e[2][j]){
            e[i][j]=e[i][2]+e[2][j];
        }
    }（注，第一行与第一列的数也进行了迭代）后面同理，直到全部迭代完为止。

        b站视频还给出了定前一个的点的方法，其实按照该方法先画出前一点的矩阵图（不相邻写-1），在迭代时若e[i][j]更改，该矩阵图相应点的值改为前一次记录的现中间点与该点的值。

二. 例题

例一：

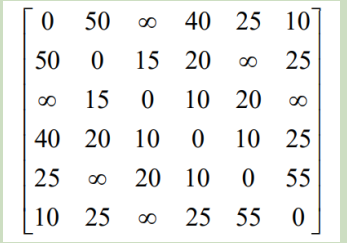
算法实例：

n = 6
INFINITY = float('inf')  
D = [
    [0, 50, INFINITY, 40, 25, 10],
    [50, 0, 15, 20, INFINITY, 25],
    [INFINITY, 15, 0, 10, 20, INFINITY],
    [40, 20, 10, 0, 10, 25],
    [25, INFINITY, 20, 10, 0, 55],
    [10, 25, INFINITY, 25, 55, 0]
]
P = [[0] * n for _ in range(n)]  # 使用列表生成式避免共享行

# 初始化路径矩阵
for u in range(n):
    for v in range(n):
        if D[u][v] != INFINITY and u != v:
            P[u][v] = u
        else:
            P[u][v] = -1  # 不可达时标记为-1

print("初始状态：")
print("距离矩阵为:")
for row in D:
    print(row)
print("路径矩阵为:")
for row in P:
    print(row)

# Floyd算法核心
for w in range(n):
    for u in range(n):
        for v in range(n):
            if D[u][w] + D[w][v] < D[u][v]:
                D[u][v] = D[u][w] + D[w][v]
                P[u][v] = P[w][v]

print("最终结果：")
print("距离矩阵为:")
for row in D:
    print(row)
print("路径矩阵为:")
for row in P:
    print(row)

代码参考：【Floyd最短路径算法】--python实现_floyd算法python代码-CSDN博客

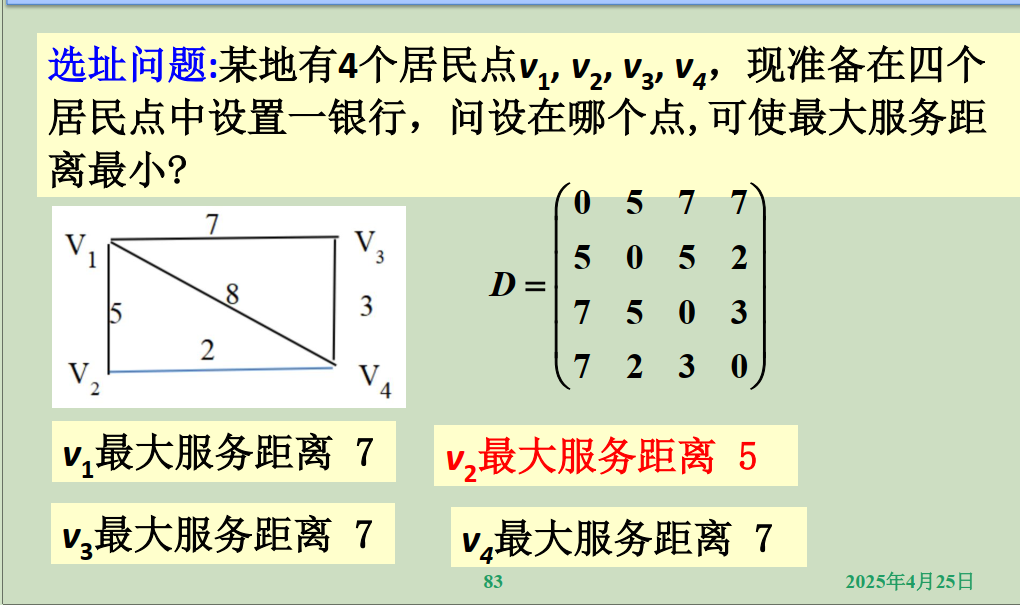
例二：

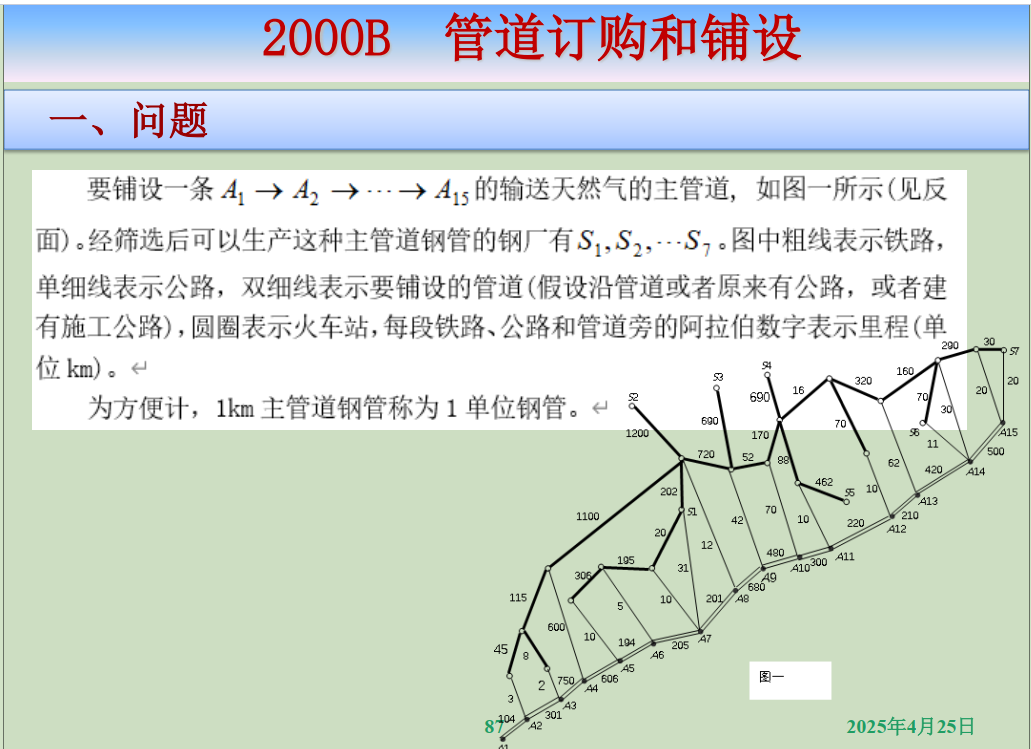
第四部分 相关竞赛题

---------------------------------------------------------------------------------------------------------------------------------

（完！！！！）

--------------------------------------------------------------------------------------------------------------------------------

（未经许可禁止搬运）

# 图论
Logo
DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

cover

KingbaseES数据库：医疗信创潮涌沅江，国产化信创打造医疗新质生产力

avatar DAMO开发者矩阵
cover

告别迁移焦虑：金仓KDMS V4带你轻松搞定数据库国产化替代

avatar DAMO开发者矩阵
cover

KingbaseES数据库在常德二院全栈国产化信创中产生新质生产力,医疗信创的部署如何实现，如何操作？

avatar DAMO开发者矩阵