1 主成分分析

主成分分析（PCA）是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息。一般而言，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可以考虑使用主成分分析的方法来对数据进行简化。

<1>问题的提出

在实际问题研究中，多变量问题是经常遇到的。变量太多，无疑会增加分析问题的难度和复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映地信息。
主成分分析方法就是处理这种问题的一种工具。它是把原来多个变量划分为少数几个综合指标的一种统计分析方法。从数学角度看，它是一种降维处理技术。

<2>数据降维的作用

降维是将高维度的数据（指标太多）保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。其优点有：

• 使得数据集更易使用
• 降低算法的计算开销
• 去除噪声
• 使得结果容易理解

举个例子：

<3>主成分分析的思想

假设有$n$个样本，$p$个指标，则可构成大小为$n\times p$的样本矩阵$x$：

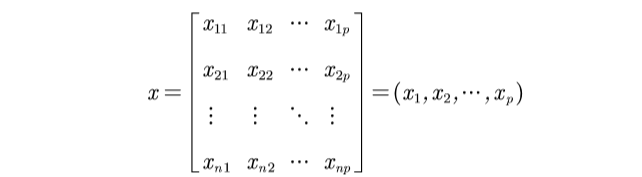
为了降维，我们想找到新的一组变量$z_1,z_2,...,z_m(m\le p)$，它们满足：

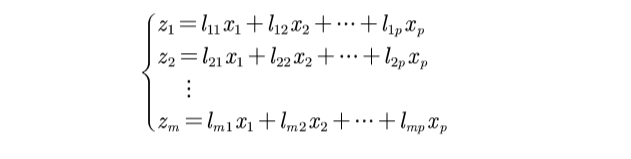
系数$l_{ij}$的确定原则：

• $z_i$与$z_j(i\ne j；i,j=1,2,...,m)相互无关；$
• $z_1$是$x_1,x_2,...,x_p$的一切线性组合中方差最大者；
• $z_2$是与$z_1$互不相关的$x_1,x_2,...x_p$的所有线性组合中方差最大者；
• 以此类推，$z_m$是$z_1,z_2,...,z_{m-1}$不相关的$x_1,x_2,...x_p$的所有线性组合中方差最大者。
• 新变量指标$z_1,z_2,...,z_m$分别称为原变量指标$x_1,x_2,...x_p$的第一，第二…第m主成分。

<4>PCA的计算步骤

假设有$n$个样本，p个指标，则可构成大小为$n\times p$的样本矩阵$x$：

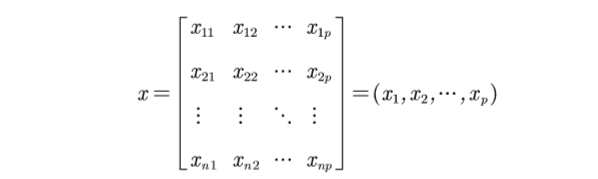
• 1> 首先对其进行标准化处理：
  

• 2> 计算标准化样本的协方差矩阵：

• 3>计算R的特征值和特征向量：

• 4>计算主成分贡献率以及累计贡献率：
  

• 5> 写出主成分
  一般取累计贡献率超过80%的特征值所对应的第一、第二、…、第m（$m\le p$）个主成分。第i个主成分：$F_i=a_{1i}{X}_1+a_{2i}{X}_2+...+a_{pi}{X}_p(i=1,2,...,m)$

• 6> 根据系数分析主成分代表的意义

• 对于某个主成分而言，指标前面的系数越大，代表该指标对于该主成分的影响越大。

• 7> 利用主成分分析的结果进行后续分析
  可用于聚类分析（方便画图）；回归分析；不可用于评价模型。

<5>应用例子：

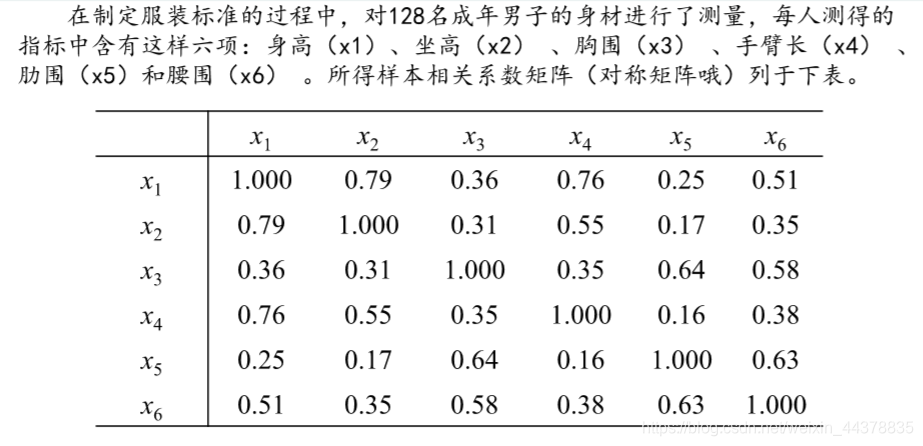
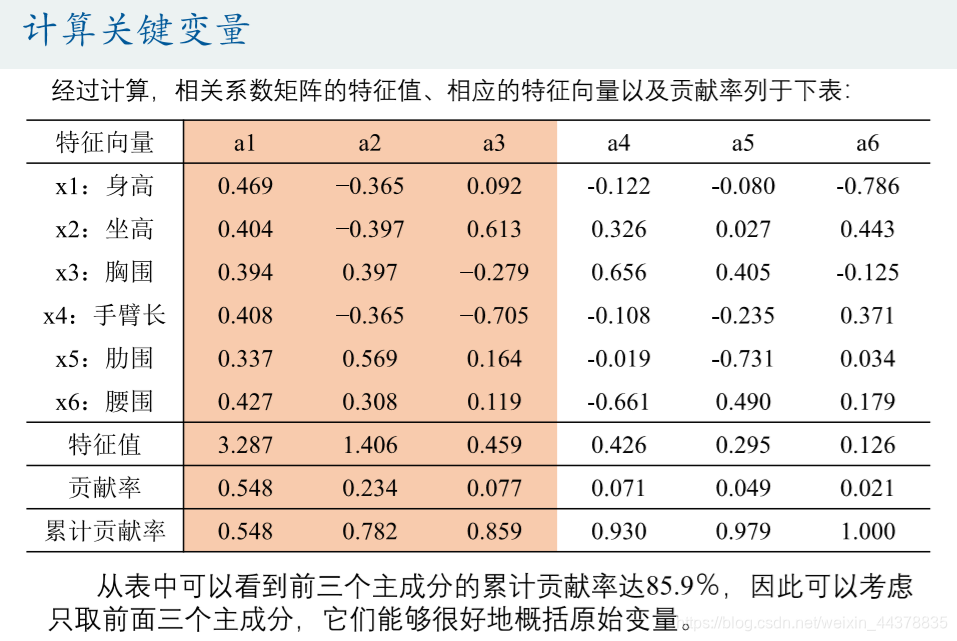
参考：清风数学建模