分析dmp文件使用表空间_R语言使用贝叶斯层次模型进行空间数据分析
原文链接:http://tecdat.cn/?p=10932tecdat.cn介绍在本节中,我将重点介绍使用集成嵌套 拉普拉斯近似方法的贝叶斯推理。 可以 估计贝叶斯 层次模型的后边缘分布。 鉴于模型类型非常广泛,我们将重点关注用于分析晶格数据的空间模型。数据集:纽约州北部的白血病为了说明如何与空间模型拟合,将使用纽约白血病数据集。该数据集记录了普查区纽约州北部的许多白血病病例。数据集中的一些变
原文链接:
http://tecdat.cn/?p=10932tecdat.cn介绍
在本节中,我将重点介绍使用集成嵌套 拉普拉斯近似方法的贝叶斯推理。
可以 估计贝叶斯 层次模型的后边缘分布。 鉴于模型类型非常广泛,我们将重点关注用于分析晶格数据的空间模型。
数据集:纽约州北部的白血病
为了说明如何与空间模型拟合,将使用纽约白血病数据集。该数据集记录了普查区纽约州北部的许多白血病病例。数据集中的一些变量是:
Cases:1978-1982年期间的白血病病例数。POP8:1980年人口。PCTOWNHOME:拥有房屋的人口比例。PCTAGE65P:65岁以上的人口比例。AVGIDIST:到最近的三氯乙烯(TCE)站点的平均反距离。
鉴于有兴趣研究纽约州北部的白血病风险,因此首先要计算预期的病例数。这是通过计算总死亡率(总病例数除以总人口数)并将其乘以总人口数得出的:
rate <- sum(NY8$Cases) / sum(NY8$POP8)
NY8$Expected <- NY8$POP8 * rate
一旦获得了预期的病例数,就可以使用标准化死亡率(SMR)来获得原始的风险估计,该标准是将观察到的病例数除以预期的病例数得出的:
NY8$SMR <- NY8$Cases / NY8$Expected
疾病作图
在流行病学中,重要的是制作地图以显示相对风险的空间分布。在此示例中,我们将重点放在锡拉库扎市以减少生成地图的计算时间。因此,我们用锡拉丘兹市的区域创建索引:
# Subset Syracuse city
syracuse <- which(NY8$AREANAME == "Syracuse city")
可以使用函数spplot(在包中sp)简单地创建疾病图:
library(viridis)
## Loading required package: viridisLite
spplot(NY8[syracuse, ], "SMR", #at = c(0.6, 0.9801, 1.055, 1.087, 1.125, 13),
col.regions = rev(magma(16))) #gray.colors(16, 0.9, 0.4))
## Loading required package: viridisLite
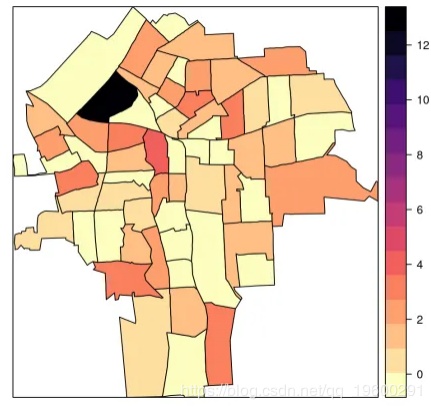
可以轻松创建交互式地图
请注意,先前的地图还包括11个受TCE污染的站点的位置,可以通过缩小看到它。
混合效应模型
泊松回归
我们将考虑的第一个模型是没有潜在随机效应的Poisson模型,因为这将提供与其他模型进行比较的基准。
模型 :
请注意,它的glm功能类似于该功能。在此,参数 E用于预期的案例数。或 设置了其他参数来计算模型参数的边际
(使用control.predictor)并计算一些模型选择标准 (使用control.compute)。
接下来,可以获得模型的摘要:
summary(m1)
##
## Call:
## Time used:
## Pre = 0.368, Running = 0.0968, Post = 0.0587, Total = 0.524
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -0.065 0.045 -0.155 -0.065 0.023 -0.064 0
## AVGIDIST 0.320 0.078 0.160 0.322 0.465 0.327 0
##
## Expected number of effective parameters(stdev): 2.00(0.00)
## Number of equivalent replicates : 140.25
##
## Deviance Information Criterion (DIC) ...............: 948.12
## Deviance Information Criterion (DIC, saturated) ....: 418.75
## Effective number of parameters .....................: 2.00
##
## Watanabe-Akaike information criterion (WAIC) ...: 949.03
## Effective number of parameters .................: 2.67
##
## Marginal log-Likelihood: -480.28
## Posterior marginals for the linear predictor and
## the fitted values are computed
具有随机效应的泊松回归
可以通过 在线性预测变量中包括iid高斯随机效应,将潜在随机效应添加到模型中,以解决过度分散问题。
现在,该模式的摘要包括有关随机效果的信息:
summary(m2)
##
## Call:
## Time used:
## Pre = 0.236, Running = 0.315, Post = 0.0744, Total = 0.625
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -0.126 0.064 -0.256 -0.125 -0.006 -0.122 0
## AVGIDIST 0.347 0.105 0.139 0.346 0.558 0.344 0
##
## Random effects:
## Name Model
## ID IID model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 3712.34 11263.70 3.52 6.94 39903.61 5.18
##
## Expected number of effective parameters(stdev): 54.95(30.20)
## Number of equivalent replicates : 5.11
##
## Deviance Information Criterion (DIC) ...............: 926.93
## Deviance Information Criterion (DIC, saturated) ....: 397.56
## Effective number of parameters .....................: 61.52
##
## Watanabe-Akaike information criterion (WAIC) ...: 932.63
## Effective number of parameters .................: 57.92
##
## Marginal log-Likelihood: -478.93
## Posterior marginals for the linear predictor and
## the fitted values are computed
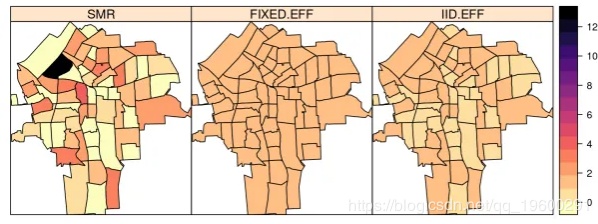
添加点估计以进行映射
这两个模型估计 可以被添加到 SpatialPolygonsDataFrame NY8
NY8$FIXED.EFF <- m1$summary.fitted[, "mean"]
NY8$IID.EFF <- m2$summary.fitted[, "mean"]
spplot(NY8[syracuse, ], c("SMR", "FIXED.EFF", "IID.EFF"),
col.regions = rev(magma(16)))
晶格数据的空间模型
格子数据涉及在不同区域(例如,邻里,城市,省,州等)测量的数据。出现空间依赖性是因为相邻区域将显示相似的目标变量值。
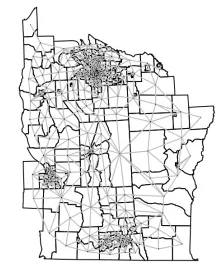
邻接矩阵
可以使用poly2nbpackage中的函数来计算邻接矩阵 spdep。如果其边界 至少在某一点上接触 ,则此功能会将两个区域视为邻居:
这将返回一个nb具有邻域结构定义的对象:
NY8.nb
## Neighbour list object:
## Number of regions: 281
## Number of nonzero links: 1624
## Percentage nonzero weights: 2.056712
## Average number of links: 5.779359
另外, 当多边形的重心 已知时,可以绘制对象:
plot(NY8)
plot(NY8.nb, coordinates(NY8), add = TRUE, pch = ".", col = "gray")
回归模型
通常情况是,除了(y_i )之外,我们还有许多协变量 (X_i )。因此,我们可能想对(X_i )回归 (y_i )。除了 协变量,我们可能还需要考虑数据的空间结构。
可以使用不同类型的回归模型来建模晶格数据:
- 广义线性模型(具有空间随机效应)。
- 空间计量经济学模型。
线性混合模型
一种常见的方法(对于高斯数据)是使用
具有随机效应的线性回归:
[
Y = X beta + Zu + varepsilon
]
随机效应的向量(u )被建模为多元正态分布:
[
u sim N(0, sigma ^ 2_u Sigma)
]
( Sigma )的定义是,它会引起与相邻区域的更高相关性,(Z )是随机效果的设计矩阵,而
( varepsilon_i sim N(0, sigma ^ 2),i = 1, ldots,n )是一个误差项。
空间随机效应的结构
在( Sigma )中包括空间依赖的方法有很多:
- 同步自回归(SAR):
[
Sigma ^ {-1} = [(I- rho W)'(I- rho W)]
]
- 条件自回归(CAR):
[
Sigma ^ {-1} =(I- rho W)
]
- (ICAR):
[
Sigma ^ {-1} = diag(n_i)– W
]
(n_i )是区域(i )的邻居数。 - ( Sigma_ {i,j} )取决于(d(i,j))的函数。例如:
[
Sigma_ {i,j} = exp {-d(i,j)/ phi }
]
- 矩阵的“混合”(Leroux等人的模型):
[
Sigma = [(1 – lambda)I_n + lambda M] ^ {-1}; lambda in(0,1)
]
ICAR模型
第一个示例将基于ICAR规范。请注意, 使用f-函数定义空间潜在效果。这将需要 一个索引来识别每个区域中的随机效应,模型的类型 和邻接矩阵。为此,将使用稀疏矩阵。
##
## Call:
## Time used:
## Pre = 0.298, Running = 0.305, Post = 0.0406, Total = 0.644
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -0.122 0.052 -0.226 -0.122 -0.022 -0.120 0
## AVGIDIST 0.318 0.121 0.075 0.320 0.551 0.324 0
##
## Random effects:
## Name Model
## ID Besags ICAR model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 3.20 1.67 1.41 2.79 7.56 2.27
##
## Expected number of effective parameters(stdev): 46.68(12.67)
## Number of equivalent replicates : 6.02
##
## Deviance Information Criterion (DIC) ...............: 904.12
## Deviance Information Criterion (DIC, saturated) ....: 374.75
## Effective number of parameters .....................: 48.31
##
## Watanabe-Akaike information criterion (WAIC) ...: 906.77
## Effective number of parameters .................: 44.27
##
## Marginal log-Likelihood: -685.70
## Posterior marginals for the linear predictor and
## the fitted values are computed
BYM模型
Besag,York和Mollié模型包括两个潜在的随机效应:ICAR 潜在效应和高斯iid潜在效应。线性预测变量( eta_i )
为:
[
eta_i = alpha + beta AVGIDIST_i + u_i + v_i
]
- (u_i )是iid高斯随机效应
- (v_i )是内在的CAR随机效应
##
## Call:
## Time used:
## Pre = 0.294, Running = 1, Post = 0.0652, Total = 1.36
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -0.123 0.052 -0.227 -0.122 -0.023 -0.121 0
## AVGIDIST 0.318 0.121 0.075 0.320 0.551 0.324 0
##
## Random effects:
## Name Model
## ID BYM model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant
## Precision for ID (iid component) 1790.06 1769.02 115.76 1265.24
## Precision for ID (spatial component) 3.12 1.36 1.37 2.82
## 0.975quant mode
## Precision for ID (iid component) 6522.28 310.73
## Precision for ID (spatial component) 6.58 2.33
##
## Expected number of effective parameters(stdev): 47.66(12.79)
## Number of equivalent replicates : 5.90
##
## Deviance Information Criterion (DIC) ...............: 903.41
## Deviance Information Criterion (DIC, saturated) ....: 374.04
## Effective number of parameters .....................: 48.75
##
## Watanabe-Akaike information criterion (WAIC) ...: 906.61
## Effective number of parameters .................: 45.04
##
## Marginal log-Likelihood: -425.65
## Posterior marginals for the linear predictor and
## the fitted values are computed
Leroux 模型
该模型是使用矩阵的“混合”(Leroux等人的模型)
定义的,以定义潜在效应的精度矩阵:
[
Sigma ^ {-1} = [(1- lambda)I_n + lambda M]; lambda in(0,1)
]
为了定义正确的模型,我们应采用矩阵(C )如下:
[
C = I_n – M; M = diag(n_i)– W
]
然后,( lambda_ {max} = 1 )和
[
Sigma ^ {-1} =
frac {1} { tau}(I_n- frac { rho} { lambda_ {max}} C)=
frac {1} { tau}(I_n- rho(I_n – M))= frac {1} { tau}((1- rho)I_n + rho M)
]
为了拟合模型,第一步是创建矩阵(M ):
我们可以检查最大特征值( lambda_ {max} )是一个:
max(eigen(Cmatrix)$values)
## [1] 1
## [1] 1
该模型与往常一样具有功能inla。注意,(C )矩阵使用参数
传递给f函数Cmatrix:
##
## Call:
## Time used:
## Pre = 0.236, Running = 0.695, Post = 0.0493, Total = 0.98
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -0.128 0.448 -0.91 -0.128 0.656 -0.126 0.075
## AVGIDIST 0.325 0.122 0.08 0.327 0.561 0.330 0.000
##
## Random effects:
## Name Model
## ID Generic1 model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 2.720 1.098 1.27 2.489 5.480 2.106
## Beta for ID 0.865 0.142 0.47 0.915 0.997 0.996
##
## Expected number of effective parameters(stdev): 52.25(13.87)
## Number of equivalent replicates : 5.38
##
## Deviance Information Criterion (DIC) ...............: 903.14
## Deviance Information Criterion (DIC, saturated) ....: 373.77
## Effective number of parameters .....................: 53.12
##
## Watanabe-Akaike information criterion (WAIC) ...: 906.20
## Effective number of parameters .................: 48.19
##
## Marginal log-Likelihood: -474.94
## Posterior marginals for the linear predictor and
## the fitted values are computed
空间计量经济学模型
空间计量经济学是通过 对空间建模略有不同的方法开发的。除了使用潜在效应,还可以对空间 依赖性进行显式建模。
同步自回归模型(SEM)
该模型包括协变量和误差项的自回归:
[
y = X beta + u; u = rho Wu + e; e sim N(0, sigma ^ 2)
]
[
y = X beta + varepsilon; varepsilon sim N(0, sigma ^ 2(I- rho W)^ {-1}(I- rho W')^ {-1})
]
空间滞后模型(SLM)
该模型包括协变量和响应的自回归:
[
y = rho W y + X beta + e; e sim N(0, sigma ^ 2)
]
[
y =(I- rho W)^ {-1} X beta + varepsilon; varepsilon sim N(0, sigma ^ 2(I- rho W)^ {-1}(I- rho W')^ {-1})
]
潜在影响slm
现在包括一个实验所谓的新的潜在影响slm,以 符合以下模型:
[
mathbf {x} =(I_n- rho W)^ {-1}(X beta + e)
]
该模型的元素是:
- (W )是行标准化的邻接矩阵。
- ( rho )是空间自相关参数。
- (X )是协变量的矩阵,系数为( beta )。
- (e )是具有方差( sigma ^ 2 )的高斯iid误差。
该slm潜效果的实验,它可以 与所述线性预测其他效果组合。
模型定义
为了定义模型,我们需要:
X:协变量矩阵W:行标准化的邻接矩阵Q:系数( beta )的精确矩阵- 范围( RHO ) ,通常由本征值定义
slm潜在作用是通过参数传递 args.sm。在这里,我们创建了一个具有相同名称的列表,以将 所有必需的值保存在一起:
#Arguments for 'slm'
args.slm = list(
rho.min = rho.min ,
rho.max = rho.max,
W = W,
X = mmatrix,
Q.beta = Q.beta
)
此外,还设置了精度参数( tau )和空间 自相关参数( rho )的先验:
- #Prior on rho
hyper.slm = list(
prec = list(
prior = "loggamma", param = c(0.01, 0.01)),
rho = list(initial=0, prior = "logitbeta", param = c(1,1))
)
先前的定义使用具有不同参数的命名列表。参数 prior定义了使用之前param及其参数。在此,为 精度分配了带有参数(0.01 )和(0.01 )的伽玛先验值,而 为空间自相关参数指定了带有参数(1 ) 和(1 )的beta先验值(即a间隔(((1,1)))中的均匀先验。
模型拟合
## Call:
## Time used:
## Pre = 0.265, Running = 1.2, Post = 0.058, Total = 1.52
## Random effects:
## Name Model
## ID SLM model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 8.989 4.115 3.709 8.085 19.449 6.641
## Rho for ID 0.822 0.073 0.653 0.832 0.936 0.854
##
## Expected number of effective parameters(stdev): 62.82(15.46)
## Number of equivalent replicates : 4.47
##
## Deviance Information Criterion (DIC) ...............: 902.32
## Deviance Information Criterion (DIC, saturated) ....: 372.95
## Effective number of parameters .....................: 64.13
##
## Watanabe-Akaike information criterion (WAIC) ...: 905.19
## Effective number of parameters .................: 56.12
##
## Marginal log-Likelihood: -477.30
## Posterior marginals for the linear predictor and
## the fitted values are computed
系数的估计显示为随机效应的一部分:
round(m.slm$summary.random$ID[47:48,], 4)
## ID mean sd 0.025quant 0.5quant 0.975quant mode kld
## 47 47 0.4634 0.3107 -0.1618 0.4671 1.0648 0.4726 0
## 48 48 0.2606 0.3410 -0.4583 0.2764 0.8894 0.3063 0
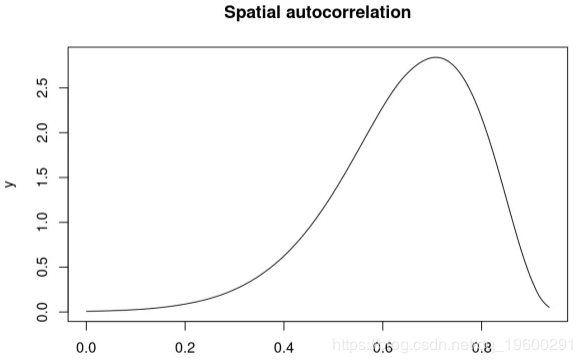
空间自相关以内部比例报告(即 0到1 之间),并且需要重新缩放:
## Call:
## Time used:
## Pre = 0.265, Running = 1.2, Post = 0.058, Total = 1.52
## Random effects:
## Name Model
## ID SLM model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for ID 8.989 4.115 3.709 8.085 19.449 6.641
## Rho for ID 0.822 0.073 0.653 0.832 0.936 0.854
##
## Expected number of effective parameters(stdev): 62.82(15.46)
## Number of equivalent replicates : 4.47
##
## Deviance Information Criterion (DIC) ...............: 902.32
## Deviance Information Criterion (DIC, saturated) ....: 372.95
## Effective number of parameters .....................: 64.13
##
## Watanabe-Akaike information criterion (WAIC) ...: 905.19
## Effective number of parameters .................: 56.12
##
## Marginal log-Likelihood: -477.30
## Posterior marginals for the linear predictor and
## the fitted values are computed
系数的估计显示为随机效应的一部分:
round(m.slm$summary.random$ID[47:48,], 4)
## ID mean sd 0.025quant 0.5quant 0.975quant mode kld
## 47 47 0.4634 0.3107 -0.1618 0.4671 1.0648 0.4726 0
## 48 48 0.2606 0.3410 -0.4583 0.2764 0.8894 0.3063 0
空间自相关以内部比例报告(即 0到1 之间),并且需要重新缩放:
## Mean 0.644436
## Stdev 0.145461
## Quantile 0.025 0.309507
## Quantile 0.25 0.556851
## Quantile 0.5 0.663068
## Quantile 0.75 0.752368
## Quantile 0.975 0.869702
plot(marg.rho, type = "l", main = "Spatial autocorrelation")
结果汇总
NY8$ICAR <- m.icar$summary.fitted.values[, "mean"]
NY8$BYM <- m.bym$summary.fitted.values[, "mean"]
NY8$LEROUX <- m.ler$summary.fitted.values[, "mean"]
NY8$SLM <- m.slm$summary.fitted.values[, "mean"]
spplot(NY8[syracuse, ],
c("FIXED.EFF", "IID.EFF", "ICAR", "BYM", "LEROUX", "SLM"),
col.regions = rev(magma(16))
)
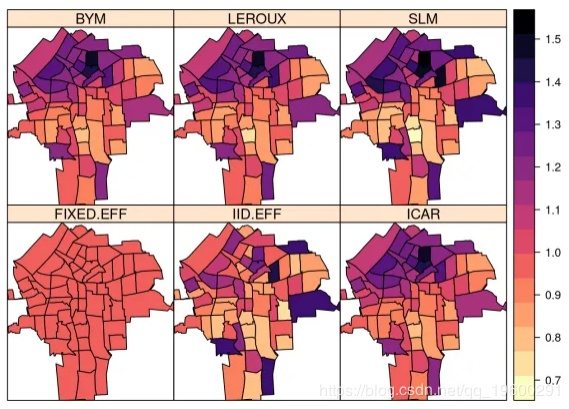
注意空间模型如何产生相对风险的更平滑的估计。
为了选择最佳模型, 可以使用上面计算的模型选择标准:
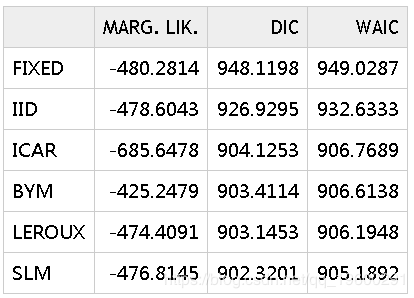
参考文献
Bivand, R., E. Pebesma and V. Gómez-Rubio (2013). Applied spatial dataanalysis with R. Springer-Verlag. New York.

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容







所有评论(0)