深度学习(五):神经网络训练不起来怎么办
深度学习(五):神经网络训练不起来怎么办梯度很小的时候无法判断是local minimalocal\ minimalocal minima还是saddle pointsaddle\ pointsaddle point,以下是判断的一个方法的数学推导Tayler Series ApproximationTayler\ Series\ App
深度学习(五):神经网络训练不起来怎么办
梯度很小的时候
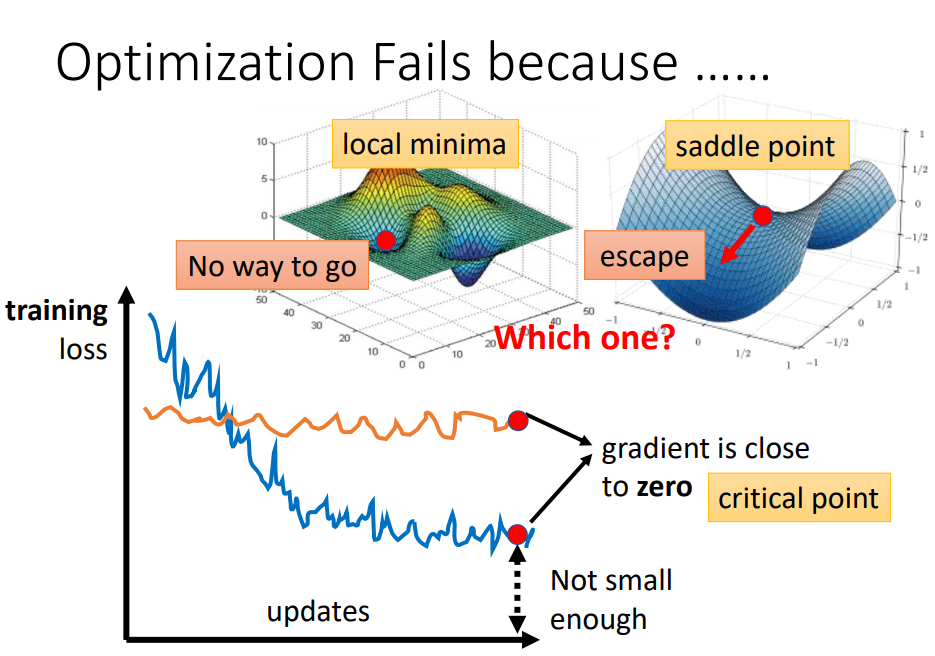
无法判断是local minimalocal\ minimalocal minima还是saddle pointsaddle\ pointsaddle point,以下是判断的一个方法的数学推导Tayler Series ApproximationTayler\ Series\ ApproximationTayler Series Approximation:
首先,L(θ)≈L(θ′)+(θ−θ′)Tg+12(θ−θ′)TH(θ−θ′)\mathbf {L(\theta) \approx L(\theta^{'})+(\theta-\theta^{'})^T {\color {green}g}+\frac {1}{2}(\theta-{\color {green}\theta^{'}})^T{\color{red}H}(\theta-{\color {green}\theta^{'}})}L(θ)≈L(θ′)+(θ−θ′)Tg+21(θ−θ′)TH(θ−θ′),其中,Gradient g\mathbf {Gradient}\ {\color {green}g}Gradient g可以用如下的向量表示:
g=∇L(θ′)gi=∂L(θ)∂θi{\color {green}g}=\nabla L(\theta^{'})\qquad \qquad\qquad \qquad {\color {green}g}_{i}=\frac{\partial L(\theta)}{\partial \theta_{i}}g=∇L(θ′)gi=∂θi∂L(θ)
HHH是HessianHessianHessian矩阵,可以表示为如下形式:
Hij=∂2∂θi∂θjL(θ′)\mathbf {H_{ij}=\frac{\partial^2}{\partial \theta_{i}\partial \theta_j}L(\theta^{'})}Hij=∂θi∂θj∂2L(θ′)
下图是公式的推导具体过程,通过下图对HessianHessianHessian矩阵的特征值的大小的判断可以判断出是local minimalocal\ minimalocal minima还是saddle pointsaddle\ pointsaddle point



下面是对Gradient\mathbf {Gradient}Gradient的图的直观表示方法: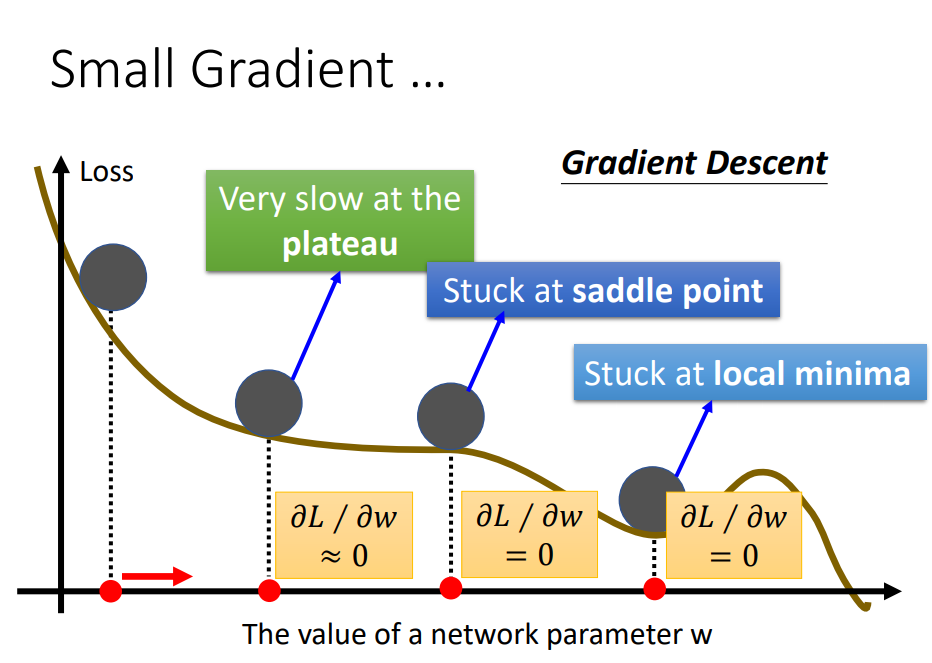
batch\mathbf {batch}batch和momentum\rm {\mathbf {momentum}}momentum的训练小技巧
接下来要介绍下深度学习中关于batch\mathbf {batch}batch和momentum\rm {\mathbf {momentum}}momentum的相关基础姿势的简单介绍。敬请期待~

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)