深度学习——神经网络前向传播和反向求导过程

1. 神经网络的基本结构

1.1 神经网络引入

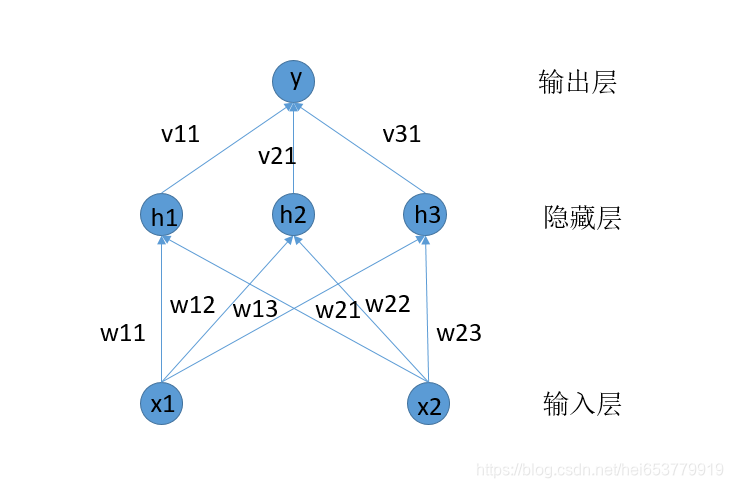
如图所示的是一个简单的神经网络结构，通常情况下，一个神经网络包含以下三种基本的机构。

1. 输入层，图中展示为{$x_1,x_2$}
2. 隐藏层，图中展示为{$h_1,h_2,h_3$}
3. 输出层，图中展示为{$y$}

我们假设某一个数据集D={$(X_1,Y_1),........(X_N,Y_N)$}，其中$X$表示样本，Y表示该样本的标签。
每一个样本具有两个属性，分别为$(x_1,x_2)$(如输入层所示)。对于权重，主要是输入层到隐藏层的权重以及隐藏层到输出层的权重。

根据上面的图示，我们可以确定的是对于输入层的每一个神经元，其需要分布向三个隐藏层的神经元进行输入。对于输入层的第一个神经元，定义三个权重值$[w_{11},w_{12},w_{13}]$，下标的第一部分表示是第一个神经元，第二部分表示的是输入的隐藏的神经元。对于输入层的第二个神经元，定义权重为$[w_{21},w_{22},v_{23}]$，将两个w构成一个矩阵表示为[$[w_{11},w_{12},w_{13}]$，$[w_{21},w_{22},w_{23}]$]。

对于隐藏层，其向输出层输出的过程就简单了很多，每一个节点向输出层的一个节点输出，则可以定义权重为[$[v_1]，[v_2]，[v_3]$]

1.2 前向传播过程

现在，我们假定一个训练样本X是[[0.4],[0.5]]。现在将样本X投入到神经网络中，我们假定权重W初始为[[0.1,0.3,0.5]，[0.2,0.4,0.6]]，首先是输入层的第一个神经元的计算为：
$$0.4\ast 0.1，0.4\ast 0.3,0.4\ast 0.5$$
将分别传递个三个隐藏层的神经元，然后是第二个输入层神经元：
$$0.5\ast 0.2,0.5\ast 0.4,0.5\ast 0.6$$
将其分别传递三个隐藏层的神经元。每一个神经元将接受到的输入进行求和：
$$0.4\ast 0.1+0.5\ast 0.2，0.4\ast 0.3+0.5\ast 0.4，0.4\ast 0.5+0.5\ast 0.6$$
我们可以向向量的方式来表示这种乘法相加的过程。
$$H=W^{T}X$$
$$\begin{array}{c}{h}_1:0.4\ast 0.1+0.5\ast 0.2=0.14\\ h_2:0.4\ast 0.3+0.5\ast 0.4=0.22\\ h_3:0.4\ast 0.5+0.5\ast 0.6=0.50\end{array}$$
我们使用Numpy代码来表示这个部分

X = np.array([0.4,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
H = np.dot(X,W1) + B1
H = H.T

\begin{matrix}
h_1:0.40.1+0.50.2+0.1=0.24\
h_2:0.40.3+0.50.4+0.2 =0.52\
h_3:0.40.5+0.50.6+0.3=0.80\
\end{matrix}
$$
在上述的代码中，我们又添加了一个偏置项B=$[0.1,0.2,0.3]$，不要担心，偏置项是一个常数，是在乘法计算完成之后添加的一个常量，不会对我们上面叙述的传播过程产生影响。计算结果如图所示：

OK,我们已经得到了隐藏层的向量，下一步，我们需要根据权重V，来计算出最后的输出层结果。我们假设V为[[0.1],[0.2],[0.3]]。同理，我们在这里加上一个偏置项B2为[[0.1]]这个计算过程比之前的两个神经元的计算过程要简单的多，所以这里，不过多的进行展示，直接给出代码：

V = np.array([[0.1],[0.2],[0.3]])
B2 = np.array([0.1])
Y = np.dot(V.T,A1) + B2

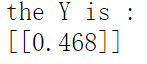
至此，一个简单的前向传播过程就结束了。

1.3 激活函数的引入

下面，我们考虑这样一个问题，根据上面的计算，我们设定权重W是一个(3,2)的矩阵，V是一个(3,1)的矩阵，那么是不是可以直接设定一个$V^{T}W=Z(1,2)$的矩阵，来省略隐藏层呢？这就印引出了激活函数的作用。

在上面的计算中，所有的矩阵乘法都相当于线性操作，设置多个网络层，多个权重矩阵相乘和直接设定一个矩阵相乘输出并没有太大的区别。

所以，我们引入激活函数，激活函数的作用是将线性操作转换成非线性的操作，这里我们只举一个sigmoid的激活函数。(其他的激活函数会在后面的文章中进行具体的阐述。)

首先，给出sigmoid函数的函数图像：

我们简单的介绍sigmoid函数的两个特性：

1. 易于求导 sigmoid函数的导数为 $sigmoid(x)-(sigmoid(x){)}^2$
2. 非线性的函数。

OK，下面我们将sigmod函数加入到我们之前的传播过程中，我们将每一次的结果进行一个sigmoid的激活过程。具体代码如下：

def sigmoid(x):
    return 1/(1+np.exp(-x))
X = np.array([0.4,0.5])
W = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
net_1 = np.dot(X,W1) + B1
H = sigmoid(net_1)
V = np.array([[0.1],[0.2],[0.3]])
B2 = np.array([0.1])
net_2 = np.dot(V.T,A1) + B2
Y = sigmoid(net_2)

对应的输出结果为：

1.4 误差函数的引入

我们前向传播的计算结果已经计算出来了，也就是说我们有了预测的结果Y，下一步，我们要做的就是衡量预测结果和真实结果的误差值。这里，我们只说明一个误差计算函数——均分误差(MSE)(其他的误差函数会在后面的文章中进行介绍)。
我们首先给出计算MSE的计算公式：
$$J=1/2\ast \sum _{i=1}^m(y_{ri}-y_i)$$

其中，$y_{ri}$表示真实的Y的第i个属性的属性值，$y_i$表示预测的第i个属性的输出。在我们上述描述的网络结构中，只有一个输出$y_1$，所以误差的计算为：
$$J=1/2\ast \sum _{i=1}^1(y_{ri}-y_i)$$

下面，我们用代码来实现一下：

def calMSE(label,prediction):
    return 1/2 *np.sum(pow((label-prediction),2))

我们现在假设Y的真实值为1.0，则计算出来的误差值为：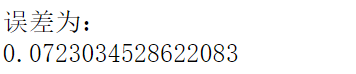

1.5 前向传播总结

在前向传播的过程中，我们定义了权重，激活函数，以及误差计算。将上面的过程总结一下，用代码来表示为：

def sigmoid(x):
    return 1/(1+np.exp(-x))
def calMSE(label,prediction):
    return 1/2 *np.sum(pow((label-prediction),2))
class NetWorks:
    def __init__(self):
        self.W = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
        self.B1 = np.array([0.1,0.2,0.3])
        self.V = np.array([[0.1],[0.2],[0.3]])
        self.B2 = np.array([0.1])
    def forward(self,X):
        net_1 = np.dot(X,W1) + B1
        H = sigmoid(net_1)
        net_2 = np.dot(V.T,H) + B2
        Y = sigmoid(net_2)
        return Y
X = np.array([0.4,0.5])
labelY = np.array([1.0])
nn = NetWorks()
Y = nn.forward(X)
E = calMSE(labelY,Y)

这其中，$ne{t}_1$表示没有激活之前的[h1,h2,h3]，$ne{t}_2$表示没有激活之前的[y]

2、反向传播(BP)算法

2.1 前向传播的回顾

根据，我们之前的计算，我们获得了前向传播的的预测结果和误差值，下面我们来回忆我们之前定义的网络结构：

在上面的图中，增加了偏置B1和B2。

2.2 隐藏层到输出层梯度计算

我们已经知道了MSE计算出来的误差E，对于V11的梯度，我们的计算公式为:
$$\frac{\delta E}{V_{11}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta V_{11}}$$
同理，我们可以求出，$V_{21},V_{31}$的梯度为：
$$\frac{\delta E}{V_{21}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta V_{21}}$$
$$\frac{\delta E}{V_{31}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta V_{31}}$$

从上面的计算过程我们可以发现：$\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}$在整个计算过程中多次出现，那么，我们就可以只计算一次，保存计算结果。直接用于后面的两次计算 。
其中：
$$\frac{\delta E}{\delta Y}=\frac{\delta \frac{1}{2}(labelY-Y{)}^2}{\delta Y}=Y-labelY$$
$$\frac{\delta Y}{\delta ne{t}_2}=\frac{\delta sigmoid(ne{t}_2)}{\delta ne{t}_2}=sigmoid(ne{t}_2)-sigmoid(ne{t}_2{)}^2$$
我们用代码将上述两个公式计算出来:

delta_Y = labelY - Y
delta_Y_net2 = sigmoid(net_2) - sigmoid(net_2)*sigmoid(net_2)

计算出来公共梯度值之后，我们来分别计算关于$V_{11}，V_{21}，V_{31}$的结果值。用代码表示如下：

delta_V = delta_Y * delta_Y_net2 * H

H中包含的是三个隐藏层状态的输入值[h1,h2,h3]。计算的的结果为：

至此，我们计算出来的输出层的权重V的梯度，下一步，我们就可以利用梯度下降算法来更新梯度V的值。我们设定学习率α为0.01。则更新后的$V_{11}，V_{21}，V_{31}$的值为:
$$[V_{11},V_{21},V_{31}{]}_{new}=[V_{11},V_{21},V_{31}{]}_{old}-\alpha \ast [\frac{\delta E}{V_{11}},\frac{\delta E}{V_{21}},\frac{\delta E}{V_{31}}]$$
我们用python代码来实现以下：

V = V - (learning_rate * delta_V).reshape(3,1)

输出的结果为：

2.3 输入层到隐藏层梯度计算

相比于隐藏层到输出层的梯度计算，输入层到隐藏层的梯度计算要麻烦许多，下面我们来一步一步对其进行分解进行，我们再将神经网络的结构图拿过来：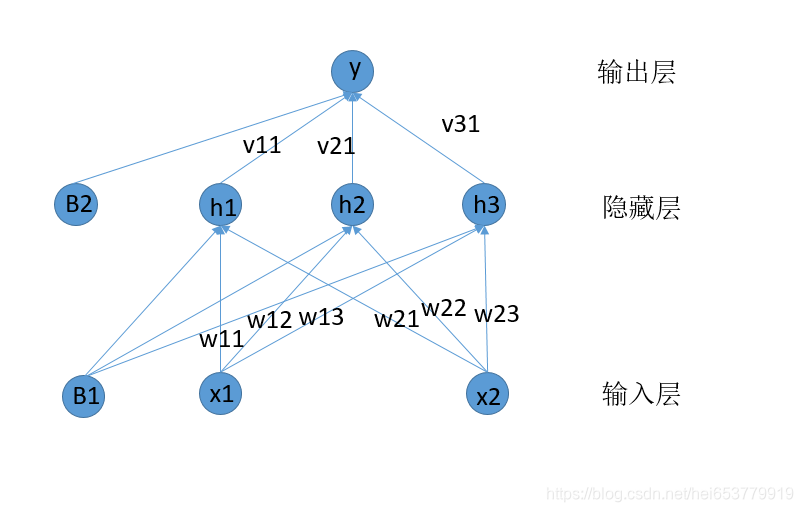

我们首先计算关于$W_{11}$的导数，有以下公式：
$$\frac{\delta E}{W_{11}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta h_1}\ast \frac{\delta h_1}{\delta ne{t}_1[0]}\ast \frac{\delta ne{t}_1[0]}{\delta W_{11}}$$
同理有关于$W_{12}和W_{13}$的导数：
$$\frac{\delta E}{W_{11}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta h_2}\ast \frac{\delta h_2}{\delta ne{t}_1[1]}\ast \frac{\delta ne{t}_1[1]}{\delta W_{12}}$$
$$\frac{\delta E}{W_{11}}=\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}\ast \frac{\delta ne{t}_2}{\delta h_3}\ast \frac{\delta h_3}{\delta ne{t}_1[2]}\ast \frac{\delta ne{t}_1[2]}{\delta W_{13}}$$

其中$ne{t}_1[0],ne{t}_1[1],ne{t}_1[2]$分别表示没有激活的h1,h2,h3。在此之前，我们已经计算出来了$\frac{\delta E}{\delta Y}\ast \frac{\delta Y}{\delta ne{t}_2}$，在此可以进行重复使用，所以，我们可以之探讨后半部分，
对于$\frac{\delta ne{t}_2}{\delta h_1}\ast \frac{\delta h_1}{\delta ne{t}_1[0]}\ast \frac{\delta ne{t}_1[0]}{\delta W_{11}}$，其计算过程如下：
$$\frac{\delta ne{t}_2}{\delta h_1}=\frac{\delta V_{11}{h}_1+V_{21}{h}_2+V_{31}{h}_3}{\delta h_1}=V_{11}$$
$$\frac{\delta h_1}{\delta ne{t}_1[0]}=(sigmoid(ne{t}_1[0]-sigmoid(ne{t}_1[0]){)}^2$$
$$\frac{\delta ne{t}_1[0]}{W_{11}}=x_1$$

同理：对于其他两个的计算过程为：
$$\frac{\delta ne{t}_2}{\delta h_2}=\frac{\delta V_{11}{h}_1+V_{21}{h}_2+V_{31}{h}_3}{\delta h_2}=V_{21}$$
$$\frac{\delta h_2}{\delta ne{t}_1[1]}=(sigmoid(ne{t}_1[1])-sigmoid(ne{t}_1[1]){)}^2$$
$$\frac{\delta ne{t}_1[1]}{W_{12}}=x_1$$
$$\frac{\delta ne{t}_2}{\delta h_3}=\frac{\delta V_{11}{h}_1+V_{21}{h}_2+V_{31}{h}_3}{\delta h_3}=V_{31}$$
$$\frac{\delta h_1}{\delta ne{t}_1[2]}=(sigmoid(ne{t}_1[2]-sigmoid(ne{t}_1[2]){)}^2$$
$$\frac{\delta ne{t}_1[2]}{W_{13}}=x_1$$

我们将中间值组成向量的的形式：
$$[\frac{\delta ne{t}_2}{\delta h_1},\frac{\delta ne{t}_2}{\delta h_2},\frac{\delta ne{t}_2}{\delta h_3}]=[V_{11},V_{21},V_{31}]$$
$$[\frac{\delta h_1}{\delta ne{t}_1[0]},\frac{\delta h_2}{\delta ne{t}_1[1]},\frac{\delta h_3}{\delta ne{t}_1[2]}]=sigmoid([ne{t}_1[0],ne{t}_1[1],ne{t}_1[2]])-sigmoid([ne{t}_1[0],ne{t}_1[1],ne{t}_1[2]]{)}^2=sigmoid(ne{t}_1)-sigmoid(ne{t}_1{)}^2$$
$$[\frac{\delta ne{t}_1[0]}{W_{11}},\frac{\delta ne{t}_1[1]}{W_{12}},\frac{\delta ne{t}_1[2]}{W_{13}}]=[x_1,x_1,x_1]$$

至此，我们计算完成了对于$x_1$输入的特征的权重的梯度值。我们用代码来实现一下：

delta_net2_H = nn.V.reshape(1,3)
delta_H_net1 = 1 - sigmoid(net_1)*sigmoid(net_1)
delta_net1_w1 = np.array([X[0],X[0],X[0]])
delta_w1 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w1

计算的结果为：

计算属性$x_2相关的权重的值和计算$x_1十分类似，这里不给出具体的过程。给出最后结果的计算公式。
$$[\frac{\delta ne{t}_2}{\delta h_1},\frac{\delta ne{t}_2}{\delta h_2},\frac{\delta ne{t}_2}{\delta h_3}]=[V_{11},V_{21},V_{31}]$$
$$[\frac{\delta h_1}{\delta ne{t}_1[0]},\frac{\delta h_2}{\delta ne{t}_1[1]},\frac{\delta h_3}{\delta ne{t}_1[2]}]=sigmoid([ne{t}_1[0],ne{t}_1[1],ne{t}_1[2]])-sigmoid([ne{t}_1[0],ne{t}_1[1],ne{t}_1[2]]{)}^2=sigmoid(ne{t}_1)-sigmoid(ne{t}_1{)}^2$$
$$[\frac{\delta ne{t}_1[0]}{W_{21}},\frac{\delta ne{t}_1[1]}{W_{22}},\frac{\delta ne{t}_1[2]}{W_{23}}]=[x_2,x_2,x_2]$$
不难发现，我们对于之前大部分的计算都可以进行重用。仅仅是最后一步发生了一些改变。给出代码及结果：

delta_Y = labelY - Y
delta_Y_net2 = sigmoid(net_2) - sigmoid(net_2)*sigmoid(net_2)
delta_V = delta_Y * delta_Y_net2 * H
delta_net2_H = nn.V.reshape(1,3)
delta_H_net1 = sigmoid(net_1) - sigmoid(net_1)*sigmoid(net_1)
delta_net1_w2 = np.array([X[1],X[1],X[1]])
delta_w2 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w2

2.4 反向传播过程总结

在反向计算梯度的过程中，我们发现，大量的结果都可以进行重用。注意，这是很重要的一点，这是后面要介绍的反向传播算法(BP)算法的基础。下面，我们用代码总结一下反向计算梯度的过程：

 def backward(self,X,labelY):
        H,net_1,net_2,Y = self.forward(X)
        delta_Y = labelY - Y
        delta_Y_net2 = sigmoid(net_2) - sigmoid(net_2)*sigmoid(net_2)
        delta_V = delta_Y * delta_Y_net2 * H
        delta_net2_H = nn.V.reshape(1,3)
        delta_H_net1 = sigmoid(net_1) - sigmoid(net_1)*sigmoid(net_1)
        delta_net1_w2 = np.array([X[1],X[1],X[1]])
        delta_w2 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w2
        delta_net1_w1 = np.array([X[0],X[0],X[0]])
        delta_w1 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w1
        return delta_w1,delta_w2

3、代码总结

learning_rate = 0.01
def sigmoid(x):
    return 1/(1+np.exp(-x))
def calMSE(label,prediction):
    return 1/2 *np.sum(pow((label-prediction),2))
class NetWorks:
    def __init__(self):
        self.W = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
        self.B1 = np.array([0.1,0.2,0.3])
        self.V = np.array([[0.1],[0.2],[0.3]])
        self.B2 = np.array([0.1])
    def forward(self,X):
        net_1 = np.dot(X,W1) + B1
        H = sigmoid(net_1)
        net_2 = np.dot(V.T,H) + B2
        Y = sigmoid(net_2)
        return H,net_1,net_2,Y
    def backward(self,X,labelY):
        H,net_1,net_2,Y = self.forward(X)
        delta_Y = labelY - Y
        delta_Y_net2 = sigmoid(net_2) - sigmoid(net_2)*sigmoid(net_2)
        delta_V = delta_Y * delta_Y_net2 * H
        delta_net2_H = nn.V.reshape(1,3)
        delta_H_net1 = sigmoid(net_1) - sigmoid(net_1)*sigmoid(net_1)
        delta_net1_w2 = np.array([X[1],X[1],X[1]])
        delta_w2 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w2
        delta_net1_w1 = np.array([X[0],X[0],X[0]])
        delta_w1 = delta_Y*delta_Y_net2*delta_net2_H * delta_H_net1*delta_net1_w1
        return delta_V,delta_w1,delta_w2
    def update(self,delta_V,delta_w1,delta_w2):
        self.V = self.V - (learning_rate * delta_V).reshape(3,1)
        delta_W = np.concatenate((delta_w1,delta_w2),axis=0)
        delta_w1 = delta_w1.reshape(1,3)
        delta_w2 = delta_w2.reshape(1,3)
        self.W = self.W - learning_rate*delta_W 

一次更新后V和W的输出为：