深度学习：激活函数（Activation Functions ）

激活函数指的是，我们在应用于神经网络中的函数，(通常)应用于在输入特征结合权重和输入特征应用仿射变换操作之后。激活函数是典型的非线性函数。ReLU是过去十年中最流行的一种。激活函数的选择与网络结构有关，而且近年来出现了许多替代方案。1、...

MarkJhon

1257人浏览 · 2021-10-05 16:17:38

MarkJhon · 2021-10-05 16:17:38 发布

激活函数指的是，我们在应用于神经网络中的函数，(通常)应用于在输入特征结合权重和输入特征应用仿射变换操作之后。激活函数是典型的非线性函数。ReLU是过去十年中最流行的一种。激活函数的选择与网络结构有关，而且近年来出现了许多替代方案。

1、Rectified Linear Units (Relu)

ReLU在正维度上是线性的，在负维度上是零。函数中的扭结是非线性的来源。正维度的线性的特性是，尽管只有负维度线的一半梯度为零，但仍可以防止梯度的非饱和(与Sigmoid相反)。

$f\left(x\right) = \max\left(0, x\right)$

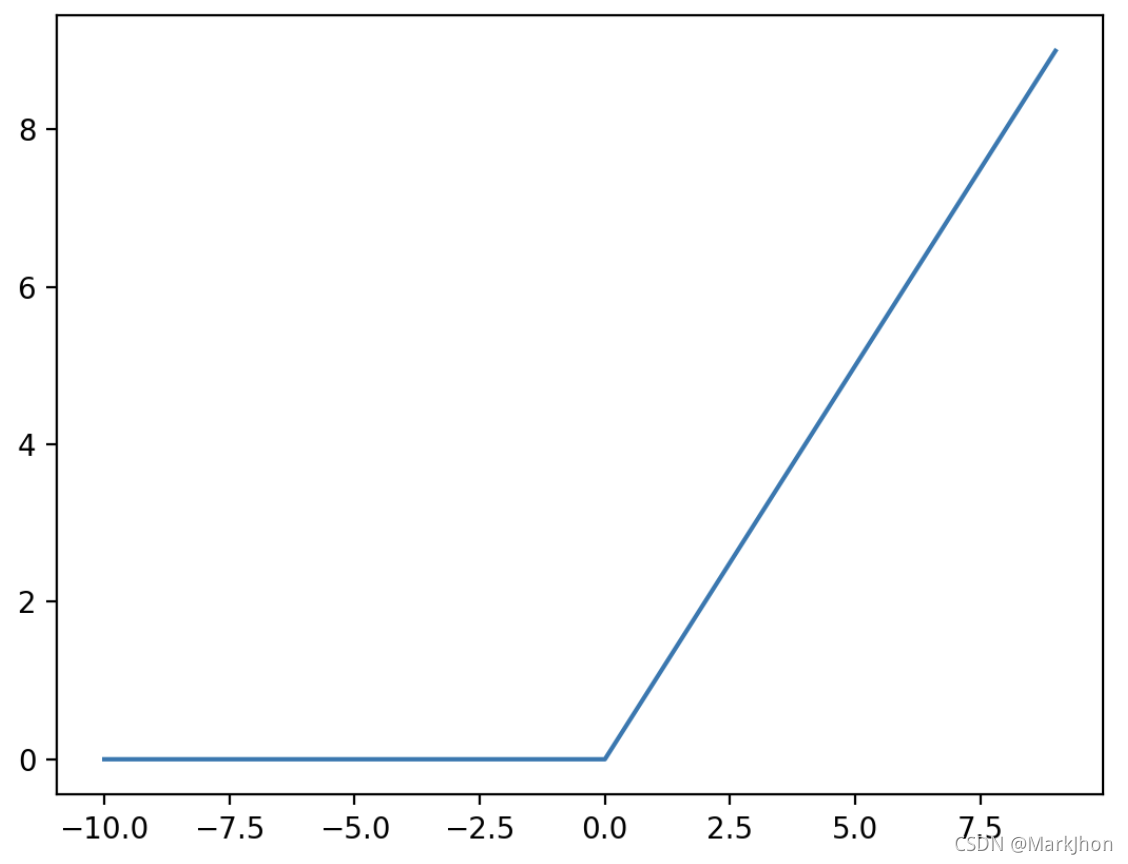
2、Sigmoid Activation

Sigmoid激活函数的缺点是:从更深的隐藏层到输入的反向传播过程中，存在急剧的梯度阻碍、梯度饱和和缓慢的收敛问题。

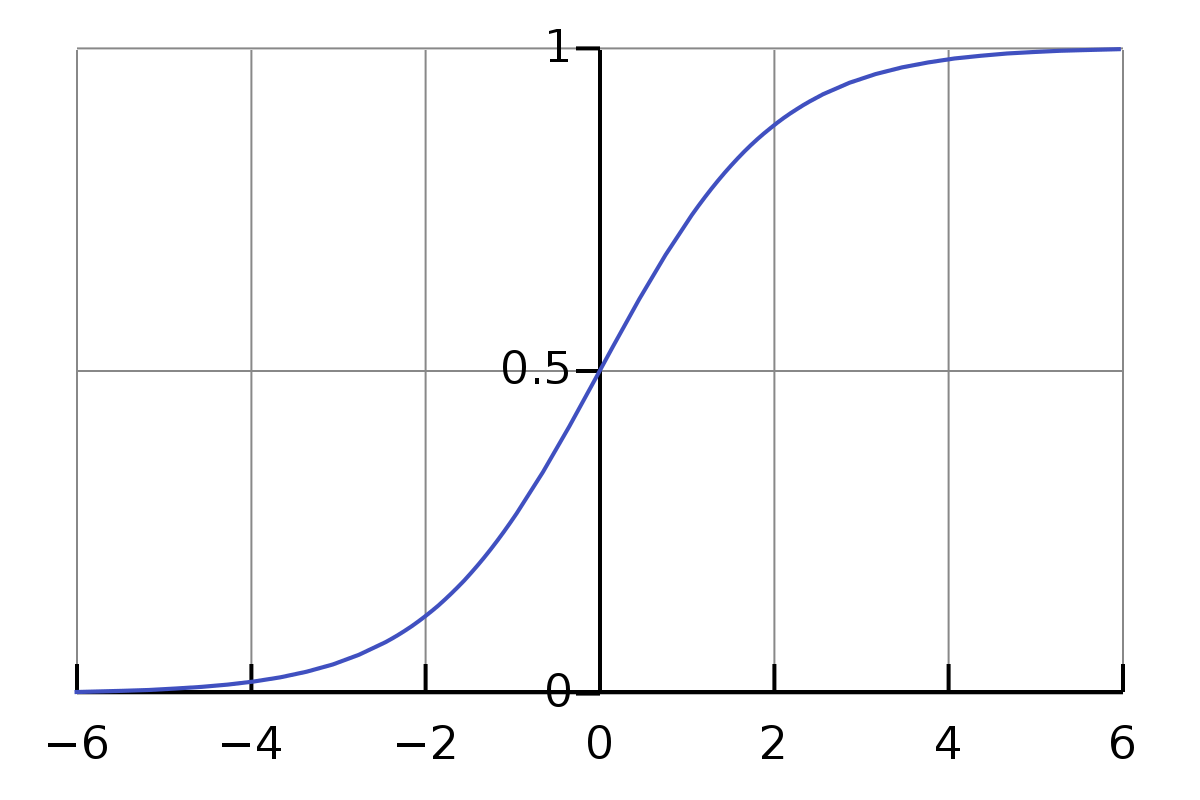
$f\left(x\right) = \frac{1}{\left(1+\exp\left(-x\right)\right)}$

3、Tanh Activation

实际上，Tanh函数比Sigmoid函数更受欢迎，因为它在多层神经网络中具有更好的性能。但Tanh并没有解决sigmoids所面临的梯度消失问题，梯度消失的问题在ReLU函数中得到有效地解决。

$f\left(x\right) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

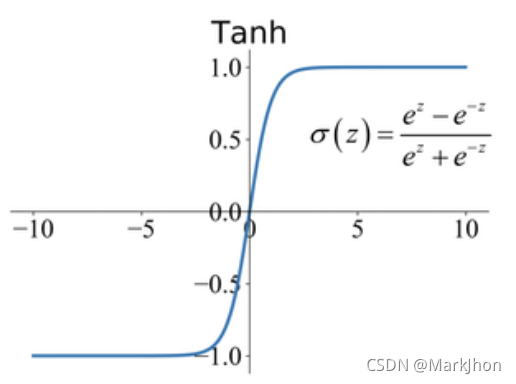
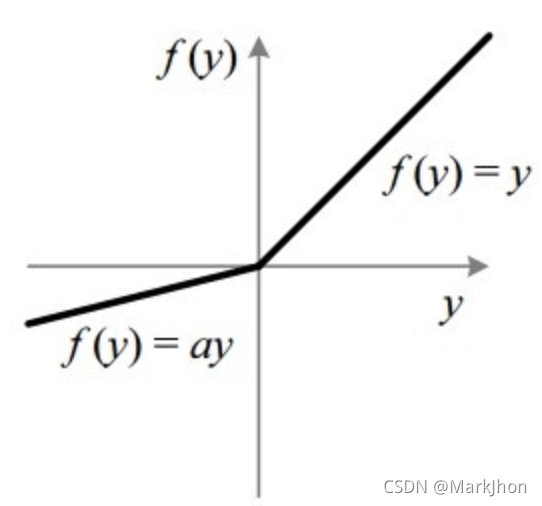
3、Leaky Relu

Leaky ReLU是一种基于ReLU的激活函数。它对负值的计算的斜率很小，不像Relu那样是平坦的斜率。斜率系数a是在训练前确定的，作为超参进行微调，在训练中不学习。这种类型的激活函数在遇到稀疏梯度的任务中可进行使用，例如训练生成式对抗网络（GAN）。

4、Gaussian Error Linear Units （GRELU）

GELU激活函数是 $x\Phi(x)$ ,在 $\Phi(x)$ 是标准高斯累积分布函数。GELU非线性用百分比来加权输入，而不是像Relu( $x\mathbf{1}_{x>0}$ )那样用符号来加权输入。所以，GELU可以被认为是一个更平滑的ReLU。

$\text{GELU}\left(x\right) = x{P}\left(X\leq{x}\right) = x\Phi\left(x\right) = x \cdot \frac{1}{2}\left[1 + \text{erf}(x/\sqrt{2})\right],$ （ $X\sim \mathcal{N}(0,1)$ ）

在实际使用中，可以使用 $0.5x\left(1+\tanh\left[\sqrt{2/\pi}\left(x + 0.044715x^{3}\right)\right]\right)$ 或者 $x\sigma\left(1.702x\right)$ 近似GRELU。但PyTorch的精确实现足够快，因此这些近似可能是不必要的。GELU被用在GBT-3, BERT, 和其他类型的Transformers中.