数据集介绍

波士顿房价数据来源于哈里森（D. Harrison）和鲁宾菲尔德（D.L. Rubinfeld）1978年发表在《环境经济学与管理杂志》（J. Environ. Economics & Management）第5卷81-102页的论文《享乐价格和对清洁空气的需求》。该数据还被用于贝尔斯利（Belsley）、库（Kuh）和威尔施（Welsch）1980年出版的《回归诊断……》（Regression diagnostics...）一书（Wiley出版社）。

        一共有14列数据，前13列可作为自变量，最后一列房价的实际价格为因变量。

变量按顺序如下：
- CRIM：城镇人均犯罪率
- ZN：用于25,000平方英尺以上地块的住宅用地比例
- INDUS：城镇非零售商业用地比例
- CHAS：查尔斯河虚拟变量（如果地块与河流相邻则为1，否则为0）
- NOX：一氧化氮浓度（每1000万部分）
- RM：每栋住宅的平均房间数
- AGE：1940年之前建造的自住单位比例
- DIS：到波士顿五个就业中心的加权距离
- RAD：通往放射状公路的可达性指数
- TAX：每10,000美元的房产税全值税率
- PTRATIO：城镇师生比例
- B：1000×(Bk - 0.63)^2，其中Bk是城镇黑人比例
- LSTAT：人口中低收入阶层的百分比
- MEDV：自住住宅的中位价值（以1000美元计）

项目原理

        为了预测房价，我们假设了自变量x（此处即为前13列数据）和预测房价z的关系为z=wx+b，我们的训练目标是，通过求解参数w和b，让房价的预测值z更加靠近真实值y（即数据集中最后一列数据）。

        怎么衡量预测值和真实值之间的误差大小呢？简单常见的就是均方误差，即。把所有数据预测结果的误差累加起来即可衡量总体的误差，这就是损失函数，即

        以只有一条数据为例，此时，把z=wx+b带入损失函数，即，其中，y为房价真实值已知（数据集最后一列），x为影响房价的自变量也已知（数据集前13列），因此Loss可以看成是参数w和b的函数，求解的目标就是找到一个w和b，使得Loss最小，即可。然后保存好求解的参数w和b，即可使用z=wx+b来预测房价。

        怎么找到最合适的w和b使Loss函数最小呢（找到函数的最低点）？梯度下降就是解决这个问题的。在本文，梯度是L对w和b的偏导数构成的向量，梯度的方向表示的是函数增加最快的方向，反方向即为函数下降的最快方向。

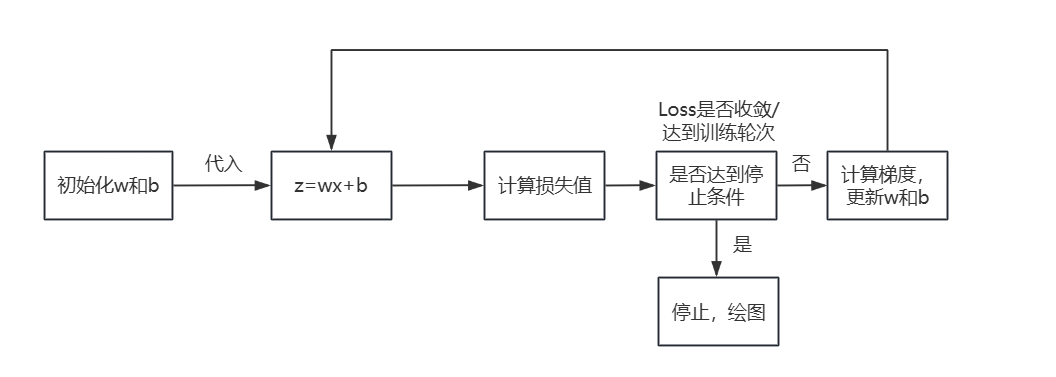
        训练思路：前向计算--计算损失--计算梯度--更新参数。具体训练过程为，首先使用随机数为w和b赋值

        ①把w和b带入z=wx+b计算预测值。这个可以理解为是前向计算。

        ②然后把预测出的z带入Loss损失函数，计算其损失并记录下来。

        ③再计算出Loss对w和b的偏导数gradient_w和gradient_b（梯度），然后w=w-gradient_w*eta，b=b-gradient_b*eta，来更新参数。更新完参数w和b之后，重复执行①，直到Loss函数值收敛。eta为设置的步长/学习率，指往梯度方向一次下降多少距离，步长小比较精准但是收敛慢，步长太大可能会错过最低点。

代码实现步骤

1、数据读取，数据集划分、归一化（注释全部为手动添加）

def load_data():
    # 读取 CSV 文件
    array = pd.read_csv(r'D:\学习\研究生专业学习\专业知识学习\学习项目\房价\波士顿房价数据集\boston.csv')
    # 将 DataFrame 转换为 NumPy 数组
    data = array.to_numpy()
    # 设置随机种子（可选，用于可重复性）
    np.random.seed(1)
    # 定义划分比例
    ratio = 0.8
    # 获取数据的总行数
    num_rows = data.shape[0]
    # 计算训练集的大小
    train_size = int(num_rows * ratio)
    # 随机生成训练集的索引
    train_indices = np.random.choice(num_rows, train_size, replace=False)
    # 创建一个布尔掩码，用于划分训练集和测试集
    mask = np.zeros(num_rows, dtype=bool)
    mask[train_indices] = True
    # 划分训练集和测试集
    training_data = data[mask]
    test_data = data[~mask]

    # 归一化处理     为什么使用训练数据的数字特征归一全部的数据？
    maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), training_data.sum(axis=0) / \
                                                                                     training_data.shape[0]
    for i in range(13):
        data[:,i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
    #     # 保存归一化后的数据到文本文件
    # np.savetxt(r'D:\学习\研究生专业学习\专业知识学习\学习项目\房价\归一化后的数据.txt', data, fmt='%.6f',delimiter=',')
    training_data = data[mask]
    test_data = data[~mask]
    return training_data, test_data, data

2、随机给w，b赋值

    def __init__(self,num_of_weights):
        # 随机产生参数的值
        np.random.seed(0)
        self.w=np.random.randn(num_of_weights,1)
        self.b=0

3、前向计算

    def forward(self,x):
        z=np.dot(x,self.w)+self.b
        return z

4、计算损失函数

    def loss(self,z,y):
        error=z-y
        num_samples=error.shape[0]
        cost=error * error
        cost=np.sum(cost)/num_samples
        return cost

5、计算梯度（偏导数）

    def gradient(self,x,y):
        z=self.forward(x)
        # L对w的偏导数  每个样本对梯度的贡献
        gradient_w=(z-y) * x
        # 得计算总梯度（平均梯度）
        gradient_w=np.mean(gradient_w,axis=0)
        # 将一维数组 gradient_w 转换为二维数组，形状为 (num_features, 1)
        # np.newaxis 是 NumPy 中的一个特殊对象，用于在数组中增加一个新的轴（维度）
        gradient_w=gradient_w[:,np.newaxis]
        #L对b的偏导
        gradient_b=z-y
        gradient_b=np.mean(gradient_b)
        return gradient_w,gradient_b

6、更新w和b

    def update(self,gradient_w,gradient_b,eta=0.01):
        self.w=self.w-gradient_w * eta
        self.b=self.b-gradient_b * eta

7、训练过程

    #一般的梯度下降法
    def train(self,x,y,iterations=100,eta=0.01):
        losses=[]
        for i in range(iterations):
            z=self.forward(x)
            L=self.loss(z,y)
            gradient_w,gradient_b=self.gradient(x,y)
            self.update(gradient_w,gradient_b,eta)
            losses.append(L)
            if(i+1)%10==0:
                print('iter为{},loss为{}'.format(i,L))
        return losses

8、绘图

#获取数据
training_data,test_data,data=load_data()
x=training_data[:,:-1]
y=training_data[:,-1:]
#创建网络
net=Network(13)
# 设置迭代次数。迭代是指模型在训练过程中，对一批数据（可以是一个样本，也可以是多个样本的批量）进行一次前向传播和一次反向传播的过程。
# epoch轮次是指模型在整个训练数据集上完成一次完整的前向传播和反向传播的过程。
num_iteration=1000
#启动训练
losses=net.train(x,y,iterations=num_iteration,eta=0.02)
# 保存模型参数
with open('model.pkl', 'wb') as f:
    pickle.dump(net, f)
print("模型参数已保存")
# 回归任务
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定中文字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号
#画出结果
plot_x=np.arange(len(losses))
# plot_x=np.arange(num_iteration)
plot_y=np.array(losses)
plt.plot(plot_x,plot_y)
plt.xlabel('迭代次数', fontsize=14, color='blue')  # 添加 x 轴标题
plt.ylabel('损失值', fontsize=14, color='blue')      # 添加 y 轴标题
plt.title('Training Loss Over Iterations', fontsize=16, color='green')  # 添加图表标题
plt.show()

实验结果

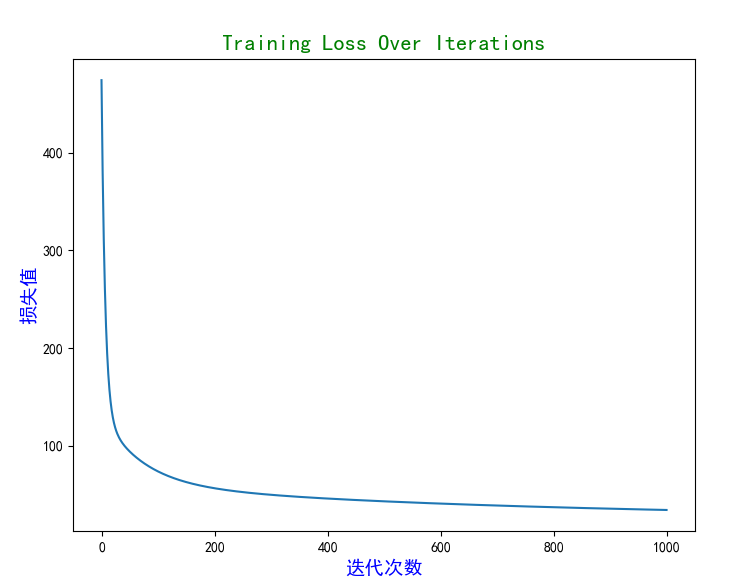
迭代到100此左右损失值就逐渐收敛，随后记录此时的w和b用于预测未知的房价数据。

优化与改进方向

①把一般的梯度下降法改为小批量的随机梯度下降。一般的梯度下降计算w和b的偏导时使用了所有数据，每一行数据算一个偏导，然后累加再平均下来得到平均梯度，数据量大时较慢，但是也因此曲线比较平滑。小批量梯度下降每次迭代抽取一小部分样本代表总体去计算梯度，因此曲线会有抖动，但速度更快。下图是小批量梯度下降的结果图。

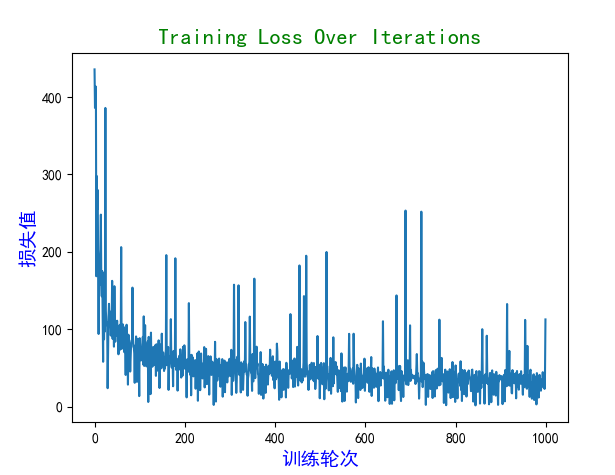
②学习率动态设置。本文学习率全程不变，可以调整为随着迭代次数的增加，学习率逐渐减小，防止错过最低点，但是学习率过低也可能会导致收敛速度慢、陷入局部最优、容易受到噪声污染。

完整代码与参考

        一般梯度下降和小批量梯度下降的源码在github项目里的train.py和train1.py。由于是虚拟环境所有我只上传了源码文件，没有上传项目文件。有帮助点个赞，有问题留言区一起探讨，非常感谢。

https://github.com/lovesuger/Boston-Housing-Price-Prediction.git

 

 

# 深度学习 # 人工智能
Logo
DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

cover

KingbaseES数据库：医疗信创潮涌沅江，国产化信创打造医疗新质生产力

avatar DAMO开发者矩阵
cover

告别迁移焦虑：金仓KDMS V4带你轻松搞定数据库国产化替代

avatar DAMO开发者矩阵
cover

KingbaseES数据库在常德二院全栈国产化信创中产生新质生产力,医疗信创的部署如何实现，如何操作？

avatar DAMO开发者矩阵