👉 代码获取和项目文档

任务介绍

MIT6.830的lab5中，我们将实现 B+ 树索引以进行高效查找和范围扫描。

项目已经提供实现树结构所需的所有低级代码。我们所要做的是实现搜索、拆分页面、在页面之间重新分配元组以及合并页面。

主要任务就是：

• 实现B+树的搜索，根据给定的key查找适当的页节点；
• 实现内部节点、页节点的拆分，当页面中key的数量大于n-1时，对页面进行拆分；
• 实现节点的重新分配，当删除key后如果页面中key的数量小于m/2 时，从其兄弟节点“窃取”一个key；
• 实现节点的合并，当删除key后如果页面中key的数量小于m/2 时，且兄弟节点也只有m/2个key，则将两个节点合并。

B+树

基本介绍

B+树是B-树的变体，也是一颗多路搜索树。一棵n阶的B+树主要有这些特点：

• 每个结点至多有n个子女;
• 非根节点关键值个数范围：n/2(取上界) <= k <= n-1
• 相邻叶子节点是通过指针连起来的，并且是关键字大小排序的。

一颗3阶的B+树如下：

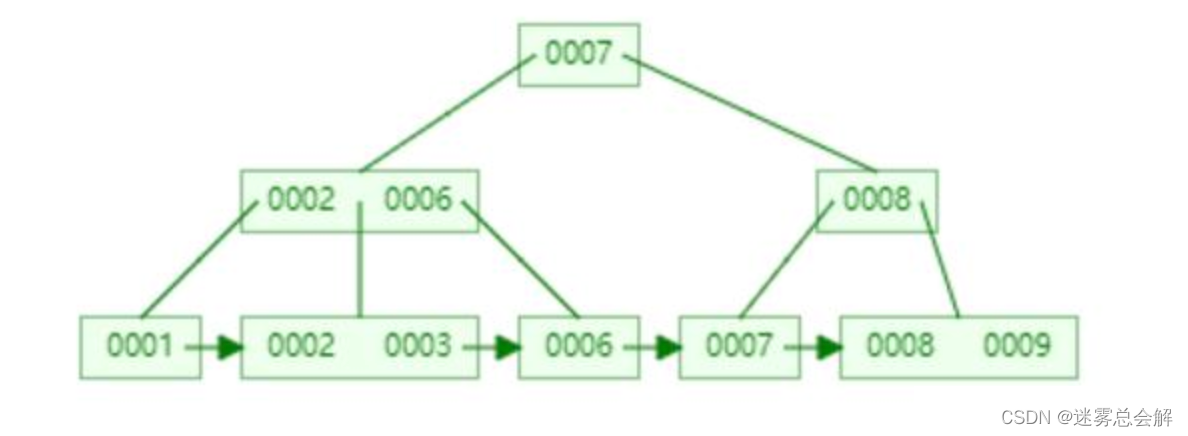
• B+树内部节点是不保存数据的，只作索引作用，它的叶子节点才保存数据；
• B+树相邻的叶子节点之间是通过链表指针连起来的；
• B+树中，内部节点与其父节点的key值不能重复，页节点与其父节点的key值可以重复。

查询

B+树的数据只存储在叶子节点，内部节点值存储索引，通过索引找到相应的叶子节点进行查询

（1）B+树的单值查询
当查询key=70的节点时，首先从读取根节点，判断得key<75；然后读取根节点的左孩子节点，将70依次与左孩子节点中的值进行比较，判断得key>66；则读取66的右孩子节点，key存储于该叶节点中，读取其中的数据。

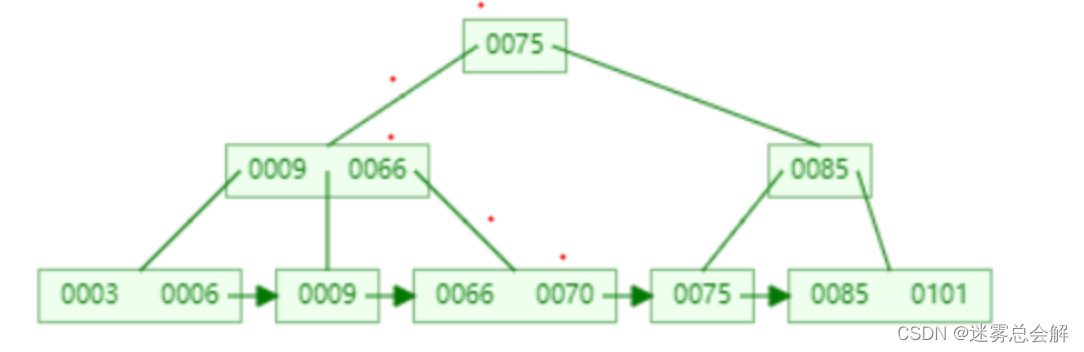
（2）B+树的范围查询

当要读取[68,100]范围内的数据时，首先找到第一个大于等于68的节点，然后在叶节点中向后遍历。

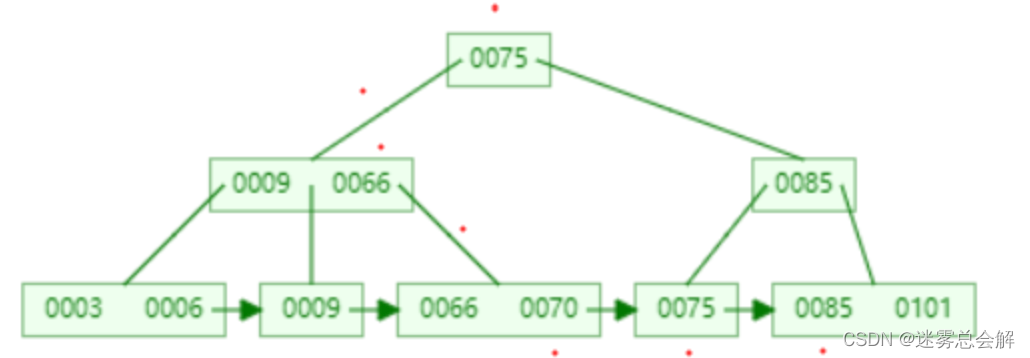
插入

B+树的插入是从叶子节点中进行的，找到要插入的叶子结点，将数据插入。然后根据插入后叶节点中key的数量进行不同的处理。

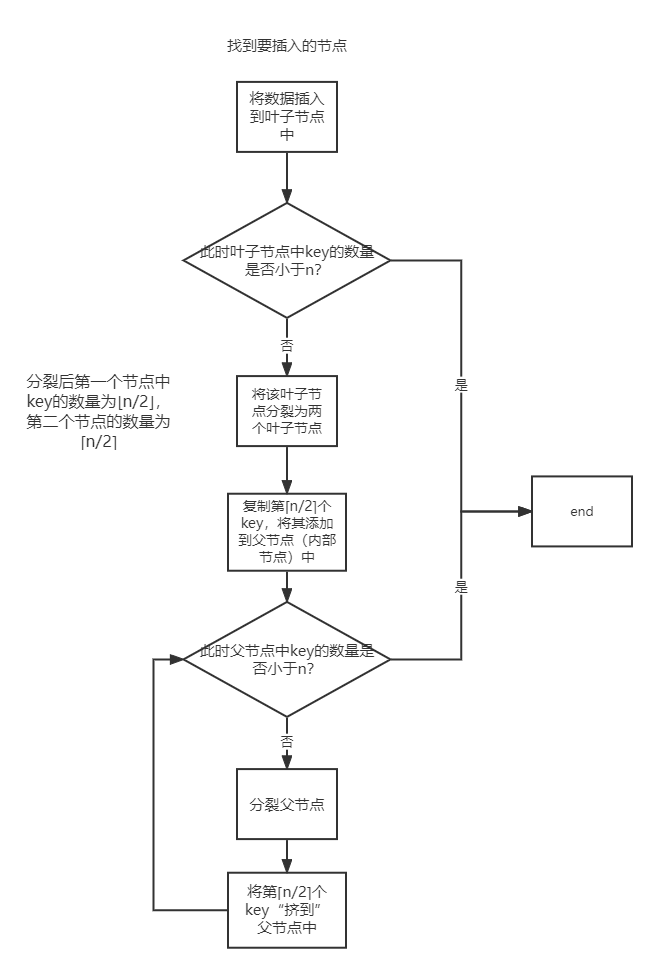
分裂叶节点和分裂内节点的情况是不同的。分裂叶节点时，节点中的key值复制到父节点中（即叶节点和内部节点可以有相同的值）

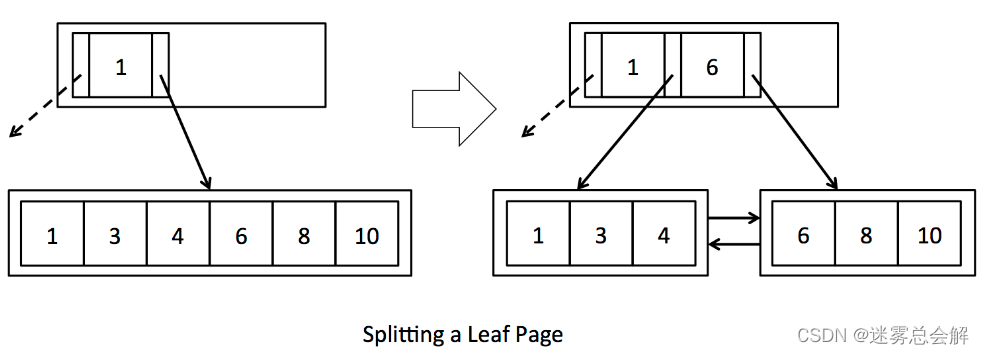
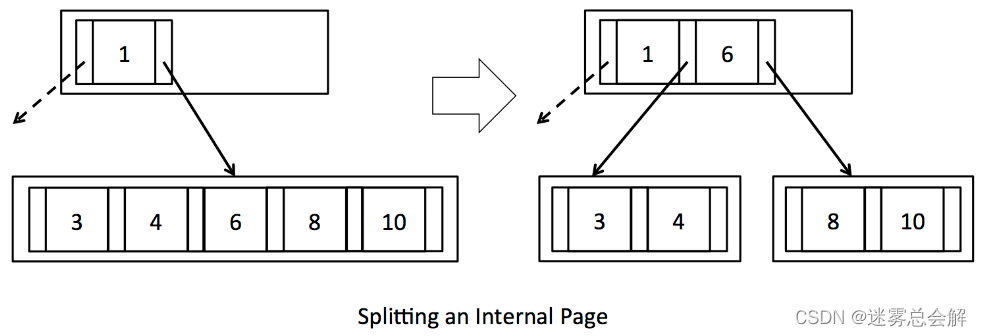
分裂内部节点时，是将节点中的key值“挤到”父节点中（即内部节点之间的key值不能重复）

删除

设：kyesNum = 节点中key的数量；min = ⌈n/2⌉-1 节点能容纳key的最小值，keysNum<min时该节点要进行合并或者“窃取”的操作；max = n-1

7阶B+树，min = 3

（1）叶子节点

keysNum < min ，兄弟节点的keys > min，从兄弟节点处“窃取”key：

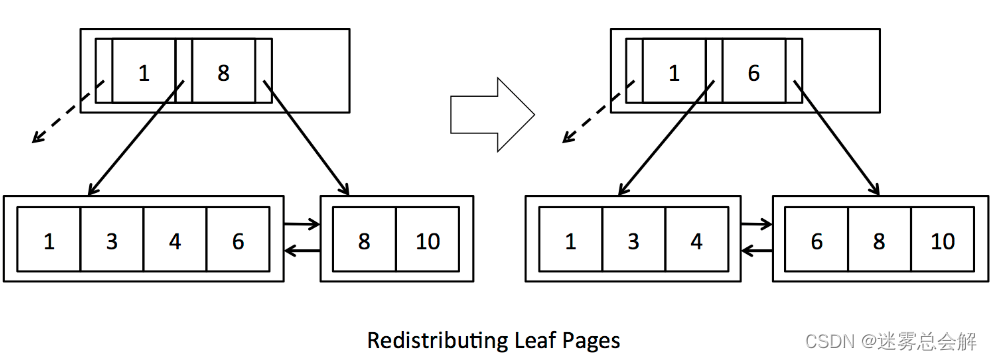
keysNum < min ，兄弟节点的keys = min，与兄弟节点合并：

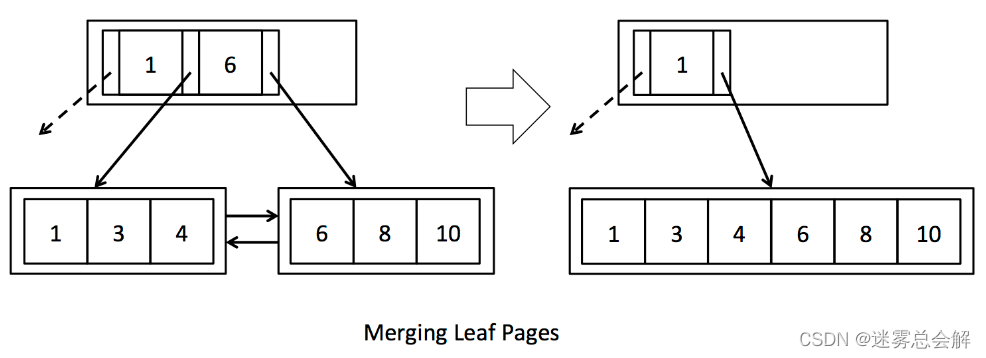
（2）内部节点

keysNum < min ，兄弟节点的keys > min，从兄弟节点处“窃取”key：

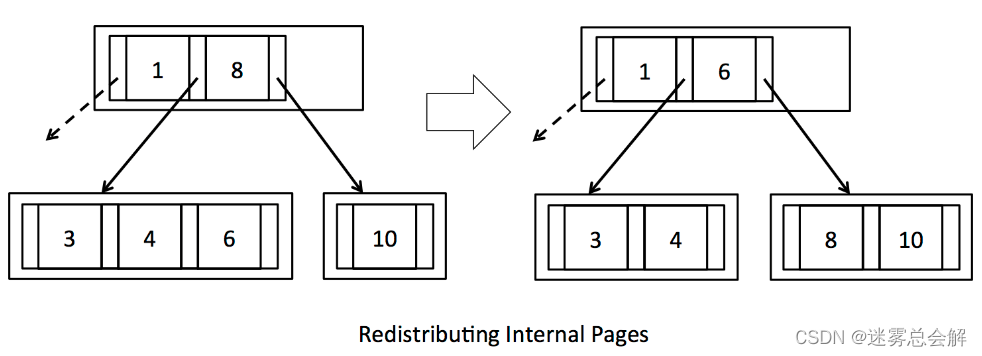
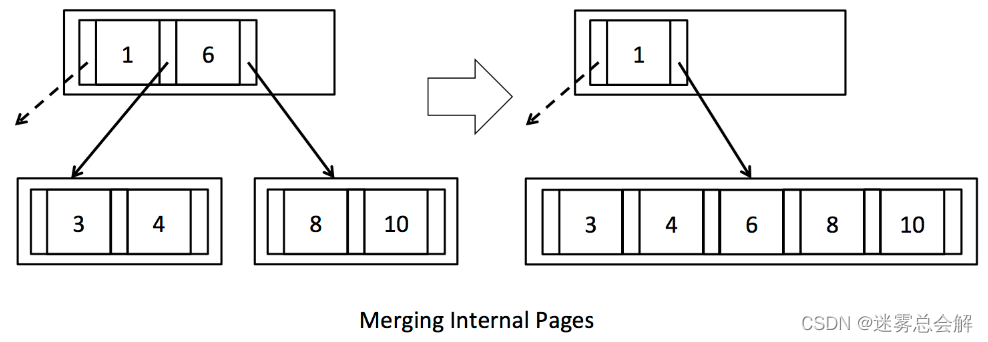
keysNum < min ，兄弟节点的keys = min，与兄弟节点合并：

基本源码介绍

在本lab中，有些基本的类已经给出了，我们只需要调用即可，但这些类，我们也要搞清楚其中的关系。

为方便起见，我们在 BTreePage.java 中创建了一个抽象类，其中包含叶页和内部页共有的代码。此外，标题页在 BTreeHeaderPage.java 中实现，并跟踪文件中的哪些页面正在使用中。最后，每个 BTreeFile 的开头都有一个页面，它指向树的根页面和第一个标题页面。这个单例页面在 BTreeRootPtrPage.java 中实现。熟悉这些类的接口，尤其是BTreePage、BTreeInternalPage 和BTreeLeafPage。您将需要在 B+Tree 的实现中使用这些类。

除了我们要实现的BTreeFile之外，主要就是：BTreePageId、BTreePage、BTreeInternalPage、 BTreeLeafPage、 BTreeHeaderPage、BTreeRootPtrPage、BTreeEntry。

（1）BTreePageId

public final static int ROOT_PTR = 0;
public final static int INTERNAL = 1;
public final static int LEAF = 2;
public final static int HEADER = 3;

private final int tableId; //该page所在的的table id
private final int pgNo;    //该page所在page的序号（table中的第几个页）
private final int pgcateg;  //用于标识BTreePage的类型，也就是ROOT_PTR、INTERNAL、LEAF、HEADER这四种类型

和在前面lab中的HeapPage一样，每一个BTreePage也都会有一个BTreePageId。

注意下ROOT_PTR、INTERNAL、LEAF、HEADER这四种类型：

• ROOT_PTR是一个指向root节点的指针；
• INTERNAL和LEAF是一棵B+树中包含的节点；
• HEADER主要是标记页的使用情况。

（2）BTreePage

// 脏页标记和事务id
protected volatile boolean dirty = false;
protected volatile TransactionId dirtier = null;

// 索引的大小，也就是每一个指针的大小
// 以页节点为例，每一个页节点都有三个索引指针：left sibling pointer, right sibling pointer, parent pointer
protected final static int INDEX_SIZE = Type.INT_TYPE.getLen();

protected final BTreePageId pid; //当前节点的BTreePageId
protected final TupleDesc td;  //当前节点的tuple元数据
protected final int keyField;  //索引的关键字字段下标

//当前page的父page，如果是根节点那么就是0
protected int parent; // parent is always internal node or 0 for root node
// 存储旧的数据，oldDataLock是用于并发synchronized的锁
protected byte[] oldData;
protected final Byte oldDataLock= (byte) 0;

这是一个抽象类，其中包含BTreeInternalPage和BTreeLeafPage共有的代码。

（3）BTreeInternalPage(继承BTreePage)

private final byte[] header; //记录slot的占用情况
private final Field[] keys;  //存储key的数组
private final int[] children;  //存储page的序号，用于获取左孩子、右孩子的BTreePageId
private final int numSlots;  //不是key的数量，而是内部节点中能存储的指针的数量（即n，内部节点中最多能存储key的数量为n-1）

private int childCategory;  //孩子节点的类型（内部节点或叶节点）

其实内部节点可以看成保存着一个个BTreeEntry，内部节点对key的查找、插入、删除、迭代，都是以entry为单位的。通过BTreeEntry可以获取key、LeftChild、RightChild这三种信息，然后存入相应数组中。

（4）BTreeLeafPage(继承BTreePage)

private final byte[] header;  //记录slot的占用情况
private final Tuple[] tuples;  //存储该page的所有tuple
private final int numSlots;  //叶节点中能存储的tuple数量（即n-1）

// 页节点的双向链表结构
private int leftSibling; //左兄弟的pageNo，用于获取左兄弟的BTreePageId，为0则没有左兄弟
private int rightSibling; //右兄弟的pageNo，用于获取右兄弟的BTreePageId，为0则没有右兄弟

叶节点和内部节点不一样的地方在于，其保存的是一个个真正的数据，也就是保存着一个个Tuple。还有就是其的链表结构用于顺序查找。

（5）BTreeRootPtrPage

//这个page的大小
public final static int PAGE_SIZE = 9; 

// 脏页标记和事务id
private boolean dirty = false;
private TransactionId dirtier = null;

// 当前节点的BTreePageId
private final BTreePageId pid;

private int root; //保存当前根节点的pageNo
private int rootCategory;  //保存当前根节点的类型，INTERNAL或LEAF，当只有一个节点时，就是LEAF
private int header;  //保存当前header页的pageNo

private byte[] oldData;  //存储旧的数据

（6）BTreeHeaderPage

// 脏页标记和事务id
private volatile boolean dirty = false;
private volatile TransactionId dirtier = null;

// 索引的大小，也就是每一个指针的大小
final static int INDEX_SIZE = Type.INT_TYPE.getLen();

final BTreePageId pid;  //当前节点的BTreePageId
final byte[] header;  //记录每一个page的使用情况，对应一个个pageNo
final int numSlots;   //记录能存储的page使用情况数量

private int nextPage; // 下一个header page的pageNo，如果是最后一个，就是0
private int prevPage; // 上一个header page的pageNo，如果是第一个，就是0

// 存储旧的数据，oldDataLock是用于并发synchronized的锁
byte[] oldData;
private final Byte oldDataLock= (byte) 0;

这个page其实就和INTERNAL和LEAF中的byte[] header作用类似，就是当做一种标记记录，来记录每一个pageNo的使用情况，当删除一页时，就可以调用BTreeFile.setEmptyPage()函数，进而调用BTreeHeaderPage.markSlotUsed()函数将header中指定的pageNo设置为unused。

（7）BTreeEntry

/**
* The key of this entry
* */
private Field key;  //内部节点中的key

/**
* The left child page id
* */
private BTreePageId leftChild;  //左孩子的BTreePageId

/**
* The right child page id
* */
private BTreePageId rightChild;  //右孩子的BTreePageId

/**
* The record id of this entry
* */
private RecordId rid; // 标识该entry所在的位置。（即该entry是哪个page中的）

内部节点中的entry，内部节点对key的查找、插入、删除、迭代，都是以entry为单位的。

来张图来直观的看一下：

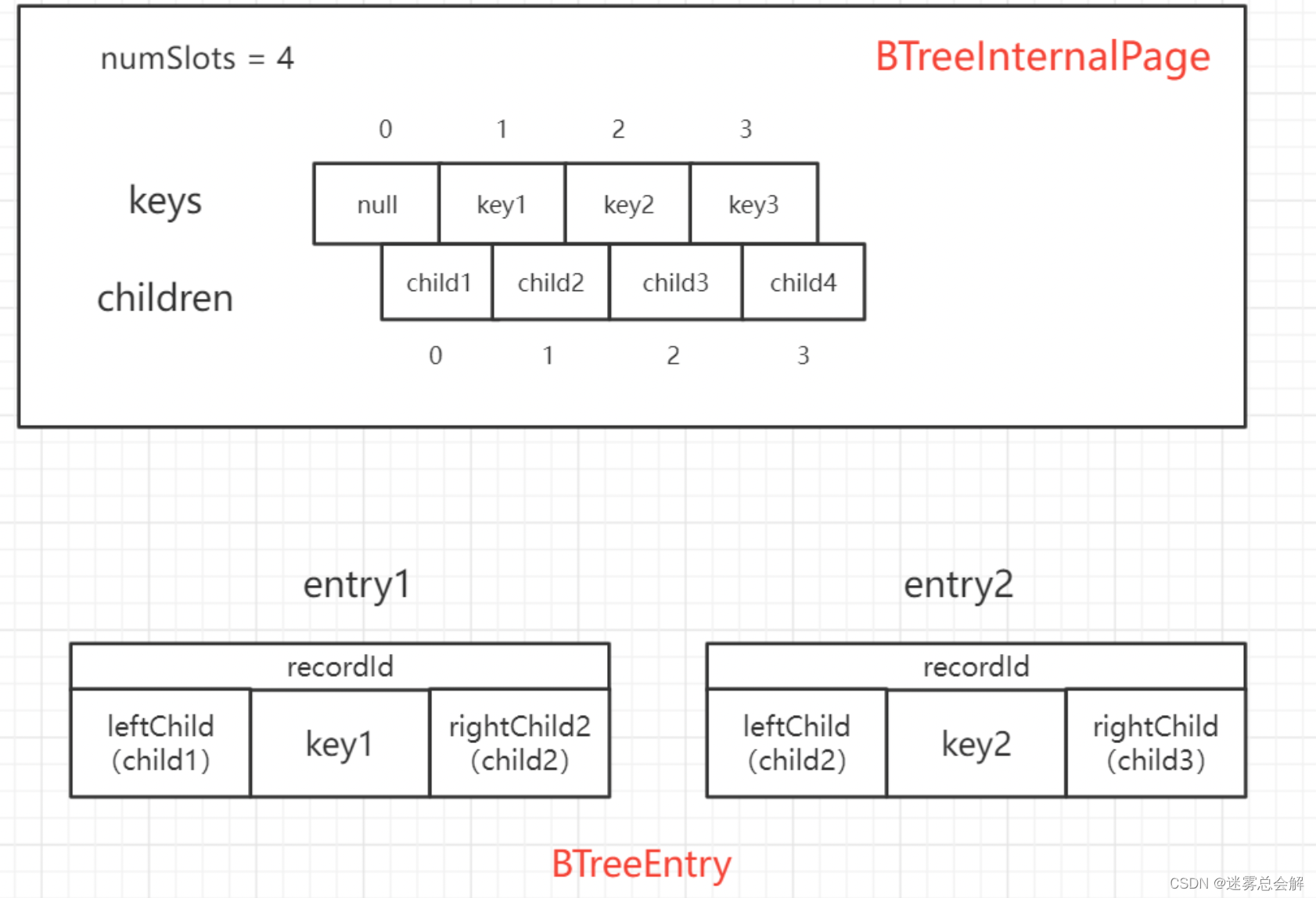
BTreeInternalPage底层页面并不存储BTreeEntry，而是存储n-1个key和n个指向子节点的指针（子页的pageNo，父页与子页同处一个table中，知道子页的pageNo就能获取到子页）。

exercise 1 - Search(BTreeFile.findLeafPage())

这个exercise主要就是实现BTreeFile中的findLeafPage()方法，实现B+树的查询。

注意这是一个递归函数，在B+树中查找可能包含字段 f 的叶节点。它使用只读权限锁定叶节点路径上的所有内部节点，并使用权限perm锁定叶节点。如果f为null，它将查找最左边的叶节点，用于迭代器。

private BTreeLeafPage findLeafPage(TransactionId tid, Map<PageId, Page> dirtypages, BTreePageId pid, Permissions perm,
                                   Field f)
    throws DbException, TransactionAbortedException {
    // some code goes here
    //1. 如果是叶子节点，直接返回
    if(pid.pgcateg() == BTreePageId.LEAF){
        return (BTreeLeafPage) getPage(tid,dirtypages,pid,perm);
    }
    BTreeInternalPage page = (BTreeInternalPage) getPage(tid,dirtypages,pid,perm);
    Iterator<BTreeEntry> iterator = page.iterator();
    //2. 如果filed为空，找到最左边的节点
    if(f==null){
        if(iterator.hasNext()){
            return findLeafPage(tid,dirtypages,iterator.next().getLeftChild(),perm,f);
        }
        return null;
    }

    BTreeEntry next = null;
    //3. 否则，内部节点查找符合条件的entry，并递归查找
    while(iterator.hasNext()){
        next =  iterator.next();
        Field key = next.getKey();
        //当有重复值的时候 节点分裂有可能一半在左边一半在右边，所以是小于等于
        if(f.compare(Op.LESS_THAN_OR_EQ,key)){
            return findLeafPage(tid,dirtypages,next.getLeftChild(),perm,f);
        }
    }

    //最后一个entry的右子节点
    if(next!=null){
        return findLeafPage(tid,dirtypages,next.getRightChild(),perm,f);
    }

    return null;
}

注意一下dirtypages：当创建新page或更改page中的数据、指针时，需要将其添加到dirtypages中。

主要判断步骤如下：

• 如果当前的节点就是叶节点了，那么直接返回，这里的叶节点要么是只有一个根节点，要么是进行递归所找到的叶节点；
• 如果filed为空，则递归找到最左边的节点，用于迭代器；
• 否则，就在当前这个内部节点进行查找，判断关键字的大小，从而进行下一步的递归。

getPage：调用getPage（）获取page时，将检查页面是否已经存储在本地缓存dirtypage中，如果不再，则调用BufferPool.getPage去获取。getPage（）如果使用读写权限获取页面，也会将页面添加到dirtypages缓存中，因为它们可能很快就会被弄脏。这种方法的一个优点是，如果在一个元组插入或删除过程中多次访问相同的页面，它可以防止更新丢失。

exercise 2 - Insert(Splitting Pages)

当我们进行插入Tuple时，可能会将数据插入到一个已经存满了Tuple的叶节点中，这就需要将该叶节点进行拆分，并将所有Tuple平均分配到两个page中(一半留在该page，一半放入另一个page)。

每次叶节点分裂时，都需要将第一页的最后一个元组对应的新条目添加到父节点。有时，内部节点也可能已满，无法接受新条目。在这种情况下，父级应该拆分并向其父级添加一个新条目。这可能会导致递归拆分并最终创建新的根节点。

而基于上诉思想，insertTuple并不需要我们完成，我们要做的任务是完成两个分裂函数：

• splitLeafPage()：进行叶节点的拆分；
• splitInternalPage()：进行内部节点的拆分。

（1）splitLeafPage

当页节点中元组数量等于n时，将其拆分成两个页节点。返回插入tuple所在的page。

public BTreeLeafPage splitLeafPage(TransactionId tid, Map<PageId, Page> dirtypages, BTreeLeafPage page, Field field)
    throws DbException, IOException, TransactionAbortedException {
    // some code goes here
    //
    // Split the leaf page by adding a new page on the right of the existing
    // page and moving half of the tuples to the new page.  Copy the middle key up
    // into the parent page, and recursively split the parent as needed to accommodate
    // the new entry.  getParentWithEmtpySlots() will be useful here.  Don't forget to update
    // the sibling pointers of all the affected leaf pages.  Return the page into which a
    // tuple with the given key field should be inserted.
    //1. 将当前page的后半部分放入新page
    int half = page.getNumTuples() / 2;
    BTreeLeafPage newPage = (BTreeLeafPage) getEmptyPage(tid, dirtypages, BTreePageId.LEAF);
    Iterator<Tuple> iterator = page.reverseIterator();
    while (iterator.hasNext() && half > 0) {
        Tuple next = iterator.next();
        //这里要先删除在插入，就很坑
        page.deleteTuple(next);
        newPage.insertTuple(next);
        half--;
    }
    //2. 获取当前要插入的父节点，并插入新节点
    Tuple up = iterator.next();
    BTreeInternalPage parentPage = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), field);
    BTreeEntry insetEntry = new BTreeEntry(up.getField(keyField), page.getId(), newPage.getId());
    parentPage.insertEntry(insetEntry);
    //3. 设置节点间的关系
    // page newPage rightSibling
    if (page.getRightSiblingId() != null) {
        BTreeLeafPage right = (BTreeLeafPage) getPage(tid, dirtypages, page.getRightSiblingId(), Permissions.READ_WRITE);
        right.setLeftSiblingId(newPage.getId());
        dirtypages.put(right.getId(),right);
    }
    newPage.setRightSiblingId(page.getRightSiblingId());
    newPage.setLeftSiblingId(page.getId());
    page.setRightSiblingId(newPage.getId());

    //4. 增加脏页
    dirtypages.put(parentPage.getId(),parentPage);
    dirtypages.put(page.getId(),page);
    dirtypages.put(newPage.getId(),newPage);

    //5. 返回要插入field的页
    if (field.compare(Op.GREATER_THAN_OR_EQ, up.getField(keyField))) {
        return newPage;
    }
    return page;

}

1. 将当前page的后半部分放入新page。通过getEmptyPage创建一个newPage，将当前page中后一半的tuple插入到newPage中。插入时应该先从page中删除tuple，然后再插入到newPage。（newRightPage插入tuple后会给其赋值新的recordId，page删除tuple时根据其recordId进行查找然后删除，而page无法定位到被赋值了新recordId的tuple，则无法将其删除）；
2. 获取当前要插入的父节点，并插入新节点。也就是将分裂后的page的最后一个tuple关键字形成一个entry并插入到父结点中。
3. 设置节点间的关系。
   • 如果当前page有右兄弟right，将right左兄弟的指针指向newPage，并将right添加到dirtypages中；
   • 将newPage的左兄弟指针指向page，newPage的右兄弟指针指向page的右兄弟，将page的右兄弟指针指向newPage；
   • 设置page和newPage的父节点；
4. 将page、newPage、parentPage添加到dirtypages中。
5. 返回field所在的页（page或newPage）。

getParentWithEmptySlots() 函数是获取一个父结点，并且这个父结点能够插入一个entry。因此这个函数中，可能会涉及内部节点的分裂。

（2）BTreeInternalPage

实现与splitLeafPage类似，区别是分裂之后要将中间的key“挤到” 父节点中去。

public BTreeInternalPage splitInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
                                           BTreeInternalPage page, Field field) 
    throws DbException, IOException, TransactionAbortedException {
    // some code goes here
    //
    // Split the internal page by adding a new page on the right of the existing
    // page and moving half of the entries to the new page.  Push the middle key up
    // into the parent page, and recursively split the parent as needed to accommodate
    // the new entry.  getParentWithEmtpySlots() will be useful here.  Don't forget to update
    // the parent pointers of all the children moving to the new page.  updateParentPointers()
    // will be useful here.  Return the page into which an entry with the given key field
    // should be inserted.
    //1. 将当前page的后半部分放入新page
    int half = page.getNumEntries()/2;
    BTreeInternalPage newPage = (BTreeInternalPage) getEmptyPage(tid, dirtypages, BTreePageId.INTERNAL);
    Iterator<BTreeEntry> iterator = page.reverseIterator();
    while(iterator.hasNext() && half>0){
        BTreeEntry next = iterator.next();
        page.deleteKeyAndRightChild(next);
        newPage.insertEntry(next);
        half--;
    }
    //2. 分裂完，中间的entry插入父节点。注意up节点要在原page中删除，并设置左右子节点。
    BTreeEntry up = iterator.next();
    page.deleteKeyAndRightChild(up);
    up.setLeftChild(page.getId());
    up.setRightChild(newPage.getId());
    //这里父节点可能还会分裂获取
    BTreeInternalPage parentPage = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), field);
    parentPage.insertEntry(up);
    page.setParentId(parentPage.getId());
    newPage.setParentId(parentPage.getId());

    //3. 设置newPage子节点的父节点指向
    updateParentPointers(tid,dirtypages,newPage);

    //4. 增加脏页
    dirtypages.put(parentPage.getId(),parentPage);
    dirtypages.put(newPage.getId(),newPage);
    dirtypages.put(page.getId(),page);
    //5. 返回要插入field的页
    if (field.compare(Op.GREATER_THAN_OR_EQ, up.getKey())) {
        return newPage;
    }
    return page;
}

1. 将当前page的后半部分放入新page；
2. 分配完entry后，选出page中最大的entry，将其从page中删除，并将该entry的左孩子指针指向page，右孩子指针指向newPage，获取父节点parent，将该entry添加到父节点中（实现将中间的key“挤到”父节点中）；
3. 将父节点parent、page、newPage添加到dirtypages中，并更新它们孩子节点的父指针；
4. 返回field所在的页（page或newPage）。

exercise 3 - Delete(Redistributing pages)

删除又是B+树的一个难点，核心在于一个节点被删到小于半满的时候，要么从（丰满的）兄弟那窃取一个元素，要么和另一个也小于半满的（苗条的）兄弟合并。而合并又会导致父节点中的划分元素被删除，运气好的时候父节点又会因为划分元素被删除了，而变成小于半满的苗条状态，然后又是要么从兄弟那窃取一个，要么和不够丰满的兄弟合并。而合并又导致他（父节点）的父节点的划分元素被删除……然后就这么在树上递归了，运气好的话能把Root节点给删了，也就是整个B+树的层数减一。

而在exercise 3中主要是实现三个和窃取有关的函数：

• stealFromLeafPage()：叶节点从左/右节点窃取tuple；
• stealFromLeftInternalPage()：内部节点从左内部节点窃取entry；
• stealFromRightInternalPage()：内部节点从右内部节点窃取entry。

（1）stealFromLeafPage

public void stealFromLeafPage(BTreeLeafPage page, BTreeLeafPage sibling,
                              BTreeInternalPage parent, BTreeEntry entry, boolean isRightSibling) throws DbException {
    // some code goes here
    //
    // Move some of the tuples from the sibling to the page so
    // that the tuples are evenly distributed. Be sure to update
    // the corresponding parent entry.
    //1. 获取要窃取的tuple个数
    int stealNum = ((page.getNumTuples()+sibling.getNumTuples())/2) - page.getNumTuples();
    if(stealNum<=0){
        return;
    }
    //2. 判断是从左还是右节点窃取，并获取迭代器
    Iterator<Tuple> tupleIterator;
    if(isRightSibling){
        tupleIterator = sibling.iterator();
    }else{
        tupleIterator = sibling.reverseIterator();
    }
    //3. 进行窃取
    Tuple next = null;
    while(stealNum>0){
        next = tupleIterator.next();
        sibling.deleteTuple(next);
        page.insertTuple(next);
        stealNum--;
    }
    //4. 新建一个entry插入父节点
    if(isRightSibling){
        entry.setKey(tupleIterator.next().getField(keyField));
    }else{
        entry.setKey(next.getField(keyField));
    }
    parent.updateEntry(entry);
}

1. 计算要窃取的tuple数量；
2. 根据传入的参数isRightSibling确定是从左兄弟中“窃取”，还是从右兄弟中“窃取”；
3. 进行tuple窃取，主要就是将兄弟节点的tuple删除，然后插入该节点；
4. 参数entry是父节点中指向page和其兄弟节点的entry，将entry的key更改为两个中右方节点的第一个tuple的关键字。

（2）stealFromLeftInternalPage

public void stealFromLeftInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
                                      BTreeInternalPage page, BTreeInternalPage leftSibling, BTreeInternalPage parent,
                                      BTreeEntry parentEntry) throws DbException, TransactionAbortedException {
    // some code goes here
    // Move some of the entries from the left sibling to the page so
    // that the entries are evenly distributed. Be sure to update
    // the corresponding parent entry. Be sure to update the parent
    // pointers of all children in the entries that were moved.
    //1. 获取要窃取的tuple个数
    int stealNum = (page.getNumEntries()+leftSibling.getNumEntries())/2 - page.getNumEntries();
    if(stealNum<=0){
        return;
    }
    //2. 获取迭代器和节点
    Iterator<BTreeEntry> leftIterator = leftSibling.reverseIterator();
    Iterator<BTreeEntry> pageIterator = page.iterator();
    BTreeEntry leftLastEntry = leftIterator.next();
    BTreeEntry pageFirstEntry = pageIterator.next();
    //3. 先将父节点中的中间entry插入page
    BTreeEntry midEntry = new BTreeEntry(parentEntry.getKey(), leftLastEntry.getRightChild(), pageFirstEntry.getLeftChild());
    page.insertEntry(midEntry);
    stealNum--;

    //4. 再插入左节点中的entry
    while(stealNum>0){
        leftSibling.deleteKeyAndRightChild(leftLastEntry);
        page.insertEntry(leftLastEntry);
        stealNum--;
        leftLastEntry = leftIterator.next();
    }

    //5. 将左节点最大的entry插入到父节点
    leftSibling.deleteKeyAndRightChild(leftLastEntry);
    parentEntry.setKey(leftLastEntry.getKey());
    parent.updateEntry(parentEntry);

    //6. 设置newPage子节点的父节点指向
    updateParentPointers(tid,dirtypages,page);

    //7. 增加脏页
    dirtypages.put(leftSibling.getId(),leftSibling);
    dirtypages.put(page.getId(),page);
    dirtypages.put(parent.getId(),parent);
}

1. 根据page及其左兄弟中key的数量，确定从其做兄弟中“窃取”几个key；
2. 因为内部节点与其父节点中的key值没有重复，迁移key的时候也需要将父节点中的key移动到page中。
3. 将page左兄弟节点中的key平均分配给page；
4. 分配之后，将page左兄弟节点中最大的key“挤到”父节点中；
5. 更新newPage子节点的父节点指向；
6. 增加脏页。

（3）stealFromRightInternalPage

public void stealFromRightInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
                                       BTreeInternalPage page, BTreeInternalPage rightSibling, BTreeInternalPage parent,
                                       BTreeEntry parentEntry) throws DbException, TransactionAbortedException {
    // some code goes here
    // Move some of the entries from the right sibling to the page so
    // that the entries are evenly distributed. Be sure to update
    // the corresponding parent entry. Be sure to update the parent
    // pointers of all children in the entries that were moved.
    //1. 获取要窃取的tuple个数
    int stealNum = (page.getNumEntries()+rightSibling.getNumEntries())/2 - page.getNumEntries();
    if(stealNum<=0){
        return;
    }
    //2. 获取迭代器和节点
    Iterator<BTreeEntry> rightIterator = rightSibling.iterator();
    Iterator<BTreeEntry> pageIterator = page.reverseIterator();
    BTreeEntry rightFirstEntry = rightIterator.next();
    BTreeEntry pageLastEntry = pageIterator.next();
    //3. 先将父节点中的中间entry插入page
    BTreeEntry midEntry = new BTreeEntry(parentEntry.getKey(), pageLastEntry.getRightChild(), rightFirstEntry.getLeftChild());
    page.insertEntry(midEntry);
    stealNum--;

    //4. 再插入右节点中的entry
    while(stealNum>0){
        rightSibling.deleteKeyAndRightChild(rightFirstEntry);
        page.insertEntry(pageLastEntry);
        stealNum--;
        rightFirstEntry = rightIterator.next();
    }

    //5. 将右节点最小的entry插入到父节点
    rightSibling.deleteKeyAndRightChild(rightFirstEntry);
    parentEntry.setKey(rightFirstEntry.getKey());
    parent.updateEntry(parentEntry);

    //6. 设置newPage子节点的父节点指向
    updateParentPointers(tid,dirtypages,page);

    //7. 增加脏页
    dirtypages.put(rightSibling.getId(),rightSibling);
    dirtypages.put(page.getId(),page);
    dirtypages.put(parent.getId(),parent);
}

1. 根据page及其右兄弟中key的数量，确定从其做兄弟中“窃取”几个key；
2. 因为内部节点与其父节点中的key值没有重复，迁移key的时候也需要将父节点中的key移动到page中。
3. 将page右兄弟节点中的key平均分配给page；
4. 分配之后，将page右兄弟节点中最大的key“挤到”父节点中；
5. 更新newPage子节点的父节点指向；
6. 增加脏页。

exercise 4 - Delete(Merging pages)

在exercise 4中主要是实现两个和page合并有关的函数：

• mergeLeafPages：删除元组时如果同级也处于最小占用率，则两个叶子节点合并，并从父级中删除指向两个page的entry，因此父结点可能也会合并；
• mergeInternalPages：叶子节点进行合并时，会删除内部节点的entry，而这可能会造成内部节点的合并

（1）mergeLeafPages

public void mergeLeafPages(TransactionId tid, Map<PageId, Page> dirtypages,
                           BTreeLeafPage leftPage, BTreeLeafPage rightPage, BTreeInternalPage parent, BTreeEntry parentEntry) 
    throws DbException, IOException, TransactionAbortedException {

    // some code goes here
    //
    // Move all the tuples from the right page to the left page, update
    // the sibling pointers, and make the right page available for reuse.
    // Delete the entry in the parent corresponding to the two pages that are merging -
    // deleteParentEntry() will be useful here
    //1. 设置右兄弟节点
    leftPage.setRightSiblingId(rightPage.getRightSiblingId());
    //2. 如果右节点有右兄弟节点，就设置其左节点指向
    if(rightPage.getRightSiblingId()!=null){
        BTreeLeafPage rightSiblingPage= (BTreeLeafPage) getPage(tid, dirtypages, rightPage.getRightSiblingId(), Permissions.READ_WRITE);
        rightSiblingPage.setLeftSiblingId(leftPage.getId());
        dirtypages.put(rightSiblingPage.getId(),rightSiblingPage);
    }
    //3. 进行合并
    Iterator<Tuple> iterator = rightPage.iterator();
    while(iterator.hasNext()){
        Tuple next = iterator.next();
        rightPage.deleteTuple(next);
        leftPage.insertTuple(next);
    }
    //4. 设置空page并删除父结点的entry
    setEmptyPage(tid,dirtypages,rightPage.getId().getPageNumber());
    deleteParentEntry(tid,dirtypages,leftPage,parent,parentEntry);
    //5. 增加脏页
    dirtypages.remove(rightPage.getId());
    dirtypages.put(leftPage.getId(),leftPage);
    dirtypages.put(parent.getId(),parent);
}

1. 设置右兄弟节点；
2. 判断右节点是否有右兄弟节点，如果有，就设置其左节点指向；
3. 进行节点的合并；
4. 调用setEmptyPage方法将rightPage在header标记为空，调用deleteParentEntry方法，从父级中删除左右孩子指针指向leftPage和rightPage的entry；
5. 将leftPage、rightPage、parent添加到dirtypages中。

（2）mergeInternalPages

public void mergeInternalPages(TransactionId tid, Map<PageId, Page> dirtypages,
                               BTreeInternalPage leftPage, BTreeInternalPage rightPage, BTreeInternalPage parent, BTreeEntry parentEntry) 
    throws DbException, IOException, TransactionAbortedException {

    // some code goes here
    //
    // Move all the entries from the right page to the left page, update
    // the parent pointers of the children in the entries that were moved, 
    // and make the right page available for reuse
    // Delete the entry in the parent corresponding to the two pages that are merging -
    // deleteParentEntry() will be useful here
    //1. 获取两个节点的迭代器
    Iterator<BTreeEntry> leftIterator = leftPage.reverseIterator();
    Iterator<BTreeEntry> rightIterator = rightPage.iterator();
    BTreeEntry leftLastEntry = leftIterator.next();
    BTreeEntry rightFirstEntry = rightIterator.next();
    //2. 将两节点中间的父节点entry插入到左节点，并将其删除
    BTreeEntry midEntry = new BTreeEntry(parentEntry.getKey(), leftLastEntry.getRightChild(), rightFirstEntry.getLeftChild());
    leftPage.insertEntry(midEntry);
    deleteParentEntry(tid,dirtypages,leftPage,parent,parentEntry);
    //3. 插入右节点的第一个entry
    rightPage.deleteKeyAndLeftChild(rightFirstEntry);
    leftPage.insertEntry(rightFirstEntry);
    //4. 循环插入右节点的entry
    while(rightIterator.hasNext()){
        rightFirstEntry = rightIterator.next();
        rightPage.deleteKeyAndLeftChild(rightFirstEntry);
        leftPage.insertEntry(rightFirstEntry);
    }
    //5. 更新左节点的子节点的父节点指向
    updateParentPointers(tid,dirtypages,leftPage);
    //6. 设置空page
    setEmptyPage(tid,dirtypages,rightPage.getId().getPageNumber());
    //7. 增加脏页
    dirtypages.remove(rightPage.getId());
    dirtypages.put(leftPage.getId(),leftPage);
    dirtypages.put(parent.getId(),parent);
}

1. 先将父节点中的指向leftPage和rightPage的entry添加到leftPage中，并将其删除；
2. 将rightPage中的entry添加到leftPage中；
3. 更新左节点的子节点的父节点指向；
4. 设置空page；
5. 增加脏页。