OpenCV + CPP 系列（卌九）聚类与图像分割（GMM- 混合高斯模型）

文章目录GMM 简介GMM 聚类数据演示GMM 图像分割示例GMM 简介关于高斯混合模型理论：https://zhuanlan.zhihu.com/p/30483076关于高斯混合模型理论：https://wangsp.blog.csdn.net/article/details/81009717高斯混合模型 (GMM) 为关于数据的高斯分布与观测数据在总体分布中密度概率的数据分析模型。当样本数据

SongpingWang

787人浏览 · 2021-09-08 10:05:39

SongpingWang · 2021-09-08 10:05:39 发布

文章目录

GMM 简介

关于高斯混合模型理论：https://zhuanlan.zhihu.com/p/30483076
关于高斯混合模型理论：https://wangsp.blog.csdn.net/article/details/81009717
高斯混合模型 (GMM) 为关于数据的高斯分布与观测数据在总体分布中密度概率 的数据分析模型。

当样本数据 $X$ 是一维数据（Univariate）时，高斯分布遵从下方概率密度函数（Probability Density Function）：
$P(x|\theta) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$
其中 $\mu$ 为数据均值（期望）， $\sigma$ 为数据标准差（Standard deviation）。
当样本数据 X 是多维数据（Multivariate）时，高斯分布遵从下方概率密度函数：
$P(x|\theta) = \frac{1}{(2\pi)^{\frac{D}{2}}|\Sigma|^{\frac{1}{2}}}\exp \left(-\frac{(x-\mu)^T \Sigma^{-1}(x-\mu)}{2} \right)$
其中， $\mu$ 为数据均值（期望）， $\Sigma$ 为协方差（Covariance）， $D$ 为数据维度。

GMM特点

跟K-Means相比较，属于软分类
实现方法-期望最大化(E-M)
停止条件-收敛

头文件 machine_learning_all.h：

#pragma once
#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;


class Machine_learning{
public:
	void GMM_data_demo();
	void GMM_image_demo(Mat& image);
};

主函数main.cpp

#include "machine_learning_all.h"


int main(int argc, char** argv) {
	const char* input_path = "D:\\Desktop\\meinv3.png";
	Mat src = imread(input_path);
	if (src.empty()) {
		cout << "Read image failed!" << endl;
		return -1;
	}

	Machine_learning ml;
	ml.GMM_data_demo();
	ml.GMM_image_demo(src);

	imshow("src", src);
	waitKey(0);
	destroyAllWindows();
	return 0;
}

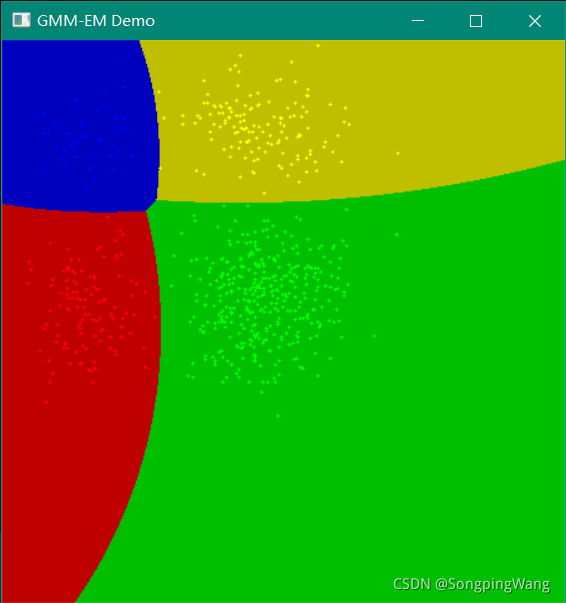
GMM 聚类数据演示

void Machine_learning::GMM_data_demo() {
	Mat img = Mat::zeros(450, 450, CV_8UC3);
	RNG rng(1233);

	Scalar colorTab[] = {
		Scalar(0,0,255),
		Scalar(0,255,0),
		Scalar(255,0,0),
		Scalar(0,255,255),
		Scalar(255,0,255),
		Scalar(255,255,0)
	};

	int numCluster = rng.uniform(2, 5);
	cout << "Number of cluster: " << numCluster << endl;

	int sampleCount = rng.uniform(500, 1000);
	Mat points(sampleCount, 2, CV_32FC1); //生成数据 (height,width)=(sampleCount,2)
	Mat labels;
	Mat centers;
	cout << "points.size():" << points.size() << endl;

	//生成随机数
	for (int k = 0; k < numCluster; k++) {
		Point center;
		center.x = rng.uniform(0, img.cols);
		center.y = rng.uniform(0, img.rows);
		Mat PointChunk = points.rowRange(
			k * sampleCount / numCluster,
			k == numCluster - 1 ? sampleCount : (k + 1) * sampleCount / numCluster
		);
		rng.fill(PointChunk, RNG::NORMAL, Scalar(center.x, center.y), Scalar(img.cols * 0.05, img.rows * 0.05));
	}
	randShuffle(points, 1, &rng);

	// 初始化模型参数
	Ptr<ml::EM> em_model = ml::EM::create();
	em_model->setClustersNumber(numCluster);
	em_model->setCovarianceMatrixType(ml::EM::COV_MAT_SPHERICAL);
	em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));
	em_model->trainEM(points, noArray(), labels, noArray());

	// 分类图像像素
	Mat sample = Mat::zeros(1, 2, CV_32FC1);
	for (int row = 0; row < img.rows; row++) {
		for (int col = 0; col < img.cols; col++) {
			sample.at<float>(0) = (float)col;
			sample.at<float>(1) = (float)row;
			int response = cvRound(em_model->predict2(sample, noArray())[1]);
			Scalar c = colorTab[response];
			circle(img, Point(col, row), 1, c * 0.75, -1);
		}
	}

	// draw the clusters(point)
	for (int i = 0; i < sampleCount; i++) {
		Point p(cvRound(points.at<float>(i, 0)), points.at<float>(i, 1));
		circle(img, p, 1, colorTab[labels.at<int>(i)], -1);
	}
	imshow("GMM-EM Demo", img);
}

在这里插入图片描述

GMM 图像分割示例

void Machine_learning::GMM_image_demo(Mat& src) {
	RNG rng(1212);
	//int numCluster = rng.uniform(2, 5);
	int numCluster = 5;
	Scalar colorTab[] = {
		Scalar(0,0,255),
		Scalar(0,255,0),
		Scalar(255,0,0),
		Scalar(0,255,255),
		Scalar(255,0,255),
		Scalar(255,255,0)
	};

	int width = src.cols;
	int height = src.rows;
	int dims = src.channels();
	int nsamples = width * height;
	Mat points(nsamples, dims, CV_64FC1);
	Mat labels;
	Mat result = Mat::zeros(src.size(), CV_8UC3);

	// 图像RGB像素数据转换为样本数据 
	int index = 0;
	for (int row = 0; row < height; row++) {
		Vec3b* bgr_ptr = src.ptr<Vec3b>(row);
		for (int col = 0; col < width; col++) {
			index = row * width + col;
			points.at<double>(index, 0) = static_cast<int>(bgr_ptr[col][0]);
			points.at<double>(index, 1) = static_cast<int>(bgr_ptr[col][1]);
			points.at<double>(index, 2) = static_cast<int>(bgr_ptr[col][2]);
		}
	}

	// EM Cluster Train
	Ptr<ml::EM> em_model = ml::EM::create();
	em_model->setClustersNumber(numCluster);
	em_model->setCovarianceMatrixType(ml::EM::COV_MAT_SPHERICAL);
	em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));
	em_model->trainEM(points, noArray(), labels, noArray());

	// 对每个像素标记颜色与显示
	Mat sample = Mat::zeros(dims, 1, CV_64FC1);
	double time = getTickCount();
	int r = 0, g = 0, b = 0;
	for (int row = 0; row < height; row++) {
		Vec3b* src_ptr = src.ptr<Vec3b>(row);
		uchar* result_ptr = result.ptr<uchar>(row);
		for (int col = 0; col < width; col++) {
			index = row * width + col;
			sample.at<double>(0) = src_ptr[col][0];
			sample.at<double>(1) = src_ptr[col][1];
			sample.at<double>(2) = src_ptr[col][2];
			int response = cvRound(em_model->predict2(sample, noArray())[1]);
			Scalar c = colorTab[response];
			*result_ptr++ = c[0];
			*result_ptr++ = c[1];
			*result_ptr++ = c[2];
		}
	}
	printf("execution time(ms) : %.2f\n", (getTickCount() - time) / getTickFrequency() * 1000);
	imshow("EM-Segmentation", result);
	imwrite("D:\\Desktop\\EM-Segmentation.png", result);
}