机器学习模型解决互为因果_学习因果模型_机器学习_weixin

机器学习模型解决互为因果

Author: Hi, I’m St John and I write blogs about modern technologies and interesting things for my personal blog stjohngrimbly.com. I’m currently interested in machine learning and causality among other things. I hope you enjoy this quick read!

作者：嗨，我是St John，我为个人博客 stjohngrimbly.com 撰写有关现代技术和有趣事物的博客 。 我目前对机器学习和因果关系感兴趣。 希望您喜欢本快速阅读！

In the last episode we developed the first tools we need to develop the theory needed to formalise interventions and counterfactual reasoning. In this article we’ll discuss how we can go about learning such a causal model from some observational data, and what constraints are required for doing this. Note, this is an active area of research and so we really don’t have all the tools yet. This should be both a cautionary note and an exciting motivation to get involved in this research! This is really when the theory of causal inference starts to get exciting, so tighten your seat-belts.

在上一集中，我们开发了我们需要的第一个工具，以发展为干预和反事实推理形式化所需的理论。在本文中，我们将讨论如何从一些观测数据中学习这种因果模型，以及进行此操作需要哪些约束。请注意，这是一个活跃的研究领域，因此我们确实还没有所有工具。这既是警告提示，也是参与该研究的令人兴奋的动力！当因果推理理论开始变得令人兴奋时，请务必系紧安全带。

可识别性 (Identifiability)

Previously, we discussed the idea that an SCM induces a joint distribution over the variables of interest. For example, the SCM C → E induces P_{C,E}. Naturally, we wonder whether we can identify, in general, whether the joint distribution came from the SCM C → E or E → C. It turns out, the graphs are not unique. In other words, structure is not identifiable from the joint distribution. Another way of phrasing this is the graph adds an additional layer of knowledge.

先前，我们讨论了SCM引起关注变量的联合分布的想法。例如，SCM C→E得出P_ {C，E}。自然地，我们想知道是否可以识别出一般的联合分布是来自SCM C→E还是E→C。事实证明，这些图不是唯一的。换句话说，无法从联合分布中识别出结构。短语的另一种表达方式是图形添加了额外的知识层。

Non-uniqueness of graph structures: For every joint distribution P_{X,Y} of two real-valued variables, there is an SCM Y = f_Y(X, N_Y), X ⟂ Y, where f_Y is a measurable function and N_Y is a real-valued noise variable.

图结构的非唯一性：对于两个实值变量的每个联合分布P_ {X，Y}，都有一个SCM Y = f_Y(X，N_Y)，X⟂Y，其中f_Y是可测量的函数，N_Y是实值噪声变量。

This proposition indicates that we can construct an SCM from a joint distribution in any direction. This is crucial to keep in mind, especially if we plan on trying to use observational data to infer causal structure.

这个命题表明我们可以从任何方向上的联合分布构造SCM。要牢记这一点至关重要，尤其是如果我们计划尝试使用观察数据来推断因果结构时，这一点尤其重要。

We are now ready to discuss some methods of identifying cause and effect with some a priori restrictions on the class of models we are using.

现在，我们准备讨论一些识别原因和结果的方法，这些方法对我们使用的模型类别具有先验限制。

加性噪声模型 (Additive Noise Models)

Our first class of model are the linear non-Gaussian acyclic models (LiNGAMs). Here we assume that the effect is a linear function of the cause up to some additive noise term, E = 𝜶C + N_E, 𝜶∈ℝ. Note, we are explicitly removing the possibility that the additive noise is Gaussian in nature. With this restrictive assumption in place, we can formulate the identifiability result we are looking for:

我们的第一类模型是线性非高斯非循环模型(LiNGAM)。在这里，我们假设影响是原因的线性函数，直到某些附加噪声项E = 𝜶C + N_E，𝜶∈ℝ。注意，我们明确地消除了加性噪声本质上是高斯的可能性。有了这个限制性假设，我们可以制定我们正在寻找的可识别性结果：

Identifiability of linear non-Gaussian models: Given the joint distribution P_{X,Y} having linear model Y = 𝜶X + N_Y, N_Y ⟂ X, with continuous random variables X, N_Y, and Y. Then there exists β∈ ℝand random variable N_X such that X = βY + N_X, N_X ⟂ Y, if and only if N_Y and X are Gaussian.

线性非高斯模型的可辨识性：给定具有线性模型Y = 𝜶X + N_Y，N_Y⟂X的联合分布P_ {X，Y}，具有连续的随机变量X，N_Y和Y。则存在β∈和随机变量N_X使得X =βY+ N_X，N_X⟂Y，当且仅当N_Y和X为高斯时。

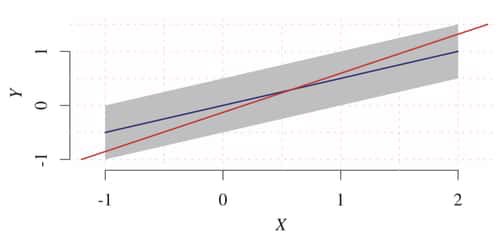
Peters provides a lucid example of this in action. Here we have uniform noise over X and a linear relationship between the variables of interest. The backwards model, shown in blue, is not valid because the noise term over X is not independent of the variable Y, violating the independence condition.

彼得斯为此提供了一个清晰的例子。在这里，我们在X上具有均匀的噪声，并且感兴趣的变量之间具有线性关系。向后模型(以蓝色显示)无效，因为X上的噪声项与变量Y无关，从而违反了独立性条件。

Interestingly enough, non-Gaussian additive noise can be applied to estimating the arrow of time from data!

有趣的是，可以将非高斯加性噪声应用于根据数据估算时间箭头！

We are now ready to extend the discussion the nonlinear additive noise models.

现在，我们准备扩展对非线性加性噪声模型的讨论。

Additive noise model (ANM): The joint distribution P_{X,Y} is said to admit an ANM from X to Y if there is a measurable function f_Y and a noise variable N_Y such that Y = F_Y(X) + N_Y, N_Y ⟂ X.

加性噪声模型(ANM)：如果存在可测量的函数f_Y和噪声变量N_Y，使得Y = F_Y(X)+ N_Y，N_Y，则说联合分布P_ {X，Y}允许从X到Y的ANM。 ⟂X.

We can extend the identifiability condition to include ANMs as well. For brevity I shall not include it. Peters, however, provides a nice description and proof sketch in chapter 4 of his book. Further extensions, such as to discrete ANMs and post-nonlinear models, are possible and described in the literature.

我们可以将可识别性条件扩展为也包括ANM。为简洁起见，我将不包括在内。然而，彼得斯在其书的第4章中提供了一个很好的描述和证明草图。可能的进一步扩展，例如离散ANM和非线性后模型，已在文献中进行了描述。

信息几何因果推理 (Information-Geometric Causal Inference)

We now turn to the idea of formalising the independence condition between P_{E|C} and P_C. Assuming the (strong) condition that Y = f(X) and X = inverse f(Y), the principle of independence of cause and mechanism simplifies to the independence between P_X and f.

现在我们来讨论使P_ {E | C}和P_C之间的独立条件形式化的想法。假设(强)条件Y = f(X)和X =逆f(Y)，原因和机制的独立性原理简化为P_X和f之间的独立性。

Avoiding the detailed mathematics for now, the results show that the ‘uncorrelatedness’ of log(f’) and p_X necessarily implies correlation between -log(f’) and p_Y. The logarithms here are used for the sake of interpretibility of the result, but it is not a necessary formulation for the result to hold.

结果暂时避免了详细的数学运算，结果表明log(f')和p_X的“不相关性”必然意味着-log(f')和p_Y之间的相关性。这里的对数是为了解释结果而使用的，但这并不是保持结果的必要公式。

It has been shown, as we shall soon come across, that the performance of semi-supervised learning methods is dependent on the causal direction. IGCI can explain this using assumptions similar to what we have just discussed.

正如我们将很快看到的那样，已经表明，半监督学习方法的性能取决于因果关系。 IGCI可以使用类似于我们刚刚讨论的假设来解释这一点。

接下来 (Next up)

With that reference to machine learning, that should satisfy for curiosity — at least temporarily. In the next session we’ll take this idea further and discuss some more theory before jumping into the problem of machine learning.

关于机器学习，至少应该暂时满足好奇心。在下一节中，我们将进一步探讨这个想法，并在跳入机器学习问题之前讨论更多理论。