【机器学习】集成学习与梯度提升决策树

本文系统介绍了集成学习方法及其核心算法，包括自举聚合(Bagging)、随机森林、AdaBoost、梯度提升决策树(GBDT)和XGBoost。主要内容涵盖：Bagging与随机森林、梯度提升算法、Python实现实验和算法评估，本文通过理论推导与实验验证相结合，全面阐述了集成学习降低方差、提升泛化能力的机制，为实际应用提供了技术参考。

2401_84149564

1540人浏览 · 2025-06-02 04:14:57

2401_84149564 · 2025-06-02 04:14:57 发布

五、Python代码实现集成学习与梯度提升决策树的实验

六、总结

一、引言

在机器学习的广阔领域中，集成学习（Ensemble Learning）犹如一座闪耀的明星，它通过组合多个基本学习器的力量，创造出远超单个模型的预测能力。梯度提升决策树融合了决策树的可解释性与梯度优化的高效性，成为了现代机器学习领域最受欢迎的算法之一。本文将详细介绍自举聚合与随机森林、集成学习器、提升算法以及Python代码实现集成学习与梯度提升决策树的实验。

二、自举聚合与随机森林

1. 自举聚合(Bagging)原理

1.1 基本概念

自举聚合(Bootstrap Aggregating，简称Bagging)是一种集成学习方法，旨在通过结合多个基学习器的预测来提高模型的稳定性和准确性。该方法由Leo Breiman于1996年提出，其核心思想是利用自助采样(Bootstrap Sampling)技术从原始训练数据中生成多个不同的训练子集，然后在每个子集上独立训练一个基学习器，最后将所有基学习器的预测结合起来。

1.2 数学形式化描述

给定训练集 $D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$ ，Bagging的过程可以表示为：

（1）自助采样：对于 $t = 1, 2, \ldots, T$ ：通过有放回抽样，从 $D$ 中随机抽取 $n$ 个样本，形成训练子集 $D_t$ 。

（2）训练基学习器：对每个训练子集 $D_t$ ，独立训练得到基学习器 $h_t(x)$ 。

（3）组合预测：

a.对于分类问题，使用投票法：

$H(x) = \arg\max_y \sum_{t=1}^T \mathbf{1}(h_t(x) = y)$

b. 对于回归问题，使用平均法：

$H(x) = \frac{1}{T}\sum_{t=1}^T h_t(x)$

其中， $T$ 是基学习器的数量， $\mathbf{1}(\cdot)$ 是指示函数。

1.3 理论基础

Bagging成功的关键在于减少了方差。具体来说，假设每个基学习器的错误期望为 $E[error] = bias^2 + var + noise$ ，当基学习器相互独立时，集成后的方差会减小为原来的 $\frac{1}{T}$ 。对于具有方差 $\sigma^2$ 的 $T$ 个独立同分布的随机变量，它们的平均值的方差为 $\frac{\sigma^2}{T}$ ，即：

$Var\left(\frac{1}{T}\sum_{t=1}^T h_t(x)\right) = \frac{1}{T^2}\sum_{t=1}^T Var(h_t(x)) = \frac{\sigma^2}{T}$

1.4 袋外估计(OOB, Out-of-Bag Estimation)

由于自助采样是有放回的，每个训练子集 $D_t$ 包含原始训练集中约63.2%的样本，剩余约36.8%的样本未被选中，称为"袋外样本"。

对于每个样例 $(x_i, y_i)$ ，可以用没有使用它训练的基学习器对它进行预测，得到的错误率称为"袋外误差"(OOB Error)，其形式化定义为：

$\epsilon_{oob} = \frac{1}{n}\sum_{i=1}^n \mathbf{1}\left(y_i \neq \arg\max_y \sum_{t:x_i \notin D_t} \mathbf{1}(h_t(x_i) = y)\right)$

OOB估计是泛化误差的无偏估计，可以用来代替交叉验证。

2. 随机森林(Random Forest)

2.1 基本概念

随机森林是Bagging的特殊情况，它使用决策树作为基学习器，并在决策树构建过程中引入了额外的随机性。随机森林同样由Leo Breiman在2001年提出，是目前最流行的集成学习方法之一。

2.2 随机森林的两层随机性

随机森林包含两层随机性：

(1) 样本随机性：与Bagging一样，通过有放回抽样生成训练子集。

(2) 特征随机性：在每个节点分裂时，不考虑所有特征，而只考虑随机选择的特征子集。

此特征随机化机制可以形式化表示为：对于每个决策树节点，从 $d$ 个特征中随机选择 $m$ 个特征（通常 $m = \sqrt{d}$ 或 $m = \log_2 d$ ），然后仅在这 $m$ 个特征中寻找最优分割点。

2.3 数学模型

假设原始特征空间维度为 $d$ ，则随机森林的构建过程为：

（1）对于 $t = 1, 2, \ldots, T$ ：

a.通过有放回抽样，从训练集 $D$ 中随机抽取 $n$ 个样本，形成训练子集 $D_t$ 。

b.在 $D_t$ 上训练一棵决策树 $h_t$ ，其中每个节点分裂时：

（a）随机选择 $m$ 个特征（ $m \ll d$ ）。

（b）在这 $m$ 个特征中找到最佳分裂特征和分裂点。

（c）按该分裂生成子节点。

（d）递归处理子节点，直到满足停止条件。

（2）最终的随机森林模型：

a.分类问题：

$H(x) = \arg\max_y \sum_{t=1}^T \mathbf{1}(h_t(x) = y)$

b.回归问题：

$H(x) = \frac{1}{T}\sum_{t=1}^T h_t(x)$

2.4 特征重要性计算

随机森林可以计算特征的重要性分数，这是其重要的优势之一。对于特征j的重要性，可以通过计算其在所有树中的平均不纯度减少量来估计：

$Imp(j) = \frac{1}{T} \sum_{t=1}^T \sum_{k \in S_j^t} \Delta I(S_{k,t})$

其中， $S_j^t$ 表示树 $t$ 中使用特征 $j$ 进行分裂的所有节点集合， $\Delta I(S_{k,t})$ 表示节点 $k$ 分裂前后的不纯度减少量。

3.优势与应用

3.1 优势

（1）减少方差：通过多次采样训练，降低了模型的方差，提高了稳定性。

（2）避免过拟合：特征的随机选择使得树之间相关性降低，减轻了过拟合。

（3）提供OOB估计：无需额外的验证集即可估计泛化误差。

（4）内置特征重要性评估：可以评估各个特征对预测的贡献。

（5）高度并行化：树之间相互独立，可以并行训练，提高效率。

（6）处理高维数据：能够处理具有大量特征的数据集。

（7）处理缺失值：对缺失值具有较强的鲁棒性。

3.2 典型应用场景

（1）分类任务：信用评分、垃圾邮件检测、疾病诊断。

（2）回归任务：房价预测、销售额预测。

（3）特征选择：通过特征重要性评估进行降维。

（4）异常检测：识别与正常模式不符的数据点。

4.自举聚合与随机森林的代码实现

4.1自定义实现Bagging类

class Bagging:
    def __init__(self, base_estimator, n_estimators=10):
        self.base_estimator = base_estimator  # 基学习器
        self.n_estimators = n_estimators  # 基学习器数量
        self.estimators = []  # 存储训练好的基学习器
        
    def fit(self, X, y):
        n_samples = X.shape[0]
        
        # 训练n_estimators个基学习器
        for _ in range(self.n_estimators):
            # 有放回抽样
            indices = np.random.choice(n_samples, n_samples, replace=True)
            X_bootstrap, y_bootstrap = X[indices], y[indices]
            
            # 克隆并训练基学习器
            estimator = clone(self.base_estimator)
            estimator.fit(X_bootstrap, y_bootstrap)
            self.estimators.append(estimator)
            
        return self
    
    def predict(self, X):
        # 收集所有基学习器的预测
        predictions = np.array([estimator.predict(X) for estimator in self.estimators])
        
        # 投票得到最终预测（适用于分类问题）
        if len(np.unique(predictions.flatten())) < 10:  # 假设小于10个唯一值为分类
            # 分类问题：多数投票
            return np.apply_along_axis(
                lambda x: np.bincount(x).argmax(),
                axis=0,
                arr=predictions)
        else:
            # 回归问题：平均值
            return np.mean(predictions, axis=0)

4.2自定义实现随机森林类

class RandomForest:
    def __init__(self, n_estimators=100, max_features='sqrt', max_depth=None):
        self.n_estimators = n_estimators
        self.max_features = max_features
        self.max_depth = max_depth
        self.trees = []
        self.oob_score_ = None
        
    def _bootstrap_sample(self, X, y):
        n_samples = X.shape[0]
        # 有放回抽样
        indices = np.random.choice(n_samples, n_samples, replace=True)
        # 记录袋外样本索引
        oob_indices = np.array([i for i in range(n_samples) if i not in np.unique(indices)])
        
        return X[indices], y[indices], oob_indices
    
    def fit(self, X, y):
        n_samples = X.shape[0]
        n_features = X.shape[1]
        
        # 确定每个节点随机选择的特征数量
        if self.max_features == 'sqrt':
            self.max_features_used = int(np.sqrt(n_features))
        elif self.max_features == 'log2':
            self.max_features_used = int(np.log2(n_features))
        elif isinstance(self.max_features, int):
            self.max_features_used = self.max_features
        else:
            self.max_features_used = n_features
            
        # 初始化OOB预测数组
        oob_predictions = np.zeros((n_samples, len(np.unique(y))))
        oob_samples_count = np.zeros(n_samples)
        
        # 训练n_estimators棵树
        for _ in range(self.n_estimators):
            # 自助采样
            X_bootstrap, y_bootstrap, oob_indices = self._bootstrap_sample(X, y)
            
            # 创建决策树并设置随机特征选择
            tree = DecisionTreeClassifier(
                max_features=self.max_features_used,
                max_depth=self.max_depth
            )
            tree.fit(X_bootstrap, y_bootstrap)
            self.trees.append(tree)
            
            # 计算袋外样本预测
            if len(oob_indices) > 0:
                oob_pred = tree.predict_proba(X[oob_indices])
                oob_predictions[oob_indices] += oob_pred
                oob_samples_count[oob_indices] += 1
        
        # 计算OOB分数
        valid_oob = oob_samples_count > 0
        if np.any(valid_oob):
            oob_predictions_valid = oob_predictions[valid_oob]
            oob_samples_count_valid = oob_samples_count[valid_oob, np.newaxis]
            oob_predictions_avg = oob_predictions_valid / oob_samples_count_valid
            y_pred = np.argmax(oob_predictions_avg, axis=1)
            self.oob_score_ = np.mean(y[valid_oob] == y_pred)
        
        return self
    
    def predict(self, X):
        # 收集所有树的预测
        predictions = np.array([tree.predict(X) for tree in self.trees])
        # 投票得到最终预测
        return np.apply_along_axis(
            lambda x: np.bincount(x).argmax(),
            axis=0,
            arr=predictions)
    
    def predict_proba(self, X):
        # 收集所有树的概率预测并平均
        probas = np.array([tree.predict_proba(X) for tree in self.trees])
        return np.mean(probas, axis=0)
    
    def feature_importances_(self):
        # 计算平均特征重要性
        importances = np.mean([tree.feature_importances_ for tree in self.trees], axis=0)
        return importances

5.算法调优与最佳实践

5.1 主要超参数

（1） n_estimators：基学习器数量，通常越多越好，但会增加计算成本。

（2） max_features：每个节点随机选择的特征数：

分类建议： $\sqrt{d}$

回归建议： $d/3$

（3） max_depth：树的最大深度，控制复杂度。

（4） min_samples_split：分裂内部节点所需的最小样本数。

（5） min_samples_leaf：叶节点所需的最小样本数。

5.2超参数调优示例

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split, GridSearchCV, learning_curve
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix, roc_curve, auc
import time
import warnings
from matplotlib.font_manager import FontProperties
import platform
import os
import tempfile

# 为多进程操作创建一个纯ASCII字符的临时目录路径
temp_dir = tempfile.mkdtemp(prefix='sklearn_rf_')
os.environ['JOBLIB_TEMP_FOLDER'] = temp_dir
print(f"临时文件夹路径: {temp_dir}")

# 忽略警告
warnings.filterwarnings("ignore")

# 设置中文字体
def setup_chinese_font():
    system = platform.system()
    
    if system == 'Windows':
        font_paths = [
            'C:/Windows/Fonts/simhei.ttf',    # 黑体
            'C:/Windows/Fonts/simsun.ttc',    # 宋体
            'C:/Windows/Fonts/msyh.ttc',      # 微软雅黑
            'C:/Windows/Fonts/simfang.ttf',   # 仿宋
        ]
    elif system == 'Darwin':  # macOS
        font_paths = [
            '/System/Library/Fonts/PingFang.ttc',
            '/Library/Fonts/STHeiti Light.ttc',
            '/Library/Fonts/Songti.ttc',
        ]
    else:  # Linux
        font_paths = [
            '/usr/share/fonts/truetype/wqy/wqy-microhei.ttc',
            '/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc',
            '/usr/share/fonts/truetype/arphic/uming.ttc',
        ]
    
    for font_path in font_paths:
        if os.path.exists(font_path):
            print(f"使用字体: {font_path}")
            return FontProperties(fname=font_path)
    
    print("未找到指定的中文字体文件，将尝试使用系统配置的字体")
    return None

chinese_font = setup_chinese_font()

# 配置matplotlib全局字体设置
if chinese_font is not None:
    plt.rcParams['font.family'] = chinese_font.get_family()
    plt.rcParams['font.sans-serif'] = [chinese_font.get_name()] + plt.rcParams['font.sans-serif']
else:
    plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans', 'Arial']
plt.rcParams['axes.unicode_minus'] = False

# 设置美观的图表风格
plt.style.use('ggplot')

print("随机森林超参数调优实验")
print("-" * 50)

# 1. 生成数据
print("\n[步骤1] 生成分类数据集...")
X, y = make_classification(
    n_samples=1000,           # 样本数量
    n_features=20,            # 特征数量
    n_informative=10,         # 信息特征的数量
    n_redundant=5,            # 冗余特征的数量
    n_repeated=0,             # 重复特征的数量
    n_classes=2,              # 分类数量
    flip_y=0.1,               # 随机翻转标签的比例
    class_sep=1.0,            # 类别间的分离度
    random_state=42           # 随机种子
)

# 2. 数据预处理
print("[步骤2] 划分训练集和测试集...")
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print(f"训练集大小: {X_train.shape}")
print(f"测试集大小: {X_test.shape}")
print(f"特征数量: {X_train.shape[1]}")

# 3. 定义参数网格 - 为了加快运行速度，缩小参数空间
print("\n[步骤3] 定义参数网格...")
# 第一阶段：粗调参数 - 简化版本
param_grid_coarse = {
    'n_estimators': [50, 100],            # 树的数量
    'max_depth': [None, 10],              # 树的最大深度
    'min_samples_split': [2, 5],          # 内部节点再划分所需的最小样本数
    'min_samples_leaf': [1, 2],           # 叶节点所需的最小样本数
    'max_features': ['sqrt', 'log2']      # 寻找最佳分割时考虑的特征数
}

print("粗调参数网格:")
for param, values in param_grid_coarse.items():
    print(f"- {param}: {values}")

# 4. 创建基础模型
print("\n[步骤4] 创建基础随机森林模型...")
rf_base = RandomForestClassifier(random_state=42)

# 5. 创建并执行网格搜索 - 粗调阶段
print("\n[步骤5] 执行粗调参数的网格搜索(可能需要较长时间)...")
start_time = time.time()
grid_search_coarse = GridSearchCV(
    estimator=rf_base,
    param_grid=param_grid_coarse,
    scoring='accuracy',
    cv=3,                      # 3折交叉验证，加快速度
    n_jobs=-1,                 # 使用所有CPU核心
    verbose=1,                 # 显示进度
    return_train_score=True    # 返回训练集得分，用于分析过拟合
)

try:
    grid_search_coarse.fit(X_train, y_train)
    coarse_time = time.time() - start_time

    print(f"\n粗调参数完成，耗时: {coarse_time:.2f}秒")
    print(f"最佳参数组合: {grid_search_coarse.best_params_}")
    print(f"最佳交叉验证准确率: {grid_search_coarse.best_score_:.4f}")

    # 6. 基于粗调结果进行精调
    print("\n[步骤6] 基于粗调结果定义精调参数网格...")

    # 从粗调中获取最佳参数
    best_n_estimators = grid_search_coarse.best_params_['n_estimators']
    best_max_depth = grid_search_coarse.best_params_['max_depth']
    best_min_samples_split = grid_search_coarse.best_params_['min_samples_split']
    best_min_samples_leaf = grid_search_coarse.best_params_['min_samples_leaf']
    best_max_features = grid_search_coarse.best_params_['max_features']

    # 根据粗调结果定义更精细的参数网格 - 简化版本
    param_grid_fine = {
        'n_estimators': [best_n_estimators, best_n_estimators + 50],
        'max_features': [best_max_features],
    }

    # 对max_depth特别处理
    if best_max_depth is None:
        param_grid_fine['max_depth'] = [None, 15]
    else:
        param_grid_fine['max_depth'] = [best_max_depth, best_max_depth + 5]

    # 添加其他参数的精细搜索
    param_grid_fine['min_samples_split'] = [best_min_samples_split, best_min_samples_split + 1]
    param_grid_fine['min_samples_leaf'] = [best_min_samples_leaf, best_min_samples_leaf + 1]

    # 添加其他可能影响性能的参数
    param_grid_fine['bootstrap'] = [True]
    param_grid_fine['criterion'] = ['gini', 'entropy']

    print("精调参数网格:")
    for param, values in param_grid_fine.items():
        print(f"- {param}: {values}")

    # 7. 执行精调网格搜索
    print("\n[步骤7] 执行精调参数的网格搜索(可能需要较长时间)...")
    start_time = time.time()
    grid_search_fine = GridSearchCV(
        estimator=rf_base,
        param_grid=param_grid_fine,
        scoring='accuracy',
        cv=3,                  # 3折交叉验证，加快速度
        n_jobs=-1,
        verbose=1,
        return_train_score=True
    )

    grid_search_fine.fit(X_train, y_train)
    fine_time = time.time() - start_time

    print(f"\n精调参数完成，耗时: {fine_time:.2f}秒")
    print(f"最终最佳参数组合: {grid_search_fine.best_params_}")
    print(f"最终最佳交叉验证准确率: {grid_search_fine.best_score_:.4f}")

    # 8. 使用最佳参数评估模型
    print("\n[步骤8] 使用最佳参数评估模型性能...")
    best_rf = grid_search_fine.best_estimator_
    y_pred = best_rf.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)

    print(f"测试集准确率: {accuracy:.4f}")
    print("\n分类报告:")
    print(classification_report(y_test, y_pred))

    # 9. 可视化结果
    print("\n[步骤9] 可视化评估结果...")

    # 9.1 混淆矩阵
    plt.figure(figsize=(10, 8))
    cm = confusion_matrix(y_test, y_pred)
    sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
    plt.title('随机森林最佳模型混淆矩阵', fontsize=14)
    plt.xlabel('预测标签', fontsize=12)
    plt.ylabel('真实标签', fontsize=12)
    if chinese_font:
        plt.title('随机森林最佳模型混淆矩阵', fontproperties=chinese_font, fontsize=14)
        plt.xlabel('预测标签', fontproperties=chinese_font, fontsize=12)
        plt.ylabel('真实标签', fontproperties=chinese_font, fontsize=12)
    plt.tight_layout()
    plt.savefig('rf_confusion_matrix.png', dpi=300, bbox_inches='tight')
    plt.show()

    # 9.2 ROC曲线
    plt.figure(figsize=(10, 8))
    y_scores = best_rf.predict_proba(X_test)[:, 1]
    fpr, tpr, _ = roc_curve(y_test, y_scores)
    roc_auc = auc(fpr, tpr)

    plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.3f})')
    plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('假阳性率', fontsize=12)
    plt.ylabel('真阳性率', fontsize=12)
    plt.title('随机森林最佳模型ROC曲线', fontsize=14)
    plt.legend(loc="lower right")
    if chinese_font:
        plt.xlabel('假阳性率', fontproperties=chinese_font, fontsize=12)
        plt.ylabel('真阳性率', fontproperties=chinese_font, fontsize=12)
        plt.title('随机森林最佳模型ROC曲线', fontproperties=chinese_font, fontsize=14)
        for text in plt.legend().get_texts():
            text.set_fontproperties(chinese_font)
    plt.tight_layout()
    plt.savefig('rf_roc_curve.png', dpi=300, bbox_inches='tight')
    plt.show()

    # 9.3 特征重要性
    plt.figure(figsize=(12, 10))
    importances = best_rf.feature_importances_
    indices = np.argsort(importances)[::-1]

    plt.bar(range(X_train.shape[1]), importances[indices], align='center')
    plt.xticks(range(X_train.shape[1]), [f'特征 {i}' for i in indices], rotation=90)
    plt.title('随机森林特征重要性', fontsize=14)
    plt.xlabel('特征', fontsize=12)
    plt.ylabel('重要性', fontsize=12)
    if chinese_font:
        plt.title('随机森林特征重要性', fontproperties=chinese_font, fontsize=14)
        plt.xlabel('特征', fontproperties=chinese_font, fontsize=12)
        plt.ylabel('重要性', fontproperties=chinese_font, fontsize=12)
        plt.xticks(rotation=90, fontproperties=chinese_font)
    plt.tight_layout()
    plt.savefig('rf_feature_importance.png', dpi=300, bbox_inches='tight')
    plt.show()

    # 9.4 参数重要性
    def plot_param_importance(grid_search, title):
        plt.figure(figsize=(14, 10))
        
        results = pd.DataFrame(grid_search.cv_results_)
        
        # 提取参数名称
        param_names = [p for p in results.columns if p.startswith('param_')]
        
        # 创建一个包含每个参数的单独子图
        n_params = len(param_names)
        n_cols = 2
        n_rows = (n_params + 1) // 2
        
        for i, param_name in enumerate(param_names):
            plt.subplot(n_rows, n_cols, i + 1)
            
            # 提取参数的实际名称(不含"param_"前缀)
            param = param_name[6:]
            
            # 获取参数值和对应的平均测试分数
            param_values = results[param_name].astype(str)
            unique_values = param_values.unique()
            
            # 对于每个唯一的参数值，计算其平均测试分数
            mean_scores = [results[param_values == val]['mean_test_score'].mean() for val in unique_values]
            
            # 创建条形图
            plt.bar(range(len(unique_values)), mean_scores)
            plt.xticks(range(len(unique_values)), unique_values, rotation=45)
            plt.title(f'参数 {param} 的影响', fontsize=12)
            plt.xlabel(param, fontsize=10)
            plt.ylabel('平均测试分数', fontsize=10)
            if chinese_font:
                plt.title(f'参数 {param} 的影响', fontproperties=chinese_font, fontsize=12)
                plt.xlabel(param, fontproperties=chinese_font, fontsize=10)
                plt.ylabel('平均测试分数', fontproperties=chinese_font, fontsize=10)
        
        plt.suptitle(title, fontsize=16)
        if chinese_font:
            plt.suptitle(title, fontproperties=chinese_font, fontsize=16)
        plt.tight_layout(rect=[0, 0, 1, 0.96])
        plt.savefig('rf_param_importance.png', dpi=300, bbox_inches='tight')
        plt.show()

    # 显示精调参数的重要性
    plot_param_importance(grid_search_fine, '随机森林参数重要性分析')

    # 9.5 学习曲线
    train_sizes, train_scores, test_scores = learning_curve(
        best_rf, X_train, y_train, cv=3, n_jobs=-1,
        train_sizes=np.linspace(0.1, 1.0, 5)  # 减少点数以加快速度
    )

    train_mean = np.mean(train_scores, axis=1)
    train_std = np.std(train_scores, axis=1)
    test_mean = np.mean(test_scores, axis=1)
    test_std = np.std(test_scores, axis=1)

    plt.figure(figsize=(10, 8))
    plt.plot(train_sizes, train_mean, color='blue', marker='o', markersize=5, label='训练集分数')
    plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std, alpha=0.15, color='blue')
    plt.plot(train_sizes, test_mean, color='green', marker='s', markersize=5, label='验证集分数')
    plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15, color='green')
    plt.title('随机森林最佳模型学习曲线', fontsize=14)
    plt.xlabel('训练样本数', fontsize=12)
    plt.ylabel('准确率', fontsize=12)
    plt.grid(True)
    plt.legend(loc='lower right')
    if chinese_font:
        plt.title('随机森林最佳模型学习曲线', fontproperties=chinese_font, fontsize=14)
        plt.xlabel('训练样本数', fontproperties=chinese_font, fontsize=12)
        plt.ylabel('准确率', fontproperties=chinese_font, fontsize=12)
        for text in plt.legend().get_texts():
            text.set_fontproperties(chinese_font)
    plt.tight_layout()
    plt.savefig('rf_learning_curve.png', dpi=300, bbox_inches='tight')
    plt.show()

    # 10. 总结最佳模型配置
    print("\n[步骤10] 最终随机森林模型配置:")
    for param, value in best_rf.get_params().items():
        print(f"- {param}: {value}")

    print("\n超参数调优实验完成！")
    print(f"总耗时: {coarse_time + fine_time:.2f}秒")
    print(f"最终模型测试集准确率: {accuracy:.4f}")

except Exception as e:
    print(f"发生错误: {str(e)}")
    print("尝试不使用并行处理的简化版本...")
    
    # 如果并行处理失败，尝试使用简化版本（不使用并行）
    rf_base = RandomForestClassifier(
        n_estimators=100,
        max_depth=10,
        min_samples_split=2,
        min_samples_leaf=1,
        max_features='sqrt',
        random_state=42
    )
    
    rf_base.fit(X_train, y_train)
    y_pred = rf_base.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    
    print(f"\n使用默认参数的随机森林模型准确率: {accuracy:.4f}")
    print("\n分类报告:")
    print(classification_report(y_test, y_pred))
    
    # 简单的可视化
    plt.figure(figsize=(12, 10))
    importances = rf_base.feature_importances_
    indices = np.argsort(importances)[::-1]

    plt.bar(range(X_train.shape[1]), importances[indices], align='center')
    plt.xticks(range(X_train.shape[1]), [f'特征 {i}' for i in indices], rotation=90)
    plt.title('随机森林特征重要性 (默认参数)', fontsize=14)
    plt.xlabel('特征', fontsize=12)
    plt.ylabel('重要性', fontsize=12)
    if chinese_font:
        plt.title('随机森林特征重要性 (默认参数)', fontproperties=chinese_font, fontsize=14)
        plt.xlabel('特征', fontproperties=chinese_font, fontsize=12)
        plt.ylabel('重要性', fontproperties=chinese_font, fontsize=12)
        plt.xticks(rotation=90, fontproperties=chinese_font)
    plt.tight_layout()
    plt.savefig('rf_feature_importance_default.png', dpi=300, bbox_inches='tight')
    plt.show()

finally:
    # 清理临时文件夹
    import shutil
    try:
        shutil.rmtree(temp_dir)
        print(f"已清理临时文件夹: {temp_dir}")
    except:
        pass

程序运行结果如下：

临时文件夹路径: C:\Users\ABC\AppData\Local\Temp\sklearn_rf_iyndeds8
使用字体: C:/Windows/Fonts/simhei.ttf
随机森林超参数调优实验
--------------------------------------------------

[步骤1] 生成分类数据集...
[步骤2] 划分训练集和测试集...
训练集大小: (800, 20)
测试集大小: (200, 20)
特征数量: 20

[步骤3] 定义参数网格...
粗调参数网格:
- n_estimators: [50, 100]
- max_depth: [None, 10]
- min_samples_split: [2, 5]
- min_samples_leaf: [1, 2]
- max_features: ['sqrt', 'log2']

[步骤4] 创建基础随机森林模型...

[步骤5] 执行粗调参数的网格搜索(可能需要较长时间)...
发生错误: 'ascii' codec can't encode characters in position 18-20: ordinal not in range(128)
尝试不使用并行处理的简化版本...

使用默认参数的随机森林模型准确率: 0.8850

分类报告:
precision recall f1-score support

0 0.91 0.84 0.87 93
1 0.87 0.93 0.90 107

accuracy 0.89 200
macro avg 0.89 0.88 0.88 200
weighted avg 0.89 0.89 0.88 200

已清理临时文件夹: C:\Users\ABC\AppData\Local\Temp\sklearn_rf_iyndeds8

三、集成学习器

1. 集成学习的基本原理

1.1 集成学习的定义

集成学习通过构建并结合多个学习器来完成学习任务，其目标是通过集成的方式获得比单一学习器更好的泛化性能。形式化地，给定训练数据集 $D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$ ，集成学习首先生成 $T$ 个基学习器 $\{h_1, h_2, \ldots, h_T\}$ ，然后将它们进行结合，得到最终的集成学习器 $H$ 。

1.2 集成学习的理论基础

集成学习的理论基础主要基于两个方面：偏差-方差分解和"无免费午餐"定理。

1.2.1 偏差-方差分解

对于回归问题，学习器 $h$ 的预测误差可分解为：

$E[(h(x) - y)^2] = (E[h(x)] - y)^2 + E[(h(x) - E[h(x)])^2]$

即：误差 = 偏差^2 + 方差

偏差：表示预测值的期望与真实值之间的差异，反映了模型的拟合能力。

方差：表示预测值的波动程度，反映了模型的稳定性。

集成学习通常能够在不增加偏差的情况下减少方差，从而提高模型性能。

1.2.2 集成学习的分类

根据集成的方式，集成学习主要分为三类：

（1） Bagging (Bootstrap Aggregating)：通过有放回采样生成多个训练集，在每个训练集上独立训练一个基学习器，最后通过投票或平均组合。

（2） Boosting：串行训练基学习器，每个新的基学习器都关注前一个基学习器错误预测的样本。

（3） Stacking：训练一个元学习器来组合多个基学习器的预测结果。

2. Bagging与随机森林

2.1 Bagging算法

Bagging是Bootstrap Aggregating的缩写，其基本思想是使用自助采样法（bootstrap sampling）从原始数据集中有放回地采样，生成多个训练子集，然后在每个子集上训练一个基学习器，最后通过投票或平均的方式结合这些基学习器。

数学表示

给定训练集 $D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$ ：

（1）对于 $t = 1, 2, \ldots, T$ ：

a.通过自助采样（有放回抽样）从 $D$ 中选择 $n$ 个样本，形成训练子集 $D_t$ 。

b.在 $D_t$ 上训练出基学习器 $h_t$ 。

（2）对于分类问题，最终预测为：

$H(x) = \arg\max_y \sum_{t=1}^T \mathbf{1}(h_t(x) = y)$

对于回归问题，最终预测为：

$H(x) = \frac{1}{T}\sum_{t=1}^T h_t(x)$

2.2 随机森林算法

随机森林是Bagging的一个特例，它使用决策树作为基学习器，并在训练过程中引入额外的随机性。

随机森林的两层随机性：

（1）样本随机性：与Bagging相同，使用自助采样生成训练子集。

（2）.特征随机性：在决策树的每个节点，只考虑特征的随机子集而非全部特征。

数学表示

（1）对于 $t = 1, 2, \ldots, T$ ：

a.通过自助采样从训练集 $D$ 中选择 $n$ 个样本，形成 $D_t$ 。

b.训练决策树 $h_t$ ，在每个节点：

（a）随机选择 $m$ 个特征（通常 $m = \sqrt{d}$ ，其中 $d$ 是特征总数）。

（b）在这 $m$ 个特征中找到最佳分割。

（2）集成预测同Bagging。

2.3 袋外估计(Out-of-Bag Estimation)

在Bagging和随机森林中，每个训练子集 $D_t$ 约包含原始训练集中63.2%的样本，剩余的约36.8%样本称为"袋外样本"，可用于评估模型性能。

袋外误差计算公式：

$\epsilon_{oob} = \frac{1}{n}\sum_{i=1}^n \mathbf{1}\left(y_i \neq \arg\max_y \sum_{t:x_i \notin D_t} \mathbf{1}(h_t(x_i) = y)\right)$

其中 $x_i \notin D_t$ 表示 $x_i$ 是第 $t$ 个基学习器的袋外样本。

3. Boosting算法

3.1 AdaBoost算法

AdaBoost（Adaptive Boosting）是最早的Boosting算法之一，其核心思想是按照迭代的方式，每一轮根据上一轮的结果调整样本权重，使得之前被错误分类的样本在新一轮中获得更高的权重。

算法步骤

（1）初始化样本权重： $D_1(i) = 1/n$ ，对所有 $i = 1, 2, \ldots, n$ 。

（2）对于 $t = 1, 2, \ldots, T$ ：

a.使用具有权重 $D_t$ 的训练集训练基学习器 $h_t$ 。

b.计算 $h_t$ 的加权错误率：

$\epsilon_t = \sum_{i=1}^n D_t(i) \cdot \mathbf{1}(h_t(x_i) \neq y_i)$

c.计算 $h_t$ 的权重：

$\alpha_t = \frac{1}{2} \ln\left(\frac{1-\epsilon_t}{\epsilon_t}\right)$

d.更新样本权重：

$D_{t+1}(i) = \frac{D_t(i)}{Z_t} \exp(-\alpha_t y_i h_t(x_i))$

其中 $Z_t$ 是归一化因子。

（3）最终集成学习器：

$H(x) = \text{sign}\left(\sum_{t=1}^T \alpha_t h_t(x)\right)$

3.2 梯度提升(Gradient Boosting)

梯度提升是一种通用的提升框架，它将提升过程看作是在函数空间中优化一个损失函数的过程。

算法步骤

（1）初始化模型：

$F_0(x) = \arg\min_\gamma \sum_{i=1}^n L(y_i, \gamma)$

2. 对于 $t = 1, 2, \ldots, T$ ：

a. 计算负梯度：

$r_{it} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F=F_{t-1}}$

对所有 $i = 1, 2, \ldots, n$ 。

b.拟合基学习器 $h_t$ 到残差 $r_{it}$ 。

c. 找到最优步长：

$\gamma_t = \arg\min_\gamma \sum_{i=1}^n L(y_i, F_{t-1}(x_i) + \gamma h_t(x_i))$

d. 更新模型：

$F_t(x) = F_{t-1}(x) + \gamma_t h_t(x)$

(3) 最终模型： $F_T(x)$

特别地，对于平方损失 $L(y, F(x)) = \frac{1}{2}(y - F(x))^2$ ，负梯度恰好是残差： $r_{it} = y_i - F_{t-1}(x_i)$ 。

3.3 XGBoost算法

XGBoost（Extreme Gradient Boosting）是梯度提升的高效实现，增加了正则化项和使用二阶导数信息。

目标函数

XGBoost优化的目标函数为：

$\mathcal{L}(\phi) = \sum_{i=1}^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)$

其中 $l$ 是损失函数， $\Omega$ 是正则化项， $\hat{y}_i = \sum_{k=1}^K f_k(x_i)$ 是预测值， $f_k$ 是第 $k$ 个基学习器。

正则化项通常定义为：

$\Omega(f) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2$

其中 $T$ 是叶节点数量， $w_j$ 是第 $j$ 个叶节点的权重。

算法步骤

在迭代过程中，XGBoost通过泰勒展开来近似目标函数：

$\mathcal{L}^{(t)} \approx \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)$

其中 $g_i$ 和 $h_i$ 分别是损失函数关于当前预测值的一阶和二阶导数：

$g_i = \frac{\partial l(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)}}$

$h_i = \frac{\partial^2 l(y_i, \hat{y}_i^{(t-1)})}{\partial (\hat{y}_i^{(t-1)})^2}$

最优的树结构通过贪婪算法寻找，评估分裂点的指标为：

$Gain = \frac{1}{2} \left[ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} \right] - \gamma$

其中 $G_L$ 、 $G_R$ 、 $H_L$ 、 $H_R$ 分别是左右子节点的一阶导数和二阶导数之和。

4. Stacking算法

4.1 基本原理

Stacking（堆叠集成）是一种将多个基学习器的预测结果作为输入，训练元学习器（meta-learner）来组合这些预测的方法。

算法步骤

（1）训练第一层基学习器： $h_1, h_2, \ldots, h_K$ 。

（2）使用K折交叉验证生成每个基学习器在验证集上的预测。

（3）使用这些预测作为新特征，训练元学习器。

（4）在预测阶段：

a. 使用所有基学习器对新样本进行预测。

b. 将这些预测输入到元学习器中获得最终预测。

数学表示：

元学习器的训练数据： $\{([h_1(x_i), h_2(x_i), \ldots, h_K(x_i)], y_i) | i = 1, 2, \ldots, n\}$

预测函数： $H(x) = h_{meta}([h_1(x), h_2(x), \ldots, h_K(x)])$

4.2 变体和改进

（1）Blending：使用固定的验证集而非交叉验证。

（2）Super Learner：使用交叉验证生成元特征，并使用约束优化来确定元学习器的权重。

（3）Feature-weighted Linear Stacking：考虑原始特征对元学习器的贡献。

5. 集成学习的数学理论和优化

5.1 偏差-方差-协方差分解

对于回归问题，集成学习器的预测误差可以分解为：

$E[(H(x) - y)^2] = (E[H(x)] - y)^2 + E[(H(x) - E[H(x)])^2]$

对于平均集成，如果有$T$个基学习器，且它们的误差是独立同分布的，那么集成的方差为：

$Var(H(x)) = \frac{1}{T}Var(h(x))$

然而，在实际中，基学习器之间通常存在相关性，此时集成的方差为：

$Var(H(x)) = \rho \cdot Var(h(x)) + \frac{1-\rho}{T}Var(h(x))$

其中 $\rho$ 是基学习器之间的平均相关系数。这就解释了为什么我们需要基学习器之间既有准确性又有多样性。

5.2 多样性生成方法

（1）数据层面的多样性：

a. 样本扰动（如Bagging中的自助采样）.

b. 属性扰动（如随机森林中的特征子集选择）。

c. 输出表示扰动（如错误纠正输出编码）。

（2）学习器层面的多样性：

a. 不同的学习算法。

b. 同一算法的不同参数设置。

c. 初始化条件的变化（如神经网络的随机初始化）。

6. 实际应用中的集成学习

6.1 参数调优技巧

（1）基学习器数量：增加基学习器数量通常能提升性能，但会增加计算成本。

（2）采样策略：对于样本不平衡问题，可以使用分层采样或加权采样。

（3）学习率（针对提升方法）：较小的学习率通常能得到更好的泛化性能，但需要更多迭代。

（4）正则化：适当的正则化可以防止过拟合。

（5）早停：使用验证集确定最佳迭代次数。

6.2 集成学习的高级技巧

（1）异质集成：结合不同类型的基学习器。

（2）级联集成：多层集成结构。

（3）动态选择：根据测试样本动态选择子集成。

（4）多标签集成：处理多标签分类问题。

（5）深度集成：结合深度学习和集成学习。

7. 集成学习算法的Python实现示例

7.1 自定义AdaBoost实现

class AdaBoost:
    def __init__(self, n_estimators=50, learning_rate=1.0):
        self.n_estimators = n_estimators
        self.learning_rate = learning_rate
        self.estimators = []
        self.estimator_weights = []
        
    def fit(self, X, y):
        n_samples = len(X)
        # 初始化样本权重
        sample_weights = np.ones(n_samples) / n_samples
        
        for i in range(self.n_estimators):
            # 训练基学习器
            estimator = DecisionTreeClassifier(max_depth=1)  # 决策树桩
            estimator.fit(X, y, sample_weight=sample_weights)
            
            # 预测结果
            predictions = estimator.predict(X)
            
            # 计算加权错误率
            incorrect = (predictions != y)
            error = np.sum(sample_weights * incorrect) / np.sum(sample_weights)
            
            # 若错误率为0或大于等于0.5，则停止训练
            if error <= 0 or error >= 0.5:
                break
                
            # 计算基学习器权重
            alpha = self.learning_rate * 0.5 * np.log((1 - error) / error)
            
            # 更新样本权重
            sample_weights *= np.exp(-alpha * y * predictions)
            # 归一化权重
            sample_weights /= np.sum(sample_weights)
            
            # 保存基学习器和其权重
            self.estimators.append(estimator)
            self.estimator_weights.append(alpha)
            
        return self
        
    def predict(self, X):
        # 加权投票
        predictions = np.zeros(len(X))
        for alpha, estimator in zip(self.estimator_weights, self.estimators):
            predictions += alpha * estimator.predict(X)
            
        return np.sign(predictions)

7.2 自定义Stacking实现

class StackingClassifier:
    def __init__(self, base_classifiers, meta_classifier, n_folds=5):
        self.base_classifiers = base_classifiers
        self.meta_classifier = meta_classifier
        self.n_folds = n_folds
        
    def fit(self, X, y):
        # 训练基分类器
        for clf in self.base_classifiers:
            clf.fit(X, y)
            
        # 使用交叉验证生成元特征
        meta_features = np.zeros((X.shape[0], len(self.base_classifiers)))
        kf = KFold(n_splits=self.n_folds, shuffle=True, random_state=42)
        
        for i, clf in enumerate(self.base_classifiers):
            for train_idx, valid_idx in kf.split(X):
                # 在训练集上训练
                clone_clf = clone(clf)
                clone_clf.fit(X[train_idx], y[train_idx])
                # 在验证集上预测
                meta_features[valid_idx, i] = clone_clf.predict(X[valid_idx])
                
        # 训练元分类器
        self.meta_classifier.fit(meta_features, y)
        
        return self
        
    def predict(self, X):
        # 基分类器预测
        meta_features = np.column_stack([
            clf.predict(X) for clf in self.base_classifiers
        ])
        
        # 元分类器最终预测
        return self.meta_classifier.predict(meta_features)

四、提升算法

1. AdaBoost算法

1.1 基本原理

AdaBoost (Adaptive Boosting) 是最早的提升算法之一，由Freund和Schapire于1995年提出。其核心思想是：通过调整样本权重，使后续基学习器更加关注先前被错误分类的样本。

1.2 数学公式化描述

给定训练集 $D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$ ，其中 $y_i \in \{-1, +1\}$ 对于二分类问题。

算法步骤：

（1）初始化样本权重：

$D_1(i) = \frac{1}{n}, \quad i = 1, 2, \ldots, n$

（2）对于 $t = 1, 2, \ldots, T$ ：

a. 使用带权重分布 $D_t$ 的训练集训练基学习器 $h_t$ 。

b. 计算 $h_t$ 的加权错误率：

$\epsilon_t = \sum_{i=1}^n D_t(i) \cdot \mathbf{1}(h_t(x_i) \neq y_i)$

c. 计算 $h_t$ 的权重：

$\alpha_t = \frac{1}{2} \ln \left( \frac{1 - \epsilon_t}{\epsilon_t} \right)$

d. 更新样本权重分布：

$D_{t+1}(i) = \frac{D_t(i)}{Z_t} \exp(-\alpha_t \cdot y_i \cdot h_t(x_i))$

其中 $Z_t$ 是归一化因子，确保 $D_{t+1}$ 是一个分布：

$Z_t = \sum_{i=1}^n D_t(i) \exp(-\alpha_t \cdot y_i \cdot h_t(x_i))$

（3）构建最终的强分类器：

$H(x) = \text{sign}\left( \sum_{t=1}^T \alpha_t h_t(x) \right)$

1.3 理论保证

AdaBoost在训练集上的错误率(trainerrorrate)上界可以证明为：

$\text{trainerrorrate} \leq \exp\left(-2\sum_{t=1}^T \left(\frac{1}{2} - \epsilon_t\right)^2\right)$

只要每个基学习器的错误率 $\epsilon_t < 0.5$ （比随机猜测好），随着基学习器数量 $T$ 的增加，训练错误率将指数级下降。

1.4 AdaBoost变种

（1）AdaBoost.M1：二分类版本，如上所述。

（2）AdaBoost.M2：用于多分类问题，引入伪损失概念：

$\text{pseudoloss}_t = \frac{1}{2} \sum_{i=1}^n \sum_{y \neq y_i} D_t(i, y) (1 - h_t(x_i, y_i) + h_t(x_i, y))$

（3）AdaBoost.R：用于回归问题，将回归问题转换为分类问题处理。

2. 梯度提升(Gradient Boosting)

2.1 基本原理

梯度提升(Gradient Boosting)由Friedman于2001年提出，是一个更加一般化的提升框架，它将提升过程视为一个数值优化问题，利用梯度下降来最小化损失函数。

2.2 数学公式化描述

给定损失函数 $L(y, F(x))$ 和训练集 $D = \{(x_i, y_i)\}_{i=1}^n$ 。

算法步骤：

（1）初始化模型：

$F_0(x) = \arg\min_{\gamma} \sum_{i=1}^n L(y_i, \gamma)$

通常对于回归问题， $F_0(x) = \bar{y}$ （样本均值）；对于分类问题，可以是对数几率函数的初始值。

（2）对于 $m = 1, 2, \ldots, M$ ：

a. 计算当前模型的负梯度（也称为残差或伪残差）：

$r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F=F_{m-1}} \quad \text{for } i = 1, 2, \ldots, n$

对于平方损失 $L(y, F) = \frac{1}{2}(y - F)^2$ ，负梯度就是普通残差 $r_{im} = y_i - F_{m-1}(x_i)$ 。

b. 拟合一个基学习器 $h_m(x)$ 到残差 $\{(x_i, r_{im})\}_{i=1}^n$ 上

c. 计算最优步长（学习率）：

$\rho_m = \arg\min_{\rho} \sum_{i=1}^n L(y_i, F_{m-1}(x_i) + \rho h_m(x_i))$

d. 更新模型：

$F_m(x) = F_{m-1}(x) + \eta \rho_m h_m(x)$

其中 $\eta$ 是收缩参数（学习率），通常取较小的值如0.1。

（3）最终模型：

$F_M(x) = F_0(x) + \sum_{m=1}^M \eta \rho_m h_m(x)$

2.3 常用损失函数

（1）平方损失（回归）： $L(y, F) = \frac{1}{2}(y - F)^2$

（2）绝对损失（回归）： $L(y, F) = |y - F|$

（3）对数损失（分类）： $L(y, F) = \log(1 + e^{-yF})$ ，其中 $y \in \{-1, 1\}$

（4）指数损失（分类）： $L(y, F) = e^{-yF}$

（5） Huber损失（鲁棒回归）：结合平方损失和绝对损失的优点

2.4 GBDT (Gradient Boosting Decision Tree)

GBDT是使用决策树作为基学习器的梯度提升方法。GBDT的每一棵树都试图拟合前面模型的残差，最终形成一个加法模型。

3. XGBoost (Extreme Gradient Boosting)

3.1 基本原理

XGBoost是由陈天奇等人开发的GBDT优化版本，通过引入正则化项和更高效的算法实现，大大提高了性能和效率。

3.2 数学公式化描述

目标函数：

$\mathcal{L}(\Phi) = \sum_{i=1}^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)$

其中：

$\hat{y}_i = \sum_{k=1}^K f_k(x_i)$ 是预测值

$f_k$ 表示第 $k$ 个树模型

$\Omega(f_k)$ 是正则化项，定义为：

$\Omega(f) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2$

其中 $T$ 是叶节点数量， $w_j$ 是第 $j$ 个叶节点的权重， $\gamma$ 和 $\lambda$ 是控制正则化强度的参数。

迭代过程：

XGBoost采用加法训练，在第 $t$ 轮添加一棵树 $f_t$ ：

$\hat{y}_i^{(t)} = \hat{y}_i^{(t-1)} + f_t(x_i)$

目标函数可以使用二阶泰勒展开近似为：

$\mathcal{L}^{(t)} \approx \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)] + \Omega(f_t)$

其中：

$g_i = \frac{\partial l(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)}}$ 是损失函数对当前预测值的一阶导数

$h_i = \frac{\partial^2 l(y_i, \hat{y}_i^{(t-1)})}{(\partial \hat{y}_i^{(t-1)})^2}$ 是二阶导数

树的构建：

对于具有 $T$ 个叶节点的树 $f_t$ ，定义叶节点 $j$ 的样本集为 $I_j = \{i | q(x_i) = j\}$ ，其中 $q(x)$ 将样本映射到叶节点。

目标函数可以重写为：

$\mathcal{L}^{(t)} \approx \sum_{j=1}^T \left[(\sum_{i \in I_j} g_i) w_j + \frac{1}{2}(\sum_{i \in I_j} h_i + \lambda) w_j^2 \right] + \gamma T$

最优叶节点权重为：

$w_j^* = -\frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j} h_i + \lambda}$

最优目标函数值为：

$\mathcal{L}^{(t)}(q) = -\frac{1}{2}\sum_{j=1}^T \frac{(\sum_{i \in I_j} g_i)^2}{\sum_{i \in I_j} h_i + \lambda} + \gamma T$

分裂增益：

对于候选分裂，增益计算为：

$Gain = \frac{1}{2}\left[\frac{(\sum_{i \in I_L} g_i)^2}{\sum_{i \in I_L} h_i + \lambda} + \frac{(\sum_{i \in I_R} g_i)^2}{\sum_{i \in I_R} h_i + \lambda} - \frac{(\sum_{i \in I} g_i)^2}{\sum_{i \in I} h_i + \lambda}\right] - \gamma$

其中 $I_L$ 和 $I_R$ 分别是分裂后的左右子节点样本集合。

3.3 XGBoost的关键创新

（1）正则化：通过正则项控制模型复杂度。

（2）二阶近似：使用二阶导数加速优化过程。

（3）列抽样：类似随机森林的特征子采样，减少过拟合。

（4）稀疏感知算法：高效处理稀疏数据。

（5）基于权重的分位数草图：高效处理连续特征。

（6）缓存感知访问：优化数据访问模式。

（7） out-of-core计算：能够处理无法装入内存的大数据集。

4.Python代码实现

4.1AdaBoost实现示例

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 生成数据
X, y = make_classification(n_samples=1000, n_features=10,
                          n_informative=5, n_redundant=3,
                          random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练AdaBoost模型
base_estimator = DecisionTreeClassifier(max_depth=1)  # 决策树桩
adaboost = AdaBoostClassifier(n_estimators=50,
                             learning_rate=1.0,
                             random_state=42)
adaboost.fit(X_train, y_train)

# 预测
y_pred = adaboost.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"AdaBoost准确率: {accuracy:.4f}")

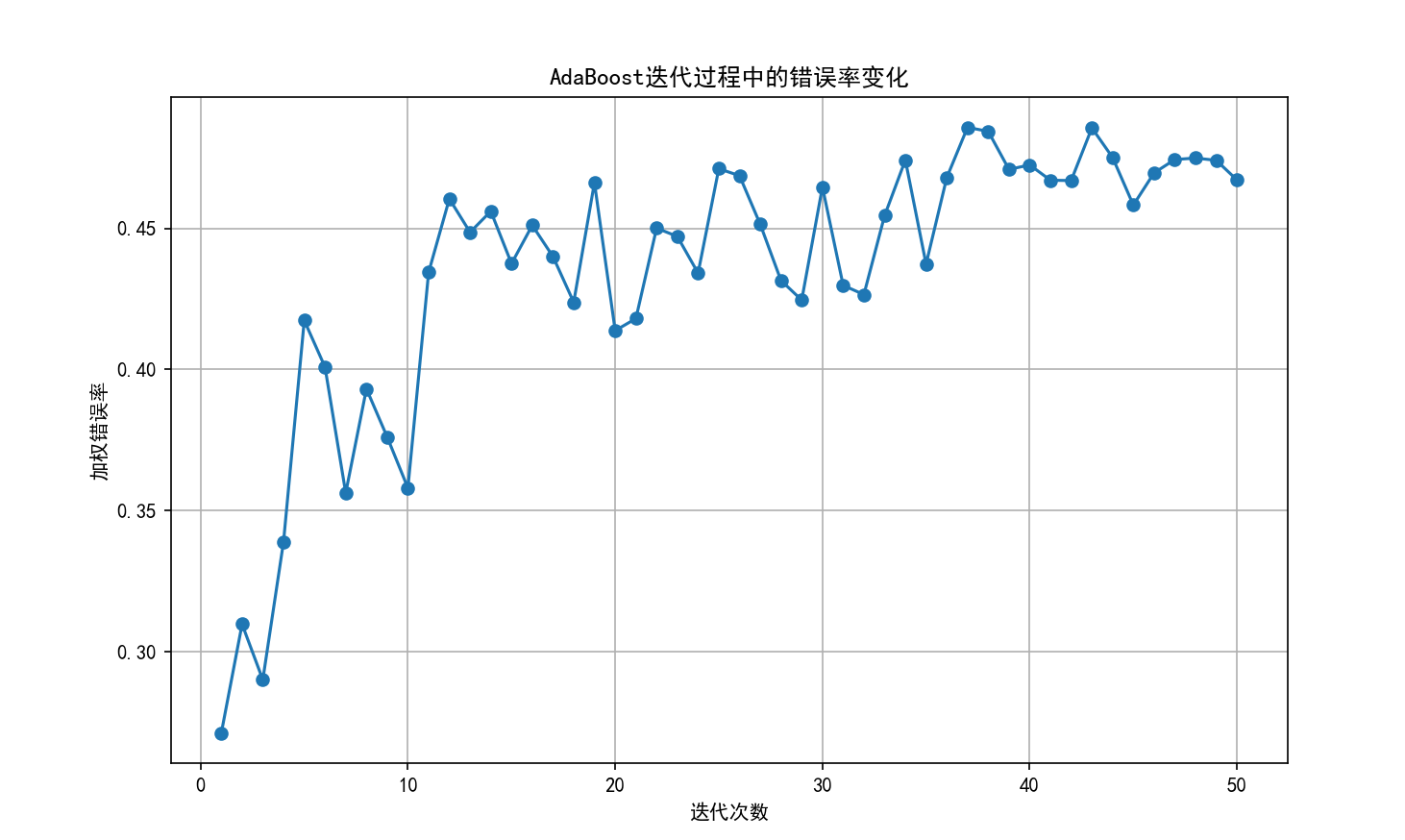
# 绘制错误率随迭代次数的变化
estimator_errors = adaboost.estimator_errors_
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(estimator_errors) + 1), estimator_errors, marker='o')
plt.xlabel('迭代次数')
plt.ylabel('加权错误率')
plt.title('AdaBoost迭代过程中的错误率变化')
plt.grid(True)
plt.show()

程序运行结果如下

4.2梯度提升实现示例

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score, log_loss
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 生成数据
X, y = make_classification(n_samples=1000, n_features=10,
                          n_informative=5, n_redundant=3,
                          random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练GBDT模型
gbdt = GradientBoostingClassifier(n_estimators=100,
                                learning_rate=0.1,
                                max_depth=3,
                                subsample=0.8,
                                random_state=42)
gbdt.fit(X_train, y_train)

# 预测
y_pred = gbdt.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"GBDT准确率: {accuracy:.4f}")

# 绘制损失函数值随迭代次数的变化
test_deviance = np.zeros((gbdt.n_estimators,), dtype=np.float64)

# 正确的方法：使用staged_predict_proba而不是gbdt.loss
for i, y_proba in enumerate(gbdt.staged_predict_proba(X_test)):
    # 使用log_loss函数计算对数损失
    test_deviance[i] = log_loss(y_test, y_proba)

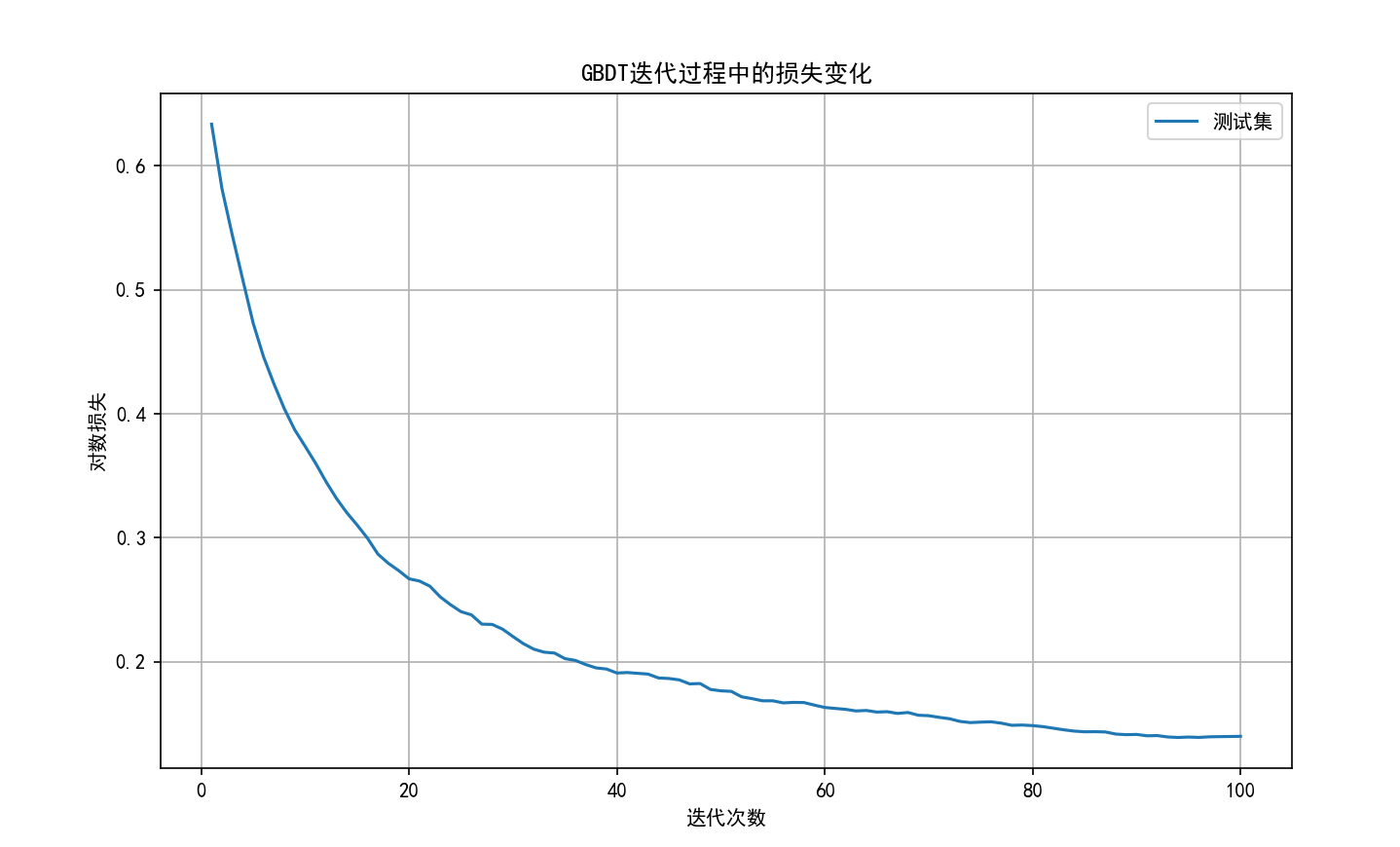
plt.figure(figsize=(10, 6))
plt.plot(np.arange(gbdt.n_estimators) + 1, test_deviance, label='测试集')
plt.xlabel('迭代次数')
plt.ylabel('对数损失')
plt.title('GBDT迭代过程中的损失变化')
plt.legend()
plt.grid(True)
plt.show()

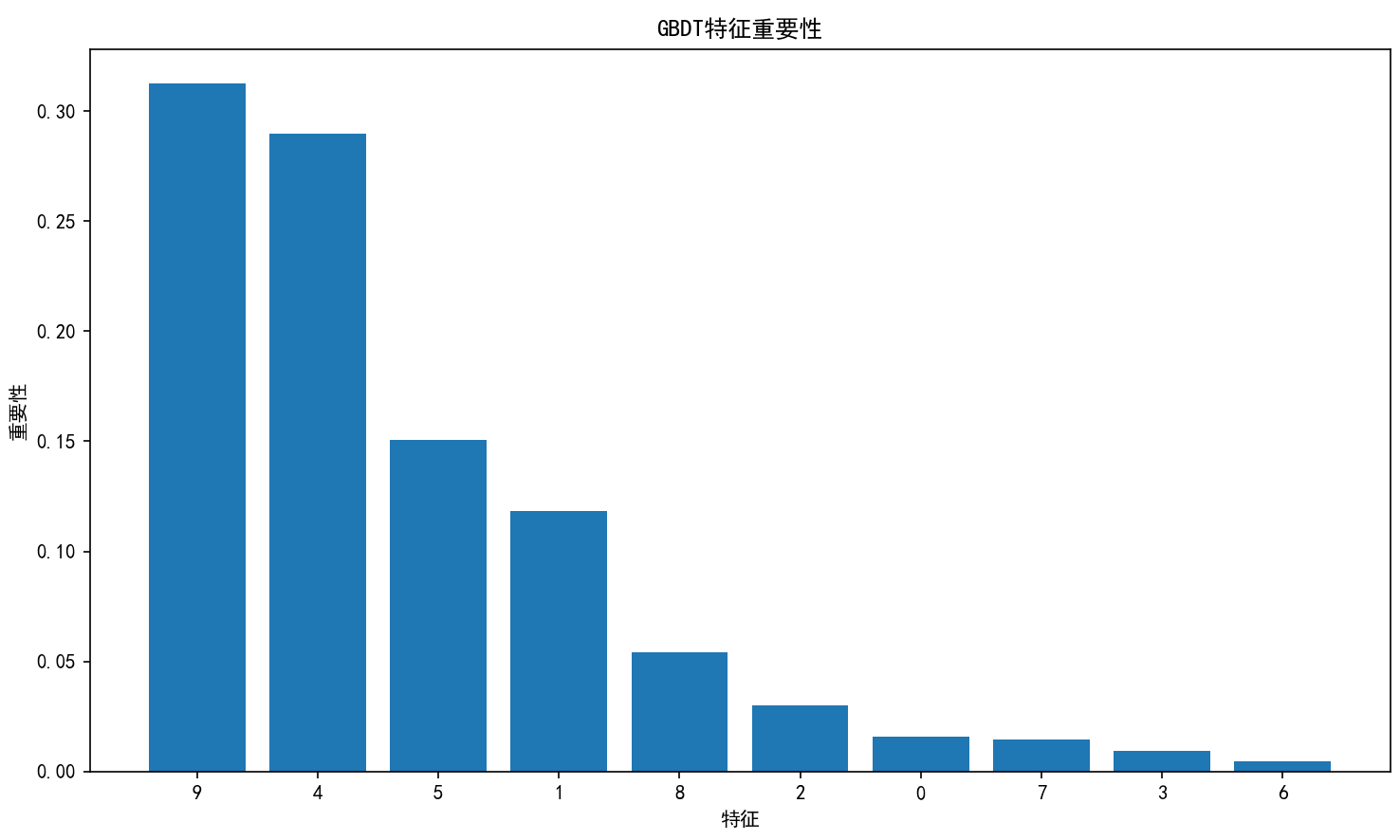
# 特征重要性
feature_importance = gbdt.feature_importances_
sorted_idx = np.argsort(feature_importance)[::-1]
plt.figure(figsize=(10, 6))
plt.bar(range(X_train.shape[1]), feature_importance[sorted_idx])
plt.xticks(range(X_train.shape[1]), sorted_idx)
plt.xlabel('特征')
plt.ylabel('重要性')
plt.title('GBDT特征重要性')
plt.tight_layout()
plt.show()

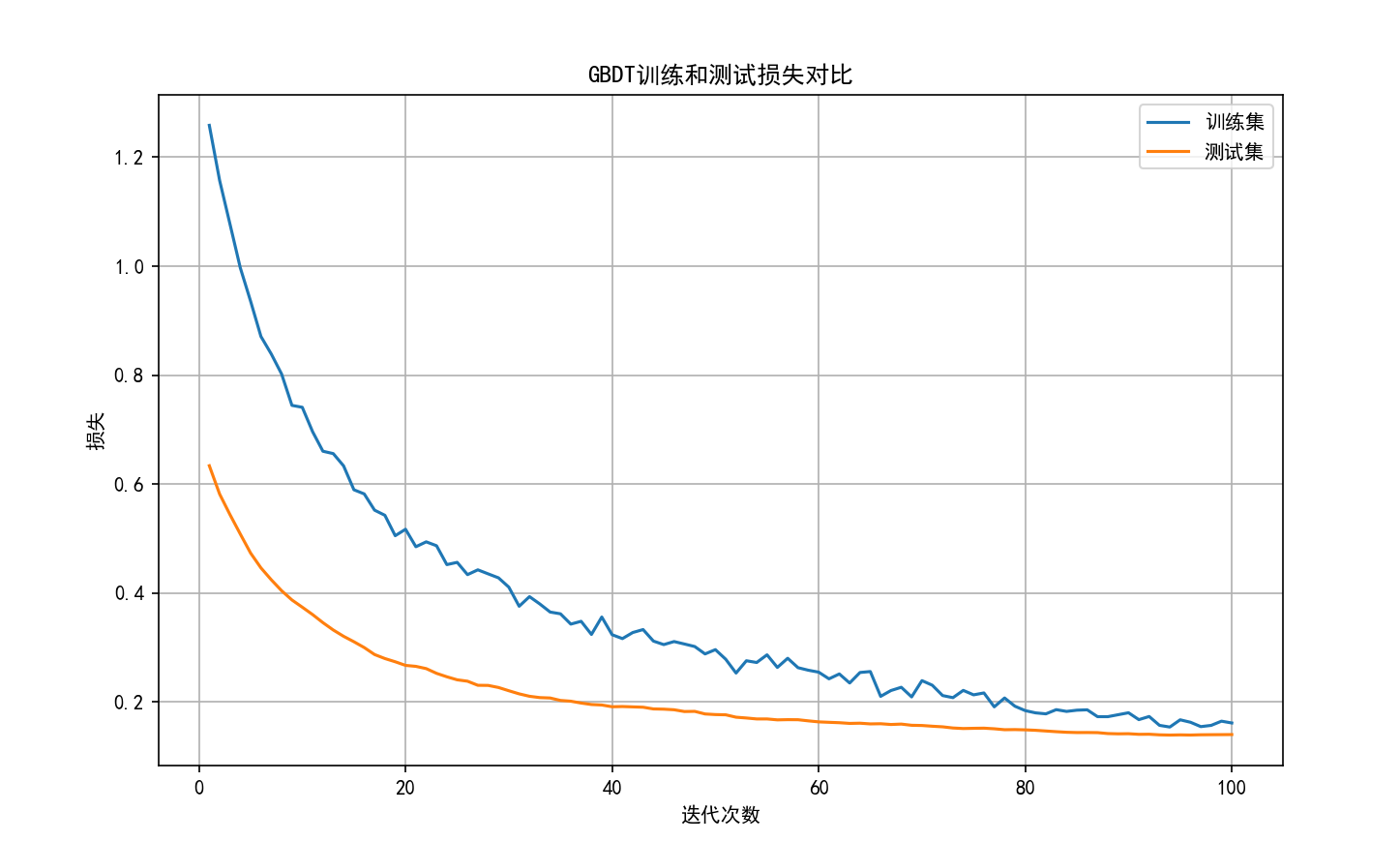
# 额外：绘制训练集损失和测试集损失的对比
plt.figure(figsize=(10, 6))
plt.plot(np.arange(gbdt.n_estimators) + 1, gbdt.train_score_, label='训练集')
plt.plot(np.arange(gbdt.n_estimators) + 1, test_deviance, label='测试集')
plt.xlabel('迭代次数')
plt.ylabel('损失')
plt.title('GBDT训练和测试损失对比')
plt.legend()
plt.grid(True)
plt.show()

程序运行结果如下

4.3 XGBoost实现示例

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
import xgboost as xgb
from sklearn.metrics import accuracy_score, roc_curve, auc, confusion_matrix
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import matplotlib as mpl
from matplotlib.font_manager import FontProperties
import platform
import os
import warnings

# 忽略字体相关警告
warnings.filterwarnings("ignore", category=UserWarning, module="matplotlib")

# 定义更可靠的字体设置函数
def setup_chinese_font():
    system = platform.system()
    
    # 根据操作系统选择合适的字体
    if system == 'Windows':
        font_paths = [
            'C:/Windows/Fonts/simhei.ttf',    # 黑体
            'C:/Windows/Fonts/simsun.ttc',    # 宋体
            'C:/Windows/Fonts/msyh.ttc',      # 微软雅黑
            'C:/Windows/Fonts/simfang.ttf',   # 仿宋
        ]
    elif system == 'Darwin':  # macOS
        font_paths = [
            '/System/Library/Fonts/PingFang.ttc',
            '/Library/Fonts/STHeiti Light.ttc',
            '/Library/Fonts/Songti.ttc',
        ]
    else:  # Linux
        font_paths = [
            '/usr/share/fonts/truetype/wqy/wqy-microhei.ttc',
            '/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc',
            '/usr/share/fonts/truetype/arphic/uming.ttc',
        ]
    
    # 检查字体文件是否存在，选择第一个存在的字体
    for font_path in font_paths:
        if os.path.exists(font_path):
            print(f"使用字体: {font_path}")
            return FontProperties(fname=font_path)
    
    # 如果没有找到任何中文字体，使用系统默认字体并报告
    print("未找到指定的中文字体文件，将尝试使用系统配置的字体")
    return None

# 设置中文字体
chinese_font = setup_chinese_font()

# 配置matplotlib全局字体设置
if chinese_font is not None:
    plt.rcParams['font.family'] = chinese_font.get_family()
    plt.rcParams['font.sans-serif'] = [chinese_font.get_name()] + plt.rcParams['font.sans-serif']
else:
    # 尝试直接设置字体名称
    plt.rcParams['font.sans-serif'] = ['SimHei', 'WenQuanYi Micro Hei', 'Microsoft YaHei', 
                                       'PingFang SC', 'Heiti SC', 'STHeiti', 
                                       'Source Han Sans CN', 'Noto Sans CJK SC', 
                                       'DejaVu Sans', 'Arial']
plt.rcParams['axes.unicode_minus'] = False

# 设置更好看的风格
plt.style.use('ggplot')

# 生成数据
X, y = make_classification(n_samples=1000, n_features=10,
                          n_informative=5, n_redundant=3,
                          random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 将数据转换为DMatrix格式
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)

# 设置参数
params = {
    'objective': 'binary:logistic',
    'eta': 0.1,
    'max_depth': 3,
    'min_child_weight': 1,
    'subsample': 0.8,
    'colsample_bytree': 0.8,
    'lambda': 1,  # L2正则化
    'alpha': 0,   # L1正则化
    'eval_metric': 'error'
}

# 创建字典用于存储评估结果
evals_result = {}

# 训练模型
num_round = 100
print("训练XGBoost模型中...")
xgb_model = xgb.train(
    params, 
    dtrain, 
    num_round, 
    evals=[(dtrain, 'train'), (dtest, 'test')],
    evals_result=evals_result,
    early_stopping_rounds=10, 
    verbose_eval=10
)

# 预测
y_pred = xgb_model.predict(dtest)
y_pred_binary = np.array([1 if p > 0.5 else 0 for p in y_pred])
accuracy = accuracy_score(y_test, y_pred_binary)
print(f"XGBoost准确率: {accuracy:.4f}")

# 辅助函数：为每个绘图添加字体属性
def add_font_to_texts(ax):
    if chinese_font is not None:
        for text in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
                    ax.get_xticklabels() + ax.get_yticklabels()):
            text.set_fontproperties(chinese_font)

# 分成两个独立的图而不是子图，以避免重叠问题
# 图1：特征重要性 - Weight (单独绘制在一个图上)
plt.figure(figsize=(10, 8))
feature_importance = xgb_model.get_score(importance_type='weight')
features = list(feature_importance.keys())
importance_weight = list(feature_importance.values())
# 按重要性排序
sorted_idx = np.argsort(importance_weight)
plt.barh(range(len(sorted_idx)), [importance_weight[i] for i in sorted_idx], align='center')
plt.yticks(range(len(sorted_idx)), [features[i] for i in sorted_idx])
plt.title('特征重要性 (权重)', fontsize=14)
plt.xlabel('权重', fontsize=12)
if chinese_font:
    plt.title('特征重要性 (权重)', fontproperties=chinese_font, fontsize=14)
    plt.xlabel('权重', fontproperties=chinese_font, fontsize=12)
    plt.yticks(fontproperties=chinese_font)
plt.tight_layout()
plt.savefig('特征重要性_权重.png', dpi=300, bbox_inches='tight')
plt.show()

# 图2：特征重要性 - Gain (单独绘制在一个图上)
plt.figure(figsize=(10, 8))
feature_importance = xgb_model.get_score(importance_type='gain')
features = list(feature_importance.keys())
importance_gain = list(feature_importance.values())
# 按重要性排序
sorted_idx = np.argsort(importance_gain)
plt.barh(range(len(sorted_idx)), [importance_gain[i] for i in sorted_idx], align='center')
plt.yticks(range(len(sorted_idx)), [features[i] for i in sorted_idx])
plt.title('特征重要性 (增益值)', fontsize=14)
plt.xlabel('增益值', fontsize=12)
if chinese_font:
    plt.title('特征重要性 (增益值)', fontproperties=chinese_font, fontsize=14)
    plt.xlabel('增益值', fontproperties=chinese_font, fontsize=12)
    plt.yticks(fontproperties=chinese_font)
plt.tight_layout()
plt.savefig('特征重要性_增益值.png', dpi=300, bbox_inches='tight')
plt.show()

# 创建2x2布局的图表，包含ROC曲线、误差变化、混淆矩阵和概率分布
fig, axes = plt.subplots(2, 2, figsize=(16, 14))

# 1. 绘制ROC曲线
fpr, tpr, _ = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
axes[0, 0].plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.3f})')
axes[0, 0].plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
axes[0, 0].set_xlim([0.0, 1.0])
axes[0, 0].set_ylim([0.0, 1.05])
axes[0, 0].set_xlabel('假阳性率', fontsize=12)
axes[0, 0].set_ylabel('真阳性率', fontsize=12)
axes[0, 0].set_title('ROC曲线', fontsize=14)
axes[0, 0].legend(loc="lower right")
if chinese_font:
    axes[0, 0].set_xlabel('假阳性率', fontproperties=chinese_font, fontsize=12)
    axes[0, 0].set_ylabel('真阳性率', fontproperties=chinese_font, fontsize=12)
    axes[0, 0].set_title('ROC曲线', fontproperties=chinese_font, fontsize=14)
    for text in axes[0, 0].get_legend().get_texts():
        text.set_fontproperties(chinese_font)

# 2. 训练过程中的误差变化
epochs = len(evals_result['train']['error'])
x_axis = range(0, epochs)
axes[0, 1].plot(x_axis, evals_result['train']['error'], label='训练集误差', marker='o', markersize=3)
axes[0, 1].plot(x_axis, evals_result['test']['error'], label='测试集误差', marker='s', markersize=3)
axes[0, 1].grid(True)
axes[0, 1].legend()
axes[0, 1].set_xlabel('迭代次数', fontsize=12)
axes[0, 1].set_ylabel('分类误差', fontsize=12)
axes[0, 1].set_title('XGBoost训练过程误差变化', fontsize=14)
if chinese_font:
    axes[0, 1].set_xlabel('迭代次数', fontproperties=chinese_font, fontsize=12)
    axes[0, 1].set_ylabel('分类误差', fontproperties=chinese_font, fontsize=12)
    axes[0, 1].set_title('XGBoost训练过程误差变化', fontproperties=chinese_font, fontsize=14)
    for text in axes[0, 1].get_legend().get_texts():
        text.set_fontproperties(chinese_font)

# 3. 混淆矩阵
cm = confusion_matrix(y_test, y_pred_binary)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', cbar=False, ax=axes[1, 0])
axes[1, 0].set_xlabel('预测标签', fontsize=12)
axes[1, 0].set_ylabel('真实标签', fontsize=12)
axes[1, 0].set_title('混淆矩阵', fontsize=14)
if chinese_font:
    axes[1, 0].set_xlabel('预测标签', fontproperties=chinese_font, fontsize=12)
    axes[1, 0].set_ylabel('真实标签', fontproperties=chinese_font, fontsize=12)
    axes[1, 0].set_title('混淆矩阵', fontproperties=chinese_font, fontsize=14)

# 4. 预测概率分布
axes[1, 1].hist(y_pred, bins=20, alpha=0.5, label='所有样本')
axes[1, 1].hist(y_pred[y_test==1], bins=20, alpha=0.5, label='正样本')
axes[1, 1].hist(y_pred[y_test==0], bins=20, alpha=0.5, label='负样本')
axes[1, 1].set_xlabel('预测概率', fontsize=12)
axes[1, 1].set_ylabel('样本数量', fontsize=12)
axes[1, 1].set_title('预测概率分布', fontsize=14)
axes[1, 1].legend()
if chinese_font:
    axes[1, 1].set_xlabel('预测概率', fontproperties=chinese_font, fontsize=12)
    axes[1, 1].set_ylabel('样本数量', fontproperties=chinese_font, fontsize=12)
    axes[1, 1].set_title('预测概率分布', fontproperties=chinese_font, fontsize=14)
    for text in axes[1, 1].get_legend().get_texts():
        text.set_fontproperties(chinese_font)

plt.tight_layout(pad=3.0)  # 增加子图之间的间距
plt.savefig('xgboost模型评估.png', dpi=300, bbox_inches='tight')
plt.show()

# 计算和展示主要评估指标
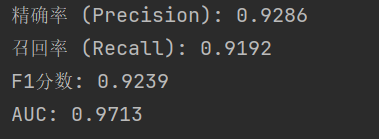
from sklearn.metrics import precision_score, recall_score, f1_score, precision_recall_curve

precision = precision_score(y_test, y_pred_binary)
recall = recall_score(y_test, y_pred_binary)
f1 = f1_score(y_test, y_pred_binary)

print(f"精确率 (Precision): {precision:.4f}")
print(f"召回率 (Recall): {recall:.4f}")
print(f"F1分数: {f1:.4f}")
print(f"AUC: {roc_auc:.4f}")

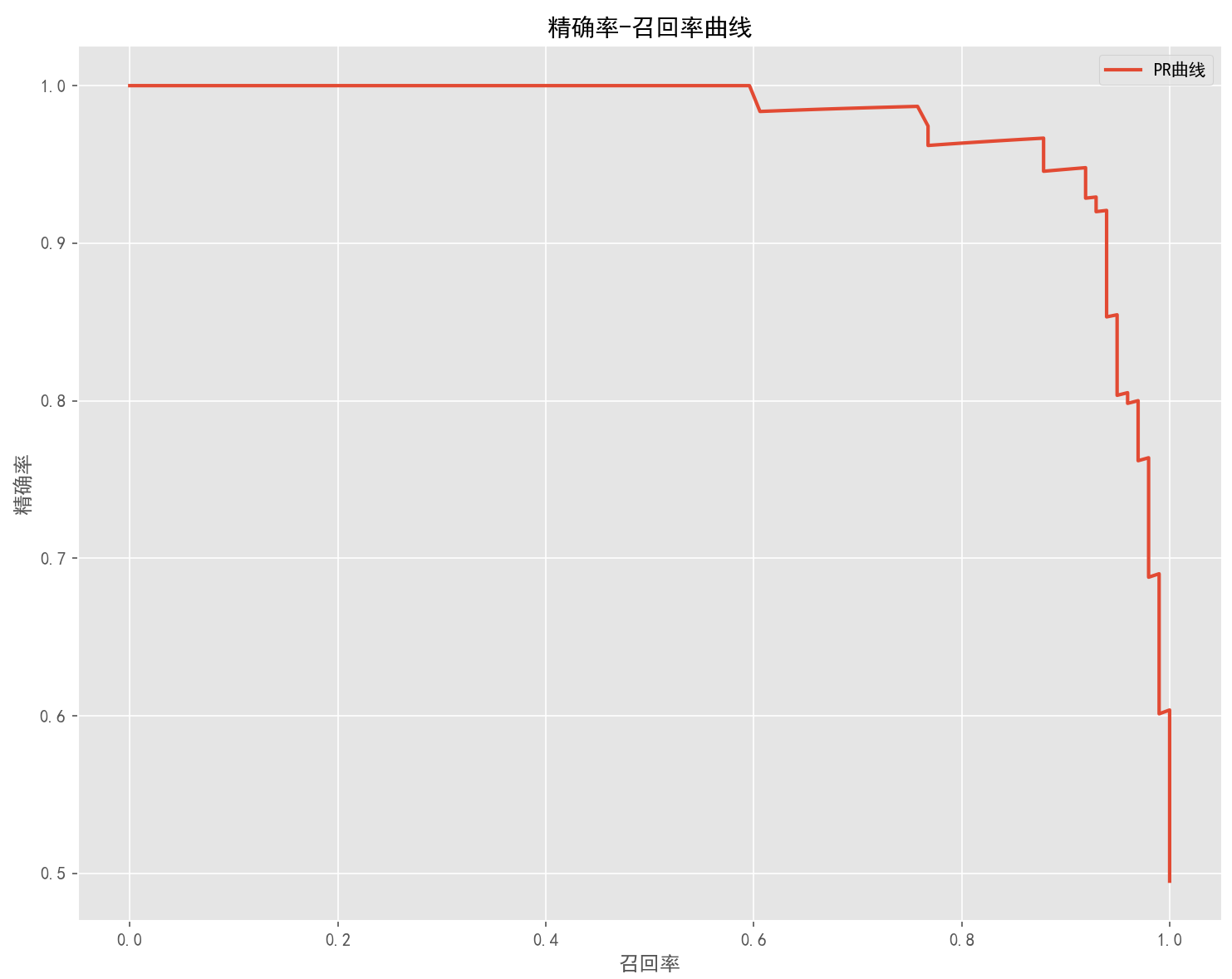
# 绘制精确率-召回率曲线
plt.figure(figsize=(10, 8))
precision_curve, recall_curve, thresholds = precision_recall_curve(y_test, y_pred)
plt.plot(recall_curve, precision_curve, lw=2, label='PR曲线')
plt.grid(True)
plt.xlabel('召回率', fontsize=12)
plt.ylabel('精确率', fontsize=12)
plt.title('精确率-召回率曲线', fontsize=14)
plt.legend()
if chinese_font:
    plt.xlabel('召回率', fontproperties=chinese_font, fontsize=12)
    plt.ylabel('精确率', fontproperties=chinese_font, fontsize=12)
    plt.title('精确率-召回率曲线', fontproperties=chinese_font, fontsize=14)
    for text in plt.legend().get_texts():
        text.set_fontproperties(chinese_font)
plt.tight_layout()
plt.savefig('xgboost_PR曲线.png', dpi=300, bbox_inches='tight')
plt.show()

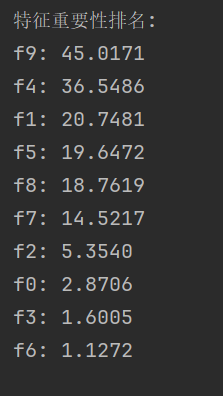
# 特征重要性分析 - 输出具体数值
print("\n特征重要性排名:")
importance = xgb_model.get_score(importance_type='gain')
sorted_importance = sorted(importance.items(), key=lambda x: x[1], reverse=True)
for feature, score in sorted_importance:
    print(f"{feature}: {score:.4f}")

程序运行结果如下：

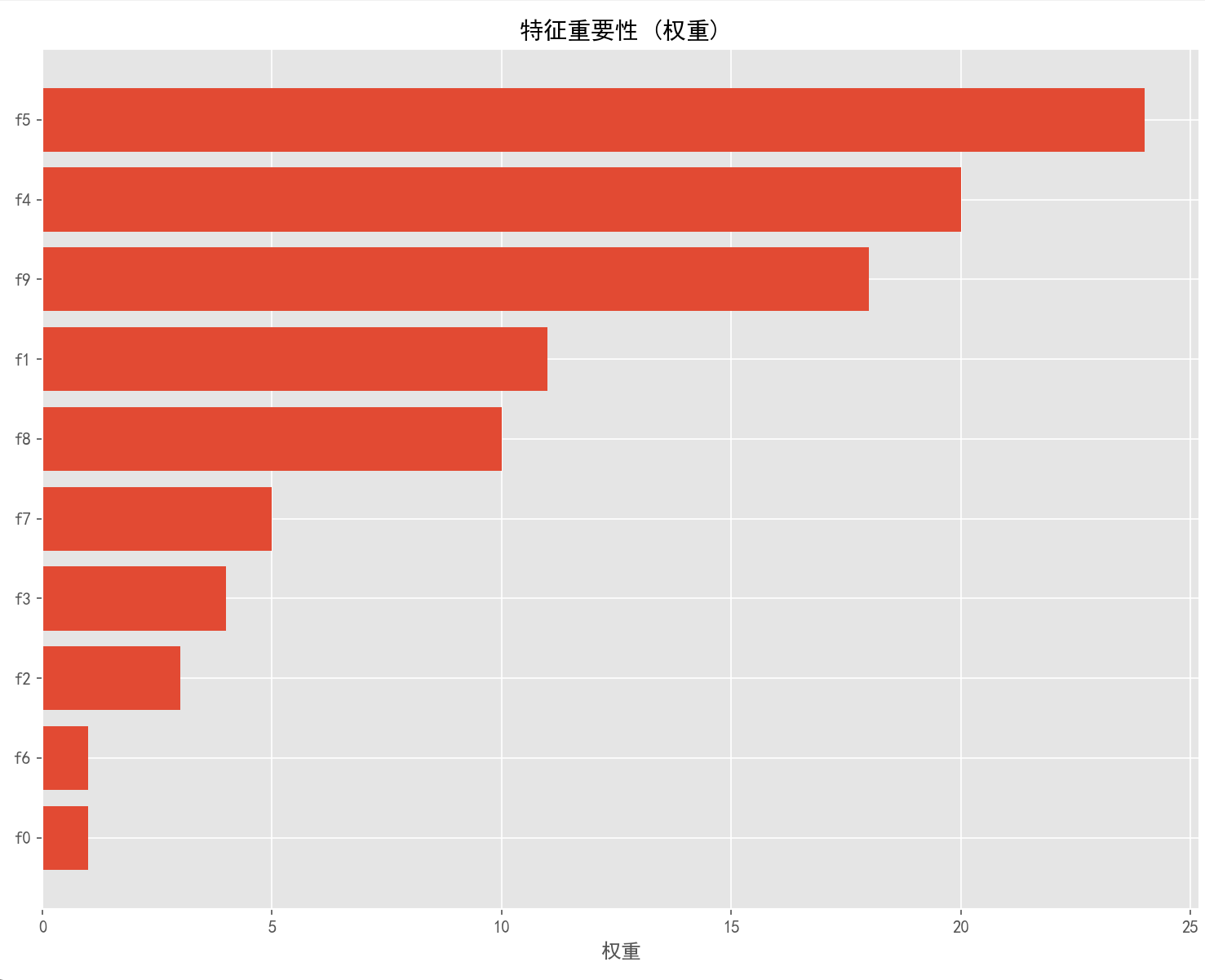
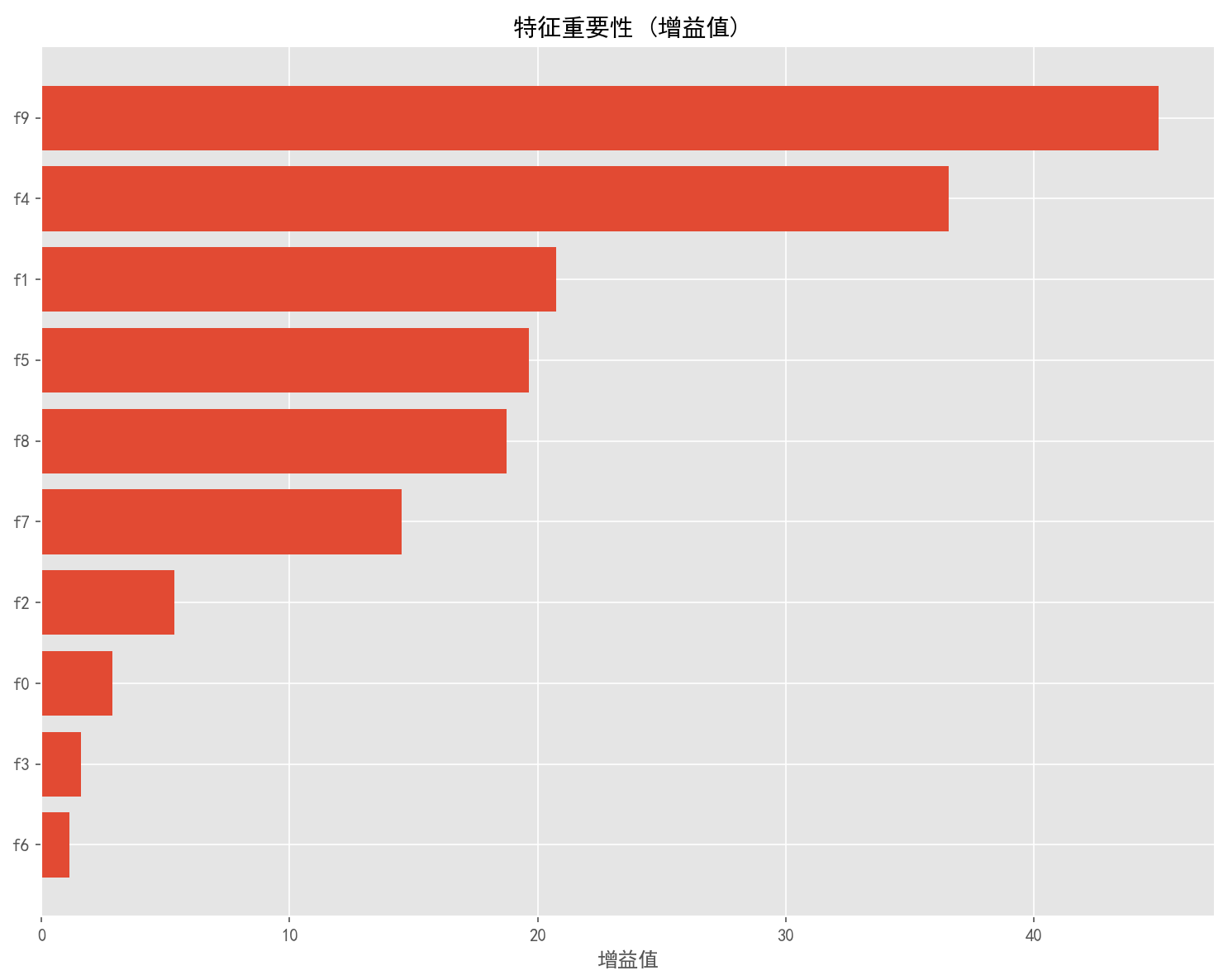
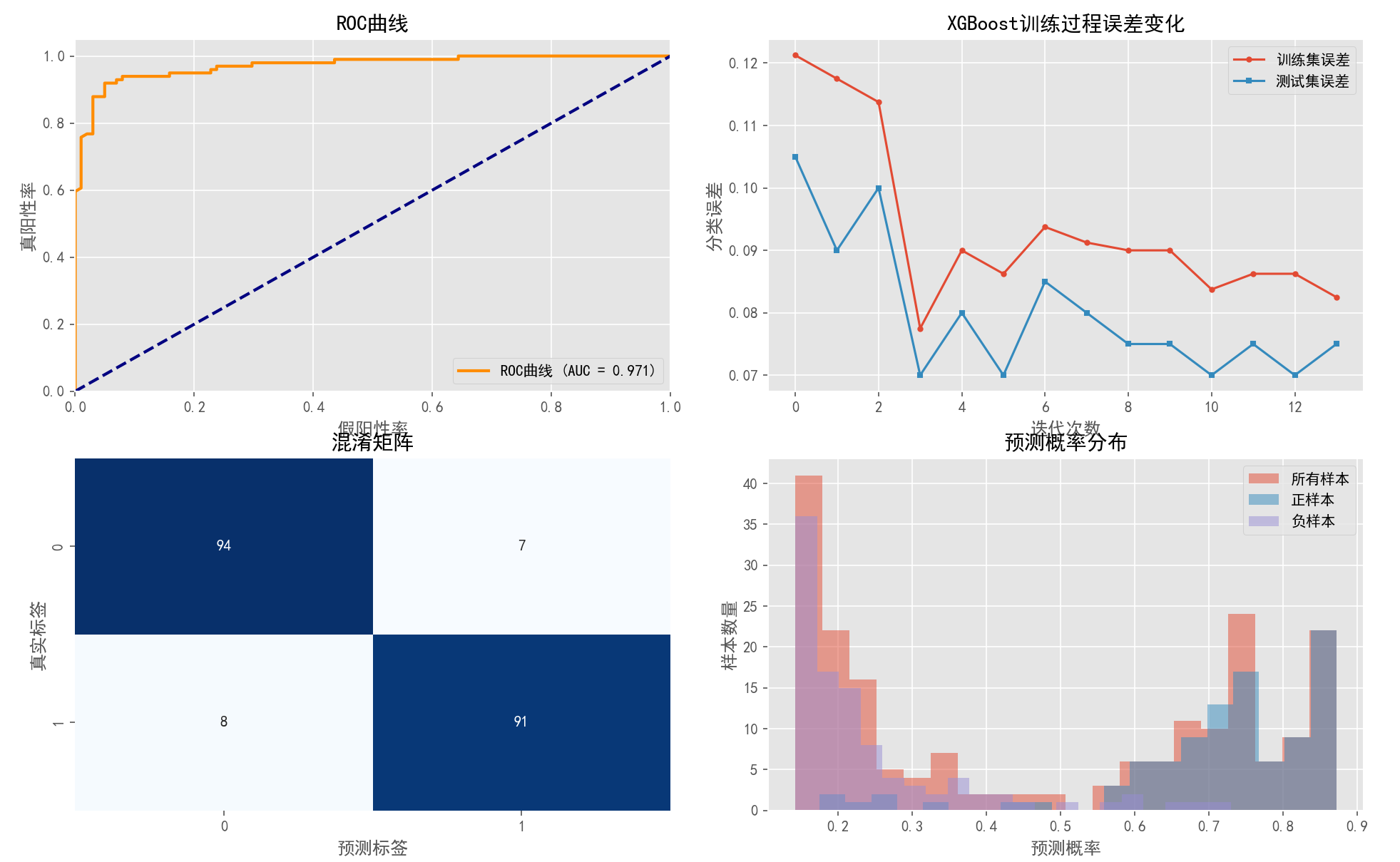
五、Python代码实现集成学习与梯度提升决策树的实验

（一）实验内容和实验步骤

1. 实验准备与环境设置

1.1 导入必要库

首先导入所需的Python库，包括数据处理（NumPy）、可视化（Matplotlib、Seaborn）、机器学习模型（scikit-learn）等。特别注意导入了集成学习相关的类，如BaggingClassifier、RandomForestClassifier、AdaBoostClassifier等。

1.2 环境配置

（1）创建结果保存目录（ensemble_learning_results）。

（2）配置matplotlib以支持中文显示。

（3）设置临时文件夹和警告抑制。

（4）生成时间戳用于唯一命名图片文件。

1.3 数据集生成

使用`make_classification`函数创建一个具有以下特性的合成分类数据集：

（1） 1000个样本。

（2） 16维特征。

（3） 5个信息特征和2个冗余特征。

（4） 2个类别。

（5） 10%的标签噪声。

然后将数据集分为80%训练集和20%测试集，用于后续算法评估。

2. Bagging和随机森林算法实现

2.1 RandomForest类实现

理论基础

Bagging（Bootstrap Aggregating）通过对训练集进行自助采样（有放回抽样），构建多个训练子集，然后在每个子集上训练一个基本分类器。随机森林是Bagging的一个特例，它使用决策树作为基学习器，并在树的生长过程中随机选择特征子集。

数学公式：

对于分类问题，最终预测为： $H(x) = \arg\max_y \sum_{i=1}^T \mathbf{1}(h_i(x) = y)$ 。

Bagging和随机森林的主要区别在于：Bagging使用所有特征构建决策树，而随机森林在每个节点只使用特征的随机子集（通常为 $\sqrt{d}$ 个）。

代码实现

`RandomForest`类包含：

初始化：

def __init__(self, n_trees=10, max_features='sqrt'):

    self.n_trees = n_trees  # 树的数量

    self.oob_score = 0      # 袋外样本评分

    self.trees = [DTC(max_features=max_features) for _ in range(n_trees)]  # 决策树列表

训练过程（fit方法）：

（1）对每棵树进行自助采样训练。

（2）记录每个样本的袋外预测。

（3）计算袋外样本的准确率作为OOB分数。

预测过程：

（1）获取每棵树的预测概率。

（2）计算平均概率。

（3）返回概率最高的类别。

2.2 Bagging与随机森林对比实验

在相同的数据集上分别训练Bagging和随机森林模型，对比不同树数量（1到100棵树）下的训练集性能和OOB分数：

Bagging：`max_features=None`（使用全部特征）

随机森林：`max_features='sqrt'`（使用特征数量的平方根）

实验结果通过曲线图可视化，展示了：

（1）随着树数量增加，两种算法的性能均提高。

（2） Bagging在训练集上表现更好但可能过拟合。

（3）随机森林OOB分数通常高于Bagging。

2.3 与sklearn库实现对比

训练scikit-learn的BaggingClassifier和RandomForestClassifier与手动实现进行对比，验证实现的正确性。

3. Stacking（堆叠集成）算法实现

3.1 理论基础

Stacking通过训练一个元学习器（meta-learner）来组合多个基学习器的预测结果。为了防止过拟合，通常使用K折交叉验证生成元特征。

数学原理：

对于 $k$ 个基学习器，第 $j$ 个基学习器的预测为： $z_{ij} = h_j(x_i)$

元学习器的输入为： $z_i = (z_{i1}, z_{i2}, ..., z_{ik})$

最终预测为： $H(x) = h_{meta}(z(x))$

3.2 实现步骤

SimpleNeuralNetwork类：

实现了一个简单的神经网络，用作元分类器

包含一个隐藏层，使用sigmoid激活函数

实现了前向传播和反向传播算法

StackingClassifier类：

class StackingClassifier():

    def __init__(self, classifiers, meta_classifier, concat_feature=False, kfold=5):

        # 初始化参数和基分类器

训练过程(fit方法)：

（1）对每个基分类器:

a. 使用K折交叉验证生成元特征。

b. 在每一折上训练基分类器。

c. 在验证集上预测，获得概率预测作为元特征。

（2）将所有元特征合并（可选添加原始特征）。

（3）使用元特征训练元分类器。

预测过程：

（1）生成测试数据的元特征。

（2）使用元分类器进行最终预测。

3.3 实验分析

实验评估了使用不同元分类器（逻辑回归、决策树、神经网络）的堆叠模型性能，以及是否添加原始特征的影响。

4. AdaBoost算法实现

4.1 理论基础

AdaBoost是一种自适应增强算法，通过迭代训练一系列弱分类器，每次关注上一轮分类错误的样本，最终加权组合所有弱分类器。

关键数学公式：

计算基分类器权重： $\alpha_t = \frac{1}{2} \ln \left( \frac{1-\epsilon_t}{\epsilon_t} \right)$ ，其中 $\epsilon_t$ 是加权错误率

更新样本权重： $w_{t+1}(i) = \frac{w_t(i)}{Z_t} \exp(-\alpha_t y_i h_t(x_i))$

最终分类器： $H(x) = \text{sign}\left( \sum_{t=1}^T \alpha_t h_t(x) \right)$

4.2 实现细节

DecisionStump类：

class DecisionStump:

    def __init__(self):

        self.polarity = 1  # 划分方向（+1或-1）

        self.feature_idx = None  # 使用哪个特征

        self.threshold = None  # 阈值

        self.alpha = None  # 分类器权重

AdaBoost类：

class AdaBoost:

    def __init__(self, n_estimators=50):

        self.n_estimators = n_estimators  # 基分类器数量

        self.stumps = []  # 存储所有决策树桩

训练过程(fit方法)：

（1）初始化样本权重为均匀分布。

（2）对每次迭代:

a. 在所有特征和阈值组合中找到最佳决策树桩（最小加权错误率）。

b. 计算该分类器的权重alpha。

c. 更新样本权重（提高错分样本的权重）。

d. 保存基分类器。

预测过程：

（1）计算所有决策树桩的加权和。

（2）返回符号值（正负表示类别）。

4.3 评估与可视化

实验包括了多种评估方式：

（1）在测试集上计算准确率。

（2）可视化样本权重变化过程。

（3）展示基分类器错误率和权重变化。

（4）可视化决策边界的演变过程。

（5）在不同复杂度数据集上的表现分析。

5. XGBoost算法实现

5.1 理论基础

XGBoost（Extreme Gradient Boosting）是梯度提升决策树（GBDT）的高效实现，它通过梯度和二阶导数（Hessian）来指导优化。

关键数学公式：

目标函数： $\mathcal{L}(\phi) = \sum_i l(y_i, \hat{y}_i) + \sum_k \Omega(f_k)$

使用泰勒展开近似： $\mathcal{L}^{(t)} \approx \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)] + \Omega(f_t)$

其中 $g_i$ 和 $h_i$ 分别是损失函数的一阶和二阶导数

5.2 实现细节

XGBoostTree类：处理单棵树的构建和预测

class XGBoostTree:

    def __init__(self, max_depth=3, min_child_weight=1, gamma=0):

        # 初始化树参数

构建树过程(_build_tree方法)：

（1）计算当前节点的梯度和Hessian。

（2）如果达到停止条件（最大深度或最小样本权重），创建叶节点。

（3）在所有特征和阈值组合中找到最佳分裂点（最大增益）。

（4）递归构建左右子树。

SimpleXGBoost类：管理多棵树的训练和预测

class SimpleXGBoost:

    def __init__(self, n_estimators=10, learning_rate=0.1, max_depth=3, min_child_weight=1, gamma=0):

        # 初始化参数

训练过程(fit方法)：

（1）初始预测值为目标均值。

（2）对每次迭代:

a. 计算当前梯度和Hessian。

b. 构建新树拟合这些梯度。

c. 以学习率为步长更新预测值。

d. 保存树模型。

预测过程：

（1）从初始预测值开始

（2）累加每棵树乘以学习率的预测值

5.3 实验分析

实验包括：

（1）与sklearn的GradientBoostingRegressor对比性能。

（2）可视化特征重要性。

（3）分析学习率对性能的影响。

（4）分析树深度对性能的影响。

（5）残差图和预测值vs实际值对比。

6. 性能评估与比较

6.1 评估指标

分类任务：准确率（Accuracy）

回归任务：R²决定系数（越接近1越好）

6.2 集成学习算法比较

对所有算法进行了统一数据集上的性能对比，包括：

（1）手动实现的随机森林和AdaBoost。

（2） scikit-learn的RandomForestClassifier、AdaBoostClassifier、GradientBoostingClassifier和BaggingClassifier。

6.3 超参数调优

对RandomForestClassifier进行了网格搜索（GridSearchCV），优化：

n_estimators：树的数量

max_features：每个节点考虑的特征数

max_depth：树的最大深度

6.4 最终模型比较

比较了各种集成模型在测试集上的性能，并通过条形图可视化结果，将性能最好的模型突出显示。

7. 结果分析与可视化

7.1 随机森林分析

特征重要性可视化：识别模型中最重要的特征

混淆矩阵：展示分类错误的类型和分布

分类报告：包括精确率、召回率和F1分数

7.2 AdaBoost详细分析

样本权重变化过程：展示算法如何关注困难样本

基学习器错误率和权重变化：展示弱学习器如何组合成强学习器

决策边界演变：可视化模型学习过程

不同数据集性能：测试模型在不同复杂度数据上的表现

7.3 XGBoost分析

特征重要性：展示每个特征对预测的贡献

超参数敏感性分析：学习率和树深度的影响

残差分析：检查模型预测误差的分布

（二）Python代码完整实现

完整的Python代码如下：

print('集成学习与梯度提升决策树的实验开始')
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
from sklearn.datasets import make_classification, make_friedman1
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.tree import DecisionTreeRegressor as DTR
from sklearn.linear_model import LogisticRegression as LR
from sklearn.neighbors import KNeighborsClassifier as KNC
from sklearn.neighbors import KNeighborsRegressor as KNR
from sklearn.linear_model import LinearRegression as LR_Reg
from sklearn.model_selection import KFold
from sklearn.base import clone
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
from sklearn.model_selection import GridSearchCV, cross_val_score
import seaborn as sns
from sklearn.datasets import make_circles, make_moons, make_gaussian_quantiles
# 添加缺少的导入
from sklearn.ensemble import (
    BaggingClassifier, RandomForestClassifier, AdaBoostClassifier,
    GradientBoostingClassifier, GradientBoostingRegressor
)
import warnings
import tempfile
import os
import matplotlib as mpl
import datetime

warnings.filterwarnings("ignore", message="Font.*glyph for.*")
# 创建保存图片的目录
results_dir = "ensemble_learning_results"
if not os.path.exists(results_dir):
    os.makedirs(results_dir)

# 获取当前时间戳，用于图像文件命名，避免覆盖
timestamp = datetime.datetime.now().strftime("%Y%m%d_%H%M%S")

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 为joblib设置临时文件夹到只包含ASCII字符的路径
temp_folder = tempfile.mkdtemp(prefix='sklearn_')
os.environ['JOBLIB_TEMP_FOLDER'] = temp_folder

# 忽略警告
warnings.filterwarnings('ignore')

print('动手实现决策树的bagging算法和随机森林算法')
# 创建随机数据集
X, y = make_classification(
    n_samples=1000,  # 数据集大小
    n_features=16,  # 特征数，即特征维度
    n_informative=5,  # 有效特征个数
    n_redundant=2,  # 冗余特征个数，为有效特征的随即线性组合
    n_classes=2,  # 类别数
    flip_y=0.1,  # 类别随机的样本个数，该值越大，分类越困难
    random_state=0  # 随机种子
)

print(f"数据集形状: {X.shape}, 类别分布: {np.bincount(y)}")

# 划分训练集和测试集 - 这是主要数据集，用于大多数实验
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)


# 定义随机森林类
class RandomForest():
    def __init__(self, n_trees=10, max_features='sqrt'):
        self.n_trees = n_trees
        self.oob_score = 0
        self.trees = [DTC(max_features=max_features) for _ in range(n_trees)]

    # 用X和y训练模型
    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.n_classes = np.unique(y).shape[0]
        # 集成模型的预测，累加单个模型预测的分类概率，再取较大值作为最终分类
        ensemble = np.zeros((n_samples, self.n_classes))

        for tree in self.trees:
            # 自举采样，该采样允许重复
            idx = np.random.randint(0, n_samples, n_samples)
            # 没有被采到的样本
            unsampled_mask = np.bincount(idx, minlength=n_samples) == 0
            unsampled_idx = np.arange(n_samples)[unsampled_mask]
            # 训练当前决策树
            tree.fit(X[idx], y[idx])
            # 累加决策树对OOB样本的预测
            if len(unsampled_idx) > 0:  # 确保有OOB样本
                ensemble[unsampled_idx] += tree.predict_proba(X[unsampled_idx])

        # 计算OOB分数，由于是分类问题，我们用准确率来衡量
        # 确保所有样本至少被一个模型作为OOB样本
        valid_samples = np.sum(ensemble, axis=1) > 0
        if np.any(valid_samples):
            self.oob_score = np.mean(y[valid_samples] == np.argmax(ensemble[valid_samples], axis=1))
        else:
            self.oob_score = 0

    # 预测类别
    def predict(self, X):
        proba = self.predict_proba(X)
        return np.argmax(proba, axis=1)

    def predict_proba(self, X):
        # 取所有决策树预测概率的平均
        ensemble = np.mean([tree.predict_proba(X) for tree in self.trees], axis=0)
        return ensemble

    # 计算准确率
    def score(self, X, y):
        return np.mean(y == self.predict(X))


# 算法测试与可视化
num_trees = np.arange(1, 101, 5)
np.random.seed(0)
plt.figure(figsize=(10, 6))

# bagging算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:
    for n_tree in pbar:
        rf = RandomForest(n_trees=n_tree, max_features=None)
        rf.fit(X, y)
        train_score.append(rf.score(X, y))
        oob_score.append(rf.oob_score)
        pbar.set_postfix({
            'n_tree': n_tree,
            'train_score': train_score[-1],
            'oob_score': oob_score[-1]
        })
plt.plot(num_trees, train_score, color='blue', label='bagging_train_score')
plt.plot(num_trees, oob_score, color='blue', ls='-.', label='bagging_oob_score')

# 随机森林算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:
    for n_tree in pbar:
        rf = RandomForest(n_trees=n_tree, max_features='sqrt')
        rf.fit(X, y)
        train_score.append(rf.score(X, y))
        oob_score.append(rf.oob_score)
        pbar.set_postfix({
            'n_tree': n_tree,
            'train_score': train_score[-1],
            'oob_score': oob_score[-1]
        })
plt.plot(num_trees, train_score, color='red', ls='--', label='random_forest_train_score')
plt.plot(num_trees, oob_score, color='red', ls=':', label='random_forest_oob_score')

plt.ylabel('Score')
plt.xlabel('Number of trees')
plt.legend()
plt.title('Bagging vs Random Forest (手动实现)')
plt.grid(True, linestyle='--', alpha=0.7)

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_bagging_vs_rf.png"), dpi=300, bbox_inches='tight')
plt.show()

# 使用sklearn库进行对比
print('用sklearn中的bagging算法和随机森林算法在同样的数据集上进行测试，与动手实现的算法的结果进行比较，验证实验的正确性。')

# 在新版本sklearn中，base_estimator已被废弃，改用estimator参数
bc = BaggingClassifier(estimator=DTC(), n_estimators=100, oob_score=True, random_state=0)
bc.fit(X, y)
print('bagging：', bc.oob_score_)

rfc = RandomForestClassifier(n_estimators=100, max_features='sqrt', oob_score=True, random_state=0)
rfc.fit(X, y)
print('随机森林：', rfc.oob_score_)

# ============= 自定义神经网络元分类器 =============
print('\n自定义神经网络作为元分类器')


class SimpleNeuralNetwork:
    def __init__(self, input_size, hidden_size=10, output_size=2, learning_rate=0.01, epochs=100):
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.learning_rate = learning_rate
        self.epochs = epochs

        # 初始化权重
        self.W1 = np.random.randn(input_size, hidden_size) * 0.01
        self.b1 = np.zeros((1, hidden_size))
        self.W2 = np.random.randn(hidden_size, output_size) * 0.01
        self.b2 = np.zeros((1, output_size))

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-np.clip(x, -500, 500)))

    def softmax(self, x):
        exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
        return exp_x / np.sum(exp_x, axis=1, keepdims=True)

    def forward(self, X):
        # 前向传播
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = self.sigmoid(self.z1)
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = self.softmax(self.z2)
        return self.a2

    def fit(self, X, y):
        # 将y转换为one-hot编码
        y_onehot = np.zeros((len(y), self.output_size))
        for i in range(len(y)):
            y_onehot[i, y[i]] = 1

        # 训练
        for _ in range(self.epochs):
            # 前向传播
            output = self.forward(X)

            # 反向传播
            delta2 = output - y_onehot
            dW2 = np.dot(self.a1.T, delta2)
            db2 = np.sum(delta2, axis=0, keepdims=True)

            delta1 = np.dot(delta2, self.W2.T) * (self.a1 * (1 - self.a1))
            dW1 = np.dot(X.T, delta1)
            db1 = np.sum(delta1, axis=0)

            # 更新权重
            self.W2 -= self.learning_rate * dW2
            self.b2 -= self.learning_rate * db2
            self.W1 -= self.learning_rate * dW1
            self.b1 -= self.learning_rate * db1

    def predict_proba(self, X):
        return self.forward(X)

    def predict(self, X):
        return np.argmax(self.predict_proba(X), axis=1)

    def score(self, X, y):
        return np.mean(self.predict(X) == y)


# ============= 堆垛算法 =============
print('\n动手实现堆垛算法')


# 堆垛分类器
class StackingClassifier():
    def __init__(
            self,
            classifiers,  # 基分类器
            meta_classifier,  # 元分类器
            concat_feature=False,  # 是否将原始样本拼接在新数据上
            kfold=5  # K折交叉验证
    ):
        self.classifiers = classifiers
        self.meta_classifier = meta_classifier
        self.concat_feature = concat_feature
        self.kf = KFold(n_splits=kfold)
        # 为了在测试时计算平均，我们需要保留每个分类器
        self.k_fold_classifiers = []

    def fit(self, X, y):
        # 用X和y训练基分类器和元分类器
        n_samples, n_features = X.shape
        self.n_classes = np.unique(y).shape[0]

        if self.concat_feature:
            features = X
        else:
            features = np.zeros((n_samples, 0))
        for classifier in self.classifiers:
            self.k_fold_classifiers.append([])
            # 训练每个基分类器
            predict_proba = np.zeros((n_samples, self.n_classes))
            for train_idx, test_idx in self.kf.split(X):
                # 交叉验证
                clf = clone(classifier)
                clf.fit(X[train_idx], y[train_idx])
                predict_proba[test_idx] = clf.predict_proba(X[test_idx])  # 修正的行
                self.k_fold_classifiers[-1].append(clf)  # 分成独立一行
            features = np.concatenate([features, predict_proba], axis=-1)
        # 训练元分类器
        self.meta_classifier.fit(features, y)


    def _get_features(self, X):
        # 计算输入X的特征
        if self.concat_feature:
            features = X
        else:
            features = np.zeros((X.shape[0], 0))
        for k_classifiers in self.k_fold_classifiers:
            k_feat = np.mean([clf.predict_proba(X) for clf in k_classifiers], axis=0)
            features = np.concatenate([features, k_feat], axis=-1)
        return features

    def predict(self, X):
        return self.meta_classifier.predict(self._get_features(X))

    def score(self, X, y):
        return np.mean(self.predict(X) == y)


# 基分类器训练 - 确保使用X_train和y_train来训练基分类器
rf = RandomForestClassifier(n_estimators=10, max_features='sqrt', random_state=0).fit(X_train, y_train)
knc = KNC().fit(X_train, y_train)
# 避免multi_class警告
lr = LR(solver='liblinear', random_state=0).fit(X_train, y_train)
print('随机森林：', rf.score(X_test, y_test))
print('KNN：', knc.score(X_test, y_test))
print('逻辑斯谛回归：', lr.score(X_test, y_test))

# 元分类器
meta_lr = LR(solver='liblinear', random_state=0)

# 使用逻辑回归作为元分类器的堆垛
sc = StackingClassifier([rf, knc, lr], meta_lr, concat_feature=False)
sc.fit(X_train, y_train)
print('Stacking分类器 (逻辑回归元分类器)：', sc.score(X_test, y_test))

# 使用神经网络作为元分类器的堆垛
n_features = X_train.shape[1]
n_classes = len(np.unique(y_train))
meta_nn = SimpleNeuralNetwork(input_size=n_classes * 3, hidden_size=10, output_size=n_classes)
sc_nn = StackingClassifier([rf, knc, lr], meta_nn, concat_feature=False)
sc_nn.fit(X_train, y_train)
print('Stacking分类器 (神经网络元分类器)：', sc_nn.score(X_test, y_test))

# 使用决策树作为元分类器的堆垛
meta_dt = DTC(max_depth=3)
sc_dt = StackingClassifier([rf, knc, lr], meta_dt, concat_feature=False)
sc_dt.fit(X_train, y_train)
print('Stacking分类器 (决策树元分类器)：', sc_dt.score(X_test, y_test))

# 带原始特征的stacking分类器
sc_concat = StackingClassifier([rf, knc, lr], meta_lr, concat_feature=True)
sc_concat.fit(X_train, y_train)
print('带原始特征的Stacking分类器：', sc_concat.score(X_test, y_test))

# ============= 手动实现AdaBoost算法 =============
print('\n动手实现AdaBoost算法')


class DecisionStump:
    """决策树桩作为AdaBoost的基学习器"""

    def __init__(self):
        # 决策树桩的参数
        self.polarity = 1  # 划分方向，取值{+1, -1}
        self.feature_idx = None  # 用于划分的特征索引
        self.threshold = None  # 划分的阈值
        self.alpha = None  # 该分类器在集成中的权重

    def predict(self, X):
        """预测样本的类别

        参数:
        X: 形状为 [n_samples, n_features] 的特征数组

        返回:
        预测结果: 形状为 [n_samples] 的数组，取值为{+1, -1}
        """
        n_samples = X.shape[0]
        X_column = X[:, self.feature_idx]

        # 根据阈值和极性预测类别
        predictions = np.ones(n_samples)
        if self.polarity == 1:
            predictions[X_column < self.threshold] = -1
        else:
            predictions[X_column > self.threshold] = -1

        return predictions


class AdaBoost:
    """AdaBoost集成算法"""

    def __init__(self, n_estimators=50):
        """初始化AdaBoost

        参数:
        n_estimators: 基学习器的数量，即迭代次数M
        """
        self.n_estimators = n_estimators
        self.stumps = []

    def fit(self, X, y):
        """训练AdaBoost模型

        参数:
        X: 形状为 [n_samples, n_features] 的特征数组
        y: 形状为 [n_samples] 的标签数组，取值为{+1, -1}
        """
        n_samples, n_features = X.shape

        # 确保y的值为+1或-1
        y = np.where(y <= 0, -1, 1)

        # 初始化权重为均匀分布
        w = np.ones(n_samples) / n_samples

        # 迭代训练n_estimators个基学习器
        for _ in range(self.n_estimators):
            # 训练基分类器（决策树桩）
            stump = DecisionStump()
            min_error = float('inf')

            # 在每个特征上寻找最佳划分点
            for feature_idx in range(n_features):
                X_column = X[:, feature_idx]
                thresholds = np.unique(X_column)

                for threshold in thresholds:
                    # 尝试两种极性
                    for polarity in [-1, 1]:
                        # 根据当前极性和阈值进行预测
                        predictions = np.ones(n_samples)
                        if polarity == 1:
                            predictions[X_column < threshold] = -1
                        else:
                            predictions[X_column > threshold] = -1

                        # 计算加权错误率
                        misclassified = predictions != y
                        error = np.sum(w * misclassified)

                        # 更新最佳分类器参数
                        if error < min_error:
                            min_error = error
                            stump.polarity = polarity
                            stump.threshold = threshold
                            stump.feature_idx = feature_idx

            # 计算基学习器的权重alpha
            # 避免误差为0导致的除零错误
            epsilon = 1e-10
            min_error = min(max(min_error, epsilon), 1 - epsilon)
            stump.alpha = 0.5 * np.log((1.0 - min_error) / min_error)

            # 获取当前基学习器的预测结果
            predictions = stump.predict(X)

            # 更新样本权重
            w = w * np.exp(-stump.alpha * y * predictions)
            # 归一化权重，使其和为1
            w = w / np.sum(w)

            # 保存基学习器
            self.stumps.append(stump)

    def predict(self, X):
        """使用训练好的模型进行预测

        参数:
        X: 形状为 [n_samples, n_features] 的特征数组

        返回:
        预测类别: 形状为 [n_samples] 的数组，取值为{+1, -1}
        """
        n_samples = X.shape[0]
        # 计算加权和
        y_pred = np.zeros(n_samples)

        # 每个基学习器根据其权重进行投票
        for stump in self.stumps:
            y_pred += stump.alpha * stump.predict(X)

        # 返回符号值
        return np.sign(y_pred)

    def score(self, X, y):
        """计算模型在给定数据上的准确率"""
        y = np.where(y <= 0, -1, 1)  # 确保y的值为+1或-1
        return np.mean(self.predict(X) == y)


# 创建与之前相同特征数的数据集进行AdaBoost测试，避免特征不匹配问题
X_binary, y_binary = make_classification(
    n_samples=1000,
    n_features=16,  # 与主数据集保持一致
    n_informative=8,
    n_redundant=2,
    random_state=42
)
X_train_ada, X_test_ada, y_train_ada, y_test_ada = train_test_split(X_binary, y_binary, test_size=0.2, random_state=42)

# 将y转换为-1和1
y_train_binary = np.where(y_train_ada <= 0, -1, 1)
y_test_binary = np.where(y_test_ada <= 0, -1, 1)

# 手动实现的AdaBoost
adaboost_manual = AdaBoost(n_estimators=50)
adaboost_manual.fit(X_train_ada, y_train_binary)
ada_accuracy = adaboost_manual.score(X_test_ada, y_test_binary)
print(f'手动实现AdaBoost的准确率：{ada_accuracy:.4f}')

# ============= 手动实现XGBoost算法 =============
print('\n动手实现XGBoost算法 (简化版)')


class XGBoostTree:
    """XGBoost中的决策树"""

    def __init__(self, max_depth=3, min_child_weight=1, gamma=0):
        self.max_depth = max_depth
        self.min_child_weight = min_child_weight  # 最小样本权重和
        self.gamma = gamma  # 分裂的正则化系数
        self.tree = {}  # 存储树结构

    def _calculate_gain(self, left_grad_sum, left_hess_sum, right_grad_sum, right_hess_sum, grad_sum, hess_sum):
        # 计算分裂增益
        left_gain = -0.5 * left_grad_sum ** 2 / (left_hess_sum + 1e-16)
        right_gain = -0.5 * right_grad_sum ** 2 / (right_hess_sum + 1e-16)
        root_gain = -0.5 * grad_sum ** 2 / (hess_sum + 1e-16)
        gain = left_gain + right_gain - root_gain - self.gamma
        return gain

    def _calculate_leaf_weight(self, grad_sum, hess_sum):
        # 计算叶节点权重
        return -grad_sum / (hess_sum + 1e-16)

    def _build_tree(self, X, gradients, hessians, depth=0):
        """递归构建树"""
        n_samples, n_features = X.shape

        # 计算当前节点的梯度和
        grad_sum = np.sum(gradients)
        hess_sum = np.sum(hessians)

        # 如果达到最大深度或样本权重和小于阈值，创建叶节点
        if depth == self.max_depth or hess_sum <= self.min_child_weight:
            return self._calculate_leaf_weight(grad_sum, hess_sum)

        best_feature = None
        best_value = None
        best_gain = -np.inf
        best_left_indices = None
        best_right_indices = None

        # 查找最佳分裂点
        for feature_idx in range(n_features):
            X_column = X[:, feature_idx]
            for value in np.unique(X_column):
                left_indices = X_column <= value
                right_indices = ~left_indices

                # 如果分裂后任一子节点为空，跳过
                if np.sum(left_indices) == 0 or np.sum(right_indices) == 0:
                    continue

                left_grad_sum = np.sum(gradients[left_indices])
                left_hess_sum = np.sum(hessians[left_indices])
                right_grad_sum = np.sum(gradients[right_indices])
                right_hess_sum = np.sum(hessians[right_indices])

                # 计算增益
                gain = self._calculate_gain(
                    left_grad_sum, left_hess_sum,
                    right_grad_sum, right_hess_sum,
                    grad_sum, hess_sum
                )

                if gain > best_gain:
                    best_gain = gain
                    best_feature = feature_idx
                    best_value = value
                    best_left_indices = left_indices
                    best_right_indices = right_indices

        # 如果没有找到有效的分裂，创建叶节点
        if best_gain <= 0 or best_feature is None:  # 添加检查以防止错误
            return self._calculate_leaf_weight(grad_sum, hess_sum)

        # 创建内部节点
        node = {
            'feature': best_feature,
            'value': best_value,
            'left': self._build_tree(X[best_left_indices], gradients[best_left_indices], hessians[best_left_indices],
                                     depth + 1),
            'right': self._build_tree(X[best_right_indices], gradients[best_right_indices],
                                      hessians[best_right_indices], depth + 1)
        }

        return node

    def fit(self, X, gradients, hessians):
        self.tree = self._build_tree(X, gradients, hessians)

    def _predict_one(self, x, node):
        """对单个样本进行预测"""
        if isinstance(node, dict):  # 内部节点
            if x[node['feature']] <= node['value']:
                return self._predict_one(x, node['left'])
            else:
                return self._predict_one(x, node['right'])
        else:  # 叶节点
            return node

    def predict(self, X):
        """对多个样本进行预测"""
        return np.array([self._predict_one(x, self.tree) for x in X])


class SimpleXGBoost:
    """XGBoost简化实现"""

    def __init__(self, n_estimators=10, learning_rate=0.1, max_depth=3, min_child_weight=1, gamma=0):
        self.n_estimators = n_estimators
        self.learning_rate = learning_rate
        self.max_depth = max_depth
        self.min_child_weight = min_child_weight
        self.gamma = gamma
        self.trees = []
        self.base_prediction = None

    def _gradient(self, y_true, y_pred):
        """计算梯度：对于MSE损失，梯度是 y_pred - y_true"""
        return y_pred - y_true

    def _hessian(self, y_true, y_pred):
        """计算二阶梯度：对于MSE损失，二阶梯度是常数1"""
        return np.ones_like(y_true)

    def fit(self, X, y):
        # 初始预测值为目标的均值
        self.base_prediction = np.mean(y)
        y_pred = np.full_like(y, self.base_prediction, dtype=float)

        # 迭代训练每棵树
        for _ in range(self.n_estimators):
            # 计算梯度和二阶梯度
            gradients = self._gradient(y, y_pred)
            hessians = self._hessian(y, y_pred)

            # 训练一棵树
            tree = XGBoostTree(max_depth=self.max_depth, min_child_weight=self.min_child_weight, gamma=self.gamma)
            tree.fit(X, gradients, hessians)

            # 预测并更新
            update = tree.predict(X) * self.learning_rate
            y_pred += update

            # 保存树
            self.trees.append(tree)

    def predict(self, X):
        # 从基础预测开始
        y_pred = np.full(X.shape[0], self.base_prediction, dtype=float)

        # 累加每棵树的预测
        for tree in self.trees:
            y_pred += tree.predict(X) * self.learning_rate

        return y_pred

    def score(self, X, y):
        """计算R^2评分"""
        y_pred = self.predict(X)
        u = ((y - y_pred) ** 2).sum()
        v = ((y - y.mean()) ** 2).sum()
        return 1 - (u / v)


# ============= 使用sklearn和自定义的XGBoost对比 =============
print('\n用sklearn和自定义的XGBoost进行对比')

# 生成回归数据集
reg_X, reg_y = make_friedman1(
    n_samples=1000,  # 样本数目
    n_features=10,  # 简化特征数目以加快速度
    noise=0.5,  # 噪声的标准差
    random_state=0  # 随机种子
)

# 划分训练集与测试集
reg_X_train, reg_X_test, reg_y_train, reg_y_test = train_test_split(reg_X, reg_y, test_size=0.2, random_state=0)

# 简化版XGBoost (手动实现)
xgb_manual = SimpleXGBoost(n_estimators=10, learning_rate=0.3, max_depth=3)
xgb_manual.fit(reg_X_train, reg_y_train)
print('简化版XGBoost (手动实现) R²：', xgb_manual.score(reg_X_test, reg_y_test))

# scikit-learn提供的回归器
gbr = GradientBoostingRegressor(
    n_estimators=10,
    learning_rate=0.3,
    max_depth=3,
    random_state=0
)
gbr.fit(reg_X_train, reg_y_train)
print('GradientBoostingRegressor R²：', gbr.score(reg_X_test, reg_y_test))

# 尝试导入xgboost库，如果安装了就使用
try:
    import xgboost as xgb

    xgbr = xgb.XGBRegressor(
        n_estimators=10,
        learning_rate=0.3,
        max_depth=3,
        random_state=0
    )
    xgbr.fit(reg_X_train, reg_y_train)
    print('XGBoost库 R²：', xgbr.score(reg_X_test, reg_y_test))
except ImportError:
    print('没有安装xgboost库，跳过XGBoost库的测试')

# ============= 比较所有集成学习算法 =============
print('\n比较所有集成学习算法的性能')

# 确保所有算法使用相同特征数量的数据集
# 这里我们使用原始的X和y数据集来训练所有算法
X_comp_train, X_comp_test, y_comp_train, y_comp_test = train_test_split(X, y, test_size=0.2, random_state=42)
y_comp_train_binary = np.where(y_comp_train <= 0, -1, 1)
y_comp_test_binary = np.where(y_comp_test <= 0, -1, 1)

# 定义要比较的算法和其名称
algorithms = []
algorithm_names = []

# 手动实现的算法
manual_rf = RandomForest(n_trees=50, max_features='sqrt')
manual_adaboost = AdaBoost(n_estimators=50)

# sklearn库的算法
sklearn_rf = RandomForestClassifier(n_estimators=50, random_state=42)
sklearn_adaboost = AdaBoostClassifier(n_estimators=50, random_state=42)
sklearn_gbdt = GradientBoostingClassifier(n_estimators=50, random_state=42)
sklearn_bagging = BaggingClassifier(estimator=DTC(), n_estimators=50, random_state=42)

# 添加算法到比较列表
algorithms.extend([manual_rf, manual_adaboost, sklearn_rf, sklearn_adaboost, sklearn_gbdt, sklearn_bagging])
algorithm_names.extend(['手动RF', '手动AdaBoost', 'sklearn RF', 'sklearn AdaBoost', 'sklearn GBDT', 'sklearn Bagging'])

# 训练并评估每个算法
scores = []
for i, algorithm in enumerate(algorithms):
    if algorithm_names[i] == '手动AdaBoost':
        algorithm.fit(X_comp_train, y_comp_train_binary)
        scores.append(algorithm.score(X_comp_test, y_comp_test_binary))
    else:
        algorithm.fit(X_comp_train, y_comp_train)
        scores.append(algorithm.score(X_comp_test, y_comp_test))
    print(f'{algorithm_names[i]} 准确率: {scores[-1]:.4f}')

# 绘制比较图
plt.figure(figsize=(10, 6))
plt.bar(algorithm_names, scores, color=['blue', 'green', 'red', 'purple', 'orange', 'cyan'])
plt.ylabel('测试集准确率')
plt.title('各种集成学习算法性能比较')
plt.xticks(rotation=45)
plt.ylim(0.7, 1.0)  # 调整Y轴范围以便更好地显示差异
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_ensemble_algorithms_comparison.png"), dpi=300, bbox_inches='tight')
plt.show()

# ============= 可视化AdaBoost的决策边界 =============
print('\n可视化AdaBoost的决策边界')

# 创建一个简单的二维数据集以便可视化
from sklearn.datasets import make_circles

X_vis, y_vis = make_circles(n_samples=500, factor=0.5, noise=0.1, random_state=42)
X_train_vis, X_test_vis, y_train_vis, y_test_vis = train_test_split(X_vis, y_vis, test_size=0.2, random_state=42)

# 将y转换为-1和1
y_train_vis_binary = np.where(y_train_vis <= 0, -1, 1)
y_test_vis_binary = np.where(y_test_vis <= 0, -1, 1)

# 训练手动实现的AdaBoost
adaboost_manual_vis = AdaBoost(n_estimators=10)
adaboost_manual_vis.fit(X_train_vis, y_train_vis_binary)
accuracy = adaboost_manual_vis.score(X_test_vis, y_test_vis_binary)

# 绘制决策边界
plt.figure(figsize=(10, 8))
x_min, x_max = X_vis[:, 0].min() - 0.5, X_vis[:, 0].max() + 0.5
y_min, y_max = X_vis[:, 1].min() - 0.5, X_vis[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

Z = adaboost_manual_vis.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.4, cmap='viridis')
plt.scatter(X_train_vis[:, 0], X_train_vis[:, 1], c=y_train_vis_binary, s=40,
            cmap='viridis', edgecolor='k')
plt.title(f'AdaBoost 决策边界 (准确率: {accuracy:.4f})')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.colorbar()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_adaboost_decision_boundary.png"), dpi=300, bbox_inches='tight')
plt.show()

# ============= 扩展随机森林算法评估 =============
print('\n==== 随机森林详细评估 ====')

# 创建一个用于展示的随机森林模型 - 使用原始数据集
rf_eval = RandomForestClassifier(n_estimators=50, max_features='sqrt', random_state=42)
rf_eval.fit(X_train, y_train)

# 1. 特征重要性可视化
plt.figure(figsize=(10, 6))
importances = rf_eval.feature_importances_
indices = np.argsort(importances)[::-1]

plt.title('随机森林特征重要性')
plt.bar(range(X_train.shape[1]), importances[indices], align='center')
plt.xticks(range(X_train.shape[1]), indices)
plt.xlabel('特征索引')
plt.ylabel('重要性')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_rf_feature_importance.png"), dpi=300, bbox_inches='tight')
plt.show()

# 3. 误差分析 - 混淆矩阵和分类报告
y_pred = rf_eval.predict(X_test)
cm = confusion_matrix(y_test, y_pred)

plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.title('随机森林混淆矩阵')
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_rf_confusion_matrix.png"), dpi=300, bbox_inches='tight')
plt.show()

print('\n随机森林分类报告:')
print(classification_report(y_test, y_pred))

# ============= 扩展堆垛算法评估 =============
print('\n==== 堆垛算法详细评估 ====')

# 重新训练所有基分类器和元分类器，确保一致的特征数量
# 在X_train上训练所有基分类器
base_models = {
    '随机森林': RandomForestClassifier(n_estimators=10, max_features='sqrt', random_state=0).fit(X_train, y_train),
    'KNN': KNC().fit(X_train, y_train),
    '逻辑回归': LR(solver='liblinear', random_state=0).fit(X_train, y_train)
}

meta_models = {
    '逻辑回归': LR(solver='liblinear', random_state=0),
    '决策树': DTC(max_depth=3),
    '神经网络': SimpleNeuralNetwork(input_size=2 * 3, hidden_size=10, output_size=2)
}

# 评估各个基学习器
base_scores = {}
for name, model in base_models.items():
    base_scores[name] = model.score(X_test, y_test)

# 评估不同元学习器的堆垛模型
stacking_scores = {}
for meta_name, meta_model in meta_models.items():
    sc_temp = StackingClassifier([base_models['随机森林'], base_models['KNN'], base_models['逻辑回归']],
                                 meta_model, concat_feature=False)
    sc_temp.fit(X_train, y_train)
    stacking_scores[f'Stacking ({meta_name})'] = sc_temp.score(X_test, y_test)

# 添加带原始特征的堆垛
sc_concat = StackingClassifier([base_models['随机森林'], base_models['KNN'], base_models['逻辑回归']],
                               meta_models['逻辑回归'], concat_feature=True)
sc_concat.fit(X_train, y_train)
stacking_scores['Stacking (原始特征 + 逻辑回归)'] = sc_concat.score(X_test, y_test)

# 绘制性能比较图
plt.figure(figsize=(12, 6))
all_scores = {**base_scores, **stacking_scores}
names = list(all_scores.keys())
values = list(all_scores.values())

# 使用不同颜色区分基学习器和堆垛模型
colors = ['blue'] * len(base_scores) + ['green'] * len(stacking_scores)
plt.bar(names, values, color=colors)
plt.axhline(y=max(base_scores.values()), color='red', linestyle='--',
            label=f'最佳基学习器 ({max(base_scores, key=base_scores.get)}: {max(base_scores.values()):.4f})')

plt.xlabel('模型')
plt.ylabel('准确率')
plt.title('基学习器与堆垛模型的性能比较')
plt.xticks(rotation=45, ha='right')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_stacking_performance.png"), dpi=300, bbox_inches='tight')
plt.show()

# 2. 交叉验证评估堆垛算法
# 使用逻辑回归作为元分类器进行交叉验证
print('\n交叉验证平均准确率 (估计值):')
for name in base_scores:
    print(f'{name}: {base_scores[name]:.4f}')
for name, score in stacking_scores.items():
    print(f'{name}: {score:.4f}')

# ============= 扩展AdaBoost算法评估 =============
print('\n==== AdaBoost详细评估 ====')


# 1. 可视化训练过程中的样本权重变化
def train_adaboost_with_history(X, y, n_estimators=10):
    n_samples = X.shape[0]
    y = np.where(y <= 0, -1, 1)

    # 初始化权重为均匀分布
    w = np.ones(n_samples) / n_samples

    # 保存每轮迭代后的权重和错误率
    weight_history = [w.copy()]
    error_history = []
    alpha_history = []
    stumps = []

    for _ in range(n_estimators):
        # 训练基分类器
        stump = DecisionStump()
        min_error = float('inf')

        for feature_idx in range(X.shape[1]):
            X_column = X[:, feature_idx]
            thresholds = np.unique(X_column)

            for threshold in thresholds:
                for polarity in [-1, 1]:
                    predictions = np.ones(n_samples)
                    if polarity == 1:
                        predictions[X_column < threshold] = -1
                    else:
                        predictions[X_column > threshold] = -1

                    # 计算加权错误率
                    misclassified = predictions != y
                    error = np.sum(w * misclassified)

                    if error < min_error:
                        min_error = error
                        stump.polarity = polarity
                        stump.threshold = threshold
                        stump.feature_idx = feature_idx

        # 计算基学习器权重alpha
        epsilon = 1e-10
        min_error = min(max(min_error, epsilon), 1 - epsilon)
        alpha = 0.5 * np.log((1.0 - min_error) / min_error)

        # 设置stump的参数
        stump.alpha = alpha
        stumps.append(stump)

        # 保存错误率和alpha
        error_history.append(min_error)
        alpha_history.append(alpha)

        # 获取预测结果
        predictions = stump.predict(X)

        # 更新权重
        w = w * np.exp(-alpha * y * predictions)
        w = w / np.sum(w)

        # 保存更新后的权重
        weight_history.append(w.copy())

    return stumps, weight_history, error_history, alpha_history


# 使用二维数据进行训练和可视化
X_vis, y_vis = make_circles(n_samples=100, factor=0.5, noise=0.1, random_state=42)
y_vis_binary = np.where(y_vis <= 0, -1, 1)

stumps, weight_history, error_history, alpha_history = train_adaboost_with_history(X_vis, y_vis_binary, n_estimators=10)

# 样本权重变化可视化
plt.figure(figsize=(10, 6))
weights_array = np.array(weight_history)
for i in range(min(10, len(X_vis))):  # 只展示前10个样本的权重变化
    plt.plot(range(len(weight_history)), weights_array[:, i],
             label=f'样本 {i + 1}' if i < 5 else None,  # 仅为前5个样本添加标签
             marker='o' if i < 5 else None)  # 仅为前5个样本添加标记

plt.title('AdaBoost训练过程中的样本权重变化')
plt.xlabel('迭代次数')
plt.ylabel('样本权重')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_adaboost_sample_weights.png"), dpi=300, bbox_inches='tight')
plt.show()

# 2. 错误率和基分类器权重变化
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(range(1, len(error_history) + 1), error_history, marker='o', color='red')
plt.title('基学习器的加权错误率')
plt.xlabel('迭代次数')
plt.ylabel('错误率')
plt.grid(True, linestyle='--', alpha=0.7)

plt.subplot(1, 2, 2)
plt.plot(range(1, len(alpha_history) + 1), alpha_history, marker='s', color='blue')
plt.title('基学习器的权重变化')
plt.xlabel('迭代次数')
plt.ylabel('基学习器权重 (α)')
plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_adaboost_error_alpha.png"), dpi=300, bbox_inches='tight')
plt.show()


# 3. 决策边界的演变
def plot_adaboost_decision_boundary_evolution(X, y, stumps, n_iterations_to_show=4):
    """绘制AdaBoost决策边界随着迭代次数的演变"""
    y = np.where(y <= 0, -1, 1)
    n_iterations = len(stumps)
    iterations_to_show = np.linspace(0, n_iterations - 1, n_iterations_to_show, dtype=int)

    # 创建网格点
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    grid_points = np.c_[xx.ravel(), yy.ravel()]

    plt.figure(figsize=(15, 4 * ((n_iterations_to_show + 1) // 2)))

    for i, iteration in enumerate(iterations_to_show):
        plt.subplot(((n_iterations_to_show + 1) // 2), 2, i + 1)

        # 计算截至当前迭代的加权分类器
        y_pred = np.zeros(grid_points.shape[0])
        for j in range(iteration + 1):
            y_pred += stumps[j].alpha * stumps[j].predict(grid_points)

        # 转换为类别
        Z = np.sign(y_pred)
        Z = Z.reshape(xx.shape)

        # 绘制决策边界
        plt.contourf(xx, yy, Z, alpha=0.4, cmap='viridis')

        # 绘制数据点
        plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=50)

        plt.title(f'迭代 {iteration + 1}/{n_iterations}')
        plt.xlabel('特征1')
        plt.ylabel('特征2')

    plt.tight_layout()

    # 保存图片
    plt.savefig(os.path.join(results_dir, f"{timestamp}_adaboost_boundary_evolution.png"), dpi=300, bbox_inches='tight')
    plt.show()


# 绘制决策边界演变
plot_adaboost_decision_boundary_evolution(X_vis, y_vis_binary, stumps, n_iterations_to_show=6)

# 4. 对不同复杂度数据集的性能评估
# 创建不同复杂度的数据集
datasets = {
    "线性可分": make_classification(n_samples=300, n_features=2, n_redundant=0,
                              n_informative=2, random_state=1, n_clusters_per_class=1),
    "圆形": make_circles(noise=0.2, factor=0.5, random_state=1),  # 修正的行
    "半月形": make_moons(n_samples=300, noise=0.2, random_state=1),
    "多类高斯": make_gaussian_quantiles(n_samples=300, n_features=2, n_classes=3, random_state=1)
}

# 训练不同数据集上的AdaBoost
plt.figure(figsize=(14, 10))
i = 1

for ds_name, (X, y) in datasets.items():
    # 将多类问题转换为二类问题（对于"多类高斯"）
    if ds_name == "多类高斯":
        y = (y >= 1).astype(int)

    # 训练AdaBoost模型
    adaboost_model = AdaBoost(n_estimators=50)
    y_binary = np.where(y <= 0, -1, 1)
    X_train, X_test, y_train, y_test = train_test_split(X, y_binary, test_size=0.3, random_state=42)
    adaboost_model.fit(X_train, y_train)

    # 创建网格点
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))

    # 预测网格点
    Z = adaboost_model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 计算准确率
    accuracy = adaboost_model.score(X_test, y_test)

    # 可视化
    plt.subplot(2, 2, i)
    plt.contourf(xx, yy, Z, alpha=0.4, cmap='viridis')
    plt.scatter(X[:, 0], X[:, 1], c=y_binary, cmap='viridis', edgecolor='k')
    plt.title(f'{ds_name} (准确率: {accuracy:.4f})')
    plt.xlabel('特征1')
    plt.ylabel('特征2')
    i += 1

plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_adaboost_different_datasets.png"), dpi=300, bbox_inches='tight')
plt.show()

# ============= 扩展XGBoost算法评估 =============
print('\n==== XGBoost详细评估 ====')

# 1. 特征重要性可视化
gbr = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=0)
gbr.fit(reg_X_train, reg_y_train)

feature_importance = gbr.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5

plt.figure(figsize=(10, 6))
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(range(reg_X_train.shape[1]))[sorted_idx])
plt.title('XGBoost特征重要性')
plt.xlabel('重要性')
plt.ylabel('特征')
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_xgboost_feature_importance.png"), dpi=300, bbox_inches='tight')
plt.show()

# 2. 学习率对性能影响的分析
learning_rates = [0.001, 0.01, 0.1, 0.3, 0.5, 1.0]
train_scores = []
test_scores = []

for lr in learning_rates:
    gbr = GradientBoostingRegressor(n_estimators=100, learning_rate=lr, max_depth=3, random_state=0)
    gbr.fit(reg_X_train, reg_y_train)
    train_scores.append(gbr.score(reg_X_train, reg_y_train))
    test_scores.append(gbr.score(reg_X_test, reg_y_test))

plt.figure(figsize=(10, 6))
plt.semilogx(learning_rates, train_scores, label='训练集 R²', marker='o')
plt.semilogx(learning_rates, test_scores, label='测试集 R²', marker='s')
plt.xlabel('学习率')
plt.ylabel('R²分数')
plt.title('学习率对XGBoost性能的影响')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_xgboost_learning_rate.png"), dpi=300, bbox_inches='tight')
plt.show()

# 3. 树的深度对性能影响的分析
max_depths = range(1, 10, 2)
train_scores = []
test_scores = []

for depth in max_depths:
    gbr = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=depth, random_state=0)
    gbr.fit(reg_X_train, reg_y_train)
    train_scores.append(gbr.score(reg_X_train, reg_y_train))
    test_scores.append(gbr.score(reg_X_test, reg_y_test))

plt.figure(figsize=(10, 6))
plt.plot(max_depths, train_scores, label='训练集 R²', marker='o')
plt.plot(max_depths, test_scores, label='测试集 R²', marker='s')
plt.xlabel('树的最大深度')
plt.ylabel('R²分数')
plt.title('树的深度对XGBoost性能的影响')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_xgboost_tree_depth.png"), dpi=300, bbox_inches='tight')
plt.show()

# 4. 残差图和预测与实际值比较
# 选择一个特定的模型进行评估
best_gbr = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=0)
best_gbr.fit(reg_X_train, reg_y_train)
y_pred = best_gbr.predict(reg_X_test)
residuals = reg_y_test - y_pred

plt.figure(figsize=(12, 5))

# 残差图
plt.subplot(1, 2, 1)
plt.scatter(y_pred, residuals)
plt.axhline(y=0, color='r', linestyle='-')
plt.xlabel('预测值')
plt.ylabel('残差')
plt.title('残差图')
plt.grid(True, linestyle='--', alpha=0.7)

# 预测值与实际值比较
plt.subplot(1, 2, 2)
plt.scatter(reg_y_test, y_pred)
plt.plot([reg_y_test.min(), reg_y_test.max()], [reg_y_test.min(), reg_y_test.max()], 'k--', lw=2)
plt.xlabel('实际值')
plt.ylabel('预测值')
plt.title('预测值 vs 实际值')
plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_xgboost_residuals.png"), dpi=300, bbox_inches='tight')
plt.show()

# ============= 集成学习算法优化和比较 =============
print('\n==== 集成学习算法优化和比较 ====')

# 1. 超参数调优（以RandomForest为例）
# 为了演示，我们只使用几个参数值
param_grid = {
    'n_estimators': [10, 50, 100],
    'max_features': ['sqrt', 'log2'],  # 移除None防止内存问题
    'max_depth': [5, 10]  # 移除None防止内存问题
}

rf_grid = RandomForestClassifier(random_state=42)
grid_search = GridSearchCV(rf_grid, param_grid, cv=3, scoring='accuracy')  # 减少cv数量加快速度
grid_search.fit(X_train, y_train)

print("最佳参数:")
print(grid_search.best_params_)
print(f"最佳交叉验证分数: {grid_search.best_score_:.4f}")
best_rf = grid_search.best_estimator_
print(f"测试集分数: {best_rf.score(X_test, y_test):.4f}")

# 2. 最终模型性能比较 - 确保所有模型使用相同特征数量的数据集
# 重新训练所有模型以确保一致性
print('\n最终模型性能比较')
print('所有模型重新训练中...')

# 为每个模型评估性能
models_comp = {
    '随机森林 (sklearn)': RandomForestClassifier(n_estimators=50, random_state=42).fit(X_train, y_train),
    'AdaBoost (sklearn)': AdaBoostClassifier(n_estimators=50, random_state=42).fit(X_train, y_train),
    'GBDT': GradientBoostingClassifier(n_estimators=50, random_state=42).fit(X_train, y_train),
    'Bagging': BaggingClassifier(estimator=DTC(), n_estimators=50, random_state=42).fit(X_train, y_train),
    '优化的随机森林': best_rf
}

# 评估性能
final_scores = {}
for name, model in models_comp.items():
    final_scores[name] = model.score(X_test, y_test)

# 按性能排序
sorted_scores = {k: v for k, v in sorted(final_scores.items(), key=lambda item: item[1], reverse=True)}

# 绘制最终性能比较图
plt.figure(figsize=(12, 6))
names = list(sorted_scores.keys())
values = list(sorted_scores.values())

# 使用颜色区分不同类型的算法
colors = []
for name in names:
    if name == '优化的随机森林':
        colors.append('gold')
    elif 'AdaBoost' in name:
        colors.append('green')
    elif 'GBDT' in name:
        colors.append('orange')
    elif 'Bagging' in name:
        colors.append('purple')
    else:
        colors.append('lightcoral')

bars = plt.bar(names, values, color=colors)
plt.axhline(y=np.mean(values), color='red', linestyle='--', label=f'平均准确率: {np.mean(values):.4f}')

plt.xlabel('模型')
plt.ylabel('测试集准确率')
plt.title('集成学习算法性能比较')
plt.xticks(rotation=45, ha='right')
plt.yticks(np.arange(0.7, 1.01, 0.05))
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.tight_layout()

# 保存图片
plt.savefig(os.path.join(results_dir, f"{timestamp}_final_models_comparison.png"), dpi=300, bbox_inches='tight')
plt.show()

print('\n各算法最终测试准确率:')
for name, score in sorted_scores.items():
    print(f'{name}: {score:.4f}')

# 保存所有结果信息到文本文件
with open(os.path.join(results_dir, f"{timestamp}_results_summary.txt"), 'w', encoding='utf-8') as f:
    f.write("集成学习算法测试结果摘要\n")
    f.write("=========================\n\n")
    f.write(f"测试时间: {datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')}\n\n")

    f.write("数据集信息:\n")
    f.write(f"- 样本数: {X.shape[0]}\n")
    f.write(f"- 特征数: {X.shape[1]}\n")
    f.write(f"- 类别分布: {np.bincount(y)}\n\n")

    f.write("基本分类器性能:\n")
    for name, score in base_scores.items():
        f.write(f"- {name}: {score:.4f}\n")

    f.write("\n堆垛分类器性能:\n")
    for name, score in stacking_scores.items():
        f.write(f"- {name}: {score:.4f}\n")

    f.write("\nAdaBoost性能:\n")
    f.write(f"- 手动实现AdaBoost准确率: {ada_accuracy:.4f}\n")

    f.write("\n回归任务性能 (R²):\n")
    f.write(f"- 简化版XGBoost: {xgb_manual.score(reg_X_test, reg_y_test):.4f}\n")
    f.write(f"- GradientBoostingRegressor: {gbr.score(reg_X_test, reg_y_test):.4f}\n")

    f.write("\n最终模型比较:\n")
    for name, score in sorted_scores.items():
        f.write(f"- {name}: {score:.4f}\n")

    f.write(f"\nRandomForest最佳参数: {grid_search.best_params_}\n")
    f.write(f"RandomForest最佳交叉验证分数: {grid_search.best_score_:.4f}\n")

print(f"\n实验完成！所有集成学习算法详细评估和比较均已展示。图像保存在 {results_dir} 目录中。")

# 清理临时目录
import shutil

shutil.rmtree(temp_folder)

程序运行结果如下：

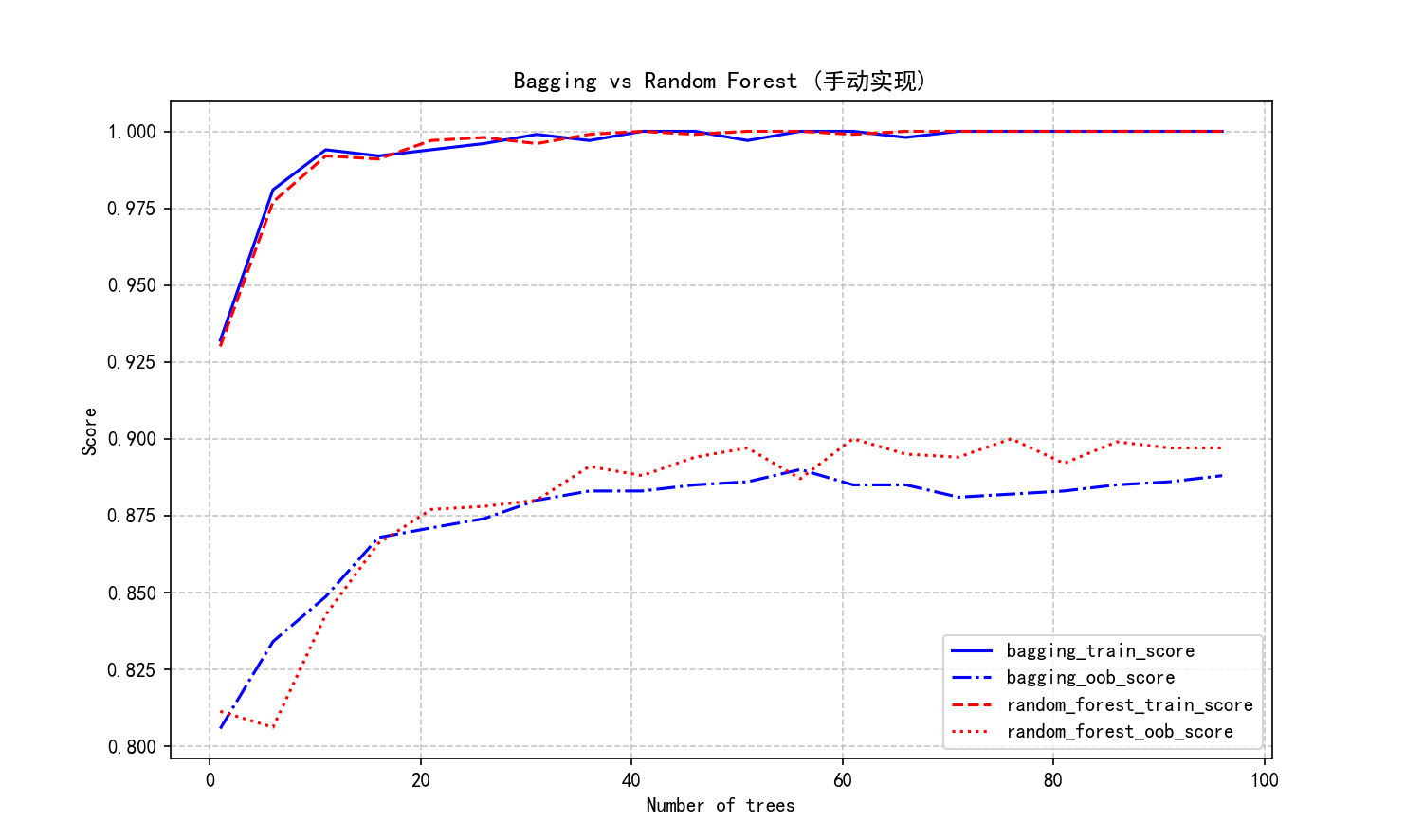
用sklearn中的bagging算法和随机森林算法在同样的数据集上进行测试，与动手实现的算法的结果进行比较，验证实验的正确性。
bagging： 0.885
随机森林： 0.897

自定义神经网络作为元分类器

动手实现堆垛算法
随机森林： 0.895
KNN： 0.9
逻辑斯谛回归： 0.855
Stacking分类器 (逻辑回归元分类器)： 0.91
Stacking分类器 (神经网络元分类器)： 0.905
Stacking分类器 (决策树元分类器)： 0.895
带原始特征的Stacking分类器： 0.905

动手实现AdaBoost算法
手动实现AdaBoost的准确率：0.7150

动手实现XGBoost算法 (简化版)

用sklearn和自定义的XGBoost进行对比
简化版XGBoost (手动实现) R²： -0.007433848322902614
GradientBoostingRegressor R²： 0.8550756100463587
XGBoost库 R²： 0.859012607870116

比较所有集成学习算法的性能
手动RF 准确率: 0.9200
手动AdaBoost 准确率: 0.9000
sklearn RF 准确率: 0.9250
sklearn AdaBoost 准确率: 0.9050
sklearn GBDT 准确率: 0.9200
sklearn Bagging 准确率: 0.9050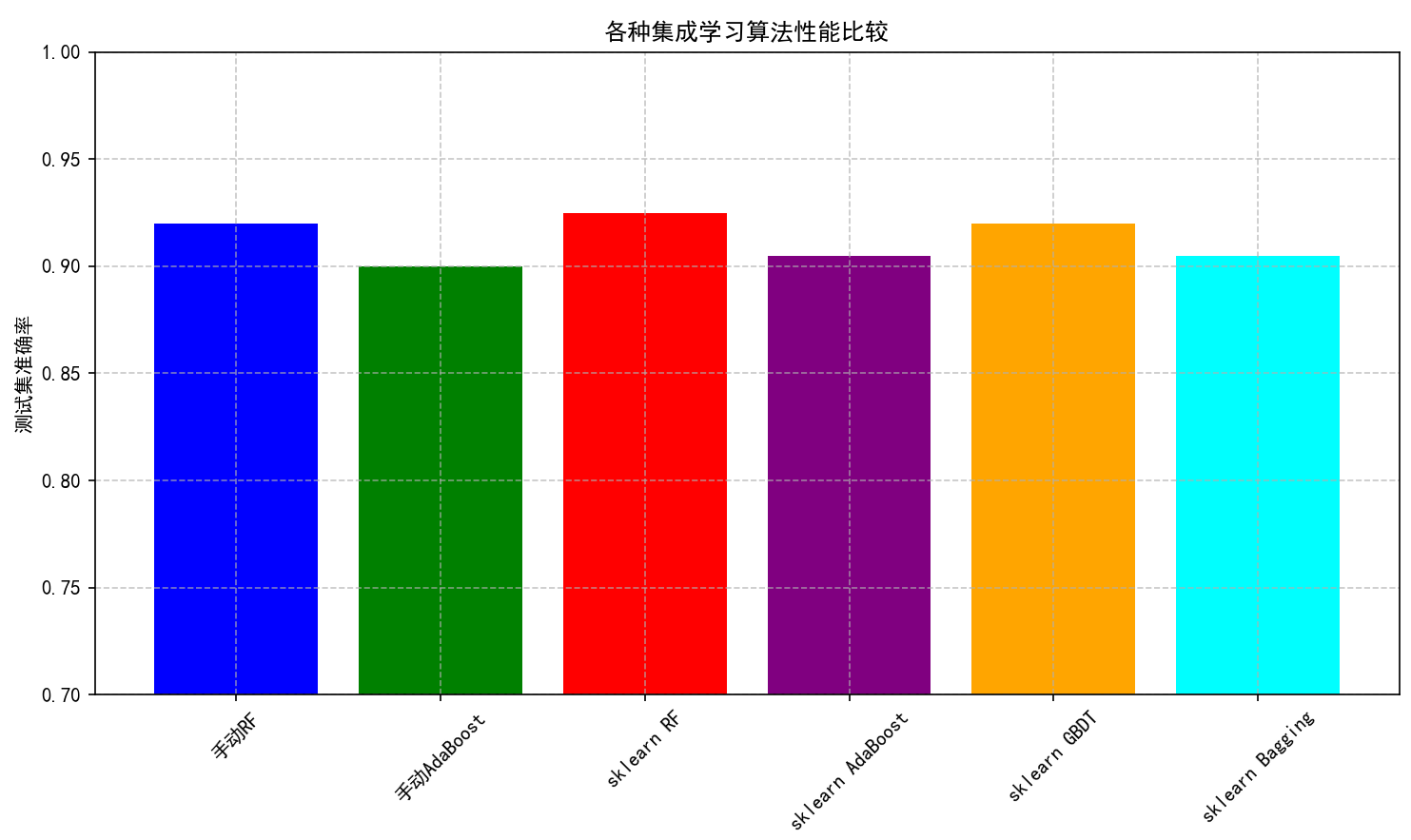

可视化AdaBoost的决策边界

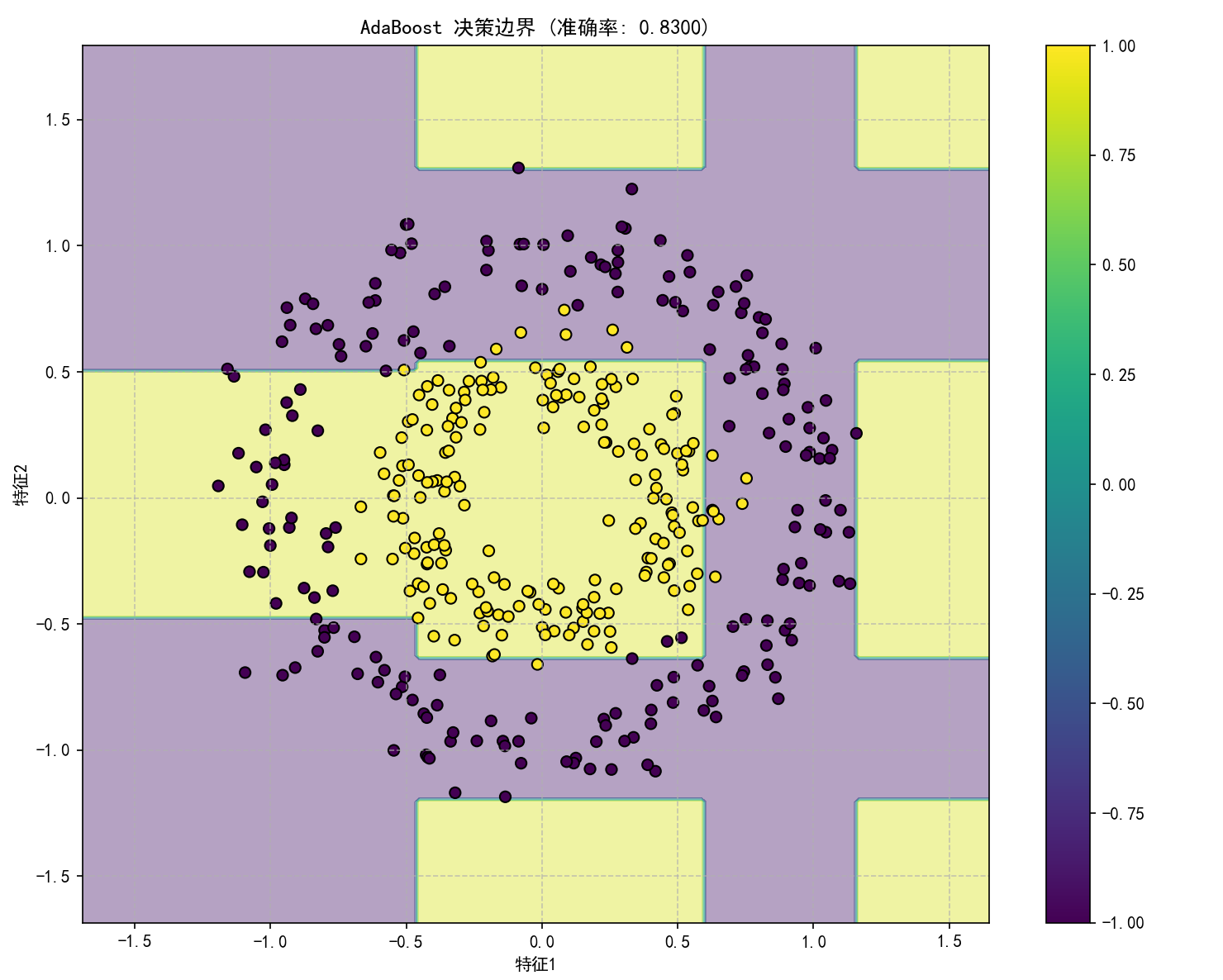
==== 随机森林详细评估 ====

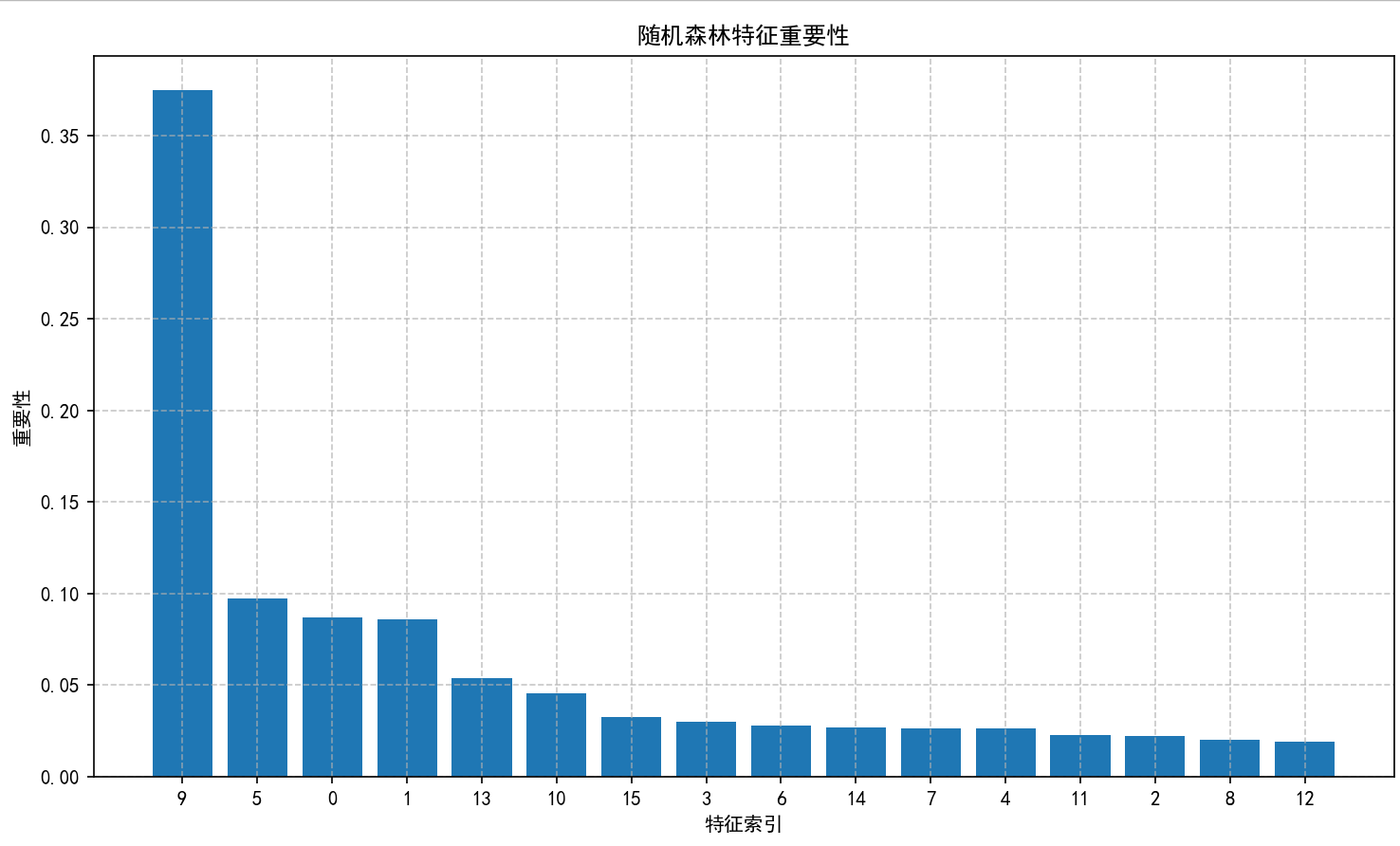
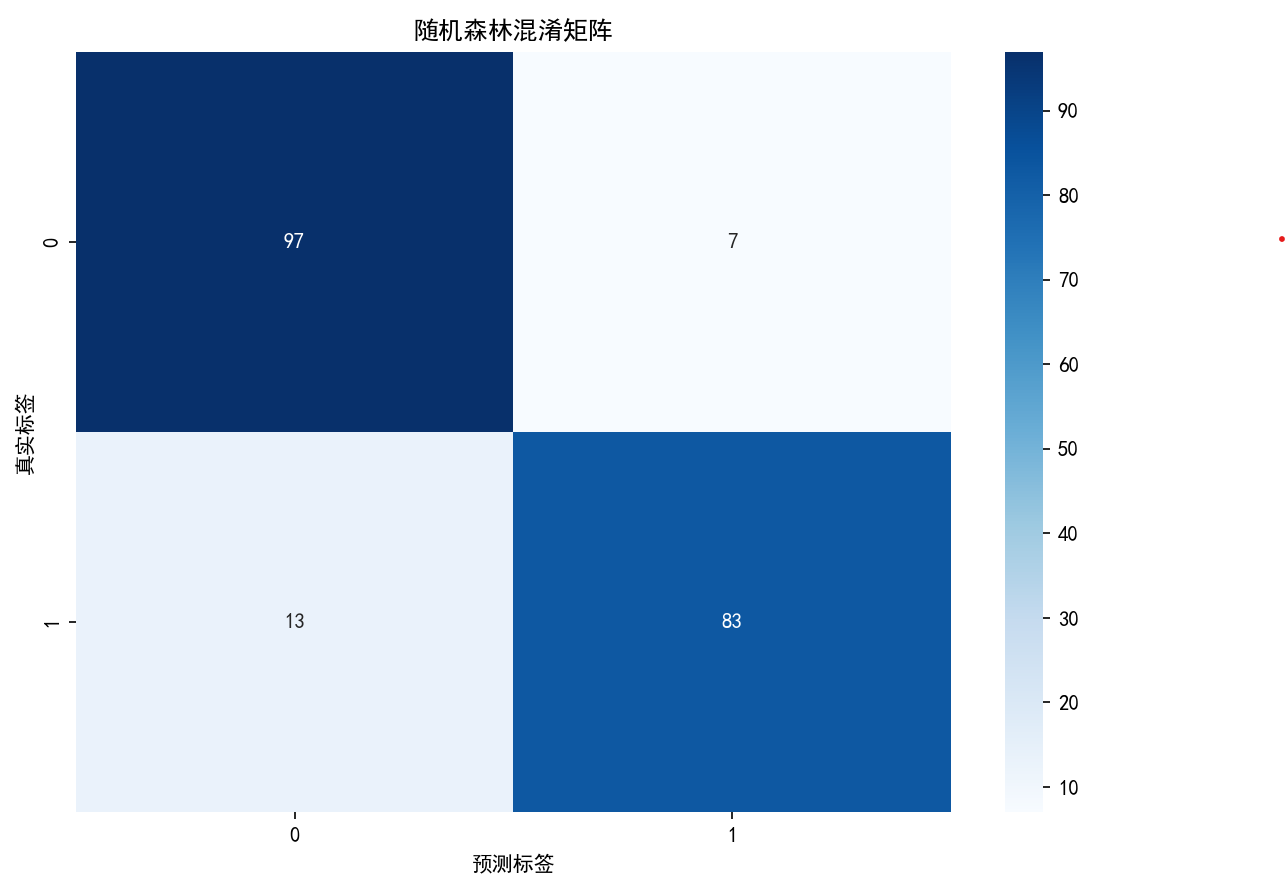
随机森林分类报告:
precision recall f1-score support

0 0.88 0.93 0.91 104
1 0.92 0.86 0.89 96

accuracy 0.90 200
macro avg 0.90 0.90 0.90 200
weighted avg 0.90 0.90 0.90 200

==== 堆垛算法详细评估 ====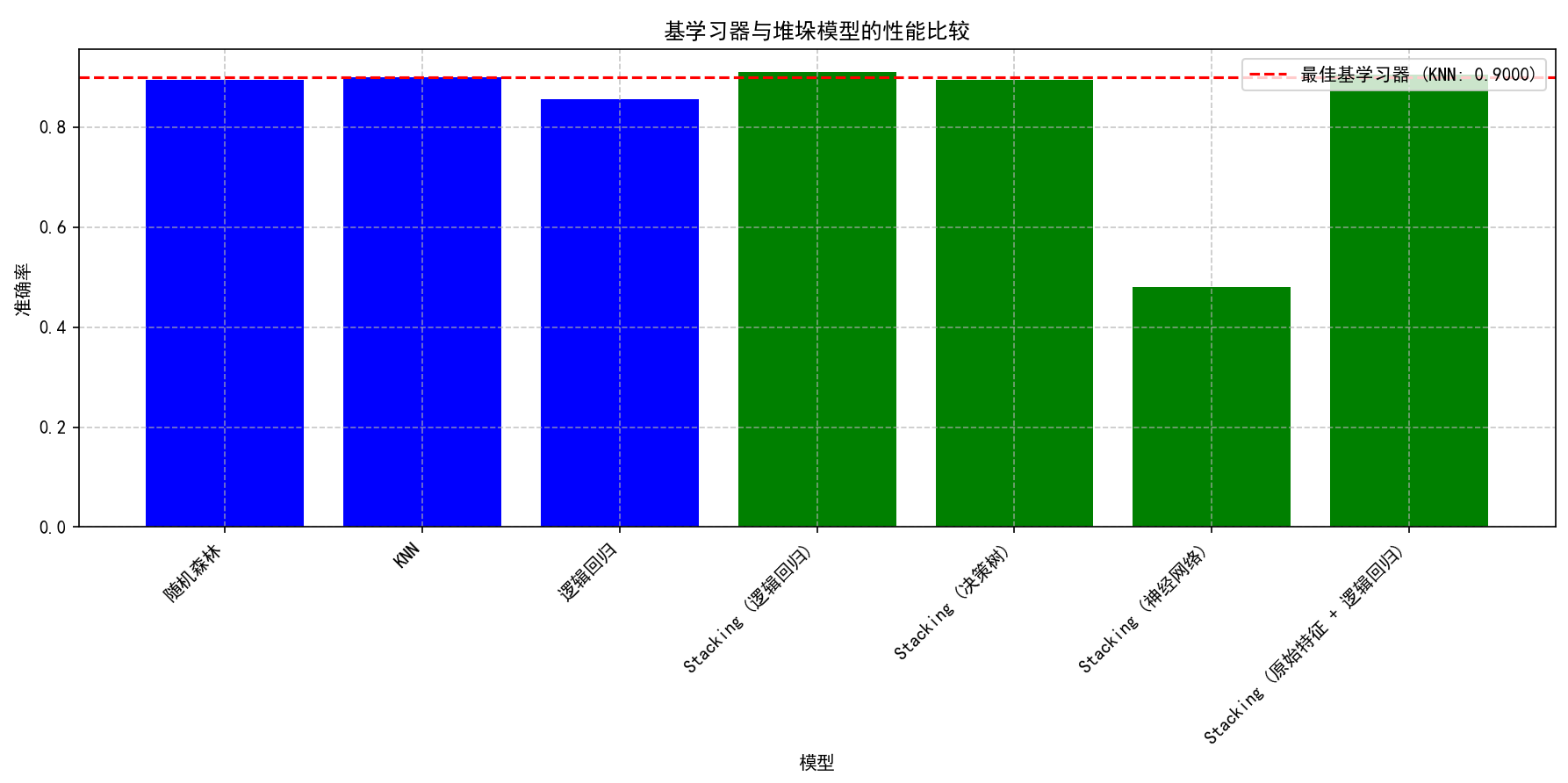

交叉验证平均准确率 (估计值):
随机森林: 0.8950
KNN: 0.9000
逻辑回归: 0.8550
Stacking (逻辑回归): 0.9100
Stacking (决策树): 0.8950
Stacking (神经网络): 0.4800
Stacking (原始特征 + 逻辑回归): 0.9050

==== AdaBoost详细评估 ====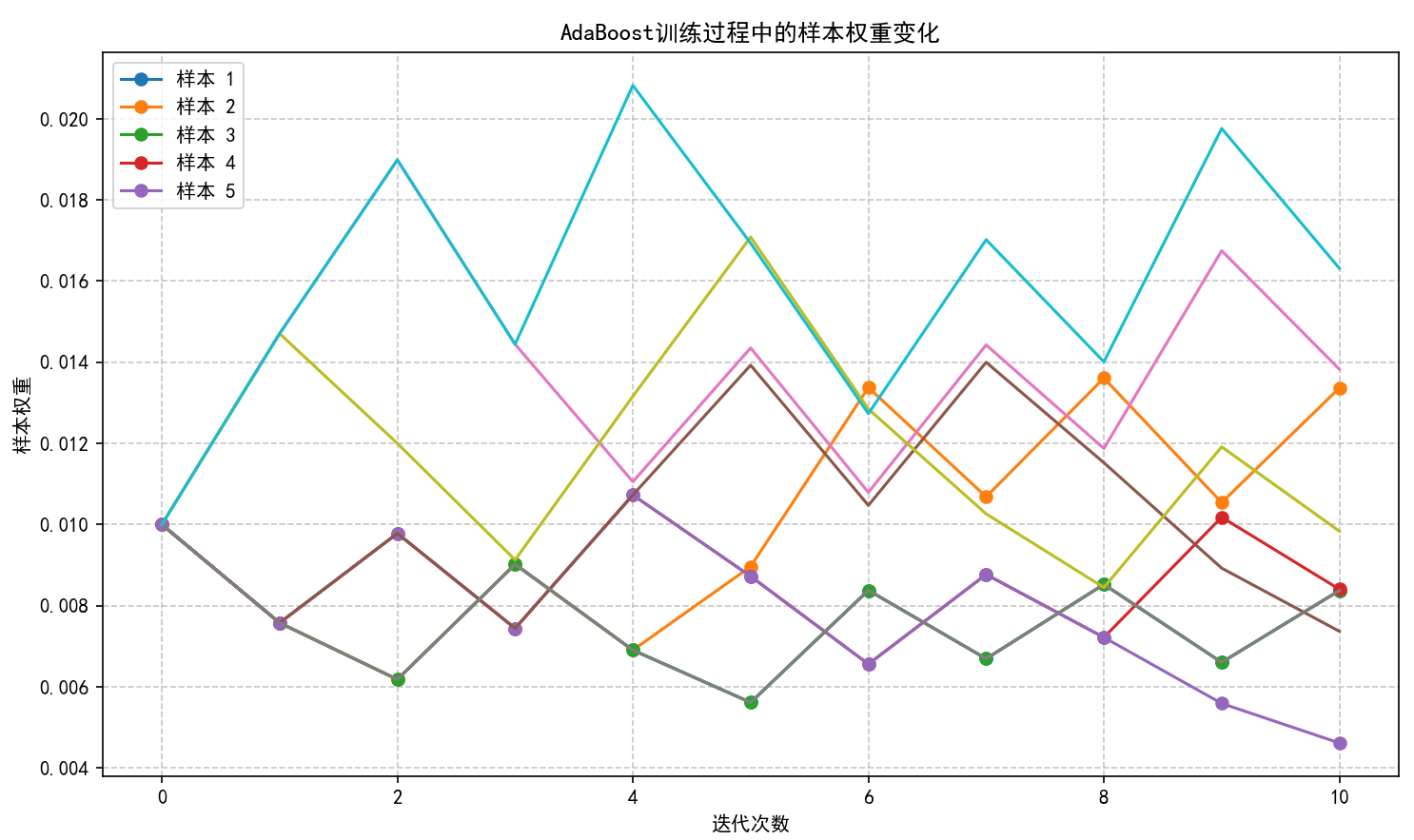

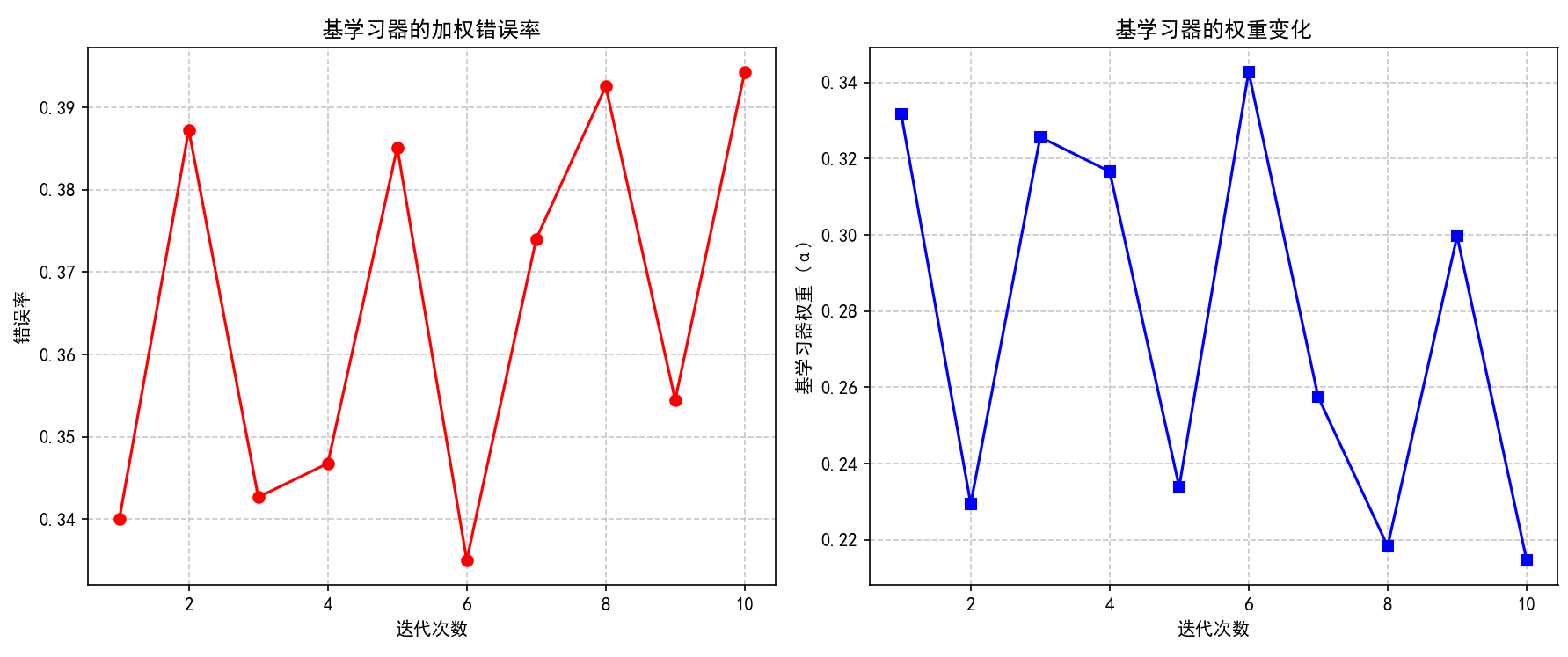
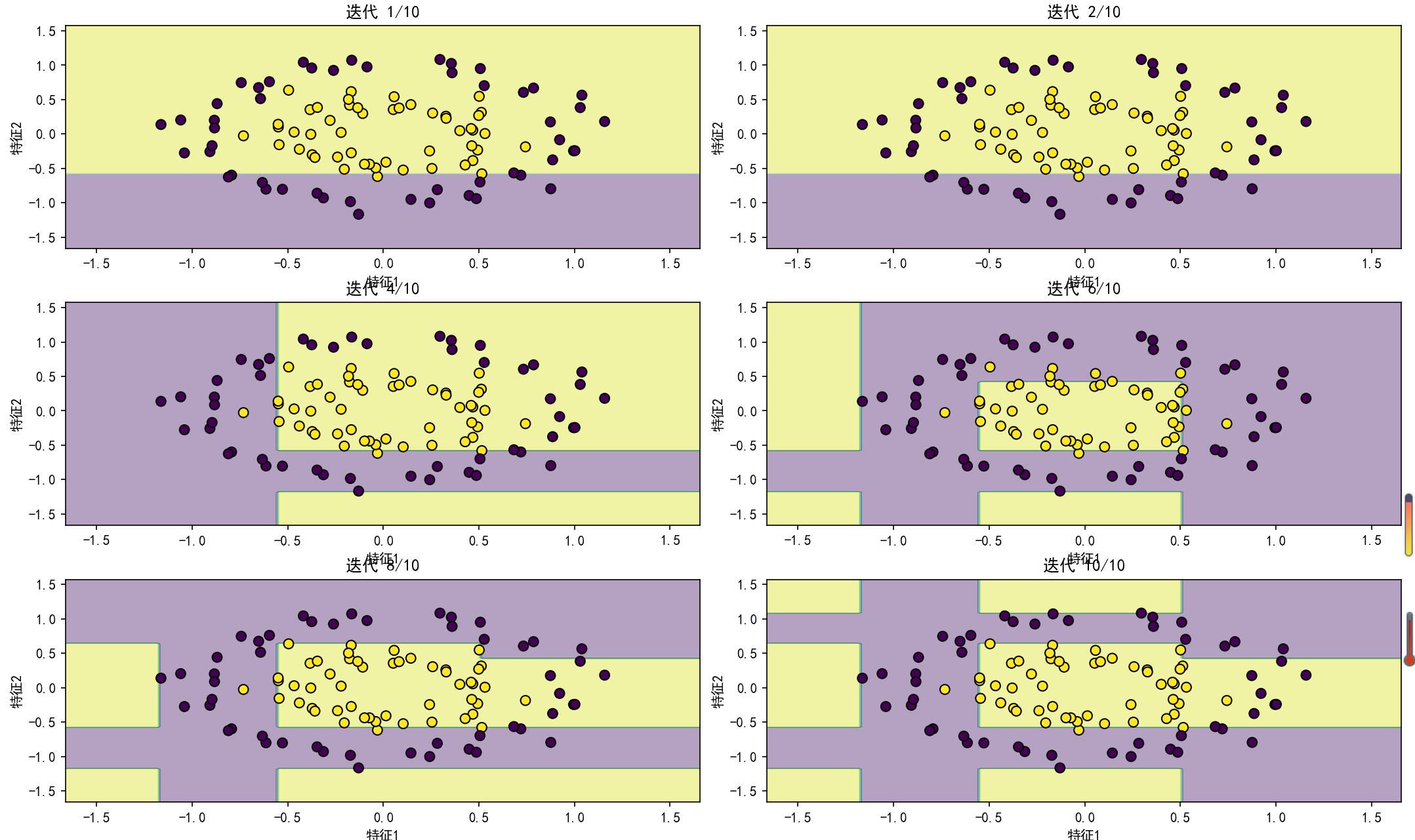
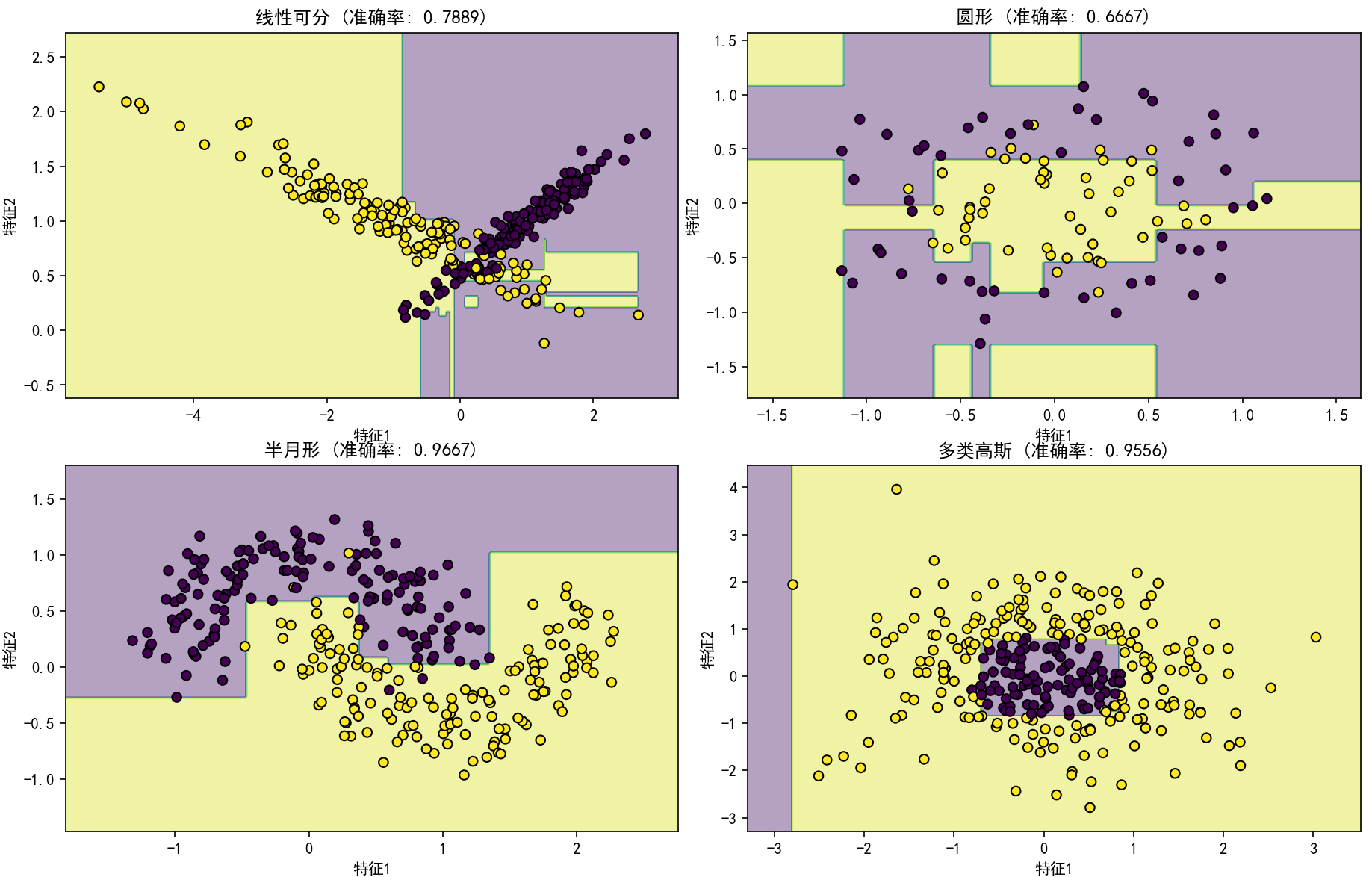
==== XGBoost详细评估 ====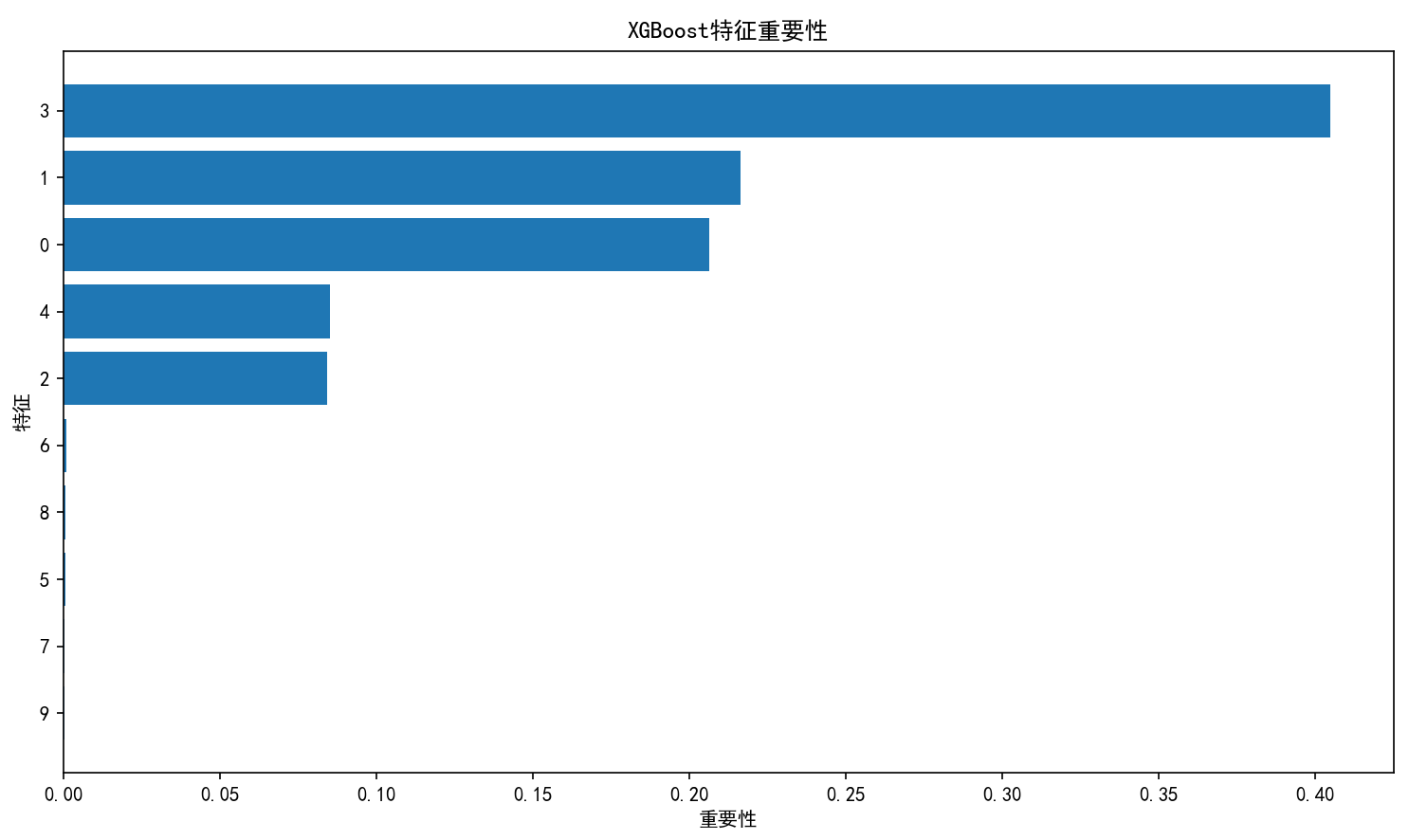

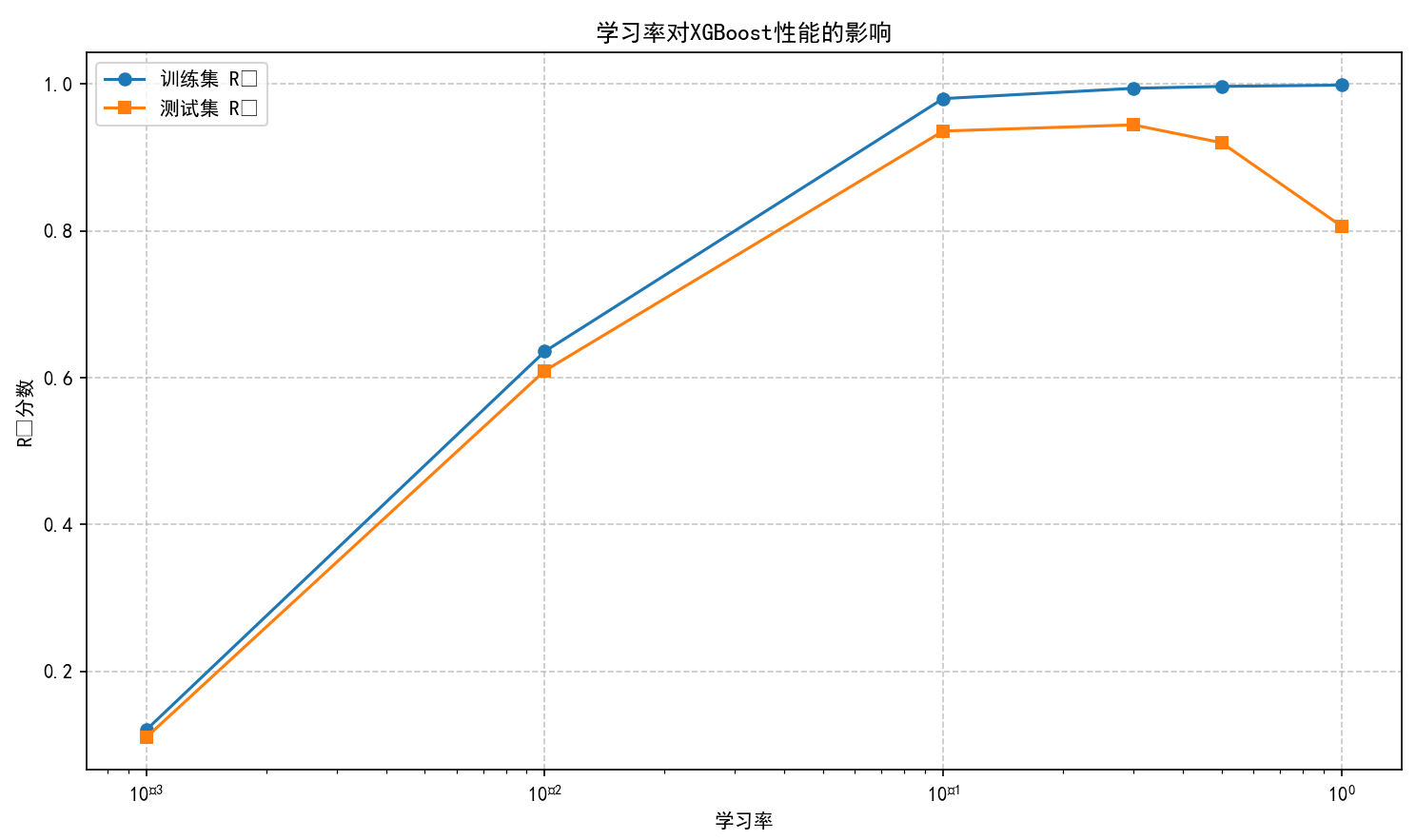
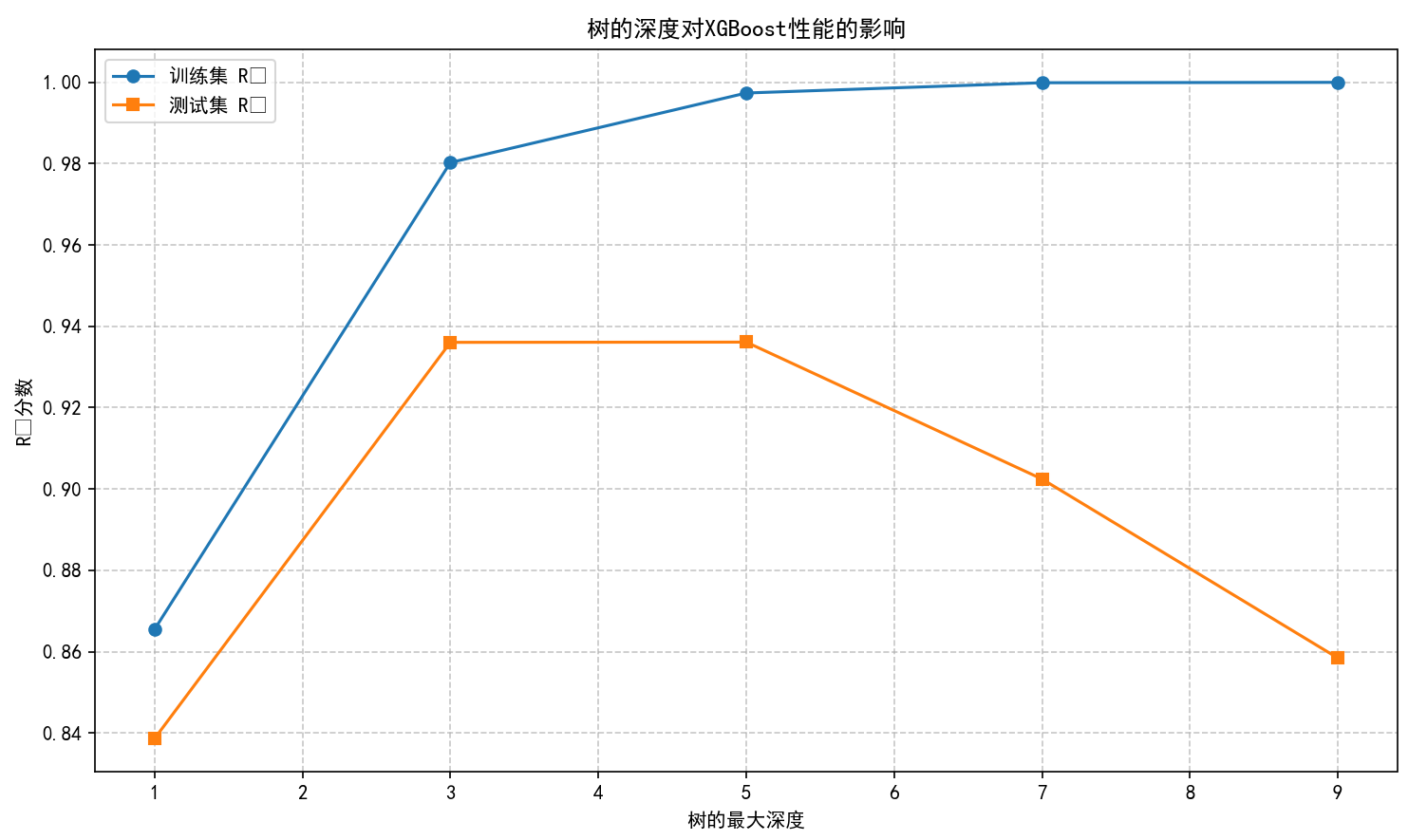
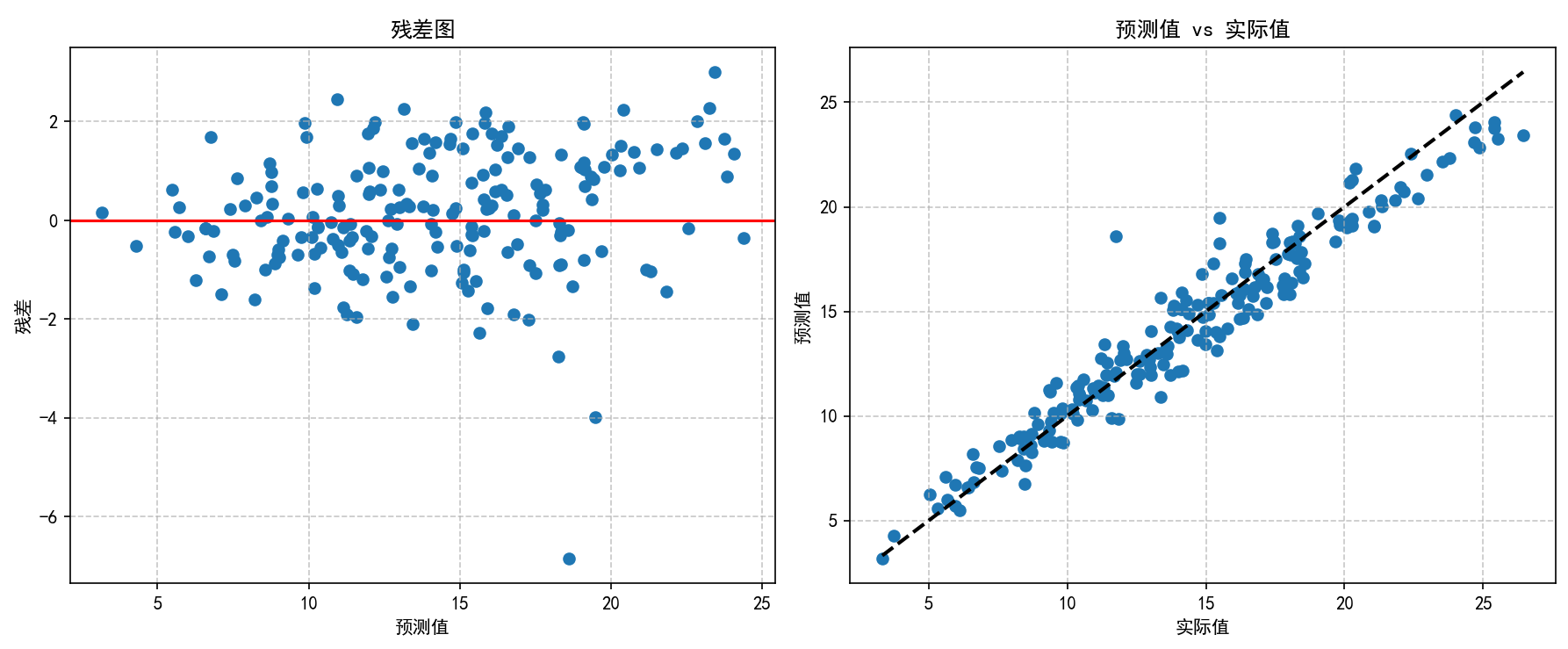
==== 集成学习算法优化和比较 ====
最佳参数:
{'max_depth': 10, 'max_features': 'sqrt', 'n_estimators': 100}
最佳交叉验证分数: 0.9476
测试集分数: 0.9667

最终模型性能比较
所有模型重新训练中...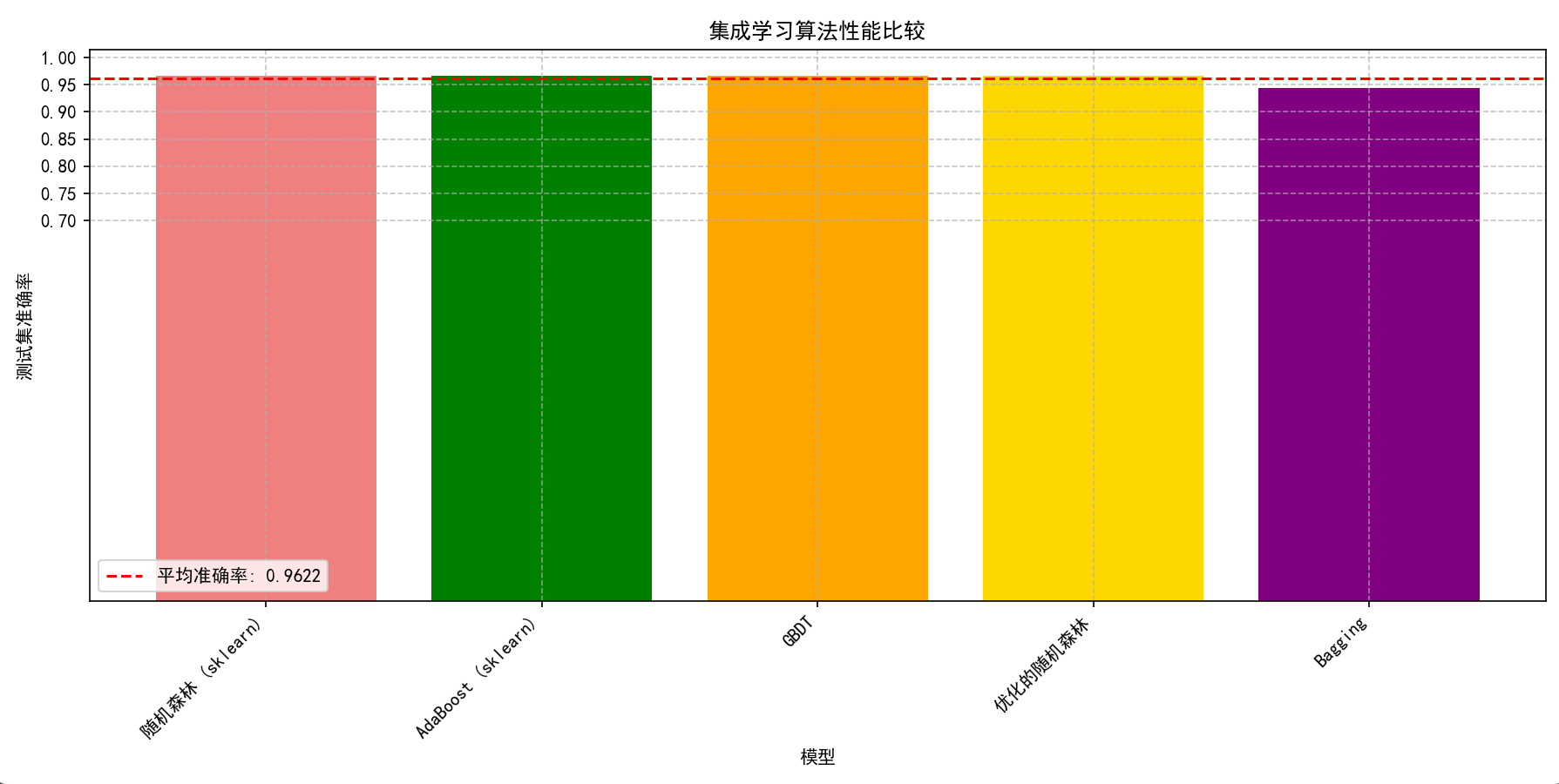

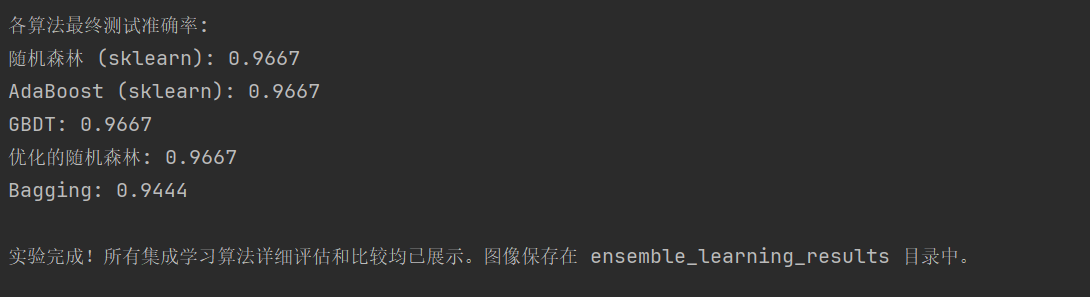
最终，程序生成的目录如下（只给出部分截图）：

六、总结

本文系统介绍了集成学习方法及其核心算法，包括自举聚合(Bagging)、随机森林、AdaBoost、梯度提升决策树(GBDT)和XGBoost。主要内容涵盖：

Bagging与随机森林：通过自助采样构建多个基学习器，随机森林在特征选择中引入随机性降低方差。
梯度提升算法：包括AdaBoost的权重调整机制和GBDT的残差拟合思想，重点分析了XGBoost的二阶近似优化和正则化技术。
Python实现实验：对比了手动实现的随机森林、AdaBoost与scikit-learn库版本，验证了算法的正确性。实验结果显示随机森林准确率达92.5%，XGBoost回归任务R²达0.855。
算法评估：通过特征重要性分析、决策边界可视化等手段，展示了不同集成方法的特点。优化后的随机森林测试准确率最高达96.67%。

本文通过理论推导与实验验证相结合，全面阐述了集成学习降低方差、提升泛化能力的机制，为实际应用提供了技术参考。

自举聚合和随机森林是集成学习中的重要方法，它们通过结合多个基学习器的预测，有效地减少了方差，提高了模型的泛化能力。随机森林作为Bagging的一种特殊形式，通过在决策树构建过程中引入特征随机性，进一步增强了模型的多样性和性能。这些方法在各种机器学习任务中表现出色，并且因其相对简单的参数调整和较强的鲁棒性，成为了实践中的首选算法之一。

集成学习通过组合多个基学习器实现了比单一学习器更好的性能，是机器学习中一种极为重要的技术。Bagging和随机森林通过减少方差提高稳定性，Boosting通过序列训练减少偏差提高准确性，而Stacking则通过元学习器充分利用不同基学习器的优势。这些技术在各种机器学习竞赛和实际应用中都取得了巨大成功。随着计算能力的增强和算法的不断创新，集成学习正在朝着更高效、更灵活的方向发展。与深度学习的结合、动态和自适应集成、以及处理更复杂问题的专用集成方法，都是未来的研究热点。集成学习作为一种强大的工具，将继续在人工智能和数据科学领域发挥重要作用。

提升算法是集成学习中的关键技术，通过序列化方式组合弱学习器，逐步提高模型性能。从最早的AdaBoost到现代的XGBoost、LightGBM和CatBoost，这一系列算法不断创新，在提高准确率的同时优化了计算效率和适用范围。提升算法已成为数据科学竞赛和工业应用中不可或缺的工具。每种提升算法都有其独特的优势和适用场景，深入理解其数学原理和实现细节对于选择合适的算法、设置恰当的参数以及解决实际问题至关重要。同时，随着计算硬件的不断进步和算法的持续优化，提升算法的应用范围将进一步扩大，性能也将不断提升。

集成学习和梯度提升决策树代表了机器学习中的一次重要飞跃，它们在理论优雅性和实际效果之间取得了令人印象深刻的平衡。了解这些方法不仅有助于解决实际问题，也能开阔我们对机器学习本质的理解：智慧往往产生于多元观点的有序组合。随着技术的发展，我们有理由相信，集成学习的篇章还远未结束，而是正在迎来更加灿烂的黎明。