当利用training data训练完模型以后，发现训练的模型的泛化能力不好，对新数据误差较大。该怎么办？该如何改进该算法？常用的有以下几种方法：

1.使用更多的训练样本

2.减小特征数量，防止出现过拟合现象

3.增特特征数

4.增加多项式，提高模型精度

5.增大/减小正则化的参数

以上几种方法，该如何选择？

一.如何评估机器学习算法的性能

如何评估

将数据集划分，一部分作为训练集，一部分作为测试集，划分比例一般为7:3。且划分最好是无序、随机的。

对于线性回归算法：首先利用training data训练集得到代价函数最小的参数，然后利用该参数计算测试集误差。

对于分类问题，即逻辑回归：步骤与线性回归相似。

该如何选择模型最合适的多项式次数？或者该如何选择正则化的参数-------》模型选择问题 模型多项式次数问题：

如下图所示，有一次项、二次项........十次项，先用training data训练参数seta，然后利用训练集测试，结果发现五次多项式的效果比较好。

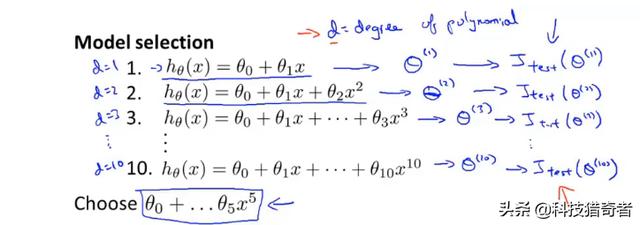
但是上述操作并不能表示该五次多项式的泛化能力好不好，因为是用的测试集选择的多项式的次数。而该次数的多项式对于线数据的泛化能力如何就不得而知了。

为了解决上述模型选择问题，通常会采用如下方法：训练集、验证集、测试集。常用比例为6:2:2

训练误差、验证误差以及测试误差表达式如下：

针对上述多项式模型选择问题。就可以用训练集训练模型，然后用验证集来选择模型，最后用测试集测试该模型的泛化误差。

二.机器学习诊断法----通过测试，发现哪里出现问题，该如何改进会比较好

1.偏差与方差 / 过拟合与欠拟合

欠拟合：训练集与测试集误差都很大

过拟合：训练集上误差小，但测试集上误差大，泛化能力不足。

偏差bias：训练集上的错误率。与训练误差成正比。

方差variance:训练集与测试集上误差的差距。与测试误差-训练误差成正比。

仍旧以上面多项式模型选择为例：当项式次数逐渐增大时，训练集误差与验证集误差如下所示：

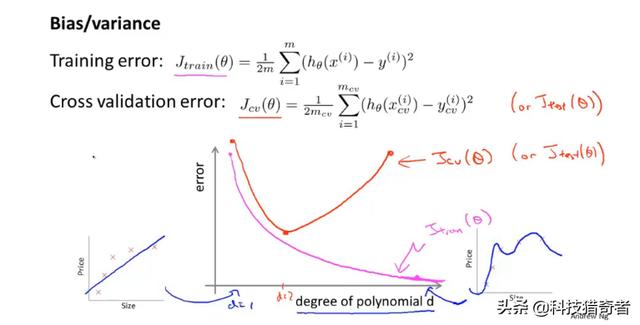
当项式次数刚开始变大时，拟合程度变好，训练集误差以及验证集误差变小，但是当项式次数变大以后，会出现过拟合现象，训练集误差变小，验证集误差变大。

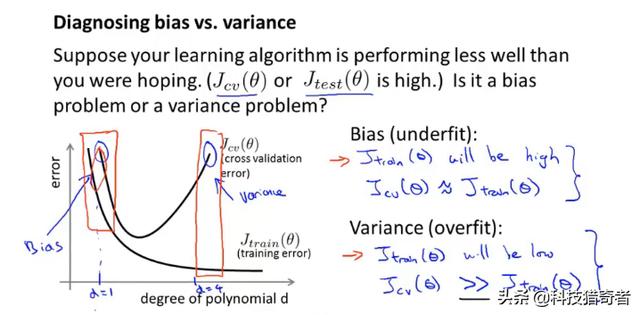
2.正则化参数与偏差/方差

正则化可以有效避免过拟合，但正则化跟算法的偏差以及方差又有什么关系了？

正则化系数较大时，为了保证代价函数最小化，需使得参数seta非常小，模型就接近直线了，当正则化参数比较小时，假设为0，则就没有正则化了，此时会出现过拟合现象。

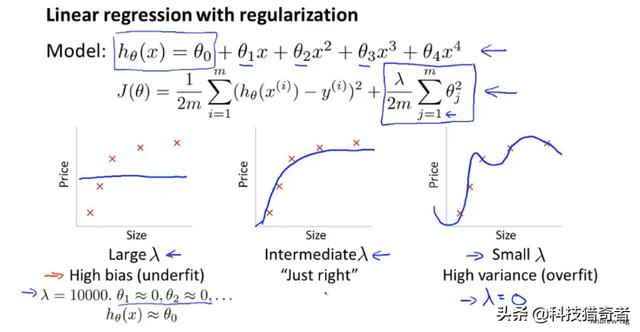
训练集、验证集以及测试集的误差表达式为：

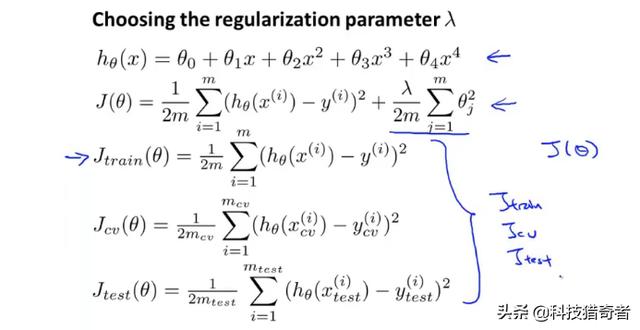
如何选择参数lamda？先用训练集训练模型，然后利用验证集选择模型

当正则化参数选择不同值时，偏差与方差的变化如下：

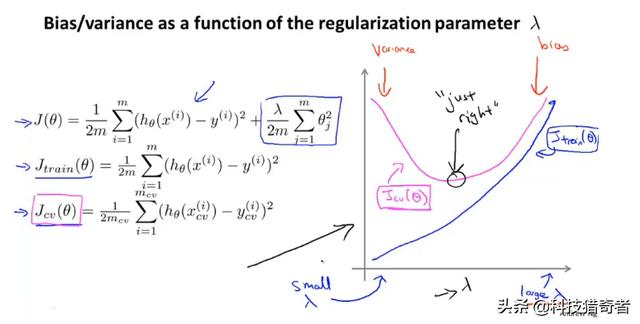
当lamda较小时，相当于没有正则化，存在过拟合现象，方差较大；当lamda较大时，会存在欠拟合现象，偏差较大。

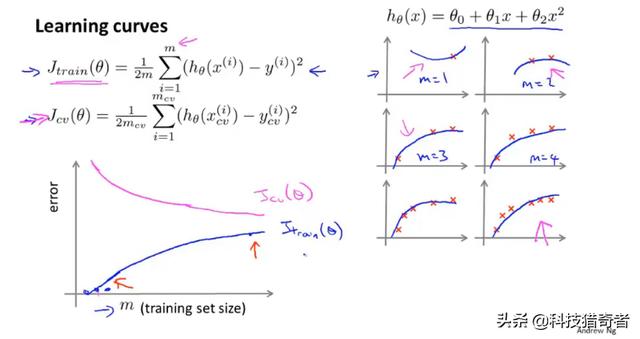
3.Learning curves 学习曲线 数据集与偏差及方差之间的关系

学习曲线是用来判断该算法是否处于偏差、方差或是二者皆有。

样本数与偏差、方差之间的关系：

高偏差：

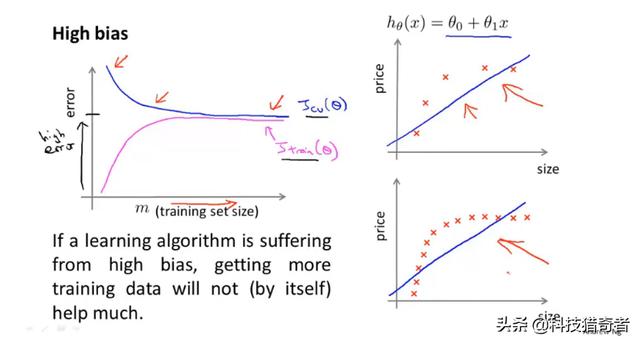
这种情况下，即使再增加样本数，偏差也不会减小。

高方差：

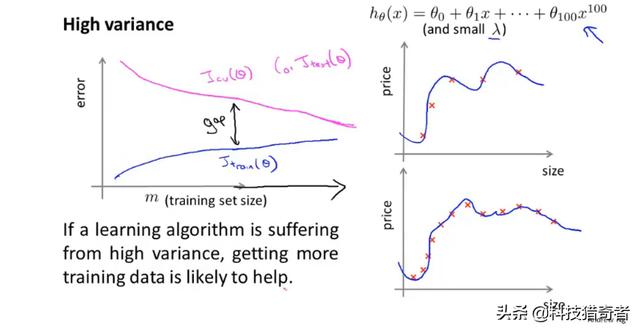
在这种高方差的情况下，增加训练数据集，对算法是有帮助的。

三：如何选择用那种方式来改进算法

第一节里面介绍了，常用的方法有以下几种：

首先先画出学习曲线-->即误差的曲线图

判断是处于高偏差还是高方差

根据高方差或者是高偏差按下图进行