Backpropagation(反向传播)，就是告诉我们用gradient descent来train一个neural network的时候该怎么做，它只是求微分的一种方法，而不是一种新的算法

Gradient Descent

gradient descent的使用方法，跟linear Regression或者是Logistic Regression是一模一样的，唯一的区别就在于当它用在neural network的时候，network parameters$\theta =w_1,w_2,\dots ,b_1,b_2,\dots$ 里面可能会有将近million个参数

但如何有效地把这个近百万维的vector给计算出来，这就是Backpropagation要做的事情，所以Backpropagation并不是一个和gradient descent不同的training的方法，它就是gradient descent，它只是一个比较有效率的算法，让你在计算这个gradient的vector的时候更有效率。

Chain Rule(链式法则)

反向传播

对整个neural network, 我们定义了一个loss function: $L(\theta )={\sum }_{n=1}^N{l}^n(\theta ),$ 它等于所有training data的loss之和。
交叉熵定义了output $y^n$和target ${\hat{y}}^n$之间的距离$l^n(\theta )$；

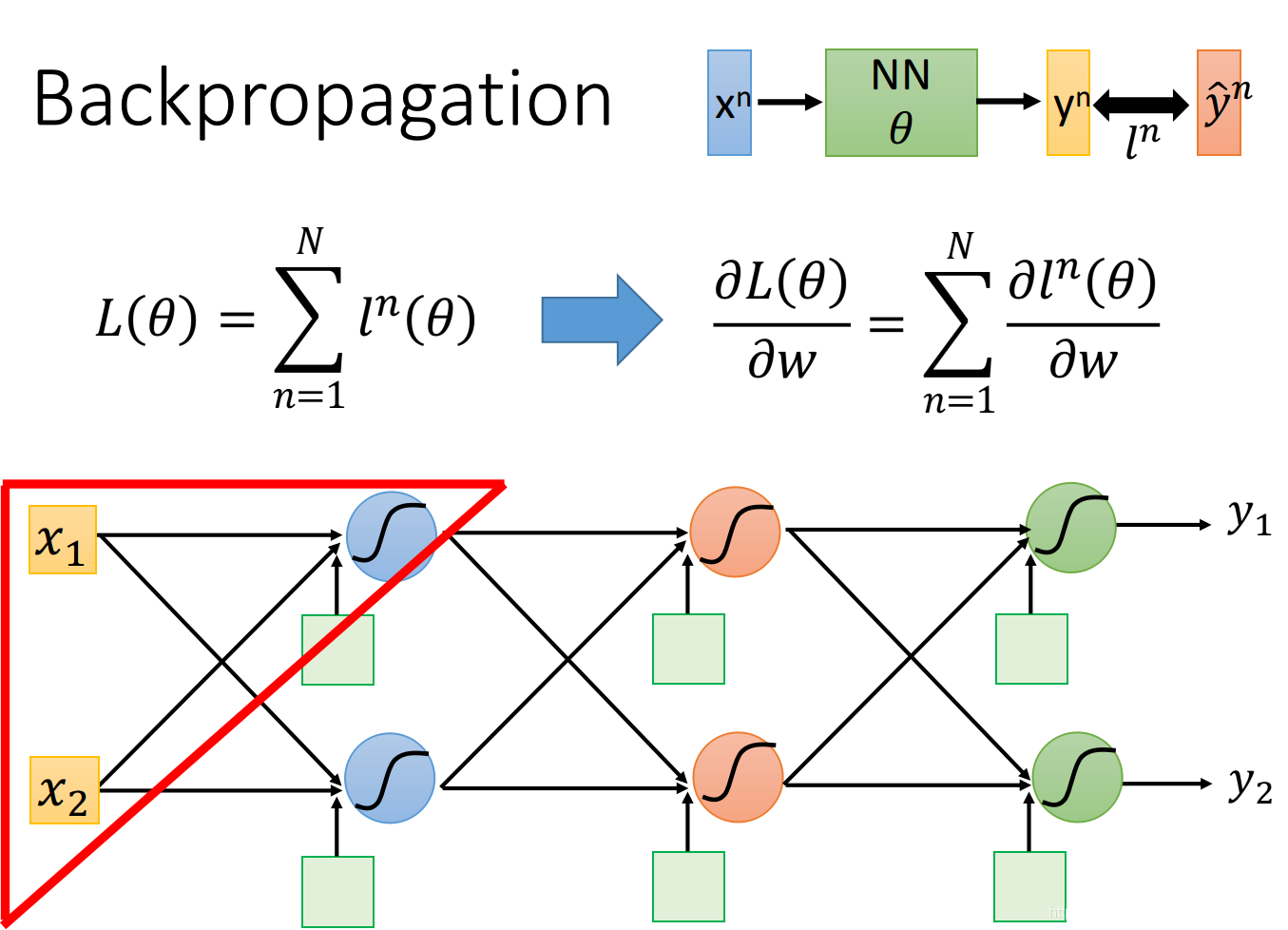
先考虑某一个neuron，先拿出上图中被红色三角形圈住的neuron，假设只有两个input $x_1,x_2$，通过这个neuron，我们先得到$z=b+w_1{x}_1+w_2{x}_2$，然后经过activation function从neuron中output出来，作为后续neuron的input，经过复杂的过程得到最终的output $y_1,y_2$
现在的问题是这样：$\frac{\partial l}{\partial w}$该怎么算？按照chain rule拆分成两项，$\frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z}$，两项分别去把它计算出来。前面一项是比较简单的，后面一项是比较复杂的

计算前面这一项$\frac{\partial z}{\partial w}$的这个process，我们称之为Forward pass；
而计算后面这项$\frac{\partial l}{\partial z}$的process，我们称之为Backward pass；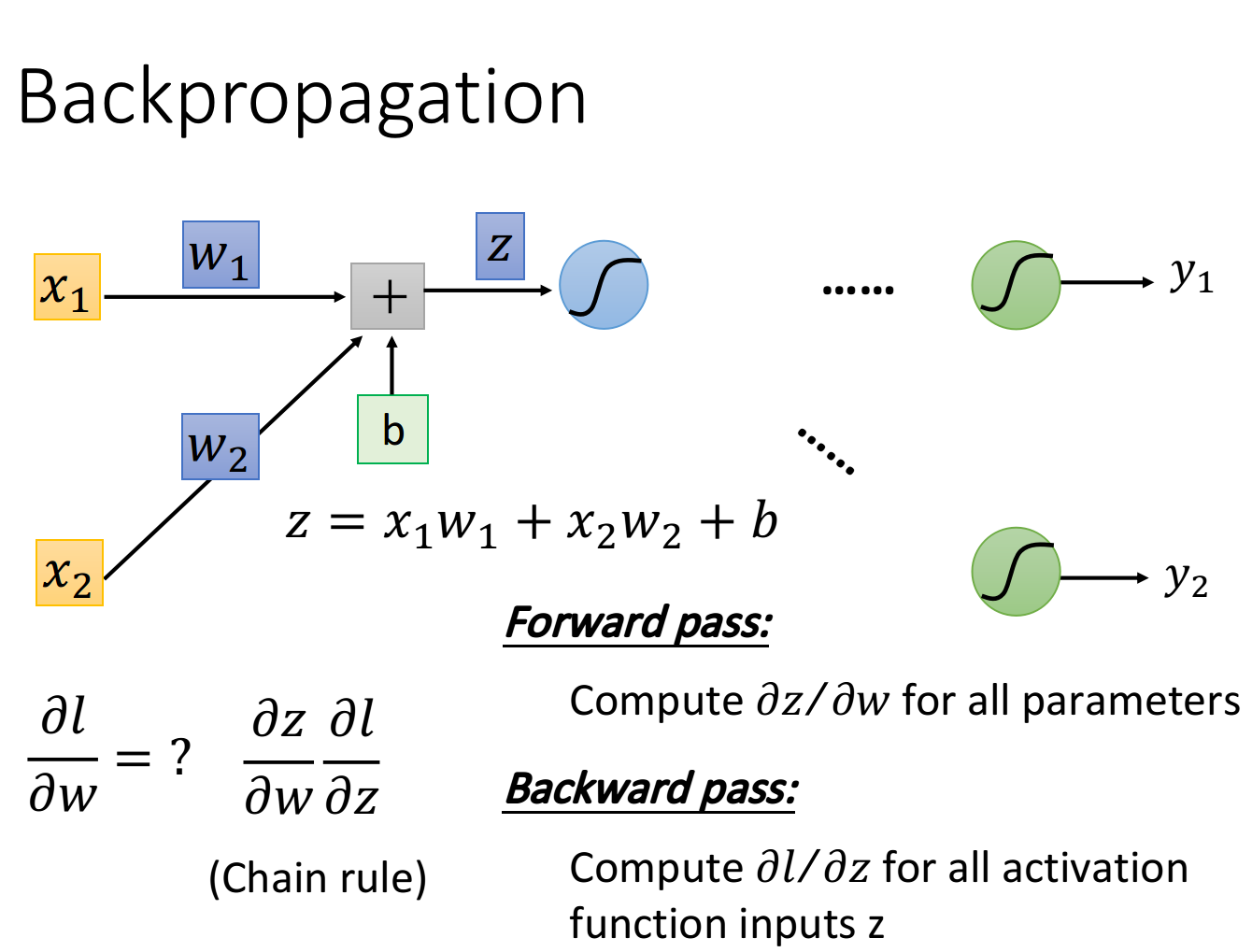

Forward pass

先考虑$\frac{\partial z}{\partial w}$这一项，秒算出来，$\frac{\partial z}{\partial w_1}=x_1,\frac{\partial z}{\partial w_2}=x_2$

规律：求$\frac{\partial z}{\partial w}$，就是看w前面连接的input是什么，那微分后的$\frac{\partial z}{\partial w}$值就是什么，因此只要计算出neural network里面每一个neuron的output就可以知道任意的z对w的偏微分

• 比如input layer作为neuron的输入时，$w_1$前面连接的是$x_1$，所以微分值就是$x_1$；$w_2$前面连接的是$x_2$，所以微分值就是$x_2$
• 比如hidden layer作为neuron的输入时，那该neuron的input就是前一层neuron的output，于是$\frac{\partial z}{\partial w}$的值就是前一层的z经过activation function之后输出的值(下图中的数据是假定activation function为sigmoid function得到的)
  

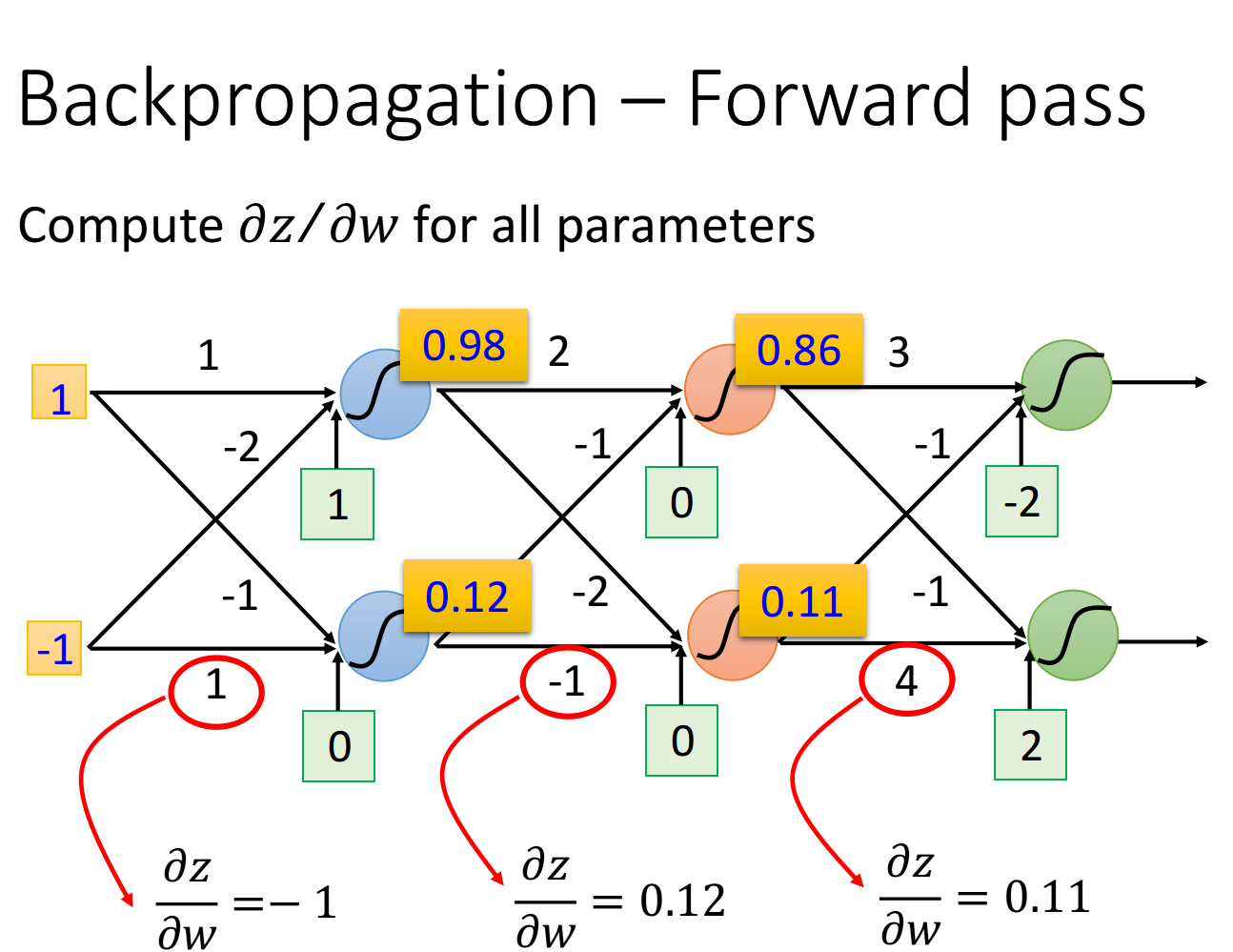
Backward pass

再考虑$\frac{\partial l}{\partial z}$这一项，它是比较复杂的，这里我们依旧假设activation function是sigmoid function

公式推导
我们的z通过activation function得到a，这个neuron的output是$a=\sigma (z)$，接下来这个a会乘上某一个weight $w_3$，再加上其它一大堆的value得到$z^{\prime }$，它是下一个neuron activation function的input，然后a又会乘上另一个weight $w_4$，再加上其它一堆value得到$z^{\prime \prime }$，后面还会发生很多很多其他事情，不过这里我们就只先考虑下一步会发生什么事情： $$\frac{\partial l}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial l}{\partial a}$$ 这里的$\frac{\partial a}{\partial z}$实际上就是activation function的微分(在这里就是sigmoid function的微分)，接下来的问题是$\frac{\partial l}{\partial a}$应该长什么样子呢？a会影响$z^{\prime }$和$z^{\prime \prime }$，而$z^{\prime }$和$z^{\prime \prime }$会影响$l$，所以通过chain rule可以得到 $$\frac{\partial l}{\partial a}=\frac{\partial z^{\prime }}{\partial a}\frac{\partial l}{\partial z^{\prime }}+\frac{\partial z^{\prime \prime }}{\partial a}\frac{\partial l}{\partial z^{\prime \prime }}$$ 这里的$\frac{\partial z^{\prime }}{\partial a}=w_3$，$\frac{\partial z^{\prime \prime }}{\partial a}=w_4$，那$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$又该怎么算呢？这里先假设我们已经通过某种方法把$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$这两项给算出来了，然后回过头去就可以把$\frac{\partial l}{\partial z}$给轻易地算出来 $$\frac{\partial l}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial l}{\partial a}={\sigma }^{\prime }(z)[w_3\frac{\partial l}{\partial z^{\prime }}+w_4\frac{\partial l}{\partial z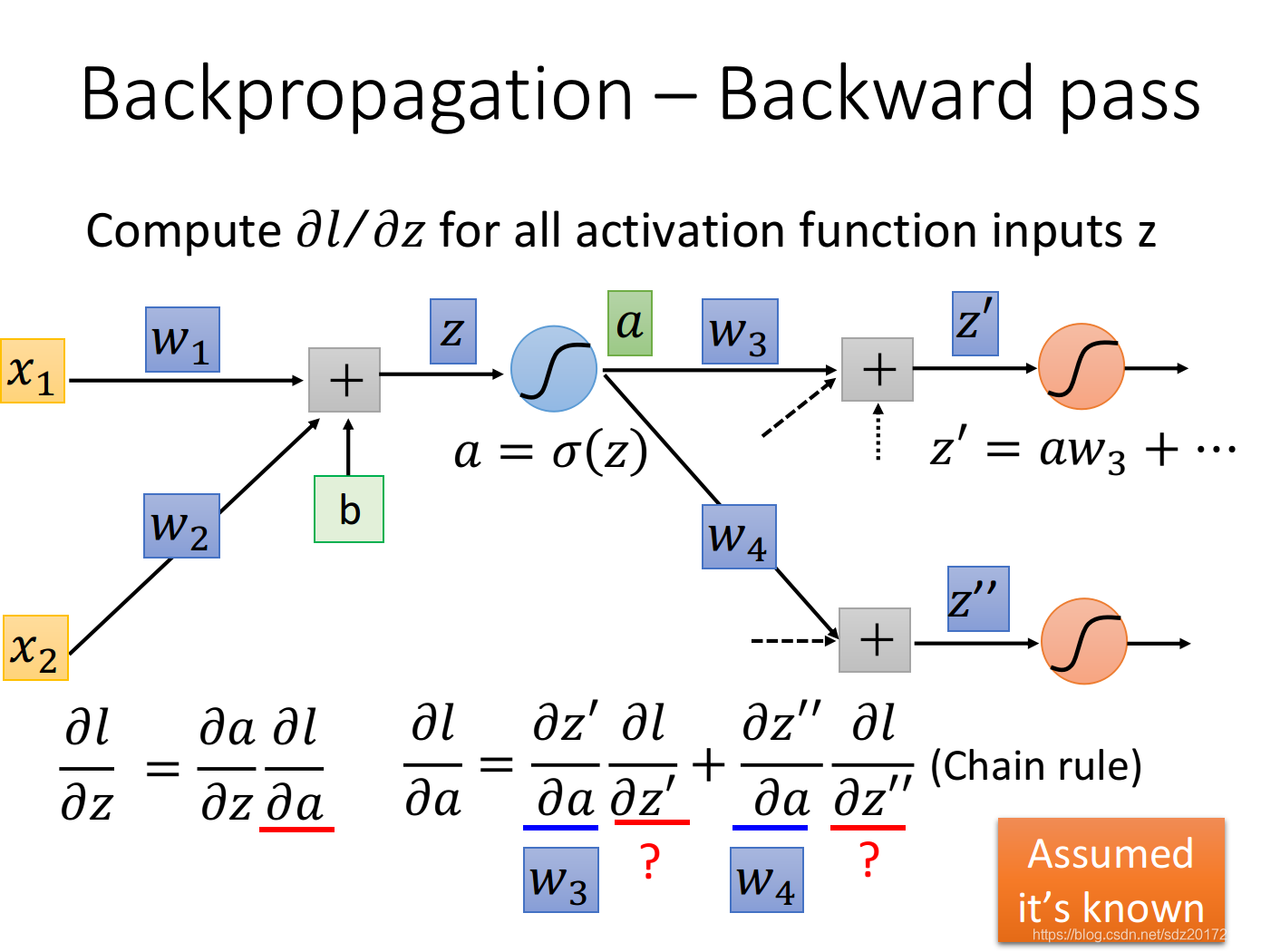^{\prime \prime }}]$$

另一个观点

这个式子还是蛮简单的，然后，我们可以从另外一个观点来看待这个式子

你可以想象说，现在有另外一个neuron，它不在我们原来的network里面，在下图中它被画成三角形，这个neuron的input就是$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$，那input $\frac{\partial l}{\partial z^{\prime }}$就乘上$w_3$，input $\frac{\partial l}{\partial z^{\prime \prime }}$就乘上$w_4$，它们两个相加再乘上activation function的微分 ${\sigma }^{\prime }(z)$，就可以得到output $\frac{\partial l}{\partial z}$

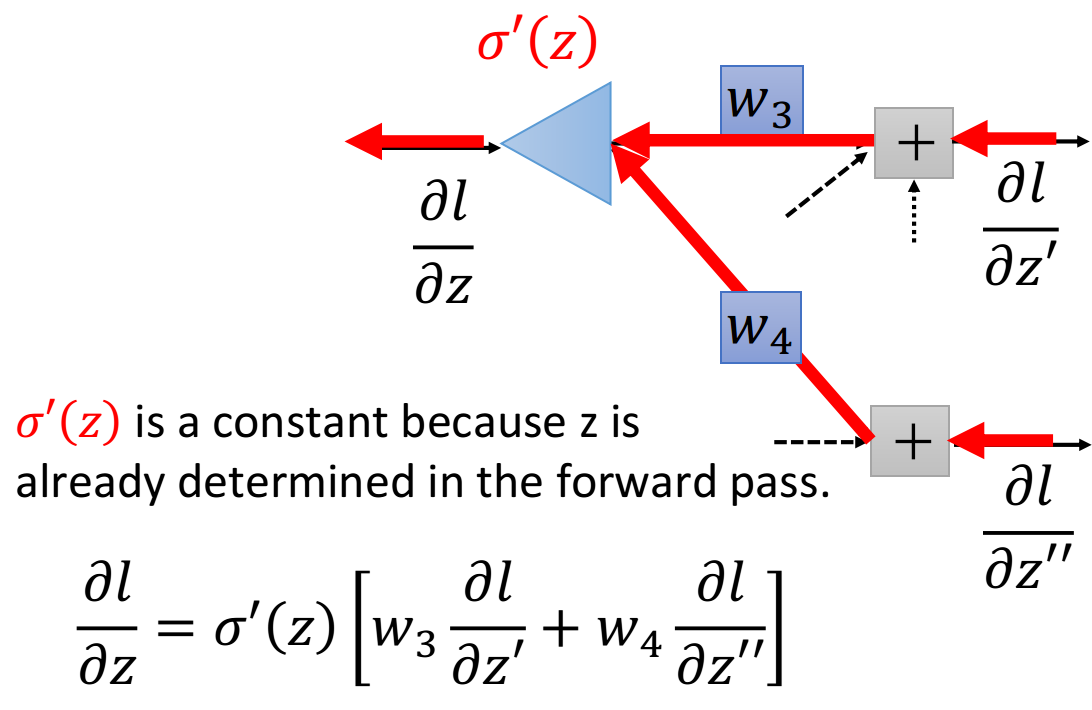
这张图描述了一个新的“neuron”，它的含义跟图下方的表达式是一模一样的，作这张图的目的是为了方便理解
值得注意的是，这里的${\sigma }^{\prime }(z)$是一个constant常数，它并不是一个function，因为z其实在计算forward pass的时候就已经被决定好了，z是一个固定的值

所以这个neuron其实跟我们之前看到的sigmoid function是不一样的，它并不是把input通过一个non-linear进行转换，而是直接把input乘上一个constant ${\sigma }^{\prime }(z)$，就得到了output，因此这个neuron被画成三角形，代表它跟我们之前看到的圆形的neuron的运作方式是不一样的，它是直接乘上一个constant(这里的三角形有点像电路里的运算放大器op-amp，它也是乘上一个constant)

两种情况

ok，现在我们最后需要解决的问题是，怎么计算$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$这两项，假设有两个不同的case：

case 1：Output Layer

假设蓝色的这个neuron已经是hidden layer的最后一层了，也就是说连接在$z^{\prime }$和$z^{\prime \prime }$后的这两个红色的neuron已经是output layer，它的output就已经是整个network的output了，这个时候计算就比较简单 $$\frac{\partial l}{\partial z^{\prime }}=\frac{\partial y_1}{\partial z^{\prime }}\frac{\partial l}{\partial y_1}$$ 其中$\frac{\partial y_1}{\partial z^{\prime }}$就是output layer的activation function (softmax) 对$z^{\prime }$的偏微分

而$\frac{\partial l}{\partial y_1}$就是loss对$y_1$的偏微分，它取决于你的loss function是怎么定义的，也就是你的output和target之间是怎么evaluate的，你可以用cross entropy，也可以用mean square error，用不同的定义，$\frac{\partial l}{\partial y_1}$的值就不一样

这个时候，你就已经可以把$l$对$w_1$和$w_2$的偏微分$\frac{\partial l}{\partial w_1}$、$\frac{\partial l}{\partial w_2}$算出来了

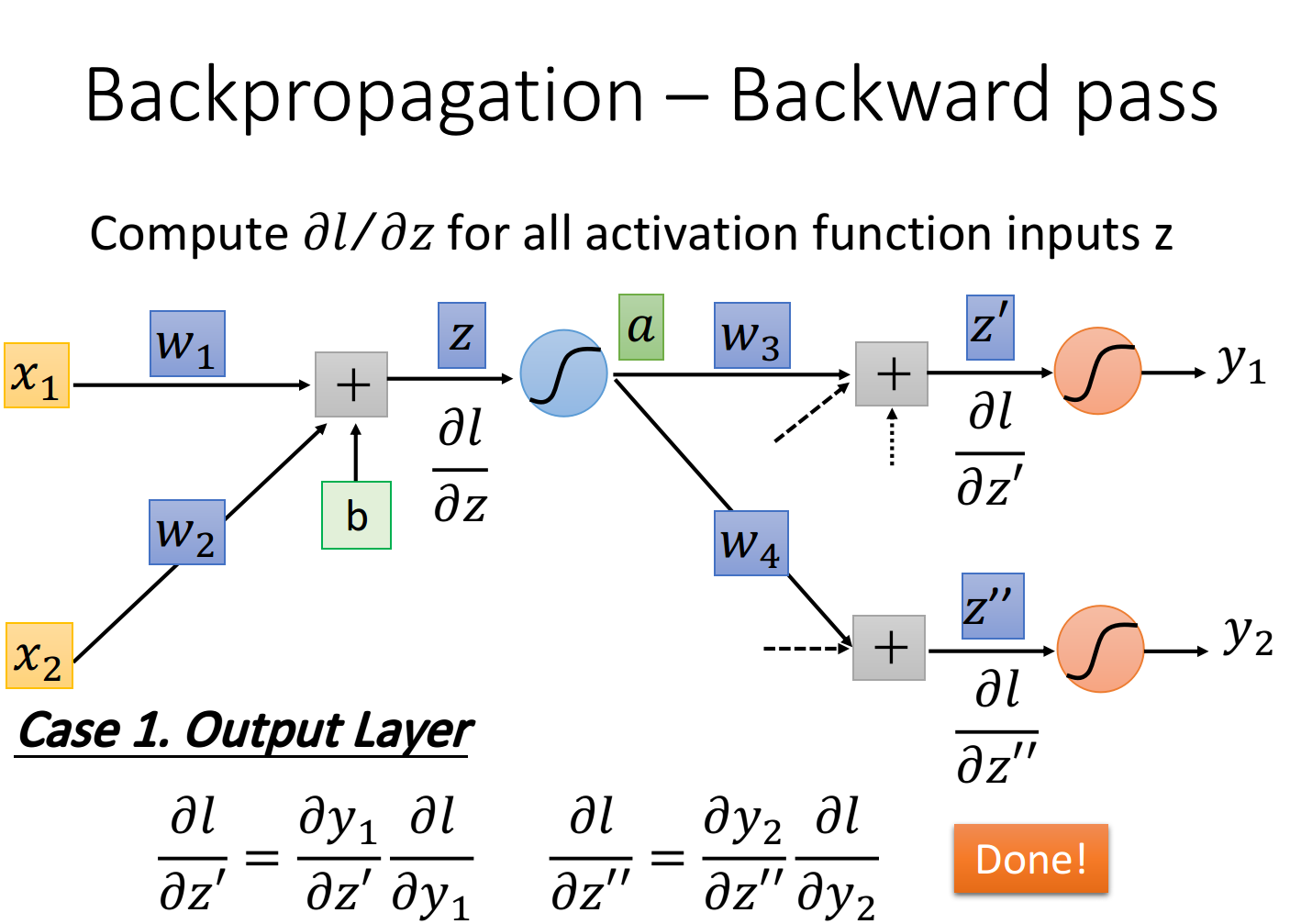
Case 2：Not Output Layer

假设现在红色的neuron并不是整个network的output，那$z^{\prime }$经过红色neuron的activation function得到$a^{\prime }$，然后output $a^{\prime }$和$w_5$、$w_6$相乘并加上一堆其他东西分别得到$z_a$和$z_b$，如下图所示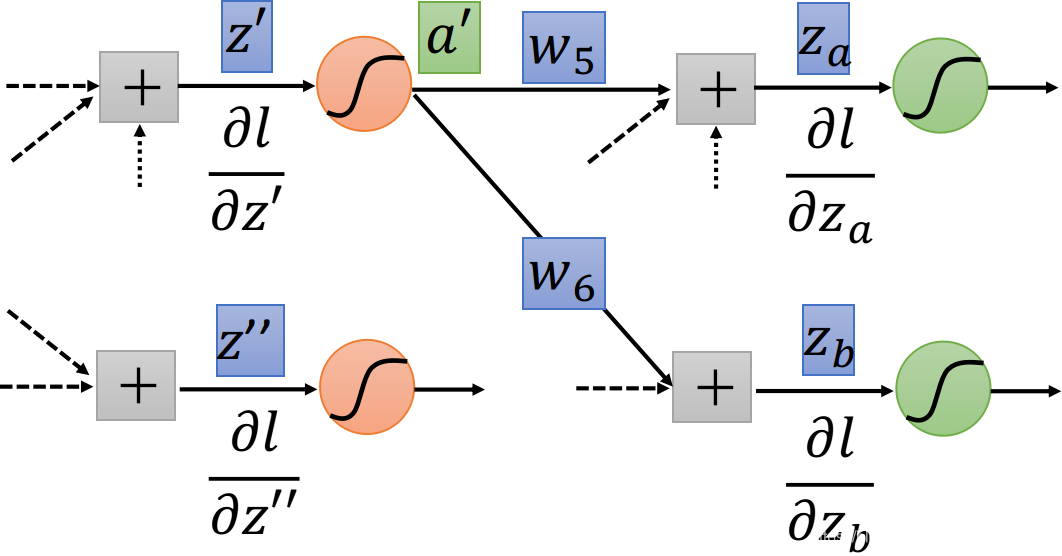

根据之前的推导证明类比，如果知道$\frac{\partial l}{\partial z_a}$和$\frac{\partial l}{\partial z_b}$，我们就可以计算$\frac{\partial l}{\partial z^{\prime }}$，如下图所示，借助运算放大器的辅助理解，将$\frac{\partial l}{\partial z_a}$乘上$w_5$和$\frac{\partial l}{\partial z_b}$乘上$w_6$的值加起来再通过op-amp，乘上放大系数${\sigma }^{\prime }(z^{\prime })$，就可以得到output $\frac{\partial l}{\partial z^{\prime }}$ $$\frac{\partial l}{\partial z^{\prime }}={\sigma }^{\prime }(z^{\prime })[w_5\frac{\partial l}{\partial z_a}+w_6\frac{\partial l}{\partial z_b}]$$

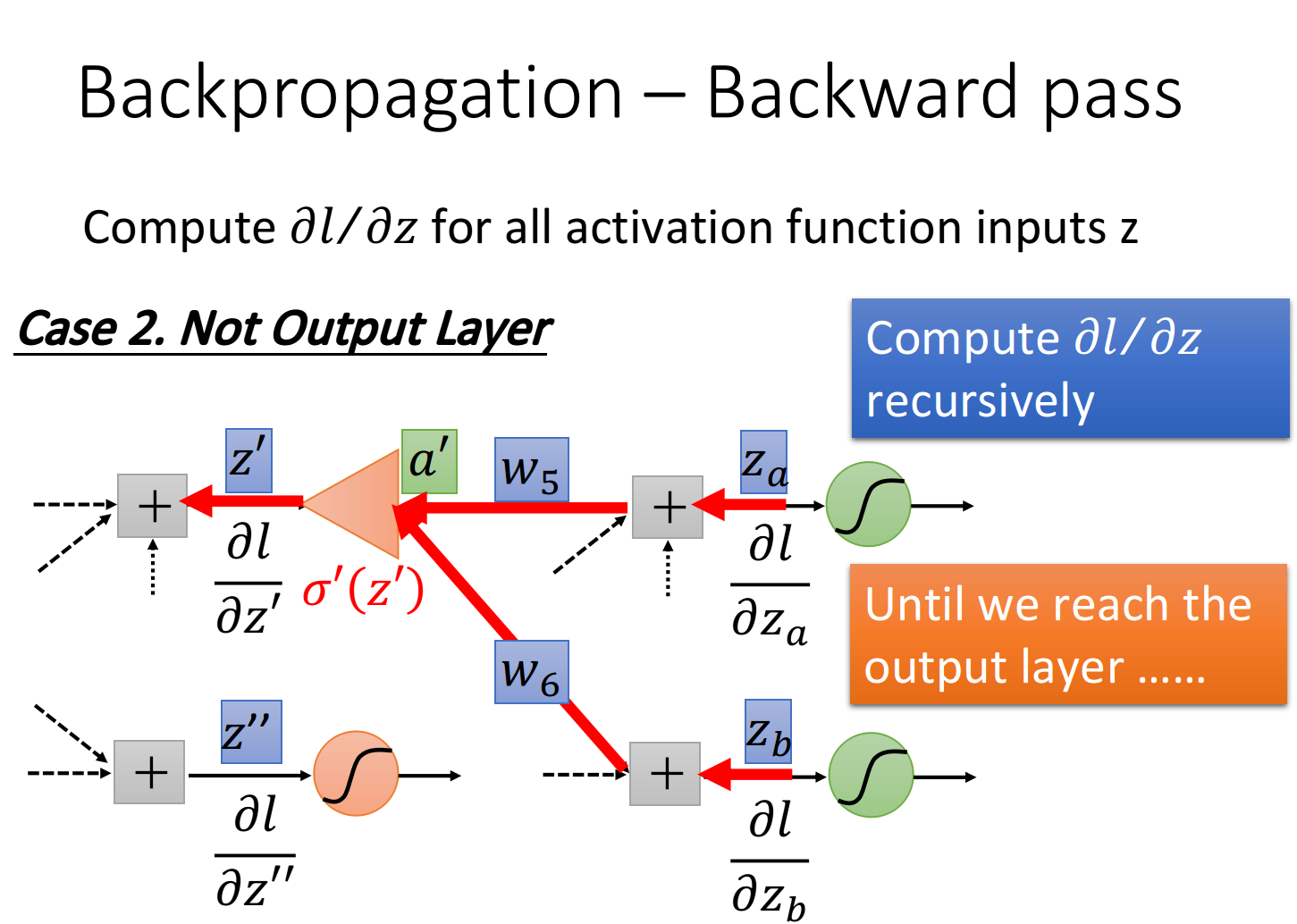
知道$z^{\prime }$和$z^{\prime \prime }$就可以知道$z$，知道$z_a$和$z_b$就可以知道$z^{\prime }$，… ，现在这个过程就可以反复进行下去，直到找到output layer，我们可以算出确切的值，然后再一层一层反推回去
你可能会想说，这个方法听起来挺让人崩溃的，每次要算一个微分的值，都要一路往后走，一直走到network的output，如果写成表达式的话，一层一层往后展开，感觉会是一个很可怕的式子，但是！实际上并不是这个样子做的

你只要换一个方向，从output layer的$\frac{\partial l}{\partial z}$开始算，你就会发现它的运算量跟原来的network的Feedforward path其实是一样的

假设现在有6个neuron，每一个neuron的activation function的input分别是$z_1$、$z_2$、$z_3$、$z_4$、$z_5$、$z_6$，我们要计算$l$对这些$z$的偏微分，按照原来的思路，我们想要知道$z_1$的偏微分，就要去算$z_3$和$z_4$的偏微分，想要知道$z_3$和$z_4$的偏微分，就又要去计算两遍$z_5$和$z_6$的偏微分，因此如果我们是从$z_1$、$z_2$的偏微分开始算，那就没有效率

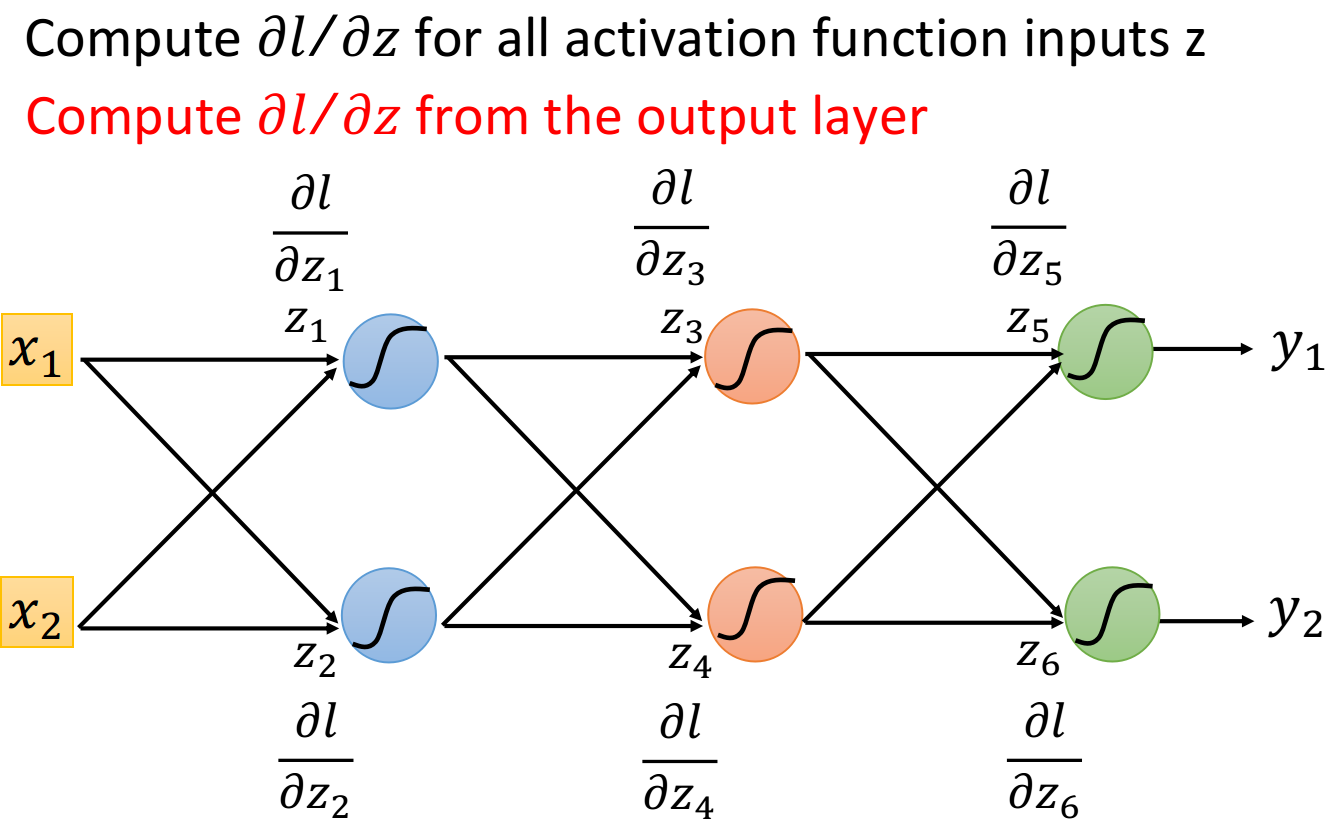
但是，如果你反过来先去计算$z_5$和$z_6$的偏微分的话，这个process，就突然之间变得有效率起来了，我们先去计算$\frac{\partial l}{\partial z_5}$和$\frac{\partial l}{\partial z_6}$，然后就可以算出$\frac{\partial l}{\partial z_3}$和$\frac{\partial l}{\partial z_4}$，最后就可以算出$\frac{\partial l}{\partial z_1}$和$\frac{\partial l}{\partial z_2}$，而这一整个过程，就可以转化为op-amp运算放大器的那张图

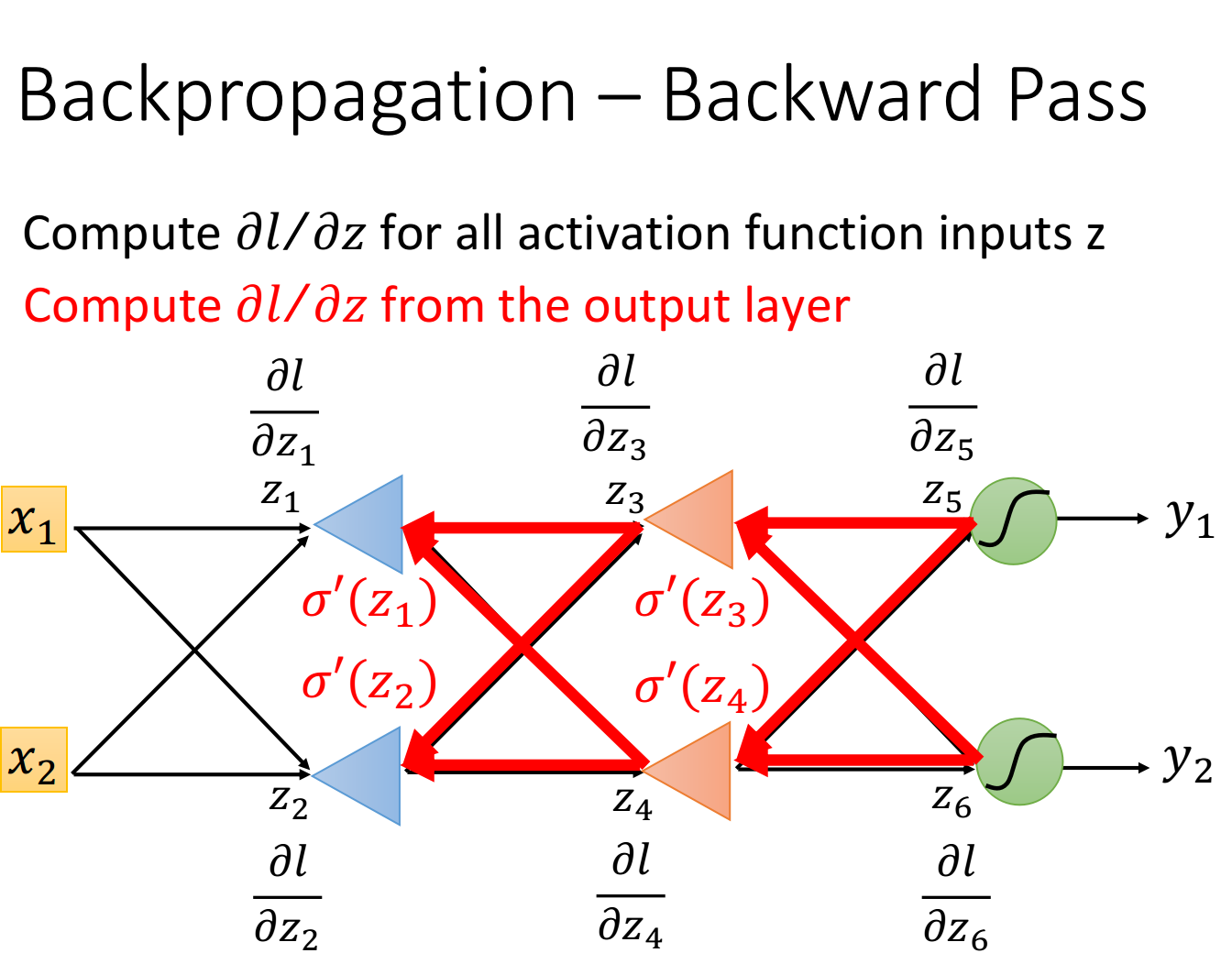
这里每一个op-amp的放大系数就是${\sigma }^{\prime }(z_1)$、${\sigma }^{\prime }(z_2)$、${\sigma }^{\prime }(z_3)$、${\sigma }^{\prime }(z_4)$，所以整一个流程就是，先快速地计算出$\frac{\partial l}{\partial z_5}$和$\frac{\partial l}{\partial z_6}$，然后再把这两个偏微分的值乘上路径上的weight汇集到neuron上面，再通过op-amp的放大，就可以得到$\frac{\partial l}{\partial z_3}$和$\frac{\partial l}{\partial z_4}$这两个偏微分的值，再让它们乘上一些weight，并且通过一个op-amp，就得到$\frac{\partial l}{\partial z_1}$和$\frac{\partial l}{\partial z_2}$这两个偏微分的值，这样就计算完了，这个步骤，就叫做Backward pass
在做Backward pass的时候，实际上的做法就是建另外一个neural network，本来正向neural network里面的activation function都是sigmoid function，而现在计算Backward pass的时候，就是建一个反向的neural network，它的activation function就是一个运算放大器op-amp，每一个反向neuron的input是loss $l$对后面一层layer的$z$的偏微分$\frac{\partial l}{\partial z}$，output则是loss $l$对这个neuron的$z$的偏微分$\frac{\partial l}{\partial z}$，做Backward pass就是通过这样一个反向neural network的运算，把loss $l$对每一个neuron的$z$的偏微分$\frac{\partial l}{\partial z}$都给算出来

注：如果是正向做Backward pass的话，实际上每次计算一个$\frac{\partial l}{\partial z}$，就需要把该neuron后面所有的$\frac{\partial l}{\partial z}$都给计算一遍，会造成很多不必要的重复运算，如果写成code的形式，就相当于调用了很多次重复的函数；而如果是反向做Backward pass，实际上就是把这些调用函数的过程都变成调用“值”的过程，因此可以直接计算出结果，而不需要占用过多的堆栈空间

Summary

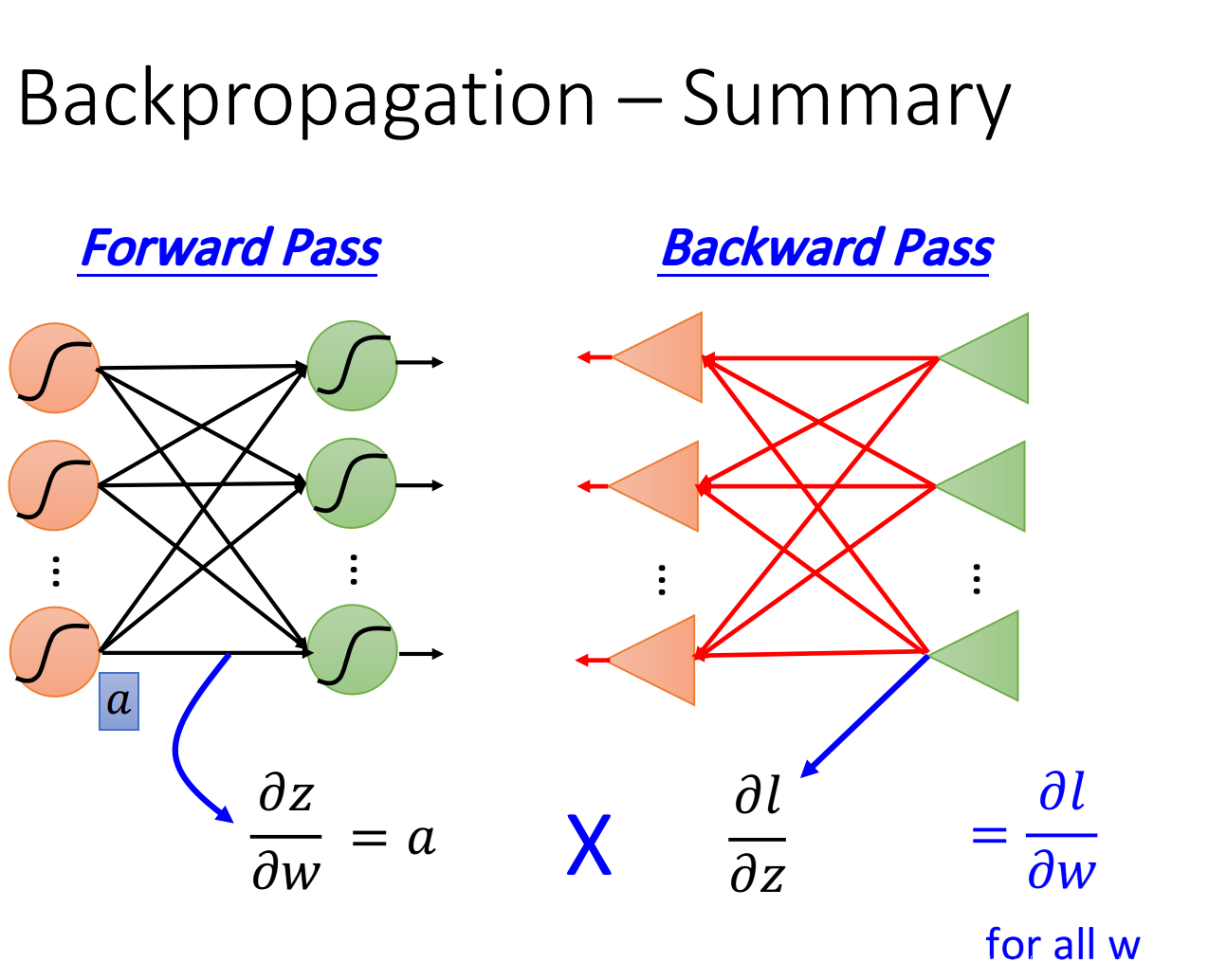
Forward pass，每个neuron的activation function的output，就是它所连接的weight的$\frac{\partial z}{\partial w}$

Backward pass，建一个与原来方向相反的neural network，它的三角形neuron的output就是$\frac{\partial l}{\partial z}$

把通过forward pass得到的$\frac{\partial z}{\partial w}$和通过backward pass得到的$\frac{\partial l}{\partial z}$乘起来就可以得到$l$对$w$的偏微分$\frac{\partial l}{\partial w}$ $$\frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}|forwardpass\cdot \frac{\partial l}{\partial z}|backwardpass$$