机器学习：感知机算法（PLA）

感知机（Perceptron）是一种最简单的人工神经网络模型，由弗兰克·罗森布拉特（Frank Rosenblatt）在1958年提出。它是一种线性分类器，用于二分类任务，即把输入数据分为两个类别。

燕双嘤

4618人浏览 · 2021-11-07 16:52:31

燕双嘤 · 2021-11-07 16:52:31 发布

1，概述

1.1，定义

感知机（Perceptron）：

二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1；

感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型；

感知机学习旨在求出将训练数据进行现行划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。

感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式；

感知机的缺点：我们在不知道数据的情况下（是否线性可分）PLA就不会停下来，这个时候我们会使用Pocket演算法来找到一根不错的直线。Pocket演算法的基本思想就是找到一根犯错误更小的直线。实务上我们一般会执行到一定的时间或者一定的步数就会停下来。结果是它是一条不错的线，但是可能不是一个最优解。

1.2，感知机模型

假设输入空间（特征空间）是 $X\subseteq R^n$ ，输出空间是 $y=\left \{ +1,-1 \right \}$ 。输入 $x\in X$ 表示实例的特征向量，对应输入空间（特征空间）的点，输出 $y\in Y$ 表示实例的类别。由输入空间到输出空间的函数：

感知机： $f(x)=sign(w*x+b)$

$w,b$ 为模型参数， $w\in R^n$ 叫做权值或权值向量， $b\in R$ 叫作偏执。

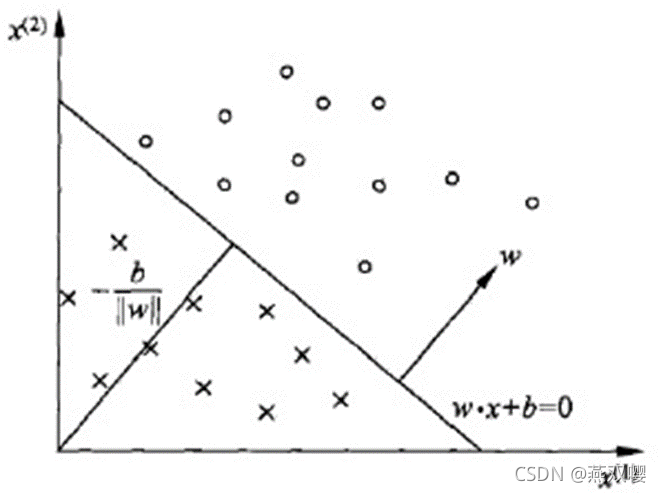
符号函数： $sign(x)=\begin{Bmatrix} +1,x\geqslant 0\\-1,x< 0 \end{Bmatrix}$

1.3，几何解释

感知机可以理解为几何中的线性方程： $w*x+b=0$ 对应于特征空间 $R^n$ 中的一个超平面 $S$ ，其中 $w$ 是超平面法向量， $b$ 是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点（特征向量）分别被分为正、负两类。

2，学习策略

2.1，损失函数

假设训练集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型参数 $w,b$ ，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。

损失函数的一个自然选择是误分类点的总数。但是，这样的损失函数不是参数 $w,b$ 的连续可导函数，不易优化。损失函数的另外一个选择是误分类点到超平面 $S$ 的总距离，这是感知机所采用的。为此，首先定义输入空间 $R^n$ 中任一点 $x_0$ 到超平面 $S$ 的距离：

$\frac{|w^T*x_0+b|}{||w||}$

其次，对于误分类的数据 $(x_i,y_i)$ 来说：

$y_i(w^T*x_i+b)<0$

因为： $y_i(w^T*x_i+b)>0,\begin{Bmatrix} y_i=+1,w^T*x+b>0\\ y_i=-1,w^T*x+b<0 \end{Bmatrix}$

因此，误分类点到平面 $S$ 的距离：

$-\frac{y_i(w^T*x_i+b)}{||w||}$

这样，假设超平面 $S$ 的误分类点集合为 $M$ ，那么所有误分类点到超平面 $S$ 的总距离为：

$-\frac{1}{||w||}\sum_{x_i\in M}^{}y_i(w^T*x_i+b)$

不考虑 $\frac{1}{||w||}$ ，就得到感知机学习的损失函数：

$L(w,b)=-\sum_{x_i\in M}^{}y_i(w^T*x_i+b)$

原因：

$\frac{1}{||w||}$ 不影响 $y_i(w^T*x_i+b)$ 正负的判断，即不影响学习算法的中间过程。因为感知机学习算法是误分类驱动的，这里需要注意的是所谓的“误分类驱动”指的是我们只需要判断 $y_i(w^T*x_i+b)$ 的正负来判断分类的正确与否，而 $\frac{1}{||w||}$ 并不影响正负值的判断。所以 $\frac{1}{||w||}$ 对感知机学习算法的中间过程可以不考虑。

$\frac{1}{||w||}$ 不影响感知机学习算法的最终结果。因为感知机学习算法最终的终止条件是所有的输入都被正确分类，即不存在误分类的点。则此时损失函数为0 对应于 $-\frac{1}{||w||}\sum_{x_i\in M}^{}y_i(w^T*x_i+b)$ ，即分子为0。则可以看出 $\frac{1}{||w||}$ 对最终结果也无影响。

总结：PLA的任务是进行二分类工作，它最终并不关心得到的超平面离各点的距离有多少，关心误分类点的数量，而SVM则关心距离。

由于 $y_i(w^T*x_i+b)<0$ 所以 $L(w,b)$ 是非负的。如果没有误分类点，损失函数值为0。而且由于误分类点越少，误分类点里超平面越近，损失函数值就越小（求和数目减少）。一个特定的样本点的损失函数：在误分类时是参数 $w,b$ 的线性函数，在正确分类时是0。因此，给定训练数据集 $T$ ，损失函数 $L(w,b)$ 是 $w,b$ 的连续可导函数。

因此感知学习的策略是在假设空间中选取使损失函数 $L(w,b)$ 最小的模型参数 $w,b$ ，即感知机损失函数目标：

$\underset{min}{L(w,b)}=min(-\sum_{x_i\in M}^{}y_i(w^T*x_i+b))$

2.2，优化函数

首先，任意选取一个超平面 $w_0, b_0$ ，然后用梯度下降法不断极小化目标函数 $\underset{min}{L(w,b)}$ 。极小化的过程不是一次使 $M$ 中所有误分类点的梯度下降，而是一次又一次随机选取一个误分类点使其梯度下降。

假设误分类点集合 $M$ 是固定的，那么损失函数 $L(w,b)$ 的梯度：

$\Delta_wL(w,b) = -\sum_{x_i\in M}y_ix_i$

$\Delta_bL(w,b) = -\sum_{x_i\in M}y_i$

因此，需要沿着梯度的反方向更新 $w,b$ ，进而可以得出：

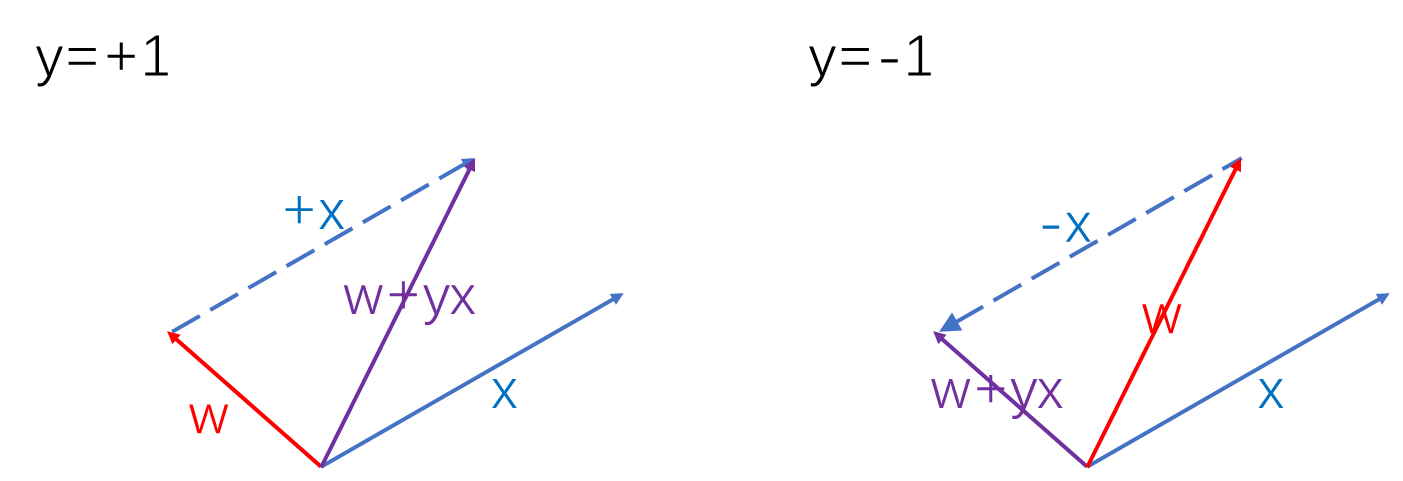
随机采取一个误分类点 $(x_n(t),y_n(t))$ ，对 $w,b$ 进行更新：

$w_{t+1}=w_{t}+y_n(t)x_n(t)$

$b_{t+1}=b_t+y_n(t)$

采用这种方法的原因：简单。但不限于这一种方法。

修正：

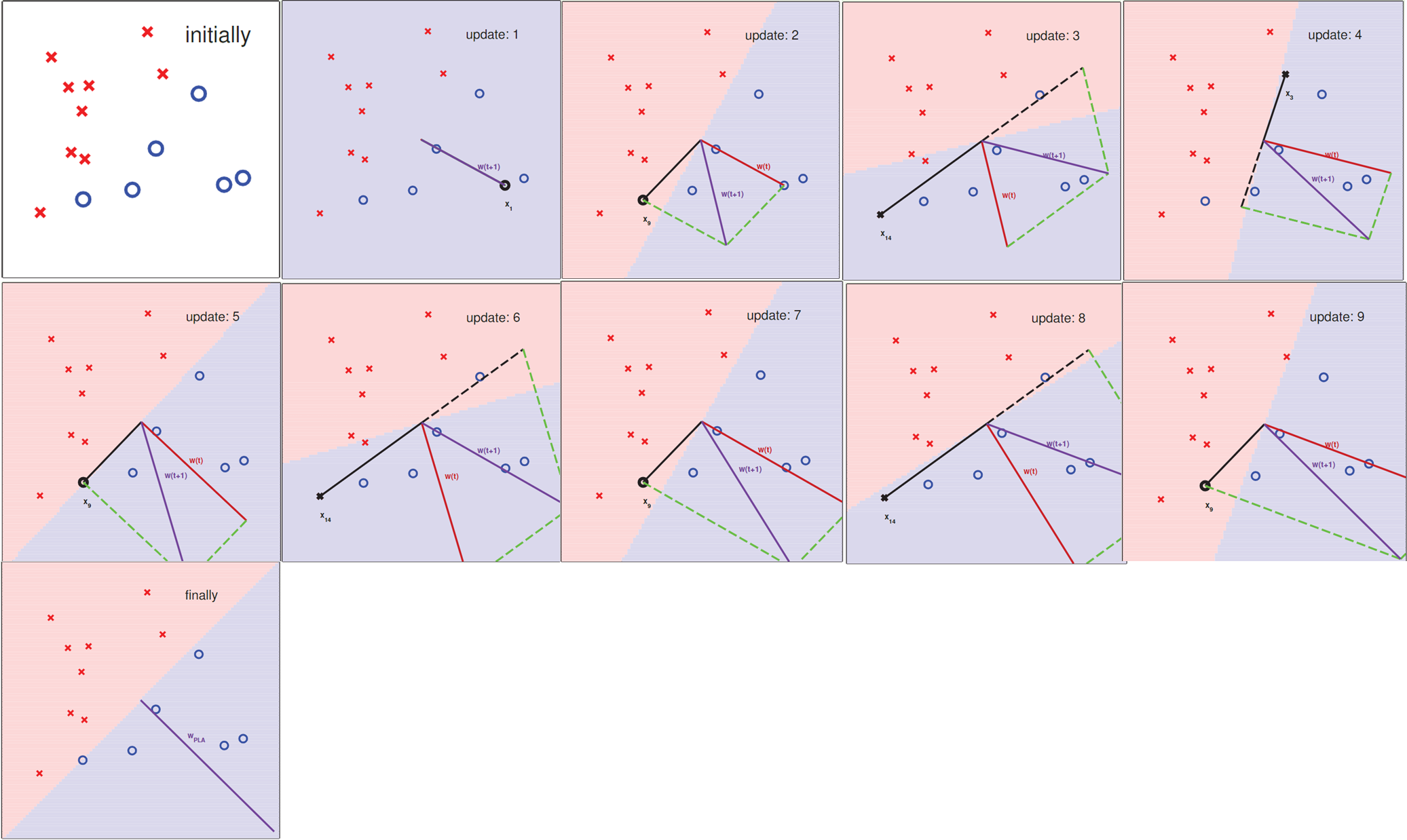
整体修正过程：

3，收敛性

3.1，向量持续修正

每次修改后的 $w$ 向量逐渐趋向于最终的完美的 $w_f$ （向量的乘积不断变大）：

更新： $w_{t+1}=w_{t}+y_n(t)x_n(t)$

缩放： $y_{n(t)}w_f^Tx_{n(t)}\geqslant \underset{n}{min}y_nw_f^Tx_n$

线性可分：存在 $w_f$ 使得， $y_n=sign(w_f^Tx_n)$

在标准感知机中通常会省略 $b$ ，融入 $x$ 中，即：

$x^{'}_n=\begin{bmatrix} x_n\\ 1 \end{bmatrix}$ $w^{'}=\begin{bmatrix} w\\ b \end{bmatrix}$

完美的 $w_f$ 下不会分类错误： $\underset{n}{min}\left ( y_nw_f^Tx_n \right )> 0$ 。

$w_f^Tw_{t+1}=w_f^T(w_t+y_{n(t)}x_{n(t)})$

$\geqslant w_f^Tw_t+\underset{n}{min}y_nw_f^Tx_n$

$>w_f^Tw_t+0 =w_f^Tw_t$

确实发现它们的内积在不断地增大，内积的增大原因有向量的模长在增大或者是夹角在变小。但是证明两个向量的相关性增大需要证明的是两个向量的夹角在变小，所以需要排除向量模长的不确定性。

3.2，修正幅度上限

在这个推导中，更加关心的是 $w$ 与 $w_f$ （最终的 $w$ )之间的角度，观察分类错误的点：

$||w_{t+1}||^2 = ||w_t+y_{n(t)}x_{n(t)}||^2$

$=||w_t||^2+2y_{n(t)}w_t^Tx_{n(t)}+||y_{n(t)}x_{n(t)}||^2$

$\leqslant ||w_t||^2+0+||y_{n(t)}x_{n(t)}||^2$

$\leqslant ||w_t||^2+\underset{n}{max}||y_nx_n||^2$

即：

$||w_t+1||^2 \leqslant ||w_t||^2+\underset{n}{max}||y_nx_n||^2$

$||w_{t+1}||^2 - ||w_{t}||^2 \leqslant\underset{n}{max}||y_nx_n||^2$

修正之后权向量的长度，相较于修正之前的增加有一个上限，或者说它的长度增长是较慢的。这个上限由 $S$ 中距离坐标原点最远的那个点决定，所以 $w_t$ 和 $w_{t+1}$ 差别不会太大，所以现在还不能证明夹角在变小。

3.3，优化证明

用 $w_f$ 与 $w_t$ 的模向量直接相乘（乘出来的结果即为两个向量的角度），

即： $cos\theta =\displaystyle \frac{w_f^T}{||w_f||}\frac{w_t}{||w_t||}$ 的值的变化

过程如下：

由前面可知， $w$ 更新： $w_{t+1}=w_{t}+y_{n(t)}x_{n(t)}$

$w_f^Tw_t=w_f^T(w_{t-1}+y_{n(t-1)}x_{n(t-1)})$

$\geqslant w_f^Tw_{t-1}+\underset{n}{min}\, y_nw_f^Tx_n$

$\geqslant w_f^Tw_0+T*\underset{n}{min}\, y_nw_f^Tx_n$

$\geqslant T*\underset{n}{min}\, y_nw_f^Tx_n$

即： $w_f^Tw_t \geqslant T*\underset{n}{min}\, y_nw_f^Tx_n$

-----------------------------------------------------------------------------------

$||w_t||^2=||w_{t-1}+y_{n(t-1)}x_{n(t-1)}||^2$

$=||w_{t-1}||^2+2y_{n(t-1)}w_{t-1}^Tx_{n(t-1)}+||y_{n(t-1)}x_{n(t-1)}||^2$

$\leqslant ||w_{t-1}||^2+0+||y_{n(t-1)}x_{n(t-1)}||^2$

$\leqslant ||w_{t-1}||^2+\underset{n}{max}||x_{n}||^2$

$\leqslant ||w_{0}||^2+T*\underset{n}{max}||x_{n}||^2$

$=T*\underset{n}{max}||x_{n}||^2$

即： $||w_t||\leqslant \sqrt{T}*\underset{n}{max}||x_n||$

-----------------------------------------------------------------------------------

$1\geqslant cos\theta =\displaystyle \frac{w_f^T}{||w_f^T||}\frac{w_t}{||w_t||}\geqslant \frac{T*\underset{n}{min}\, y_nw_f^Tx_n}{||w_f^T||||w_t||}$

$\geqslant \frac{T*\underset{n}{min}\, y_nw_f^Tx_n}{||w_f^T||*\sqrt{T}*\underset{n}{max}||x_n||} = \frac{\sqrt{T}*\underset{n}{min}\, y_nw_f^Tx_n}{||w_f^T||*\underset{n}{max}||x_n||}=\sqrt{T}*constant$

即：随着 $T$ 的增加， $\sqrt{T}$ 不断增大， $cos\theta$ 的下限不断增加，在 $\left [ -\pi, \pi\right ]$ 区间（向量夹角不可能大于180）， $\theta$ 角度上限不断减小，总体来看角度变小（机器学习不确定因素大，没法保证每一步都比上一步角度小，参考上面2.2节图）。

3.4，修正次数上限

即： $\frac{w_f^T}{||w_f^T||}\frac{w_t}{||w_t||}\geqslant \frac{\sqrt{T}*\underset{n}{min}\, y_nw_f^Tx_n}{||w_f^T||*\underset{n}{max}||x_n||}=\sqrt{T}*constant$

因为 $\frac{w_f^T}{||w_f^T||}\frac{w_t}{||w_t||} \leqslant 1$ ，可得：

$\frac{\sqrt{T}*\underset{n}{min}\, y_nw_f^Tx_n}{||w_f^T||*\underset{n}{max}||x_n||}\leqslant 1$

即： $T\leqslant \frac{\underset{n}{max}||x_n||^2*||w_f^T||^2}{\underset{n}{min}^2\, y_nw_f^Tx_n}=\frac{R^2}{\rho ^2}$

3.4，线性不可分（Pocket PLA）

如果数据集是线性不可分的，那么对PLA进行改进，类似贪心算法：在pocket中保留一条当前最好的线，如果改进后的线更好（错分的样本数少），则更新最好的线，这样的缺点是需要遍历完空间内所有点的才能得到最好的结果。

对 $n$ 个样本进行遍历，遇到错误就更新 $w_t$ 为临时变量 $w_{t+1}$ 。如果 $w_{t+1}$ 的错误个数比 $w_t$ 的错误个数少的话，就更新 $w_t$ 为 $w_{t+1}$ ，否则不进行更新。