机器学习:决策树(一) ——自己动手实现决策树和后剪枝
一、决策树(Decision Tree)介绍什么是决策树,其实字面意思挺简单的,就是通过样本的各个维度的数据来判断该样本的类别,比如下面这个就是决策树。图片来自周志华老师的西瓜书,这里的决策树通过西瓜的各个属性来判别是好瓜还是坏瓜。现在的任务就是构建这样一棵决策树:(一)应该先以哪个属性做判别?(找到令数据集区分的更好的属性)...
一、决策树(Decision Tree)介绍
什么是决策树,其实字面意思挺简单的,就是通过样本的各个维度的数据来判断该样本的类别,比如下面这个就是决策树。
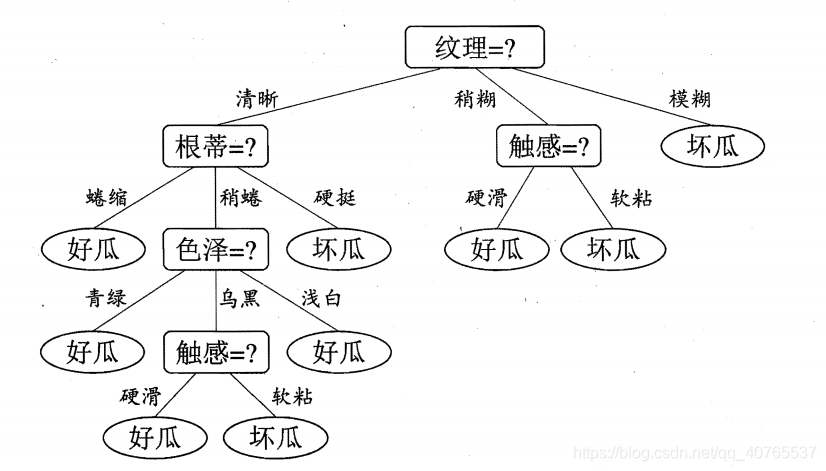
图片来自周志华老师的西瓜书,这里的决策树通过西瓜的各个属性来判别是好瓜还是坏瓜。
现在的任务就是构建这样一棵决策树:
(一)应该先以哪个属性做判别?(找到令数据集区分的更好的属性)
(二)是不是每条路径都以所有属性做支撑?(剪枝问题)
(一)、找到最好的特征(或称属性),共有三种算法
1. ID3算法(ID意思是 Iterative dichotomiser, 迭代二分器)
一般而言,随着划分过程不断进行,我们希望决策树的分支样本尽可能属于同一类别,即节点的“纯度”(purity)越来越高。
在ID3算法中我们使用信息熵(information entropy)衡量纯度(定义如下),熵越小,纯度越高(记得高中时有学过熵增定理,道理一样的)。
其中,D是样本集,是第k类占比,共有K类 。
ID3算法是以信息增益(information gain)来选择最好的特征的,下面的式子是以属性a作划分的信息增益。
其中,v代表value,指数据集中属性a的取值,我们把不同取值的数据分开,分别计算它们的信息熵,加总即可得到以属性a划分后的信息熵。信息增益对应到决策树上就是父节点信息熵和它的各个子节点信息熵之和的差值。
ID3选择的是信息增益最大的属性。
ID3算法的缺点:
信息增益对可取值数目较多的属性有所偏好,想象一下,假设一个属性的取值数目跟样本数量一样,即每个取值只有一个样本,这个时候就是
,此时该属性的信息增益当然是最大的。
2. C4.5算法
ID3和C4.5都是由Quinlan提出的算法,C4.5可以看作是ID3的升级版,它用来规避ID3算法偏好可取值数目较多的属性的缺点。
方法就是通过信息增益率来选择最佳属性,其定义如下:
我们可以来对比一下IV(a)和Entropy(D),事实上他们的计算方式是一样的,Entropy(D)是数据集D的标签列label的信息熵,我们希望纯度高,label信息熵小,IV(a)是数据集D的属性列a的信息熵,我们希望a的取值数少一些,也就是纯度高,a信息熵小。
C4.5算法的目标是选择信息增益高于平均水平,且信息增益率最大的属性。
C4.5的优点:
规避了ID3算法偏好可取值数目较多的属性的缺点。
C4.5的缺点:
增益率对于可取值数目少的属性有所偏好,一般是先从获选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3. CART算法[Breiman et al.,1984] (Classification And Regression Tree)
CART算法采用基尼值来衡量数据集纯度,定义如下:
基尼值反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,基尼值越小,数据集D的纯度越高。
属性a的基尼指数定义为:
C4.5算法选择的是基尼指数最小的属性。
4. 决策树的共有优缺点:
1)优点:
有一定的抗噪能力,因为ID3使用的是所有样例的统计属性(比如,信息增益),这大大降低了对个别错误的训练样例的敏感性。
2)缺点:
A.当遍历决策树空间时,ID3仅维护单一的当前假设。失去了表示所有一致假设所带来的优势,例如,它不能判断有多少个其他的决策树也是与现在的训练数据是一致的。
B.基本的ID3算法在搜索中不进行回溯。每当在树的某一层次选择了一个属性进行测试,它不会再回溯重新考虑这个选择。所以,它易受无回溯的爬山搜索中的常见风险影响:收敛到局部最优的答案,而不是全局最优的。对于ID3算法,一个局部最优的答案对应着它在一条搜索路径上探索时选择的决策树。然而,这个局部最优的答案可能不如沿着另一条分支搜索到的更令人满意。后面我们讨论一个扩展,增加一种形式的回溯(后修剪决策树)。
C.较短的树比较长的树优先。那些信息增益(增益率,基尼指数)高的属性更靠近根结点的树优先。
(二)、剪枝方法
剪枝主要用来解决过拟合的问题,因为分支太多,太深了,模型的泛化能力就会下降。
1.预剪枝(prepruning)
(1)当信息增益或者信息增益率小于某个阈值的时候,停止划分。
(2)留出法:把数据划分成训练集和验证集,在要划分的时候看该划分能否使模型在验证集的精度度提升,若是,则划分,若否,则停止划分。
缺点:
预剪枝基于“贪心”思想禁止分支展开,决策树会有欠拟合的风险。
2.后剪枝(postpruning)
对决策树进行深度优先搜索,对于能使验证集精度提高的剪枝,进行剪枝,否则保留分支。
优点:
一般情形下,后剪枝决策树的欠拟合风险很小,泛化能力由于预剪枝
缺点:
后剪枝过程是在生成完全决策树之后进行的,并且要子弟向上的对书中所有的非叶子节点进行注意考察,因此其训练的时间开销比未剪枝决策树和预剪枝决策树要大得多。
二、代码实现
(一)创建树的过程
import numpy as np
#%%
class Tree(object):
def __init__(self,node_type,category=None,feature=None,\
feature_idx=None,mydict=None):
self.node_type = node_type # 节点类型
self.category = category # 叶子节点表示的类,若是内部节点则为空
self.feature = feature # 表示当前的树由第feature个特征进行划分
if not mydict:
self.mydict = {}
else:
self.mydict = mydict # 字典
def add_subtree(self, key, subtree):
self.mydict[key] = subtree
def predict(self, x):
# print("[DEGUB]:%s"%(x))
if self.node_type == 'LEAF'\
or x[self.feature] not in self.mydict:
return self.category
tree = self.mydict.get(x[self.feature])
return tree.predict(x)
def cal_entropy(x):
x_value_list = set(x)
entropy = 0.0
for x_value in x_value_list:
prob = float(x[x == x_value].shape[0]) / x.shape[0]
entropy -= prob * np.log2(prob)
return entropy
# 计算条件熵H(label/attr)
def cal_conditional_entropy(attr, label):
attr_values = set(np.squeeze(attr))
entropy = 0.0
for value in attr_values:
sub_label = label[attr == value]
sub_entropy = cal_entropy(sub_label)
entropy += (float(len(sub_label))/len(label))*sub_entropy
return entropy
def create_tree(data, label, features):
# 1.如果训练集中所有数据均属于同一类,即可返回
label_set = set(label)
if len(label_set) == 1:
category = label_set.pop()
subtree = Tree('LEAF', category=category)
print("[INFO]: create a leaf node, category is %s"%(category))
return subtree
# 2.如果特征集为空
label_set = set(label)
max_class = label[0]
max_num = 0
for each in label_set:
class_num = label[label==each].shape[0]
if class_num > max_num:
max_class = each
max_num = class_num
if len(features) == 0:
subtree = Tree('LEAF', category=max_class)
print("[INFO]: create a leaf node, category is %s"%(max_class))
return subtree
# 3.找到信息增益最大的特征
base_entropy = cal_entropy(label)
best_feature = features[0]
max_info_gain = 0
for i in features:
attr = data[:,i]
info_gain = base_entropy - cal_conditional_entropy(attr, label)
if info_gain > max_info_gain:
best_feature = i
max_info_gain = info_gain
# 4.如果信息增益小于阈值,进行预剪枝
if max_info_gain < 0.001:
return Tree('LEAF', category=max_class)
# 5.构建内部节点以及递归创造子树
sub_features = list(filter(lambda x: x != best_feature, features))
tree = Tree('INTERNAL', feature=best_feature, category=max_class)
print("[INFO]: create a internal node,feature is %sth"%(best_feature))
best_feature_values = set(data[:, best_feature])
for value in best_feature_values:
indexs = data[:, best_feature] == value
sub_data = data[indexs]
sub_label = label[indexs]
sub_tree = create_tree(sub_data, sub_label, sub_features)
tree.add_subtree(value, sub_tree)
return tree
def predict(test_data, tree):
result = []
for each in test_data:
result.append(tree.predict(each))
return np.array(result)(二)后剪枝代码的实现
def post_pruning(val_data, val_label, dataset, tree, features):
path = []
DFS.val_data = val_data
DFS.val_label = val_label
DFS.dataset = dataset
DFS.root = tree
DFS.features = features
DFS(tree, path)
return tree
def DFS(tree, path):
if tree.node_type == "LEAF":
print("[INFO]:post pruning, arrive at leaf node")
return
# 没有return,该节点是内部节点,检测该节点的子节点是不是都是叶子节点
leafs_parent = True
for sub_tree in tree.mydict.values():
if sub_tree.node_type != "LEAF":
leafs_parent = False
break
# 如果该节点的子节点全部是叶子节点
if leafs_parent and len(path) > 0:
process_leafs_parent(DFS.val_data,DFS.val_label,
DFS.dataset, DFS.root, DFS.features,tree, path)
# 如果该节点的子节点也是内部节点,继续递归
else:
for key, sub_tree in tree.mydict.items():
path.append((DFS.features[tree.feature], key))
DFS(sub_tree, path)
path.pop()
# 对子节点的递归结束,
# 再次检测该节点的子节点是不是都是叶子节点
leafs_parent = True
for sub_tree in tree.mydict.values():
if sub_tree.node_type != "LEAF":
leafs_parent = False
break
# 如果该节点的子节点全部是叶子节点
if leafs_parent and len(path) > 0:
process_leafs_parent(DFS.val_data,DFS.val_label,
DFS.dataset, DFS.root, DFS.features, tree, path)
def process_leafs_parent(val_data,val_label,
dataset, root, features, tree, path):
# 在未剪枝的决策树上进行验证,并得出f1
old_score = f1_score(val_label, predict(val_data, root),average='micro')
# 将未剪枝的子树保存起来
temp_tree = copy.deepcopy(tree)
# 根据路径找到训练集中能到达该节点的数据
df = pd.DataFrame(dataset, columns=features+['label'])
query = str(path[0][0])+"=="+str(path[0][1])
if len(path) >= 2:
for each in path[1:]:
query += " and "+str(each[0])+"=="+str(each[1])
print(query)
df = df.query(query)
# 进行剪枝
tree.category = Counter(df.iloc[:, -1]).most_common(1)[0][0]
tree.node_type = "LEAF"
tree.mydict = {}
# 若剪枝后分数变低,那么还原子树
new_score = f1_score(val_label, predict(val_data, root),average='micro')
if(new_score < old_score):
tree.category = temp_tree.category
tree.node_type = temp_tree.node_type
tree.mydict = temp_tree.mydict(三)使用
这里使用iris数据集进行测试
from sklearn.datasets import load_iris
from tree_plotter.tree_plotter import create_plot
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
data = load_iris()
x = data['data']
y = data['target']
data_train, data_val, label_train, label_val = train_test_split(x,y,test_size=0.2)
mytree = create_tree(data_train, label_train,[0,1,2,3])
create_plot(mytree)
post_pruning(data_val, label_val, np.c_[data_train, label_train], mytree,['a','b','c','d'])
create_plot(mytree)
print(classification_report(label_val, predict(data_val, mytree)))输出:
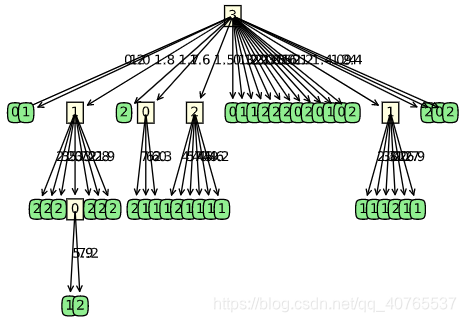
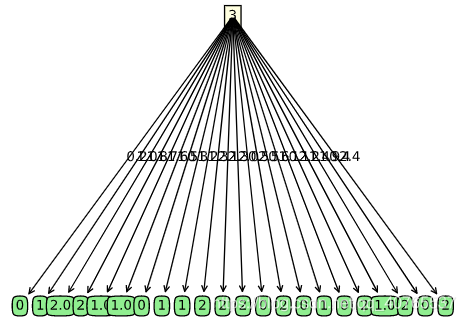
后剪枝之前 后剪枝之后
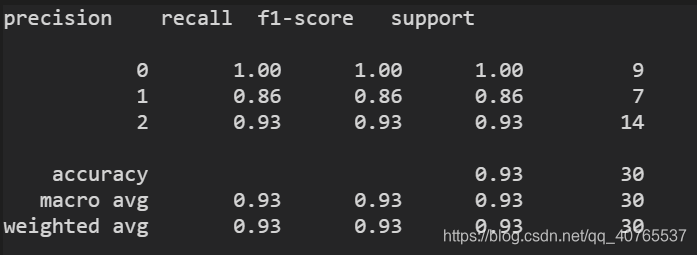
可以看到准确率有0.93。
关于树的可视化,可以参考下面的链接。
三、总结
1. 上述实现采用的是ID3算法,C4.5的实现在:戳这里
2. 对于连续型属性值,我们需要进行二值化,可以参考:机器学习:决策树(二) ——对于连续值的二值化处理
3. 对于决策树,我们可以进行可视化,可以参考:机器学习:决策树(三)——决策树的可视化
4. 对应平时使用来讲,我们不用自己实现代码,可以直接调用skearn中已经实现好的决策树,详情请看:
机器学习:决策树(四)——sklearn决策树的使用及其可视化
四、参考文献
【1】《机器学习实战》Peter+Harrington
【2】《机器学习》周志华
文章为学习总结,如果错误的地方,欢迎指出。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容








所有评论(0)