北京大学 葛钤

 

编者按：

原文《Realtime Top-k Personalized Pagerank over Large Graphs on GPUs》介绍了一篇在GPU对大规模图上进行个性化pagerank计算的论文。本篇论文的主要结构是先介绍了问题定义和已有的基于CPU的算法，并在此基础上完成了在GPU上的优化和改进。主要包括：

• 提出了在GPU上更适合的数据存储结构。

• 进行了适应性的前向随机游走。

• 并行地实现预处理和候选集的更新。

 

论文地址：

http://www.vldb.org/pvldb/vol13/p15-shi.pdf

（或点击文末“阅读原文”跳转）

 

 

1 Problem Definition

 

 

 

(1) Personalized PageRank：

给定一个有向图G=（V,E），其中V和E分别是图的点集和边集，顶点数目为n，边数目为m，给定一个源点u以及一个停止概率α。从u出发的随机游走定义如下：每一步有α的概率停止，或者等概率跳到当前节点的每个出邻居。对于每个节点v，从u到v的个性化PageRank值π(s, v)定义为从s出发的随机游走到v点停止的概率。对于无向图，类似地可以将每条边视为两个方向的边一起构成。

 

（2）Approximate Top-k PPR Queries

Top-k 单源PPR是指从源点出发，到所有点的PPR中最大的k个，但是由于PPR本身难以精确计算，通常都采用上述的近似定义，即给定误差范围和阈值以及失败概率，（1）式保证当PPR真实值大于阈值时，始终有估计值和真实值的差在相对误差界内，（2）式保证了返回的点的值与真实的top-k的误差在限度内。

 

2 Existing CPU-based Methods

 

 

 

（1）Monte-Carlo：

从源点s出发，引出足够数量的随机游走，其中停在v点的比例就是s到v的ppr的无偏估计，经过足够多的采样就能够通过概率不等式保证误差在一定限度内。

 

（2）Forward-Push：

如上述伪码所示，设置残差r，一开始s点残差为1，其余为0；之后当节点满足第9行的条件时，就放进待push的集合中，并不断地向外push。注意到开始时总残差之和r为1，每进行一次push，r都至少减少α*rmax，因此理论复杂度为O(1/rmax)。

 

（3）FORA：

是将forward-push与Monte-Carlo方法相结合，先从起点s开始进行forward-push，当满足残差都小于一个阈值时，开始从剩余的点进行随机游走，并且利用下式进行估计，注意到用随机游走的部分会乘以当前残差，因此会减少总的误差，并通过设置阈值和随机游走数目来达到较精确的估计。

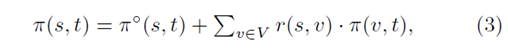
（4）TopPPR：

是由forward-push和backward-push以及Monte-Carlo方法相结合，利用下式进行估计，本质上类似于将(3)式再展开了一层。

 

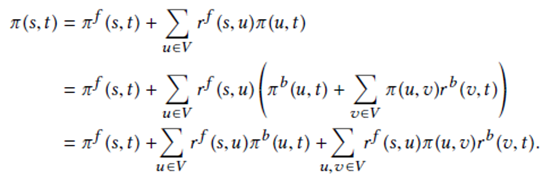
3 Algorithm

 

 

 

(1)Adaptive Forward Push

 伪码如上，与之前的Forward-Push十分相似，本质上是通过为每个点u来设置不同的残差阈值rmax(u)，类似地用frontier来表示r(s,u)/dout(u)大于rmax(u)的点。

如果照搬Forward-Push的做法，会导致frontier集合数目起初减少很快，后续减少得越来越慢，最末尾的大部分迭代，可能只有极少数的frontier来参与，这也就意味着表示其他点的线程出现了空闲浪费。因此文中的解决方法就是对于容易成为frontier的点设置更大的rmax，来避免一些后续不需要的迭代。

个性化rmax的思路是通过一种启发式的方法：文中认为一个节点是否容易成为frontier与pagerank（度量了每个点对于整个图的影响大小）有关，其中pagerank大的点可能更加容易聚集residue。因此预先计算出每个点的pagerank，按照pagerank/dout从大到小存储在PRO-rank list中。

具体的rmax设置如下图所示，其中β(u)与从u引出的随机游走的数目正相关，因为push的层数较少，因此需要更多的随机游走来保证其精确度。

（2）Inverted Random Walks

算法本身会涉及到从多个点出发引出随机游走，但是如果采用较常用的按照源点记录的方法，如果从u出发到达v的随机游走有多条，那么就会出现重复存储的情况。

为了更好地适应GPU的环境和避免重复记录，文中设计了下图所示的两层CSR结构的存储：

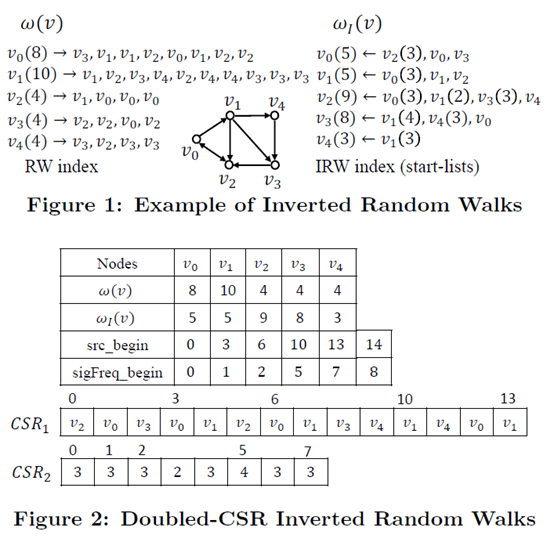
其中下标为v的IRW存储了以v作为终点的随机游走的信息，表格中五行自上而下依次表示节点名，节点作为起点的随机游走数，节点作为终点的随机游走数，在csr1中的下标，在csr2中的下标（这里只存储大于1的那些）

 

（3）Offline Indexing and Deciding rmax(v)

这一部分的思路是从每个点引出一定数目的随机游走来作为index存储在IRW结构中，并根据之前的Pro-rank list确定每个点的随机游走数目。

具体做法是：先从每个点引出w(v)条随机游走。考虑存储空间的限制，假设还有W的空余空间，按照Pro-rank list从大到小的顺序，预设a为2的幂次，每个点额外走(a-1)*w(v)的随机游走，直到消耗了当前剩余空间的一半，此时将a减半，再继续下去。当a为2时，耗尽所有预算。最后根据每个点a的大小按下图所示来计算β(v)和rmax(v)。

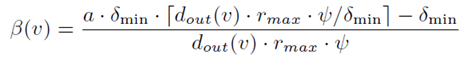
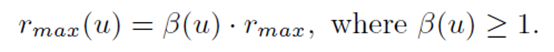
（4）Parallel Top-k PPR Processing

 

整个算法主体的伪代码如上所示，其中6-26行通过不断减少δ来尝试避免更多的随机游走，直接筛选出top-k的点，而27-31行则是在无法筛出后，后续用随机游走来算出更精确的PPR值，返回最大的k个。

 

（5）Parallel Candidate Set Generation

在进行候选集更新时，可以通过并行来减少时间复杂度。对应上图伪码第8行，在进行完ParallelAFP之后，即每个点的r(s,u)/dout(u)不大于rmax(u)后，每个点对应地有一个ppr估计值π(s,u)，这里是初步筛选，把估计值不小于δ的点留下。具体做法有两种：

设置flag，对于每一个点，在AFP过程中大于δ就标记1，最后再遍历统计所有大于1的点。或者维护一个Candidate数组，一旦大于δ就放进数组里，维护一个下标。

实际应用时，当候选集数目较小时，采用第二种做法，否则采用第一种。

 

（6）Set PPR Bounds

结合前面推导得出，当AFP进行完之后，对于任意点u，从任一点出发的随机游走在u停止对于u点ppr影响不超过ρ，其中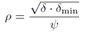 

因此给出每个点ppr的上界π ̂^ub：

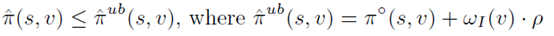
而对于所有不属于候选集的点，ppr上界为 

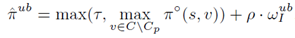
其中 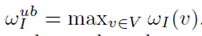而对于在目前top-k集合中的点v，上下界表示如下：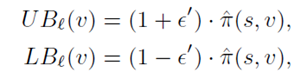

（7）Bound Reduction in Parallel

仍然存在这样的问题：w_I (v)可能会很大，导致上下界不够紧。文中的解决方法是将w_I (v)很大的点v摘出来，单独进行更精确的估计（见下图算法）。

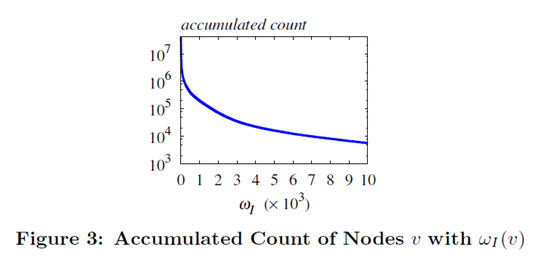
且根据经验得知点的的数目与w_I (v)的分布如下图所示，因此这样的点不会很多。

（8）Complexities

其中forward-push和随机游走所需的时间和空间复杂度如下图所示：

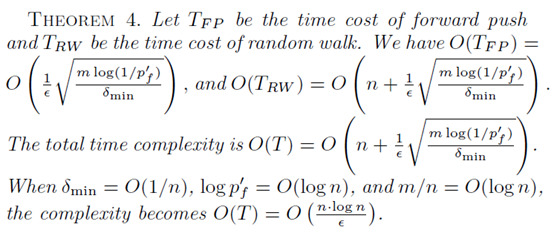
而其中用到的数据结构的空间复杂度分析如下：

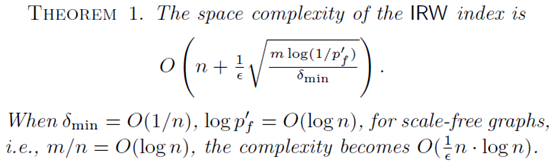
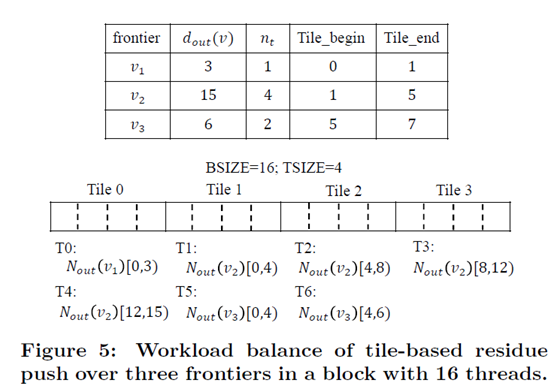
（9）Parallel Optimizations

对于线程按照每个点的出度进行了合适的分配，按照每个Tile完成相应一部分邻居的工作。

 

4 Experiment

 

 

 

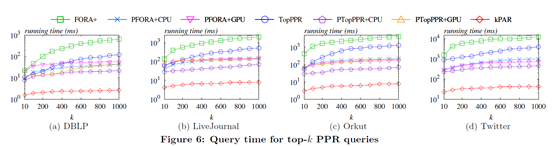
（1）Query time：

文中将提出的算法（kPAR）与常见的top-k ppr的算法FORA，TopPPR等进行了对比，可以看出kPAR在查询速度上有着非常明显的提升

（2）Query Accuracy

在查询的精确度上有两种设置，分别是Precision：比较了返回的点集中的点在实际top-k点集中的占比。和Normalized Discounted Cumulative Gain（NDCG）：计算方法如下，进一步对于顺序的正确性进行区分。

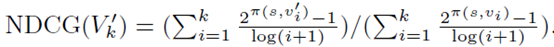
在这样的两个精度标准下，将文中的kPAR算法与其他算法进行比较，结果如下： 

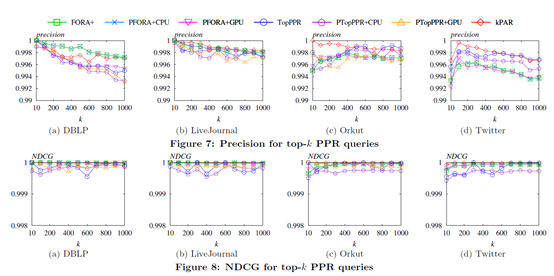
可以看出，文中提出的kPAR算法始终有着很高的精确度。

（3）Preprocessing Time and Space Overhead

在预处理时间和总的存储开销上来看，由于kPAR为了更好地减少online算法的时间，选取了一部分点进行更多随机游走，但是整整体上与FORA+算法的开销相近。

 

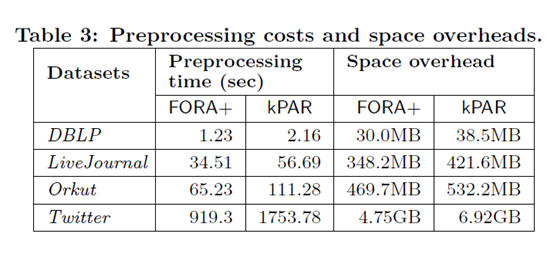
5 总结

 

 

 

本文介绍了如何在GPU上解决大规模图上的单源top-kPPR查询问题，是对CPU上的FORA算法进行的一系列调整与改进，使得算法能够更好地契合GPU的性质，最终在保证高精确度的同时，对于时间复杂度有着数量级的缩减。对于后续PPR的研究以及在GPU上进行拓展有着很强的参考意义和启发价值。