八自由度 四足机器人运动学正解及逆解(附代码)
已知两个关节的角度(θ₁和θ₂),求脚底的位置坐标(x, y)。
·
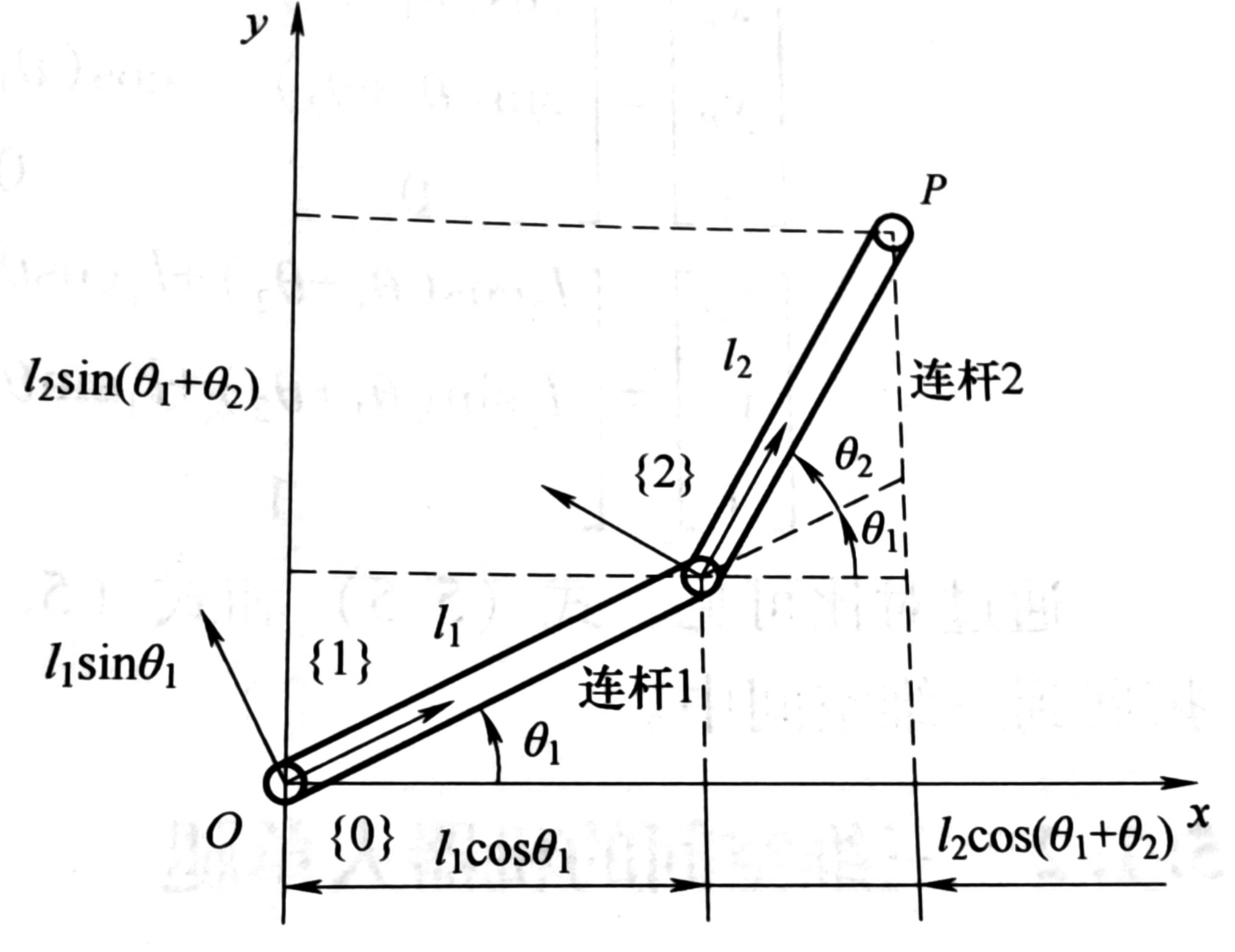
一.运动学正解
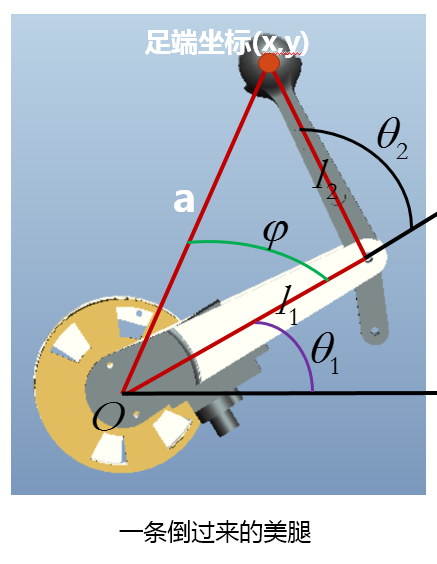
-
已知两个关节的角度(
和
),以及连杆长度,求足端的位置坐标
。
步骤分解:
-
建立坐标系:以髋关节为原点,向上为
轴正方向,向右为
轴正方向。
-
-
大腿的位置:
-
大腿长度为
,髋关节角度为
从
轴向下旋转为正)。
-
大腿末端(膝关节)的坐标:
-
-
小腿的位置:
-
小腿长度为
,膝关节角度为
(相对于大腿的旋转角度)。
-
脚底的坐标(相对于膝关节):
-
-
-
脚底总坐标:
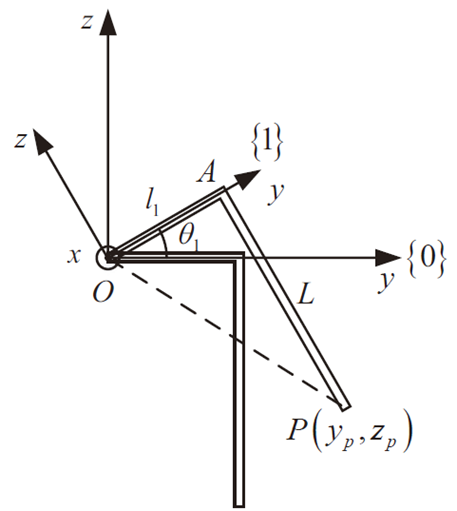
-
正解就是“已知关节角度,算脚的位置”,就像知道你的大腿和小腿弯了多少度,计算脚能伸到哪里。
二、逆运动学(Inverse Kinematics)
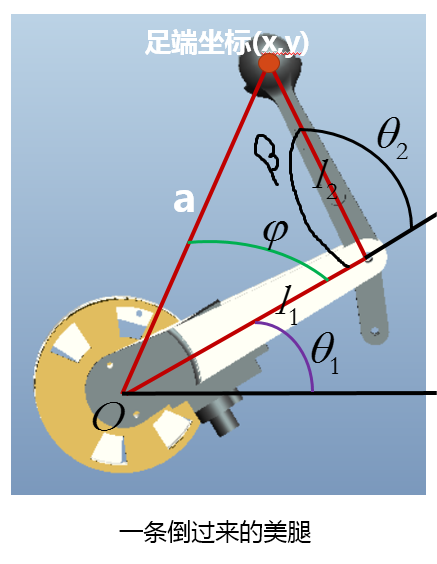
-
问题:已知脚底的目标位置(x, y),求两个关节的角度(θ₁和θ₂)。
步骤分解:
-
勾股定理:计算从髋关节到脚底的距离:
-
设x,y坐标已知,从足端坐标作垂线,根据勾股定理可得:
或者
-
如果
或
,则目标位置不可达(正解已对关节角度进行限制,所以不用考虑超出机器人角度范围)。
-
-
-
2.1 余弦定理:求膝关节角度 θ₂:
-
 ,列式可得:
,列式可得: - 将
代入式:
-
- 移项解出:
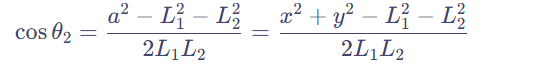
- 最后求出:
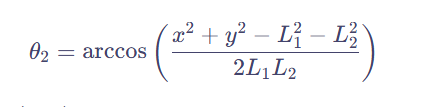
-
2.2 求髋关节角度 θ1:
-
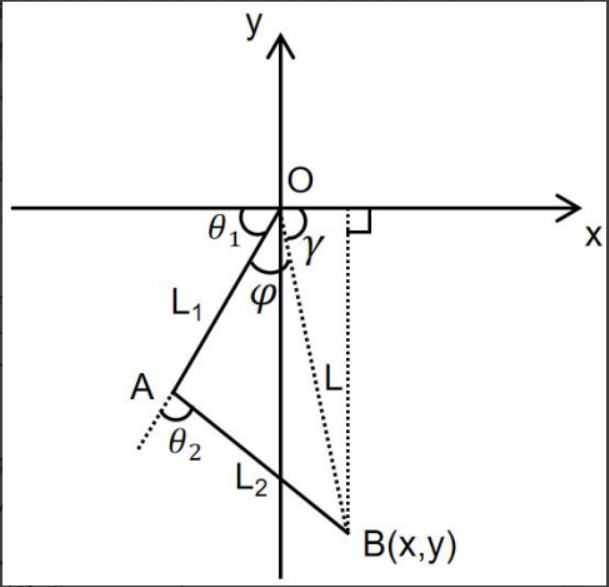
- 余弦定理,已知三角形的三条边长,可以使用反余弦函数求解三角形中某个角。
-
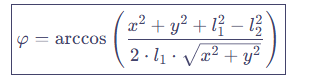
- 反正切求得:
- 当x>0时:

- 当x<0时:
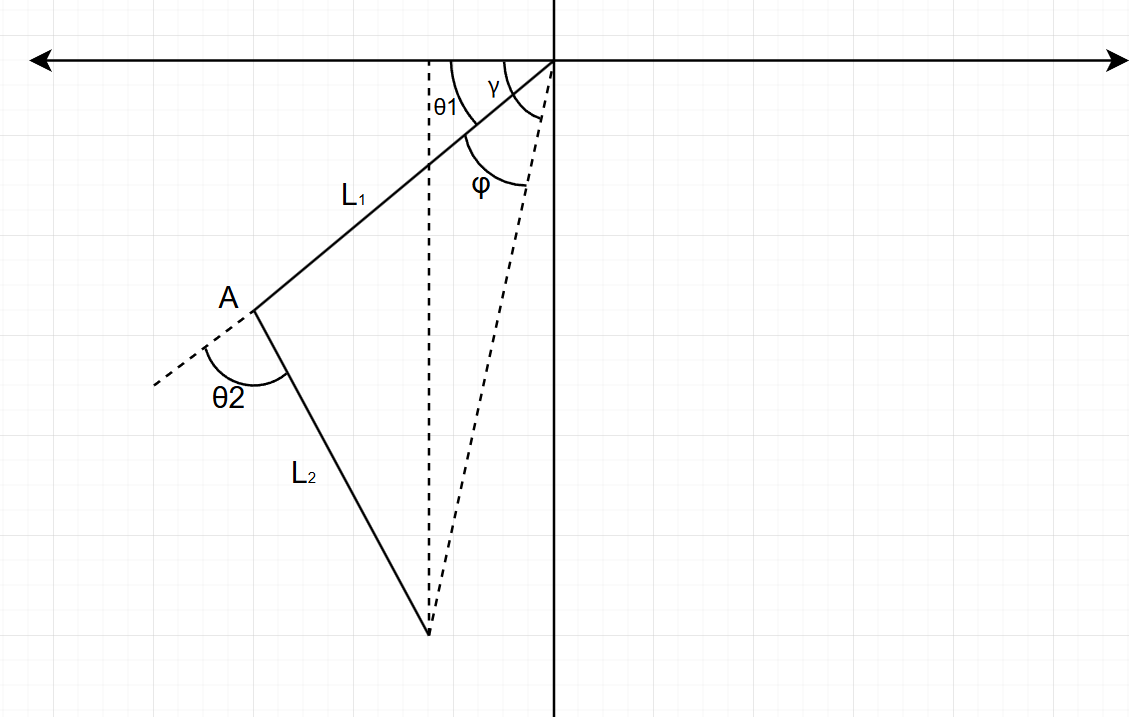
- 当x=0时:
(自己画图理解下~)
三、代码实现
3.1 运动学逆解
/*默认速度 步长 设置*/
float l1 = 200; //大腿长(mm)
float l2 = 160; //小腿长(mm)
float h = 30; //抬腿高度 设置
float xf = 40; //xf为终点足端坐标
float xs = -20; // xs起始足端坐标
float Ts = 1; //周期
float faai = 0.5; //占空比
float speed = 0.025; //步频调节
//=============一些中间变量=============
float t = 0;//时间变量
float init_x = 0;
float init_y = -290;//腿高度
float x1 = init_x;//腿1x坐标
float y1 = init_y;//腿1y坐标
float x2 = init_x;
float y2 = init_y;
float x3 = init_x;
float y3 = init_y;
float x4 = init_x;
float y4 = init_y;
float ges_x_1 = 0;
float ges_x_2 = 0;
float ges_x_3 = 0;
float ges_x_4 = 0;
float ges_y_1 = init_y;
float ges_y_2 = init_y;
float ges_y_3 = init_y;
float ges_y_4 = init_y;
void calculateLegAngles(float x, float y, float* hip_angle, float* knee_angle) {
x = -x;
*knee_angle = pi - acos((x * x + y * y - l1 * l1 - l2 * l2) / (-2 * l1 * l2));
float fai = acos((l1 * l1 + x * x + y * y - l2 * l2) / (2 * l1 * sqrt(x * x + y * y)));
if (x > 0) {
*hip_angle = abs(atan(y / x)) - fai;
} else if (x < 0) {
*hip_angle = pi - abs(atan(y / x)) - fai;
} else {
*hip_angle = pi - 1.5707 - fai;
}
*knee_angle = 180 * *knee_angle / pi;
*hip_angle = 180 * *hip_angle / pi;
}
void IK(float x1, float y1, float x2, float y2, float x3, float y3, float x4, float y4) {
float hip_angle1, knee_angle1;
float hip_angle2, knee_angle2;
float hip_angle3, knee_angle3;
float hip_angle4, knee_angle4;
calculateLegAngles(x1, y1, &hip_angle1, &knee_angle1);
calculateLegAngles(x2, y2, &hip_angle2, &knee_angle2);
calculateLegAngles(x3, y3, &hip_angle3, &knee_angle3);
calculateLegAngles(x4, y4, &hip_angle4, &knee_angle4);
angle_output(hip_angle1, knee_angle1, hip_angle2, knee_angle2,
hip_angle3, knee_angle3, hip_angle4, knee_angle4);
}3.2 MATLAB可视化
% 设置参数
L = 200; % 腿的长度
Ls =160; %小腿长度
Tmax = 100; % 动画帧数
theta_range = linspace(0, 2*pi,Tmax); % 角度范围
theta_s_range= linspace(0, 2*pi,Tmax); % 角度范围
Ts=2;
fai=0.5;
% xs=-35;
% xf=65;
xs2=40;
xf2=-10;
h=50;
zs=-290;
% 创建图形窗口
figure;
set(gcf, 'Position', [100, 100, 1000, 800]); % 增大窗口尺寸以便显示更多信息
for t= 0:0.04:5
t_mod = mod(t, 1); % 取模,使 t 在 0 到 1 之间循环
if t_mod<Ts*fai
sigma=2*pi*t_mod/fai/Ts;
zep2=h*(1-cos(sigma))/2+zs;
xep3=(xf2-xs2)*(sigma-sin(sigma))/(2*pi)+xs2;
xep4=(xs2-xf2)*(sigma-sin(sigma))/(2*pi)+xf2;
y3=zep2;
y4=zs;
end
if t_mod>Ts*fai && t_mod<Ts
sigma=2*pi*(t_mod-(Ts*fai))/fai/Ts;
zep2=h*(1-cos(sigma))/2+zs;
xep3=(xs2-xf2)*(sigma-sin(sigma))/(2*pi)+xf2;
xep4=(xf2-xs2)*(sigma-sin(sigma))/(2*pi)+xs2;
y3=zs;
y4=zep2;
end
%plot([0, xep], [0, y], 'bo-', 'LineWidth', 2)
%求φ角度
fail3= acos((xep3.^2 + y3.^2 + L.^2 - Ls.^2) /(2 *L*sqrt(xep3.^2+y3.^2)));
fail4= acos((xep4.^2 + y4.^2 + L.^2 - Ls.^2) /(2 *L*sqrt(xep4.^2+y4.^2)));
if xep3>0
sita3=abs(atan(y3/xep3))-fail3;
end
if xep3 <0
sita3=pi-abs(atan(y3/xep3))-fail3;
end
if xep3==0
sita3=pi-1.5707-fail3;
end
if xep4>0
sita4=abs(atan(y4/xep4))-fail4;
end
if xep4 <0
sita4=pi-abs(atan(y4/xep4))-fail4;
end
if xep4==0
sita4=pi-1.5707-fail4;
end
%求θ2
knee_angle3 = acos((xep3.^2 + y3.^2 - L.^2 - Ls.^2) /(2 *L*Ls));
knee_angle4 = acos((xep4.^2 + y4.^2 - L.^2 - Ls.^2) /(2 *L*Ls));
Lx3=L*cos(sita3);
Ly3=L*sin(-sita3);
Lx4=L*cos(sita4);
Ly4=L*sin(-sita4);
clf; % 清空当前图形
hold on;
plot([0, Lx3], [0, Ly3], 'bo-', 'LineWidth', 20)
plot([Lx3,xep3],[Ly3,y3],'ro-','LineWidth',15);
plot([0, Lx4], [0, Ly4], 'bo-', 'LineWidth', 20)
plot([Lx4,xep4],[Ly4,y4],'ro-','LineWidth',15);
center3=[xep3,y3];
center4=[xep4,y4];
viscircles(center3, 40, 'Color', 'g', 'LineWidth', 2);
viscircles(center4, 40, 'Color', 'g', 'LineWidth', 2);
% ================ 新增内容:显示角度和坐标信息 ================
% 转换角度为度数
sita3_deg = rad2deg(sita3);
sita4_deg = rad2deg(sita4);
fail3_deg = rad2deg(knee_angle3);
fail4_deg = rad2deg(knee_angle4);
% 在关节位置显示角度信息
text(0, -20, sprintf('大腿角度: %.1f°', sita3_deg), 'Color', 'b', 'FontSize', 12);
text(0, -40, sprintf('大腿角度: %.1f°', sita4_deg), 'Color', 'b', 'FontSize', 12);
text(Lx3, Ly3+30, sprintf('小腿角度: %.1f°', fail3_deg), 'Color', 'r', 'FontSize', 12);
text(Lx4, Ly4+30, sprintf('小腿角度: %.1f°', fail4_deg), 'Color', 'r', 'FontSize', 12);
% 在足端显示坐标信息
text(center3(1)+20, center3(2)+20, sprintf('足端: (%.1f, %.1f)', center3(1), center3(2)), 'Color', 'k', 'FontSize', 12);
text(center4(1)+20, center4(2)+20, sprintf('足端: (%.1f, %.1f)', center4(1), center4(2)), 'Color', 'k', 'FontSize', 12);
% 在顶部显示时间信息
text(50, 0, sprintf('时间: %.2f s', t), 'Color', 'm', 'FontSize', 14, 'FontWeight', 'bold');
% 添加图例说明
legend({'大腿', '小腿', '足端'}, 'Location', 'southeast');
% ========================================================
% 添加标签和标题
axis([-100, 300, -440, 20]);
xlabel('X轴');
ylabel('Z轴');
title('四足机器人腿部运动动画');
axis equal;
% 暂停一小段时间,以便观察动画效果
pause(0.01);
end
DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)