github地址

一、 实验目标：

  1. 了解各种数据类型在计算机中的表示方法
  2. 掌握C语言数据类型的位级表示及操作

二、实验环境：

  1. 计算机（Intel CPU）
  2. Linux操作系统

三、实验内容与步骤

  1. 根据bits.c中的要求补全以下的函数：
    int bitXor(int x, int y);
    int tmin(void);
    int isTmax(int x);
    int allOddBits(int x);
    int negate(int x);
    int isAsciiDigit(int x);
    int conditional(int x, int y, int z);
    int isLessOrEqual(int x, int y);
    int logicalNeg(int x);
    int howManyBits(int x);
    unsigned float_twice(unsigned uf);
    unsigned float_i2f(int x);
    int float_f2i(unsigned uf);
  2. 在Linux下测试以上函数是否正确，指令如下：
    *编译：./dlc bits.c
    *测试：make btest
    ./btest

四、实验结果

  1. int bitXor(int x, int y);
    思路：
    根据异或的定义：a^b = (a & ~b) | (~a & b)
    根据或的定义：a | b = (a & ~b)
    根据摩尔定律得到公式
int bitXor(int x, int y)
{
    return ~(~(x & ~y) & ~(y & ~x));
}
  1. int tmin(void);
    思路：
    根据补码的定义，最小二进制表示最高位为1，其他全0。
int tmin(void)
{
    return 1 << 31;
}
  1. int isTmax(int x);
    思路：
    根据补码的定义，最大二进制表示最高位为0，其他全1
    当x为最大二进制时，将其转化为全0。
    同时本题需要考虑特殊情况0xffffffff
int isTmax(int x)
{
   int i = x + 1;
   x = x + i;    
   x = ~x;       
   i = !i;     
   x = x + i; 
   return !x;
}
  1. int allOddBits(int x);
    思路：
    首先构造掩码temp=0xAAAAAAAA（偶数位为0，奇数位为1）
    将x的偶数为置0后，比较x与temp是否相等。
int allOddBits(int x)
{
    int temp = (170 << 24) + (170 << 16) + (170 << 8) + 170;
    x = x & temp;
    return !(x ^ temp);
}

5.int negate(int x);
思路：
根据补码的定义，负数为求反+1。

int negate(int x)
{
    return ~x + 1;
}
  1. int isAsciiDigit(int x);
    思路：
    如果x是Ascii，则48<= x <= 58
    对于x >= 48，判断x-48的标志位，如果为0说明为真，否则为假。
    对于x <= 58，判断x-59的标志位，如果为1说明为真，否则为假。
    （不选x-58是因为，当x=58时，x-58=0，标志位为0，与负数的标志位1不同，所以需要多减1）
    当二者同时为真时，返回真。
int isAsciiDigit(int x)
{
    return (!((x + (~0x30 + 1)) >> 31)) & ((x + (~0x3a + 1)) >> 31);
}
  1. int conditional(int x, int y, int z);
    思路：
    首先判断x是否为0：!x可以将所有x的取值统一成两个情况0或1。
    当x为0时，!x - 1 = 0xffffffff； 当x不为0时，!x - 1 = 0x00000000。
    如果要返回y，需要保留y，z置零。（因为0 | X = X，1&X=X，可以通过如果代码操作得到结果，这也是为何需要-1后将flag设为全1）。
    如果要返回z，同理。
int conditional(int x, int y, int z)
{
    int flag = !x + ~1 + 1;
    return (flag & y) | (~flag & z);
}
  1. int isLessOrEqual(int x, int y);
    思路：
    通过位运算实现比较两个数的大小
    两种情况：一是符号不同正数为大，二是符号相同看差值符号。
int isLessOrEqual(int x, int y)
{
    int y_minus_x = y+~x+1;          //y-x
    int Sign = y_minus_x >> 31 & 1; //y-x的符号
    int leftBit = 1 << 31;          //最大位为1的32位有符号数
    int x_sign = x & leftBit;       //x的符号
    int y_sign = y & leftBit;       //y的符号
    int bitXor = x_sign ^ y_sign;   //x和y符号相同标志位，相同为0不同为1
    bitXor = (bitXor >> 31) & 1;    //符号相同标志位格式化为0或1
    return ((!bitXor) & (!Sign)) | (bitXor & (x_sign >> 31));
}
  1. int logicalNeg(int x);
    思路：
    利用其补码的性质，除了0和最小数外其他数，标志位都是互为相反数关系。
    0和最小数的补码是本身，不过0的符号位与其补码符号位为0，最小数的为1，不影响。
    利用这一点得到解决方法。
    代码：
int logicalNeg(int x)
{
    return ((x | (~x + 1)) >> 31) + 1;
}
  1. int howManyBits(int x);
    思路：
    如果是一个正数，则需要找到它最高的一位（假设是n）是1的，再加上符号位，结果为n+1；如果是一个负数，则需要知道其最高的一位是0的。为了方便所以需要将负数取反。
    接着从高16位开始检查是否存在1，如果存在则说明至少需要16位，截断x，并检查下一部分。
    之后部分以此类推。
int howManyBits(int x)
{
    int b16, b8, b4, b2, b1, b0;
    int sign = x >> 31;
    x = (sign & ~x) | (~sign & x); 
//如果x为正则不变，否则按位取反（这样好找最高位为1的，原来是最高位为0的，这样也将符号位去掉了）
 
    b16 = !!(x >> 16) << 4; //高十六位是否有1
    x = x >> b16;           //如果有（至少需要16位），则将原数右移16位
    b8 = !!(x >> 8) << 3;   //剩余位高8位是否有1
    x = x >> b8;            //如果有（至少需要16+8=24位），则右移8位
    b4 = !!(x >> 4) << 2;   //同理
    x = x >> b4;
    b2 = !!(x >> 2) << 1;
    x = x >> b2;
    b1 = !!(x >> 1);
    x = x >> b1;
    b0 = x;
    return b16 + b8 + b4 + b2 + b1 + b0 + 1; //+1表示加上符号位
}
  1. unsigned float_twice(unsigned uf);
    思路：
    首先根据IEEE浮点数规则拆分uf。
    对于正数，尾数进行移位操作。
    对于负数，针对阶码进行相应操作。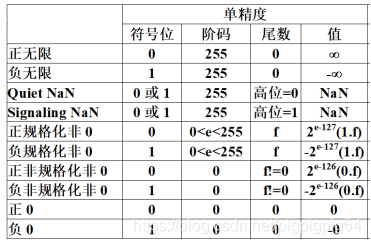
    在这里插入图片描述
unsigned float_twice(unsigned uf)
{
    // 提取各个字段
    unsigned s = uf & (0x80 << 24);
    unsigned exp = uf & ((0x7f << 24) + (0x80 << 16));
    unsigned frac = uf & ((0x7f << 16) + (0xff << 8) + 0xff);

    // 正数
    if (!exp)
    {
        frac = frac << 1;
    }
    // 负数
    else if (exp ^ ((0x7f << 24) + (0x80 << 16))) //如果阶码部分不为全1
    {
        exp += (0x80 << 16);          //阶码加1，对于规格化数，相当于乘2
        if (!(exp ^ ((0x7f << 24) + (0x80 << 16)))) 
//如果加1后，阶码为全1，将尾数位全置0，返回值即是无穷大
        {
            frac = 0;
        }
    }
    // exp == 255 返回原始值
    return s | exp | frac; //将符号位，阶码位，尾数位通过按位异或结合起来
}
  1. unsigned float_i2f(int x);
    思路：
    s是符号位(s=0或1)，M是尾数fraction，E的计算方式需要分类：
    规格化时(exp既不为全0也不为全1)，E = exponent - Bias，Bias是一个等于2^(k-1)+的偏置值，单精度是127。
    非规格化时(阶码域全0)，Exp = 1 -Bias。而非规格化时我们还能得到0和-0两个。
    首先把特殊情况0x0和0x80000000挑出来，因为移位是解决不了这两个的exp和frac。0x80000000时，exp为158，因为补码表示范围最大权重是，E最大取到31，而根据公式exp = E + Bias(127)，所以此时exp = 31 + 127 = 158。
    去掉两个特殊情况，当x为负数时，将其变成正数，便于后面的计算。
    令计数器为30，因为符号位不看，阶码域不为全1，则最高位不为1。依次减少右移位数，直到移动到第一个1处停下，此时 i 计为 Exp 的权重，可根据公式计算exp。
    将第一个1前的0左移去掉，因为31-23=8，int 转换为 float 要损失 8 位的精度，所以先把x 右移8位按位与 1 得到 frac，再来看最后8位是否要进位。
    原 x 进行掩码运算，只保留最后8位的有效数字，若超出128则进位，或者最高位是1，但是整体是奇数时也要向偶数进位，所以判断尾数是不是 1 。若进位则 frac + 1，如果frac 也突破23的限制了，那就给 E 加上1的权重，再把frac掩码运算一次。
    最后依次填空符号位阶码域小数域即可。
unsigned float_i2f(int x)
{
    int sign = x >> 31 & 1;
    int i;
    int exp;
    int frac;
    int delta;
    int mask;
    if (x == 0)
        return x;
    // x为最小整型数
    else if (x == 1 << 31)
        exp = 158;
    else
    {
        if (sign)
            x = -x;
        i = 30;
        while (!(x >> i))
            i--; //小数点偏移位数
        exp = i + 127;
        x = x << (31 - i);
        mask = 0x7f << 16 | 0xff << 8 | 0xff; // 0x7fffff
        frac = mask & (x >> 8);
        //得到23位的小数域

        x = x & 0xff;                                  //高8位
        delta = x > 128 || ((x == 128) && (frac & 1)); //向偶数舍入
        frac += delta;
        if (frac >> 23)
        {
            frac &= mask; //处理溢出情况
            exp += 1;
        }
    }
    return (sign << 31) | (exp << 23) | frac;
}
  1. int float_f2i(unsigned uf);
    思路：
    首先提取IEEE浮点数各个字段。
    对每一字段进行溢出判断并转化为对应的整型字段。
int float_f2i(unsigned uf)
{
    // 提取各个字段
    unsigned s = uf & (0x80 << 24);
    unsigned exp = (uf & ((0x7f << 24) + (0x80 << 16))) >> 23;
    unsigned frac = (uf & ((0x7f << 16) + (0xff << 8) + 0xff)) | (1 << 23);

    // 全为0，表示0，或者是小于1的非规格化浮点数，返回0
    if ((!exp) || exp < 127)
    {
        return 0;
    }
    // 溢出int的范围则返回1
    if (exp >= 31 + 127)
    {
        return 1 << 31;
}

    // 补码转化
    frac = frac >> (23 - (exp - 127));
    unsigned mask1 = (!s) + (~1) + 1;
    unsigned mask2 = ~(!s) + 1;
frac = (mask1 & ((~frac) + 1)) | (mask2 & frac);

    return s | frac;
}

五、实验总结与体会

最终结果展示：
在这里插入图片描述

Logo
DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

cover

KingbaseES数据库：医疗信创潮涌沅江，国产化信创打造医疗新质生产力

avatar DAMO开发者矩阵
cover

告别迁移焦虑：金仓KDMS V4带你轻松搞定数据库国产化替代

avatar DAMO开发者矩阵
cover

KingbaseES数据库在常德二院全栈国产化信创中产生新质生产力,医疗信创的部署如何实现，如何操作？

avatar DAMO开发者矩阵