这是个难题，不是我说的
会思路了。
要求的是最小的机器人的扫描范围，没别的，就是从小到大枚举扫描范围，然后用一个check函数，check函数需要用到左端点如果符合就输出步数
1.扫描范围：设置为Q。扫描范围是自己能到的最大的长度。例如上面的第一个机器人的扫描范围是4，第二个是3，第三个是3.
2.左端点：假设左端点左边的所有点都能被机器扫描到，L初始为0，从左到右增长，直到到区间最右边n。
3.check函数：用来判断当前的扫描范围能否把所有的点都扫描到

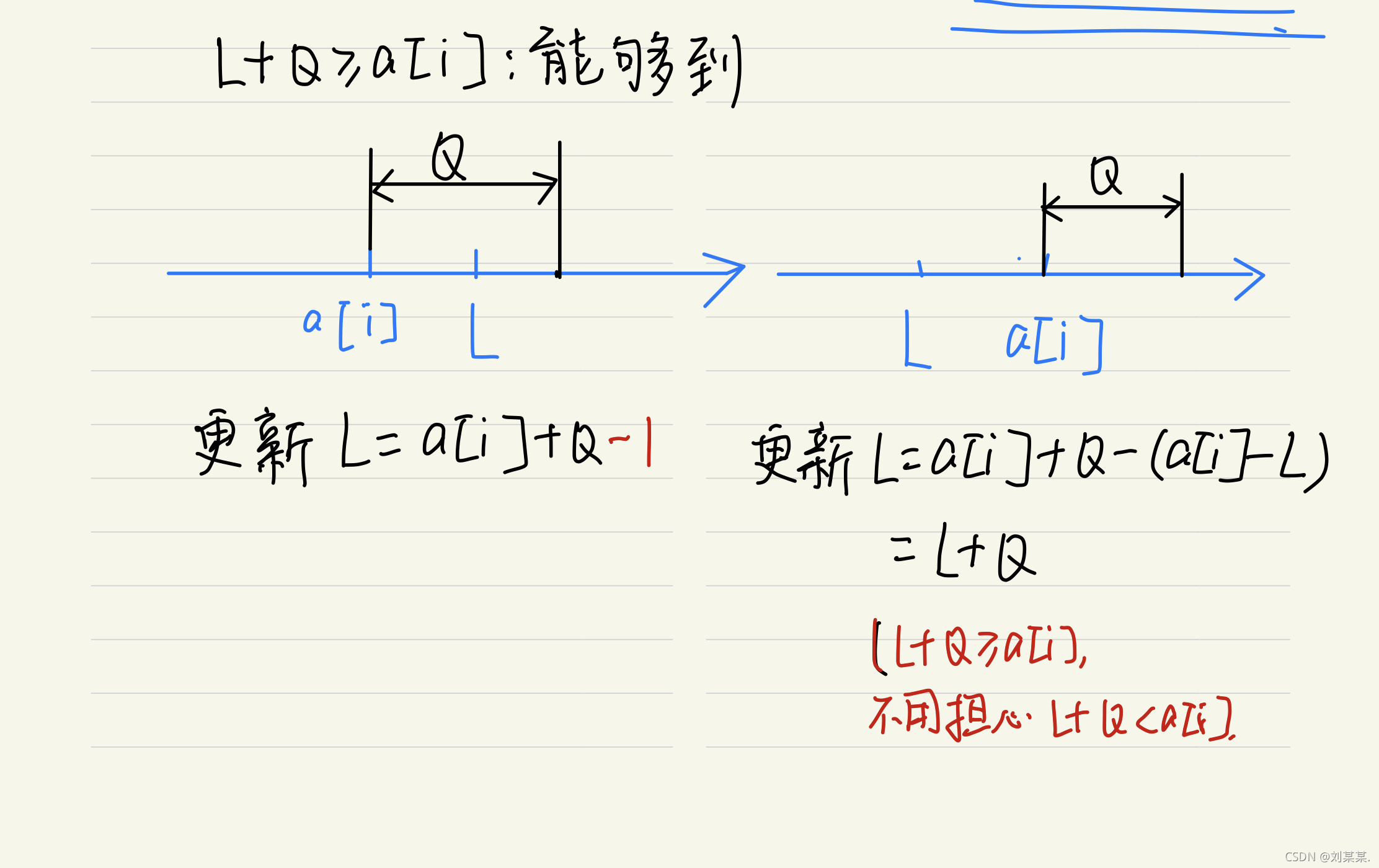
如果当前的L+Q <= a[i]的话，说明当前的左边界+区间长度都够不着 a[i]所在的位置，说明Q太小了直接return false；

如果L+Q>a[i]说明能够到，然后进去再判断：a[i]可能在L左边也可能在a[i]右边

如果a[i]在L左边，说明a[i]不需要扫描a[i]左边，只扫描a[i]右边就够了。更新L=a[i]+Q - 1，//Q是总区间长度，包括a[i]本身，所以要减去a[i]这个点。
.
如果a[i]在L右边，说明a[i]既需要能够到L，还要尽可能向右够到最远，更新L = a[i] + Q - (a[i] - L )，即L + Q从L直接加Q，一个道理。

4.步数：这个其实是和扫描范围区间长度有关系的，扫描范围是包括a[i]点本身能到的最大的长度，三个点1，2，3，从1走到3需要2步，再走回来仍需2步，区间长度假设为Q，则步数z= 2*(Q-1)，相当于刨去a[i]点不走。
5.在check函数里，

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110000;
int a[N];
int n,k;
bool check(int L,int Q)
{
    for(int i=1;i<=k;i++)
    {
        if(a[i]<=Q+L) //L+Q >= a[i]说明左区间+扫描区间大于等于当前a[i]，能扫到a[i],或者说a[i]扫描范围能接上L
        {
            if(a[i]<=L) //a[i]<=L 说明a[i]点在扫描的范围左边，已经过去了，  
            {
                L=a[i] + Q -1; //Q是包含a[i]这个点本身的区间长度，
                //如果a[i]在左边界左边，那a[i]的扫描范围全部用来扫描右区间，不要忘记-1：Q-1=扫描总长度-a[i]点本身
            }
            else if(a[i] > L) //a[i]在左边界的右边
            {
                L=a[i] + Q -(a[i]-L);
            }
        }
        else return false;//a[i] > Q+L说明以现在的机器人a[i]扫描范围Q都接不上左边界L
    }
    if(L<n) return false;//左边界没有扫描完整个 没考虑到为什么
    return true;
}
int main()
{
    
    cin>>n>>k;
    for(int i=1;i<=k;i++) cin>>a[i];
    int Q,L;// Q:每个机器人能扫到的区间大小。L：左边界，L左边的代表已经全部被扫过
    sort(a+1,a+1+k);
      Q=max(n/k,a[1]);
    for(Q;Q<=n;Q++)
    {
        L=0;
        //cout<<Q<<" ";
        if(check(L,Q)) break;
    }
    cout<<2*(Q-1);
}

1天内再写发现的问题
1.忘记排序
2.排序应该是k个数排序，我排了n个。
3.更加清晰了是求大于等于，故用模板一。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std; 
const int N = 1e5+10;
int n,k;
int a[N];
bool check(int x)
{
    int L = 0;
    int Q = x;
    for(int i=1;i<=k;i++)
    {
        if(L + Q < a[i]) return false;
        if(a[i] > L)
            L += Q;
        else
        {
            L=a[i] + Q -1;
        }
    }
    if(L < n) return false;
    return true;
}
int main()
{
    cin>>n>>k;  //n是总长度, k是机器人个数
    for(int i=1;i<=k;i++) scanf("%d",&a[i]);
    sort(a+1,a+1+k); //k个数，你怎么按n排序！必须先排序！
    int l=1,r=n;
    while(l<r)
    {
        int mid=(l+r)>>1;
        cout<<l<<" "<<r<<" "<<mid<<endl;
        if(check(mid)) r=mid; // a[mid] <= target 
        else l=mid+1;
        cout<<2*(l-1)<<endl;
    }
    cout<<2*(l-1);
}