现如今大数据与AI人工智能已是大行其道，大数据挖掘与分析、智能大模型的实现，它门的原理与算法可谓“甚嚣尘上”，其最为关键的高等数学部分，让我们有点不知所措。为此，将高数应用广泛的部分内容，比如：多元微积分、概率论与数理统计、线性代数，分享给大家，以共勉之。

教学目的：学习并掌握关于导数与偏导数、梯度与海森矩阵、最速下降法、随机梯度下降法等

                   原理与应用。

教学重点：梯度与海森矩阵、最速下降法

教学难点：梯度与海森矩阵、最速下降法原理与应用

教学内容：导数与偏导数、梯度与海森矩阵、最速下降法、随机梯度下降法

一、导数与偏导数

1. 导数定义

设函数 y=f(x) 在点 x0 的某个邻域内有定义，当自变量 x 在 x0 处取得增量 Δx (点 x0+Δx 仍在该邻域内)时，相应地，因变量取得增量 Δy=f(x0+Δx)−f(x0) ；如果当 Δx→0 时， Δy 与 Δx 之比的极限存在，那么称函数 y=f(x) 在点 x0 处可导，并称这个极限为函数y=f(x)在点 x0 处的导数 ，记为 f′( x0 ) ，即

也可记作

，函数 f(x) 在点x0 处可导有时也说成 f(x) 在点x0 具有导数或导数存在。

导数是描述函数的变化率的，如果 Δy 越大，而 Δx 越小，则说明函数变化很快，变化率大，即导数大。

如果极限

不存在，就说函数 y=f(x) 在点 x0 处 不可导 。

2. 导函数

函数 y=f(x) 在 开区间K内的每点处都可导 ，那么就称函数 f(x) 在开区间K内可导。

如果函数 f(x) 在开区间 (a,b) 内可导，且 f+′(a) ， f−′(b) 都存在，那么就说 f(x) 在闭区间 [a,b] 上可导。

这时，对于任一 x∈K都对应着 f(x) 的一个确定的导数值。

这样就构成了一个新的函数，这个函数叫做原来函数 y=f(x) 的导函数 ，记作 f′(x) 。

函数 f(x) 在点 x0 处的导数 f(′x0) 就是导函数 f′(x) 在点 x=x0处的函数值，即 f′(x0)=f′(x)|x=x0 。

3. 单侧导数

根据函数 f(x) 在点 x0处的导数 f′(x0) 的定义，导数

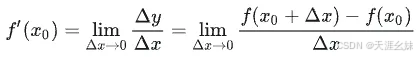
是一个极限，而 极限存在的充分必要条件是左、右极限都存在且相等 ，因此 f′(x0) 存在即 f(x) 在点 x0 处可导的充分必要条件是左、右极限

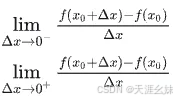
都存在且相等。

这两个极限分别称为函数 f(x) 在点 x0处的左导数和右导数（ 左右导数统称为单侧导数 ），记作 f−′(x0) 及 f+′(x0) ，即

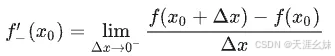
现在可以说， 一元函数f(x)在点x0处可导的充分必要条件是左导数f−′(x0)和右导数f+′(x0)都存在且相等 。

4. 函数可导性与连续性的关系

设函数 y=f(x) 在点 x 处可导，即

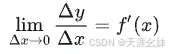
存在。由具有极限的函数与无穷小的关系知道

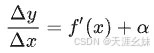
其中α为当 Δx→0 时的无穷小。上式两边同乘 Δx ，得

由此可见，当 Δx→0 时， Δy→0 ，即函数 y=f(x) 在点 x 处是连续的。

所以， 如果函数y=f(x)在点x处可导，那么函数在该点必连续。

反之一个函数在某点连续却不一定在该点可导，如y=|x| 。

5. 偏导数

以二元函数z=f(x,y) 为例，如果只有自变量 x变化，而自变量y固定( 即看做常量 )，这时二元函数z=f(x,y) 就是x的一元函数，这函数对x的导数，就称为二元函数z=f(x,y) 对于 x 的偏导数 。

定义：

设函数z=f(x,y) 在点 (x0,y0) 的某一邻域内有定义，当y固定在y0而x在x0处有增量Δx时，相应的函数有增量 f(x0+Δx,y0)−f(x0,y0)，

如果极限

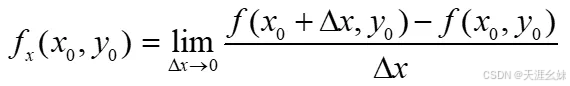
存在，那么称此极限为函数 z=f(x,y) 在点 (x0,y0) 处对 x 的偏导数，记作 fx(x0,y0) 。

类似地，有函数z=f(x,y)在点(x0,y0)处对y的偏导数，可以定义为

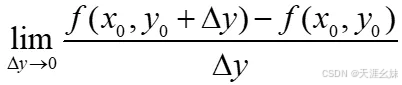
记作为fy(x0,y0) 。

如果函数z=f(x,y) 在区域D内每一点(x,y)处对x的偏导数都存在，那么这个偏导数就是x,y的函数，它就称为函数z=f(x,y)对自变量x的偏导函数，记作 fx(x,y) 。

类似地，可以定义函数z=f(x,y)对自变量y的偏导函数，记作 fy(x,y) 。

由偏导函数的概念可知，f(x,y)在点 (x0,y0) 处对x的偏导数fx′(x0,y0) ，显然就是偏导函数fx(x,y) 在点 (x0,y0) 处的函数值； fy(x0,y0) 就是偏导函数 fy(x,y) 在点 (x0,y0) 处的函数值。

6. 偏导数的几何意义

设曲面的方程为 z=f(x,y0) ，M0(x0,y0,f(x0,y0)) 为曲面 z=f(x,y) 上的一点，过 点M0 作平面 y=y0 ，截此曲面得一曲线，其方程为：

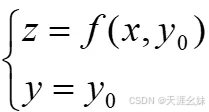
则偏导数 fx(x0,y0) 表示上述曲线在点M0处的切线 M0Ty对x轴正向的斜率，如图

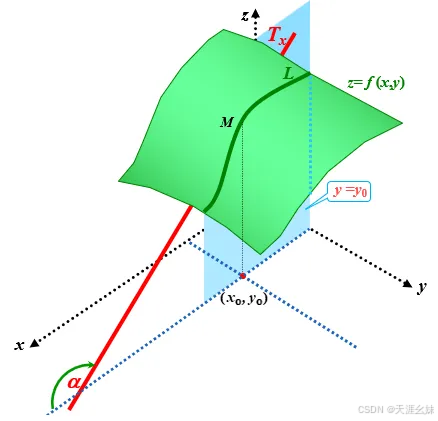
同理，偏导数 fy(x0,y0) 的几何意义是曲面被平面 x=x0所截得的曲线在点 M0 处的切线 M0Ty 对y轴的正向斜率，如图

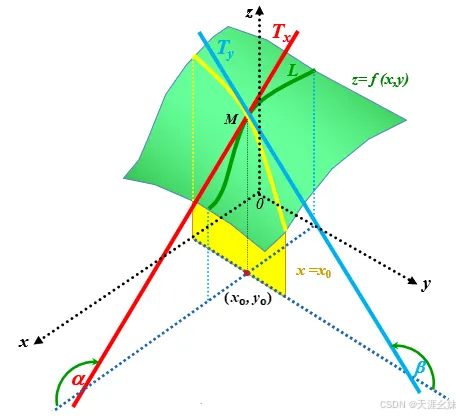
7. 多元函数的可导性与连续性

已知如果一元函数在某点具有导数，那么它在该点必定连续。但对于多元函数来说，即使各偏导数在某点都存在，也不能保证函数在该点是连续 。

这是因为各偏导数的存在只能保证点P沿着平行于坐标轴的方向趋于 P0 时，函数值 f(P) 趋于 f( P0 ) ，但不能保证点P按任何方向趋于P0时，函数值f(P)都趋于 f( P0 ) 。

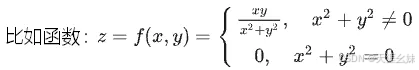
此时fx(0,0) 和 fy(0,0) 都为0，但在 (0,0) 点不连续。

二、梯度与海森矩阵

根据偏导数的定义，当对某个变量求偏导数时，函数中的所有其他变量要被当作常数。即把函数当作只含该变量的一元函数，然后根据一元函数的求导法则进行求导即可。这样二元函数的偏导数定义可以推广到三元函数和多元函数，它们的偏导数求解都是类似的。

定义2.1

记n元实函数f:Rn->R,x∈Rn为f(x)，其中x=(x1,x2,...,xn)是n维自变量，如果f(x)在每一分量xi(i=1,2,...n)一阶可导，即偏导数

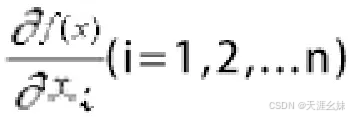
都存在，则称f(x)在点x处一阶可导，并且把偏导数组成的向∇f(x)=

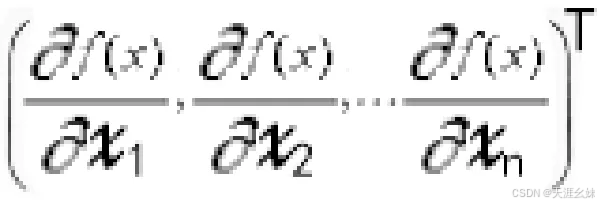
称为f(x)在点x处的一阶导数，也即梯度，常记为∇f(x)。

例2.1

已知某电阻的阻值R依赖于四个因素x1，x2，x3，x4，其函数关系为

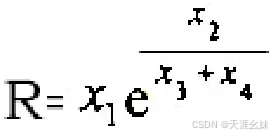
，求该函数关系的梯度。

解：分别求各个自变量的偏导数如下：

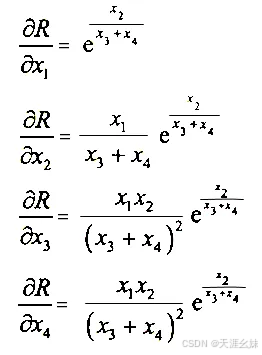
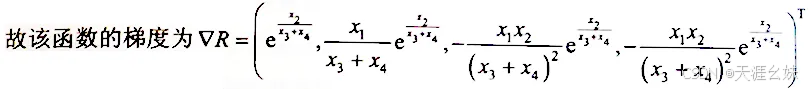
在一元涵数中， 对一阶导数再求一次导数就可以得出函数的二阶导数。和一元函数类似， 在多元函数一阶导数的基础上再求一次导数同样可以求出函数的二阶导数。

定义2.2

记n元实函数f:Rn->R,x∈Rn为f(x)，其中x=(x1,x2,...,xn)是n维自变量。如果f(x)在每一个分量xi(i=1,2,...n)二阶可导，即二阶偏导数

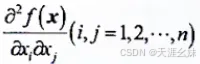
都存在，则称f(x)在点x处二阶可导， 并且把偏导数组成的矩阵 ∇2f(x)=

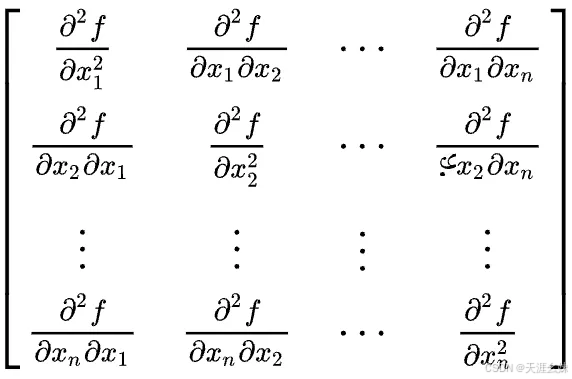
称为点f(x)在点x处的二阶导数，也称海森矩阵(Hesse)，常记作 ∇2f(x)。

例2.2

设A∈R nxn是对称矩阵，B∈R n是向量，C ∈R是常数，则二次型可以表示成函数

求该二次函数的梯度和海森矩阵。

解：

函数f(x)的梯度∇f(x)=Ax+B

函数f(x)的海森矩阵∇2f(x)=A

三、最速下降法

1、定义与作用

最速下降一般是指梯度下降，而梯度下降是迭代法的一种，可以用于求解最小二乘问题（线性和非线性都可以）。

在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。

梯度下降法(gradient descent)是一个最优化算法，常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。

2、求解过程

梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

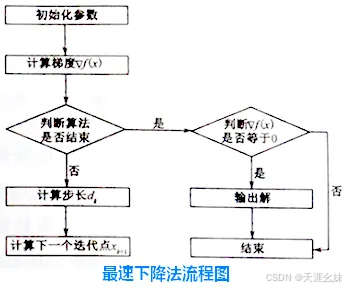
其迭代公式为：

,其中代表梯度负方向，ρk表示梯度方向上的搜索步长。

梯度方向可以通过对函数求导得到，步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标看做是ak+1的函数，然后求满足f(ak+1)的最小值的ak+1即可。

因为一般情况下，梯度向量为0说明是到了一个极值点，此时梯度的幅值也为0，而采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0即可，可以设置个非常小的常数阈值。

四、随机梯度下降法

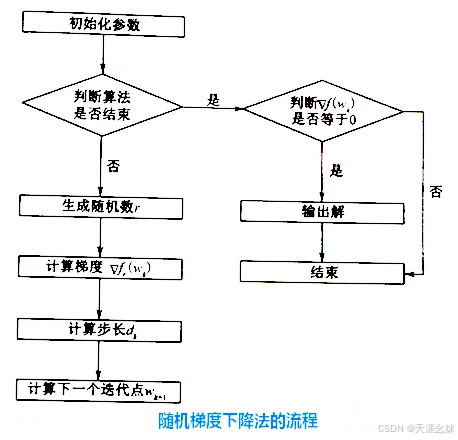
‌随机梯度下降法（Stochastic Gradient Descent，‌SGD）是一种优化算法，常用于‌机器学习和‌大数据分析中。

与传统的批量梯度下降法不同，SGD每次迭代时，不是使用整个数据集来计算梯度并更新模型参数，而是随机选择一个样本来计算梯度并进行参数更新。这种方法的主要优点是计算效率高，能够在线更新模型参数，适合处理大规模数据集。

由于每次更新可能不会按照正确的方向进行，SGD可能会导致优化波动，但这也有助于跳出局部最优解，寻找更好的解。

SGD已成功应用于支持‌向量机、‌逻辑回归等线性分类器的学习，以及‌文本分类和‌自然语言处理中的大规模和稀疏机器学习问题，因此在人工智能方面应用非常广泛。

更多精彩内容请关注本站！！！