有限元计算过程中积分点应力如何外插至节点处?【公式推导篇】
有限元计算过程中,单元积分点应力如何外推至节点?
本次分享的是:有限元计算过程中,单元积分点应力如何外推至节点?
原文链接:有限元计算过程中积分点应力如何外插至节点处?【公式推导篇】
有关积分点与节点的概念可点击跳转阅读历史推文:有限元基本概念-【节点和积分点】:
,现科普一下Q4单元、Q8单元、Q9单元的形函数和高斯积分方案。
Q4单元
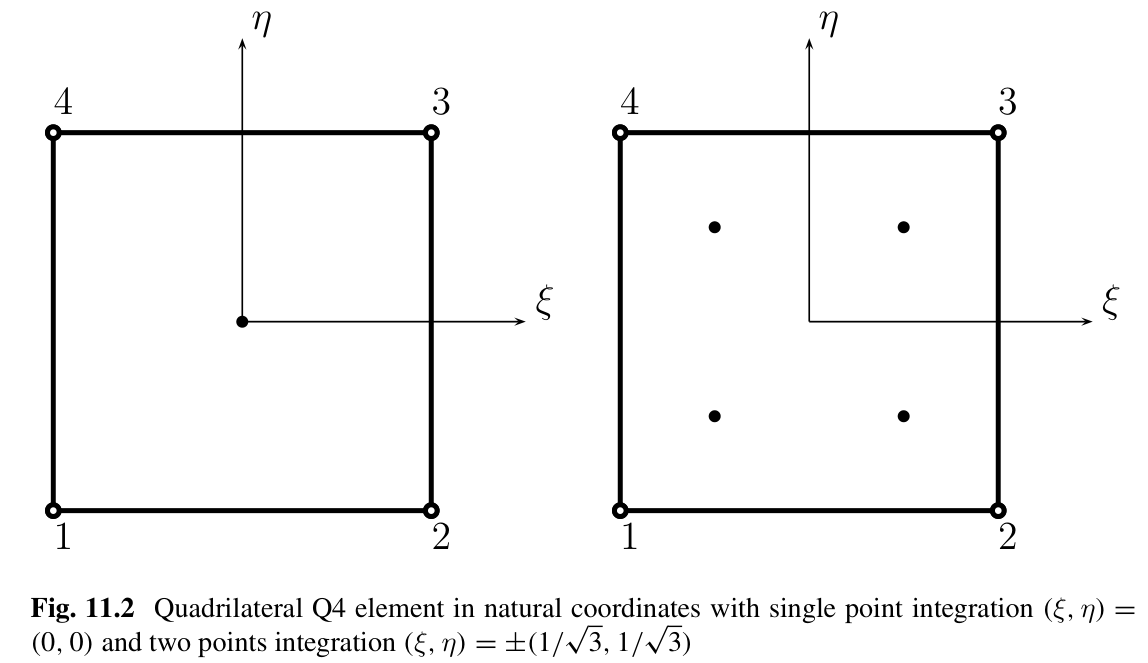
{ N 1 ( ξ , η ) = 1 4 ( 1 − ξ ) ( 1 − η ) N 2 ( ξ , η ) = 1 4 ( 1 + ξ ) ( 1 − η ) N 3 ( ξ , η ) = 1 4 ( 1 + ξ ) ( 1 + η ) N 4 ( ξ , η ) = 1 4 ( 1 − ξ ) ( 1 + η ) \begin{cases} N_1(\xi ,\eta )=\frac{1}{4}(1-\xi )(1-\eta )\\ N_2(\xi ,\eta )=\frac{1}{4}(1+\xi )(1-\eta )\\ N_3(\xi ,\eta )=\frac{1}{4}(1+\xi )(1+\eta )\\ N_4(\xi ,\eta )=\frac{1}{4}(1-\xi )(1+\eta )\\ \end{cases} ⎩ ⎨ ⎧N1(ξ,η)=41(1−ξ)(1−η)N2(ξ,η)=41(1+ξ)(1−η)N3(ξ,η)=41(1+ξ)(1+η)N4(ξ,η)=41(1−ξ)(1+η)
Q8/9单元

N 1 ( ξ , η ) = − 0.25 ( 1 − ξ ) ( 1 − η ) ( 1 + ξ + η ) N 2 ( ξ , η ) = − 0.25 ( 1 + ξ ) ( 1 − η ) ( 1 − ξ + η ) N 3 ( ξ , η ) = − 0.25 ( 1 + ξ ) ( 1 + η ) ( 1 − ξ − η ) N 4 ( ξ , η ) = − 0.25 ( 1 − ξ ) ( 1 + η ) ( 1 + ξ − η ) N 5 ( ξ , η ) = 0.5 ( 1 − ξ 2 ) ( 1 − η ) N 6 ( ξ , η ) = 0.5 ( 1 + ξ ) ( 1 − η 2 ) N 7 ( ξ , η ) = 0.5 ( 1 − ξ 2 ) ( 1 + η ) N 8 ( ξ , η ) = 0.5 ( 1 − ξ ) ( 1 − η 2 ) \begin{aligned} &N_{1}(\xi,\eta) =-0.25(1-\xi)(1-\eta)(1+\xi+\eta) \\ &N_{2}(\xi,\eta) =-0.25(1+\xi)(1-\eta)(1-\xi+\eta) \\ &N_{3}(\xi,\eta) =-0.25(1+\xi)(1+\eta)(1-\xi-\eta) \\ &N_{4}(\xi,\eta) =-0.25(1-\xi)(1+\eta)(1+\xi-\eta) \\ &N_{5}(\xi,\eta) =0.5(1-\xi^2)(1-\eta) \\ &N_{6}(\xi,\eta) =0.5(1+\xi)(1-\eta^2) \\ &N_{7}(\xi,\eta) =0.5(1-\xi^2)(1+\eta) \\ &N_{8}(\xi,\eta) =0.5(1-\xi)(1-\eta^2) \end{aligned} N1(ξ,η)=−0.25(1−ξ)(1−η)(1+ξ+η)N2(ξ,η)=−0.25(1+ξ)(1−η)(1−ξ+η)N3(ξ,η)=−0.25(1+ξ)(1+η)(1−ξ−η)N4(ξ,η)=−0.25(1−ξ)(1+η)(1+ξ−η)N5(ξ,η)=0.5(1−ξ2)(1−η)N6(ξ,η)=0.5(1+ξ)(1−η2)N7(ξ,η)=0.5(1−ξ2)(1+η)N8(ξ,η)=0.5(1−ξ)(1−η2)
N 1 ( ξ , η ) = − 0.25 ξ η ( ξ − 1 ) ( η − 1 ) N 2 ( ξ , η ) = − 0.25 ξ η ( ξ + 1 ) ( η − 1 ) N 3 ( ξ , η ) = − 0.25 ξ η ( ξ + 1 ) ( η + 1 ) N 4 ( ξ , η ) = − 0.25 ξ η ( ξ − 1 ) ( η + 1 ) N 5 ( ξ , η ) = 0.5 η ( 1 − ξ 2 ) ( η − 1 ) N 6 ( ξ , η ) = 0.5 ξ ( ξ + 1 ) ( 1 − η 2 ) N 7 ( ξ , η ) = 0.5 η ( 1 − ξ 2 ) ( η + 1 ) N 8 ( ξ , η ) = 0.5 ξ ( ξ − 1 ) ( 1 − η 2 ) N 9 ( ξ , η ) = ( 1 − ξ 2 ) ( 1 − η 2 ) \begin{aligned}&N_1(\xi,\eta)=-0.25\xi\eta(\xi-1)(\eta-1)\\&N_2(\xi,\eta)=-0.25\xi\eta(\xi+1)(\eta-1)\\&N_3(\xi,\eta)=-0.25\xi\eta(\xi+1)(\eta+1)\\&N_4(\xi,\eta)=-0.25\xi\eta(\xi-1)(\eta+1)\\&N_5(\xi,\eta)=0.5\eta(1-\xi^2)(\eta-1)\\&N_6(\xi,\eta)=0.5\xi(\xi+1)(1-\eta^2)\\&N_7(\xi,\eta)=0.5\eta(1-\xi^2)(\eta+1)\\&N_8(\xi,\eta)=0.5\xi(\xi-1)(1-\eta^2)\\&N_9(\xi,\eta)=(1-\xi^2)(1-\eta^2)\end{aligned} N1(ξ,η)=−0.25ξη(ξ−1)(η−1)N2(ξ,η)=−0.25ξη(ξ+1)(η−1)N3(ξ,η)=−0.25ξη(ξ+1)(η+1)N4(ξ,η)=−0.25ξη(ξ−1)(η+1)N5(ξ,η)=0.5η(1−ξ2)(η−1)N6(ξ,η)=0.5ξ(ξ+1)(1−η2)N7(ξ,η)=0.5η(1−ξ2)(η+1)N8(ξ,η)=0.5ξ(ξ−1)(1−η2)N9(ξ,η)=(1−ξ2)(1−η2)
应力外插
核心理念:坐标系的转换。
假设 ( ξ , η ) \left( \xi ,\eta \right) (ξ,η)是母单元的自然坐标系, ( ξ ^ , η ^ ) \left( \hat{\xi},\hat{\eta} \right) (ξ^,η^)是由高斯积分点控制的坐标系(术语可能不专业),假设高斯积分方案为 2 × 2 2 \times2 2×2。坐标系转换关系:
( ξ , η ) = ( ξ ^ , η ^ ) / 3 o r ( ξ ^ , η ^ ) = ( ξ , η ) 3 (\xi,\eta)=(\hat{\xi},\hat{\eta})/\sqrt{3}\quad\mathrm{or}\quad(\hat{\xi},\hat{\eta})=(\xi,\eta)\sqrt{3} (ξ,η)=(ξ^,η^)/3or(ξ^,η^)=(ξ,η)3
单元内任一点的应力 σ P \sigma _P σP,由4个高斯积分点应力 σ G i \sigma _{Gi} σGi进行插值时,可表示为
σ P = ∑ i = 1 4 N i σ G i = [ N 1 ( ξ ^ , η ^ ) N 2 ( ξ ^ , η ^ ) N 3 ( ξ ^ , η ^ ) N 4 ( ξ ^ , η ^ ) ] [ σ G 1 σ G 2 σ G 3 σ G 4 ] \sigma_{P}=\sum_{i=1}^{4}N_{i}\sigma_{Gi}=\begin{bmatrix}N_{1}(\hat{\xi},\hat{\eta})N_{2}(\hat{\xi},\hat{\eta})N_{3}(\hat{\xi},\hat{\eta})N_{4}(\hat{\xi},\hat{\eta})\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix} σP=i=1∑4NiσGi=[N1(ξ^,η^)N2(ξ^,η^)N3(ξ^,η^)N4(ξ^,η^)] σG1σG2σG3σG4
其中, N ( ξ ^ , η ^ ) N(\hat{\xi},\hat{\eta}) N(ξ^,η^)是基于高斯积分点的形函数,第一个积分点的坐标在母单元坐标系下为(-1,-1),根据上述的坐标系转换的方式,在高斯积分点的坐标系下,第一个单元节点在高斯积分点坐标系下坐标为 ( − 3 , − 3 ) \left( -\sqrt{3},-\sqrt{3} \right) (−3,−3) ,将此坐标值代入第一个形函数,得 1 + 3 2 1+\frac{\sqrt{3}}{2} 1+23,相同的道理,可推导至四个节点在4个形函数下的 4 × 4 4 \times 4 4×4外插矩阵:
[ σ 1 σ 2 σ 3 σ 4 ] = [ 1 + 0.5 3 − 0.5 1 − 0.5 3 − 0.5 − 0.5 1 + 0.5 3 − 0.5 1 − 0.5 3 1 − 0.5 3 − 0.5 1 + 0.5 3 − 0.5 − 0.5 1 − 0.5 3 − 0.5 1 + 0.5 3 ] [ σ G 1 σ G 2 σ G 3 σ G 4 ] \begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\end{bmatrix}=\begin{bmatrix}1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}&-0.5\\-0.5&1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}\\1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}&-0.5\\-0.5&1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix} σ1σ2σ3σ4 = 1+0.53−0.51−0.53−0.5−0.51+0.53−0.51−0.531−0.53−0.51+0.53−0.5−0.51−0.53−0.51+0.53 σG1σG2σG3σG4
对于Q8、Q9单元,依然可采用 2 × 2 2 \times 2 2×2高斯积分方案(减缩积分)。
相应形函数外插矩阵:
[ σ 1 σ 2 σ 3 σ 4 σ 5 σ 6 σ 7 σ 8 ] = [ 1 + 0.5 3 − 0.5 1 − 0.5 3 − 0.5 − 0.5 1 + 0.5 3 − 0.5 1 − 0.5 3 1 − 0.5 3 − 0.5 1 + 0.5 3 − 0.5 − 0.5 1 − 0.5 3 − 0.5 1 + 0.5 3 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 ] [ σ G 1 σ G 2 σ G 3 σ G 4 ] \begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\\\sigma_5\\\sigma_6\\\sigma_7\\\sigma_8\end{bmatrix}=\begin{bmatrix}1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}&-0.5\\-0.5&1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}\\1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}&-0.5\\-0.5&1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}\\(1+\sqrt{3})/4&(1+\sqrt{3})/4&(1-\sqrt{3})/4&(1-\sqrt{3})/4\\(1-\sqrt{3})/4&(1+\sqrt{3})/4&(1+\sqrt{3})/4&(1-\sqrt{3})/4\\(1-\sqrt{3})/4&(1-\sqrt{3})/4&(1+\sqrt{3})/4&(1+\sqrt{3})/4\\(1+\sqrt{3})/4&(1-\sqrt{3})/4&(1-\sqrt{3})/4&(1+\sqrt{3})/4\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix} σ1σ2σ3σ4σ5σ6σ7σ8 = 1+0.53−0.51−0.53−0.5(1+3)/4(1−3)/4(1−3)/4(1+3)/4−0.51+0.53−0.51−0.53(1+3)/4(1+3)/4(1−3)/4(1−3)/41−0.53−0.51+0.53−0.5(1−3)/4(1+3)/4(1+3)/4(1−3)/4−0.51−0.53−0.51+0.53(1−3)/4(1−3)/4(1+3)/4(1+3)/4 σG1σG2σG3σG4
[ σ 1 σ 2 σ 3 σ 4 σ 5 σ 6 σ 7 σ 8 σ 9 ] = [ 1 + 0.5 3 − 0.5 1 − 0.5 3 − 0.5 − 0.5 1 + 0.5 3 − 0.5 1 − 0.5 3 1 − 0.5 3 − 0.5 1 + 0.5 3 − 0.5 − 0.5 1 − 0.5 3 − 0.5 1 + 0.5 3 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 + 3 ) / 4 ( 1 − 3 ) / 4 ( 1 − 3 ) / 4 ( 1 + 3 ) / 4 0.25 0.25 0.25 0.25 ] [ σ G 1 σ G 2 σ G 3 σ G 4 ] \begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\\\sigma_5\\\sigma_6\\\sigma_7\\\sigma_8\\\sigma_9\end{bmatrix}=\begin{bmatrix}1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}&-0.5\\-0.5&1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}\\1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}&-0.5\\-0.5&1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}\\(1+\sqrt{3})/4&(1+\sqrt{3})/4&(1-\sqrt{3})/4&(1-\sqrt{3})/4\\(1-\sqrt{3})/4&(1+\sqrt{3})/4&(1+\sqrt{3})/4&(1-\sqrt{3})/4\\(1-\sqrt{3})/4&(1-\sqrt{3})/4&(1+\sqrt{3})/4&(1+\sqrt{3})/4\\(1+\sqrt{3})/4&(1-\sqrt{3})/4&(1-\sqrt{3})/4&(1+\sqrt{3})/4\\0.25&0.25&0.25&0.25\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix} σ1σ2σ3σ4σ5σ6σ7σ8σ9 = 1+0.53−0.51−0.53−0.5(1+3)/4(1−3)/4(1−3)/4(1+3)/40.25−0.51+0.53−0.51−0.53(1+3)/4(1+3)/4(1−3)/4(1−3)/40.251−0.53−0.51+0.53−0.5(1−3)/4(1+3)/4(1+3)/4(1−3)/40.25−0.51−0.53−0.51+0.53(1−3)/4(1−3)/4(1+3)/4(1+3)/40.25 σG1σG2σG3σG4
公式推导
为了便于公式的推导,可借助Mathematica符号计算软件,编写如下代码:
(*应用2*2高斯积分方案*)
(*定义形函数(Q4)*)
l1[\[Xi]_] := (1 - \[Xi])/2
l2[\[Xi]_] := (1 + \[Xi])/2
N1[\[Xi]_, \[Eta]_] := l1[\[Xi]]*l1[\[Eta]]
N2[\[Xi]_, \[Eta]_] := l2[\[Xi]]*l1[\[Eta]]
N3[\[Xi]_, \[Eta]_] := l2[\[Xi]]*l2[\[Eta]]
N4[\[Xi]_, \[Eta]_] := l1[\[Xi]]*l2[\[Eta]]
(*将单元坐标系转换至高斯积分点坐标系*)
nodeQ4 = Sqrt[3] {{-1, -1}, {1, -1}, {1, 1}, {-1, 1}};
nodeQ8 = Sqrt[3] {
{-1, -1}, {1, -1}, {1, 1}, {-1, 1},(*corner nodes*)
{0, -1}, {1, 0}, {0, 1}, {-1, 0} (*mid-
side nodes*)
};
nodeQ9 = Sqrt[3] {
{-1, -1}, {1, -1}, {1, 1}, {-1, 1},(*corner nodes*)
{0, -1}, {1, 0}, {0, 1}, {-1, 0},(*mid-side nodes*)
{0, 0} (*center node*)
};
(*计算高斯积分点参考坐标系下的形函数外插矩阵*)
extrapolationMatrix =
Table[{N1[\[Xi], \[Eta]], N2[\[Xi], \[Eta]], N3[\[Xi], \[Eta]],
N4[\[Xi], \[Eta]]} /. {\[Xi] -> p[[1]], \[Eta] -> p[[2]]}, {p,
nodeQ4}] // Expand;
(*矩阵形式展现*)
MatrixForm[extrapolationMatrix]
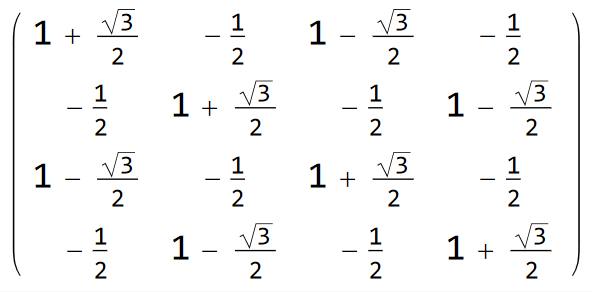
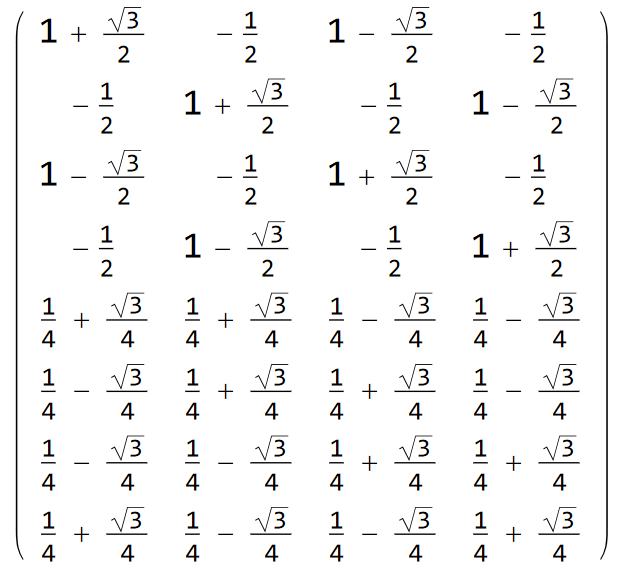

以上是有关应力外插的理论知识,如何将之添加到我们的有限元代码中,我会在后续的推文中一步一步数值实现,感谢你的阅读!

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)