机器人动力学仿真求力矩,附matlab代码
机器人动力学仿真求力矩,matlab代码。
·
机器人动力学仿真求力矩,matlab代码
一、理论基础
拉格朗日法和牛顿欧拉法对比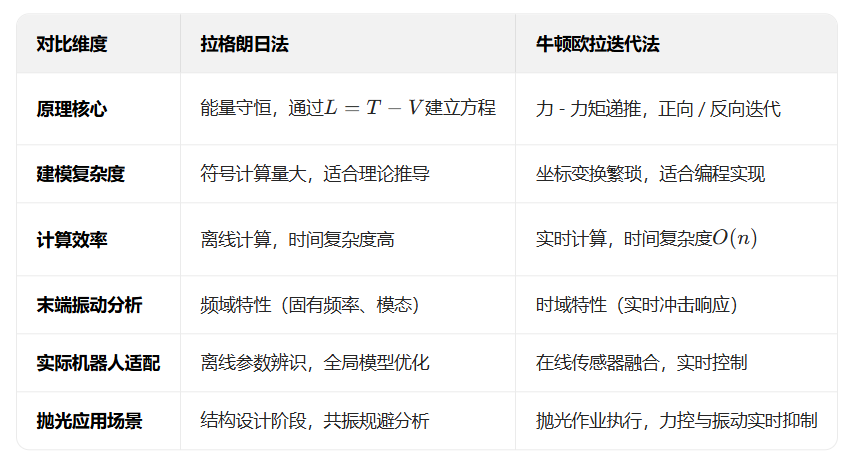
二、代码实现
这段代码实现了一个基于牛顿 - 欧拉迭代法的机器人动力学算法,用于计算机器人在给定关节状态下所需的驱动力矩。
该代码实现了牛顿 - 欧拉逆动力学算法的核心逻辑:
- 外推阶段:通过递归计算各连杆的速度和加速度,建立运动学关系。
- 内推阶段:基于运动学结果和连杆物理参数,计算为实现给定运动所需的关节力矩。
该算法适用于:
- 机器人轨迹规划中的力矩前馈控制。
- 关节电机选型(确定最大驱动力矩需求)。
- 动力学仿真(预测机器人在不同运动下的响应)。
function Torque = dynamics(angle, angular_v, angular_a)
% 质量矩阵,unit:Kg
mass = [65.0, 50.0, 20.0, 10.5, 3.5, 1.0];
% 杆件参数,unit:m
P1 = 0.43;
P2 = 0.0996;
P4 = 0.6507;
P5 = 0.0011;
P6 = 0.7002;
% 质心在杆件坐标系下的表示,unit:m
PC = [ -0.028, -0.014, -0.093;
0.281, -0.023, 0.121;
0.0, -0.049, -0.014;
0.002, 0.006, -0.254;
-0.001, -0.047, 0.005;
0.0001, 0.004, 0.130;];
% 下一个坐标系在上一个坐标系下的表示
P = [0.0, 0.0, P1;
-P2, 0.0, 0.0;
P4, 0.0, 0.0;
P5, -P6, 0.0;
0.0, 0.0, 0.0;
0.0, 0.0, 0.0;];
% 杆件在质心坐标系下的惯性张量 unit:kg*m^2
IC(:,:,1) = [1.3 0.0 0.0;
0.0 0.9 0.0;
0.0 0.0 0.8];
IC(:,:,2) = [2.9 0.0 0.0;
0.0 2.8 0.0;
0.0 0.0 0.2];
IC(:,:,3) = [0.22 0.0 0.0;
0.0 0.22 0.0;
0.0 0.0 0.17];
IC(:,:,4) = [0.32 0.0 0.0;
0.0 0.32 0.0;
0.0 0.0 0.0];
IC(:,:,5) = [0.002 0.0 0.0;
0.0 0.002 0.0;
0.0 0.0 0.002];
IC(:,:,6) = [0.002 0.0 0.0;
0.0 0.002 0.0;
0.0 0.0 0.0004];
% 获取杆件间的旋转矩阵(i+1在i下的表示)
R(:,:,1) = [cos(angle(1)), -sin(angle(1)), 0.0;
sin(angle(1)), cos(angle(1)), 0.0;
0.0, 0.0, 1.0];
R(:,:,2) = [sin(angle(2)), cos(angle(2)), 0.0;
0.0, 0.0, 1.0;
cos(angle(2)), -sin(angle(2)), 0.0];
R(:,:,3) = [cos(angle(3)), -sin(angle(3)), 0.0;
sin(angle(3)), cos(angle(3)), 0.0;
0.0, 0.0, 1.0];
R(:,:,4) = [cos(angle(4)), -sin(angle(4)), 0.0;
0.0, 0.0, -1.0;
sin(angle(4)), cos(angle(4)), 0.0];
R(:,:,5) = [cos(angle(5)), -sin(angle(5)), 0.0;
0.0, 0.0, 1.0;
-sin(angle(5)), -cos(angle(5)), 0.0];
R(:,:,6) = [cos(angle(6)), -sin(angle(6)), 0.0;
0.0, 0.0, -1.0;
sin(angle(6)), cos(angle(6)), 0.0];
% 获取杆件间的旋转逆矩阵(i在i+1下的表示)
for i1 = 1:6
inR(:,:,i1) = inv(R(:,:,i1));
end
% 迭代初始化
% 基座角速度为0
omiga_v0 = [0;0;0];
% 基座角加速度为0
omiga_a0 = [0;0;0];
% 基座线加速度为0
acc0 = [0;0;0];
% 外推,求杆件1~6的角速度,线加速度,角加速度
for i = 1:6
if i == 1
% 求杆件1角速度
z = [0;0;angular_v(i)];
omiga_v(:,i) = ones(3,3)*omiga_v0 + z;
% 求杆件1角加速度
za = [0;0;angular_a(i)];
omiga_a(:,i) = ones(3,3)*omiga_a0 +cross(ones(3,3)*omiga_v0, z)+ za;
% 求杆件1线加速度
acc(:,i) = ones(3,3)*(cross(omiga_a0, P(i,:)') + cross(omiga_v0, cross(omiga_v0, P(i,:)')) + acc0);
else
% 求杆件2~6角速度
z = [0;0;angular_v(i)];
omiga_v(:,i) = inR(:,:,i)*omiga_v(:,i-1) + z;
% 求杆件2~6角加速度
za = [0;0;angular_a(i)];
omiga_a(:,i) = inR(:,:,i)*omiga_a(:,i-1) + cross(inR(:,:,i)*omiga_v(:,i-1), z) + za;
% 求杆件2~6线加速度
acc(:,i) = inR(:,:,i)*(cross(omiga_a(:,i-1), P(i,:)') + cross(omiga_v(:,i-1), cross(omiga_v(:,i-1), P(i,:)')) + acc(:,i-1));
end
% 求杆件1~6质心线加速度
accz(:,i) = cross(omiga_a(:,i), PC(i,:)') + cross(omiga_v(:,i), cross(omiga_v(:,i), PC(i,:)')) + acc(:,i);
% 求杆件1~6惯性力
force1(:,i) = mass(i)*accz(:,i);
% 求杆件1~6惯性力矩
torque1(:,i) = IC(:,:,i)*omiga_a(:,i) + cross(omiga_v(:,i), IC(:,:,i)*omiga_v(:,i));
end
% 末端关节受外力/力矩
force2out = [0;0;0];
torque2out = [0;0;0];
% 内推,求关节6~1的力和力矩
for i = 6:-1:1
if i == 6
% 求杆件6受到的力
force2(:,i) = ones(3,3)*force2out + force1(:,i);
% 求杆件6受到的力矩
torque2(:,i) = torque1(:,i) + ones(3,3)*torque2out + cross(PC(i,:)', force1(:,i)) + cross(zeros(3,1), ones(3,3)*force2out);
else
% 求杆件5~1受到的力
force2(:,i) = R(:,:,i+1)*force2(:,i+1) + force1(:,i);
% 求杆件5~1受到的力矩
torque2(:,i) = torque1(:,i) + R(:,:,i+1)*torque2(:,i+1) + cross(PC(i,:)', force1(:,i)) + cross(P(i+1,:)', R(:,:,i+1)*force2(:,i+1));
end
% 求关节i受力矩
Torque(i) = torque2(3,i);
end
调用该函数的指令
% 定义输入参数(关节角度、速度、加速度)
q = [pi/4, pi/6, -pi/3, pi/8, -pi/4, pi/6]; % 关节角度(弧度)
qd = [0.1, 0.2, -0.1, 0.3, -0.2, 0.1]; % 关节速度(rad/s)
qdd = [0.05, 0.1, -0.05, 0.15, -0.1, 0.05]; % 关节加速度(rad/s²)
% 计算关节力矩
Torque = dynamics(q, qd, qdd);
% 输出结果
disp('各关节所需驱动力矩:');
disp(Torque);直接运行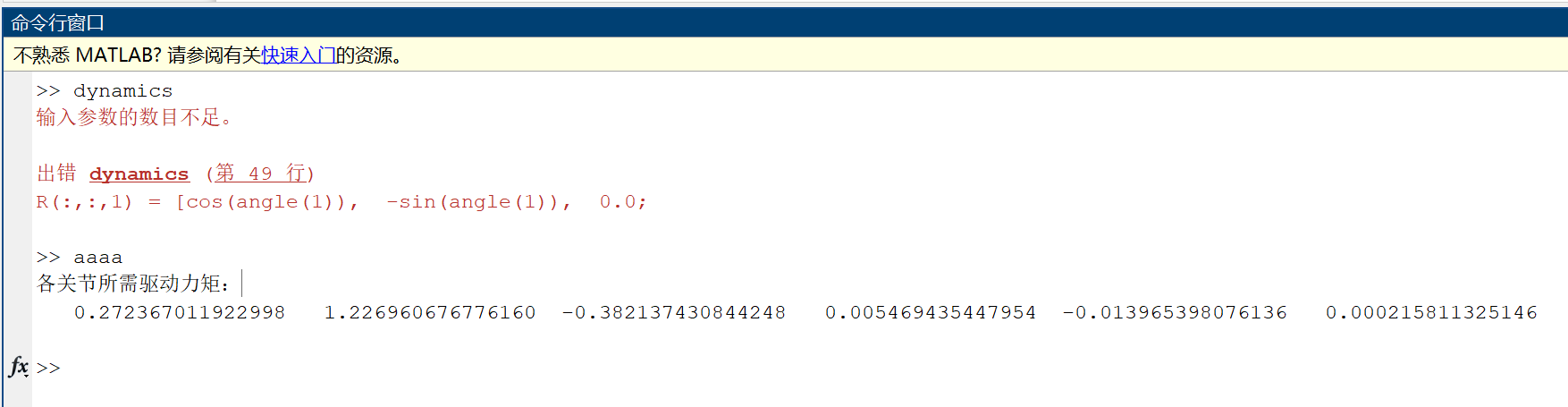

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)