使用蒙特卡罗方法计算圆周率
这个东西网上已经有很多相关的内容了, 我只是对这个过程感兴趣, 所以自己来做了一个. 网上, 大多数纯粹计算的, 对于我这种视觉型的人来说, 还是要看一下比较好. 这里我加入了 matplotlib 绘制散点图 (临时学的简单用法), 把这个过程用图片表示出来. 虽然已经理解了它计算的原理, 但是真的看到自己画出来的图示, 还是感觉满有意思的. 果然一图胜千言, 哈哈.
介绍
这个东西网上已经有很多相关的内容了, 我只是对这个过程感兴趣, 所以自己来做了一个. 网上, 大多数纯粹计算的, 对于我这种视觉型的人来说, 还是要看一下比较好. 这里我加入了 matplotlib 绘制散点图 (临时学的简单用法), 把这个过程用图片表示出来. 虽然已经理解了它计算的原理, 但是真的看到自己画出来的图示, 还是感觉满有意思的. 果然一图胜千言, 哈哈.
代码
# 使用蒙特卡洛算法计算圆周率
import random
from typing import Tuple
import matplotlib.pyplot as plt
def generateCoords() -> Tuple[float, float]:
"""随机生成范围内的坐标"""
return random.uniform(-1.0, 1.0), \
random.uniform(-1.0, 1.0)
def is_in_round(x: float, y: float):
"""判断给定坐标是否在圆内"""
return (x**2 + y**2) <= 1.0
if __name__ == "__main__":
sum = 7 # 试验总次数
total = 1 # 一次试验总次数x
hint = 0 # 命中次数
hint_x_coords = [] # 命中坐标 x
hint_y_coords = [] # 命中坐标 y
no_hint_x_coords = [] # 未命中坐标 x
no_hint_y_coords = [] # 未命中坐标 y
# 单位圆半径 1, 正方形边长为 2
for s in range(1, sum+1):
total = 10*total
hint = 0
for i in range(0, total):
x, y = generateCoords()
if is_in_round(x, y):
hint += 1
hint_x_coords.append(x)
hint_y_coords.append(y)
else:
no_hint_x_coords.append(x)
no_hint_y_coords.append(y)
# 计算圆周率
PI = 4.0*hint/total
# 绘制散点图, 首先要清空图片
plt.clf()
# 设置 x y 等长, 不然最终结果像是椭圆了
plt.axis("equal")
# 绘制命中的点
plt.scatter(hint_x_coords, hint_y_coords)
# 绘制未命中的点
plt.scatter(no_hint_x_coords, no_hint_y_coords)
# 保存图片
plt.savefig(f"{s}_{hint}_{total}.png")
print(f"{s}th Total: {total}, hint times: {hint}, PI = {PI}")
效果
7 次试验结果: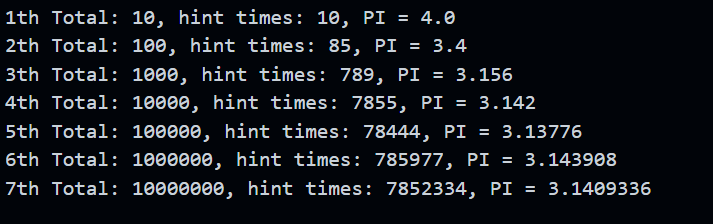
注: 推荐只做 7 次, 因为第 8 次已经耗费了将近 20 分钟了, 7 次的话, 一分钟之内结果就全部出来了.
这里可以看出来, 计算的结果是在逐渐逼近圆周率的, 但是感觉继续提高试验次数, 对于精度的提升并不是很明显. 不知道是代码是问题, 还是这个方法的问题. 而且, 我也不能一直提高精度, 毕竟在计算的时间上是不可接受的.
试验次数: 10, 命中: 10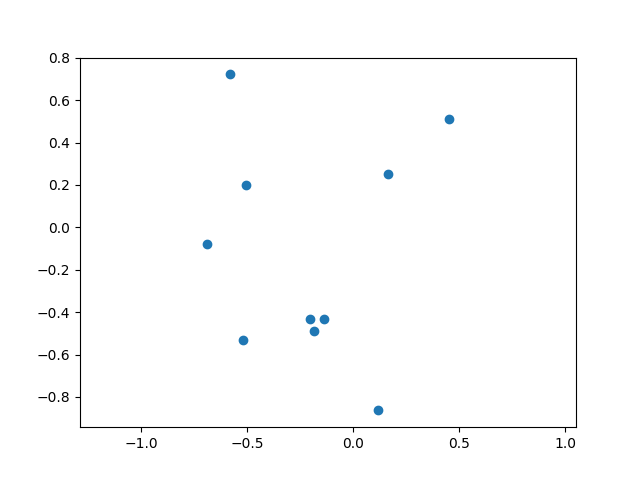
试验次数: 100, 命中: 85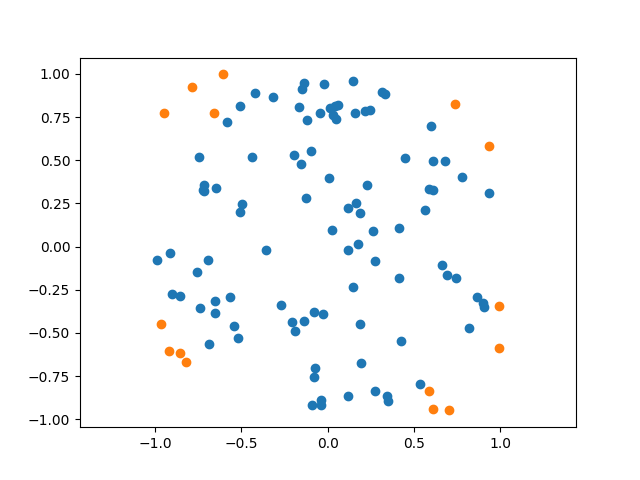
试验次数: 1000, 命中: 789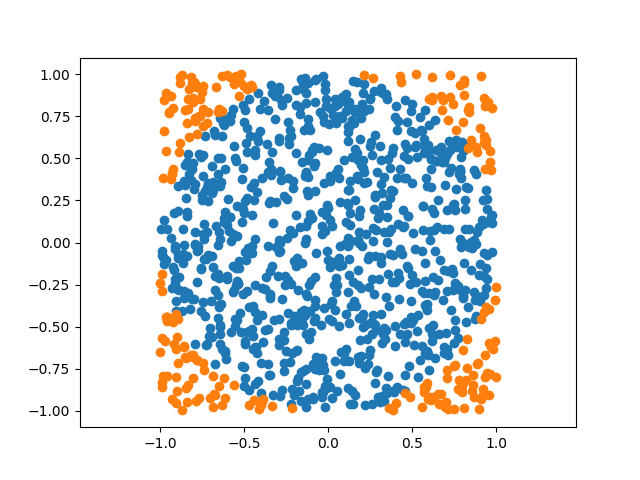
试验次数: 10000, 命中: 7855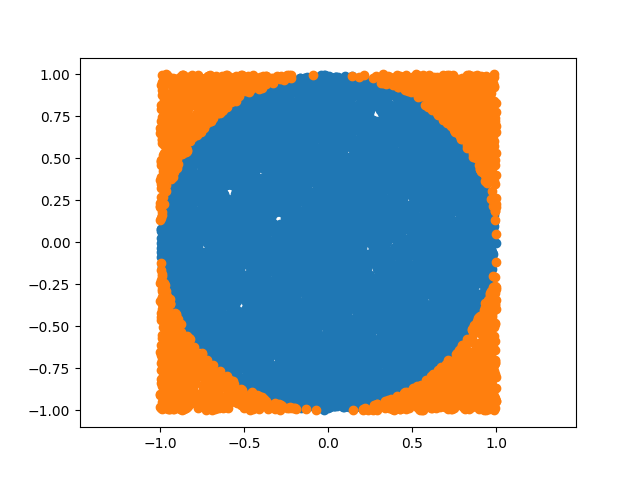
试验次数: 100000, 命中: 78444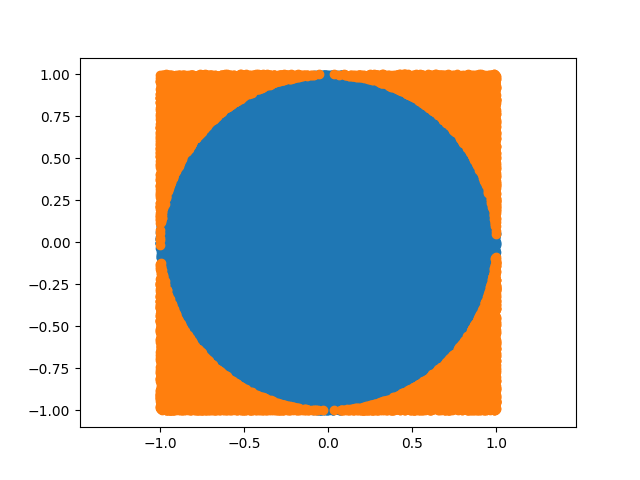
试验次数: 1000000, 命中: 785977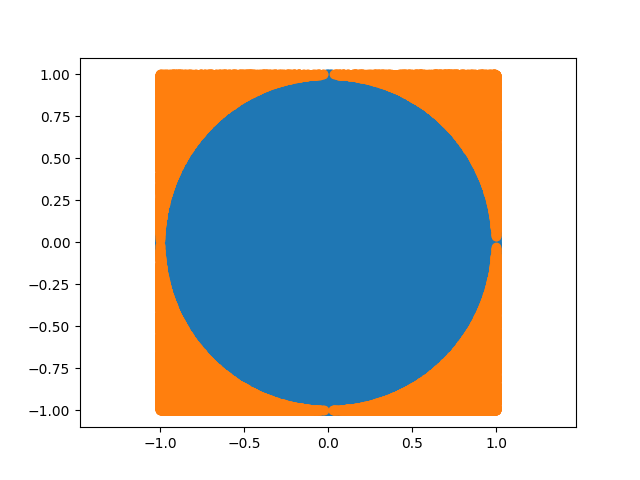
试验次数: 10000000, 命中: 7852334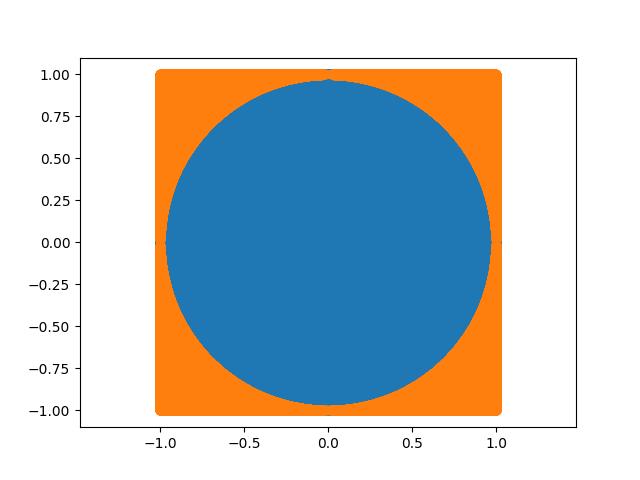

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)