1. 概述

逆波兰表达式（Reverse Polish Notation, RPN）是波兰逻辑学家J·Lukasiewicz于1929男首先提出的一种表达式的表示方法，也叫做后缀表达式。

一般的表达式又称中缀表达式，这种表达式的二元运算法放在两个操作数中间，而逆波兰表达式把运算符放在两个操作数的后面。例如 a + b 的逆波兰表达式为 ab+ 。

它的优势在于只用两种简单的操作：入栈和出战就可以搞定任何普通表达式的运算。


2. 中缀表达式转换为逆波兰表达式

将中缀表达式转换为逆波兰表达式，步骤如下：

  • 从左到右扫描算术表达式；
  • 如果遇到的是操作数，则提取出操作数，将其直接放入逆波兰表达式中；
  • 如果遇到的是操作符，则需要将栈中优先级比当前操作符优先级高的操作依次弹出并加入到逆波兰表达式中；
  • 其他字符直接跳过；

JAVA

/**
 * 拆分中缀表达式，即将整数和运算符都提取出来，去掉空格等
 *
 * @param expression 原始表达式
 * @return 拆分后的中缀表达式
 */
private List<String> splitInfixExpression(String expression) {
    List<String> res = new ArrayList<>();
    for (int i = 0; i < expression.length(); i++) {
        char c = expression.charAt(i);
        if (c == ' ') {
            continue;
        } else if (c == '+' || c == '-' || c == '*' || c == '\\' || c == '(' || c == ')') {
            res.add(String.valueOf(c));
        } else {
            int j = i + 1;
            while (j < expression.length() && Character.isDigit(expression.charAt(j))) j++;
            res.add(expression.substring(i, j));
            i = j - 1;
        }
    }
    return res;
}

/**
 * 将传入的中缀表达式转换为逆波兰表达式
 * 通常的普通表达式只有 +、-、*、/ 和 () 运算
 *
 * @param expression 中缀表达式
 * @return 你波兰表达式
 */
public List<String> toReversePolishNotation(String expression) {
    // 拆分后的中缀表达式
    List<String> infixExpression = splitInfixExpression(expression);
    // 逆波兰表达式
    List<String> res = new ArrayList<>();
    // 操作符栈
    Stack<String> stack = new Stack<>();
    for (String element: infixExpression) {
        if (isOperator(element)) {
            // 将栈中优先级比当前运算符优先级低的运算符加入逆波兰表达式中
            while (!stack.isEmpty() && getPriority(stack.peek()) > getPriority(element)) {
                res.add(stack.pop());
            }
            stack.push(element);
        } else if ("(".equals(element)) {
            // '('直接压入栈中
            stack.push(element);
        } else if (")".equals(element)) {
            // ')'，则弹出栈中元素加入到逆波兰表达式中，直到'('
            while (!"(".equals(stack.peek())) {
                res.add(stack.pop());
            }
            stack.pop(); // 去掉'('
        } else {
            // 其他情况，即为操作数的情况，则将操作数直接压入栈中
            res.add(element);
        }
    }
    while (!stack.isEmpty()) {
        if (!"(".equals(stack.peek())) {
            res.add(stack.pop());
        }
    }
    return res;
}

/**
 * 获取运算符的优先级
 */
private int getPriority(String element) {
    // '('表示括号运算开始，优先级是最低的，直接将其压入栈中
    if ("(".equals(element)) return 0;
    // '+'、'-' 运算的优先级次之
    if ("+".equals(element) || "-".equals(element)) return 1;
    // '*'、'\' 运算的优先级最高
    if ("*".equals(element) || "/".equals(element)) return 2;

    return -1;
}

private boolean isOperator(String element) {
    return "+".equals(element) || "-".equals(element) || "*".equals(element) || "/".equals(element);
}

C++

**C++**
```cpp
vector<string> splitInfixExpression(string& expression) {
    vector<string> res;
    for (int i = 0; i < expression.size(); i++) {
        char c = expression[i];
        if (c == ' ') {
            continue;
        } else if (c == '+' || c == '-' || c == '*' || c == '/' || c == '(' || c == ')') {
            res.push_back({c});
        } else {
            int j = i + 1;
            while (j < expression.size() && isdigit(expression[j])) j++;
            res.push_back(expression.substr(i, j - i));
            i = j - 1;
        }
    }
    return res;
}

vector<string> toReversePolishNotation(string& expression) {
    vector<string> res;
    stack<string> ops;
    vector<string> infixExpression = splitInfixExpression(expression);
    for (string& element: infixExpression) {
        if (isOperator(element)) {
            while (!ops.empty() && getPriority(ops.top()) > getPriority(element)) {
                auto& op = ops.top(); ops.pop();
                res.push_back(op);
            }
            ops.push(element);
        } else if (element == "(") {
            ops.push(element);
        } else if (element == ")") {
            while (ops.top() != "(") {
                auto& op = ops.top(); ops.pop();
                res.push_back(op);
            }
            ops.pop();
        } else {
            res.push_back(element);
        }
    }
    while (!ops.empty()) {
        if (ops.top() != "(") {
            res.push_back(ops.top());
            ops.pop();
        }
    }
    return res;
}

bool isOperator(string element) {
    return "+" == element || "-" == element || "*" == element || "/" == element;
}

int getPriority(string element) {
    if (element == "(") return 0;
    if (element == "+" || element == "-") return 1;
    if (element == "*" || element == "/") return 2;

    return -1;
}

3. 由逆波兰表达式计算得到结果

计算逆波兰表达式只需要一个栈就可以了，步骤如下：

  • 从左到右依次扫描逆波兰表达式；
  • 当遇到操作数时，直接将其压入栈中；
  • 当遇到操作符时，则从栈中弹出两个数作为操作数，并根据当前的运算符计算结果并压入栈中，要注意弹出的两个数，第一次弹出的操作数是运算符右边的操作数，第二次弹出的操作数是运算符左边的操作数。

JAVA

public int calculateReversePolishNotation(List<String> reversePolishNotation) {
    Stack<Integer> stack = new Stack<>();
    for (String element: reversePolishNotation) {
        if (isOperator(element)) {
            int op2 = stack.pop(), op1 = stack.pop();
            if ("+".equals(element)) stack.push(op1 + op2);
            if ("-".equals(element)) stack.push(op1 - op2);
            if ("*".equals(element)) stack.push(op1 * op2);
            if ("/".equals(element)) stack.push(op1 / op2);
        } else {
            stack.push(Integer.parseInt(element));
        }
    }
    return stack.peek();
}

C++

int calculateReversePolishNotation(vector<string>& reversePolishExpression) {
    stack<int> st;
    for (string& element: reversePolishExpression) {
        if (isOperator(element)) {
            int num2 = st.top(); st.pop();
            int num1 = st.top(); st.pop();
            if (element == "+") st.push(num1 + num2);
            if (element == "-") st.push(num1 - num2);
            if (element == "*") st.push(num1 * num2);
            if (element == "/") st.push(num1 / num2);
        } else {
            st.push(stoi(element));
        }
    }
    return st.top();
}

4. 测试

JAVA

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

/**
 * @author yumu
 * @date 2022/8/16
 */
public class ReversePolishNotation {

    /**
     * 拆分中缀表达式，即将整数和运算符都提取出来，去掉空格等
     *
     * @param expression 原始表达式
     * @return 拆分后的中缀表达式
     */
    private List<String> splitInfixExpression(String expression) {
        List<String> res = new ArrayList<>();
        for (int i = 0; i < expression.length(); i++) {
            char c = expression.charAt(i);
            if (c == ' ') {
                continue;
            } else if (c == '+' || c == '-' || c == '*' || c == '\\' || c == '(' || c == ')') {
                res.add(String.valueOf(c));
            } else {
                int j = i + 1;
                while (j < expression.length() && Character.isDigit(expression.charAt(j))) j++;
                res.add(expression.substring(i, j));
                i = j - 1;
            }
        }
        return res;
    }

    /**
     * 将传入的中缀表达式转换为逆波兰表达式
     * 通常的普通表达式只有 +、-、*、/ 和 () 运算
     *
     * @param expression 中缀表达式
     * @return 你波兰表达式
     */
    public List<String> toReversePolishNotation(String expression) {
        // 拆分后的中缀表达式
        List<String> infixExpression = splitInfixExpression(expression);
        // 逆波兰表达式
        List<String> res = new ArrayList<>();
        // 操作符栈
        Stack<String> stack = new Stack<>();
        for (String element: infixExpression) {
            if (isOperator(element)) {
                // 将栈中优先级比当前运算符优先级低的运算符加入逆波兰表达式中
                while (!stack.isEmpty() && getPriority(stack.peek()) > getPriority(element)) {
                    res.add(stack.pop());
                }
                stack.push(element);
            } else if ("(".equals(element)) {
                // '('直接压入栈中
                stack.push(element);
            } else if (")".equals(element)) {
                // ')'，则弹出栈中元素加入到逆波兰表达式中，直到'('
                while (!"(".equals(stack.peek())) {
                    res.add(stack.pop());
                }
                stack.pop(); // 去掉'('
            } else {
                // 其他情况，即为操作数的情况，则将操作数直接压入栈中
                res.add(element);
            }
        }
        while (!stack.isEmpty()) {
            if (!"(".equals(stack.peek())) {
                res.add(stack.pop());
            }
        }
        return res;
    }

    /**
     * 获取运算符的优先级
     */
    private int getPriority(String element) {
        // '('表示括号运算开始，优先级是最低的，直接将其压入栈中
        if ("(".equals(element)) return 0;
        // '+'、'-' 运算的优先级次之
        if ("+".equals(element) || "-".equals(element)) return 1;
        // '*'、'\' 运算的优先级最高
        if ("*".equals(element) || "/".equals(element)) return 2;

        return -1;
    }

    private boolean isOperator(String element) {
        return "+".equals(element) || "-".equals(element) || "*".equals(element) || "/".equals(element);
    }

    public int calculateReversePolishNotation(List<String> reversePolishNotation) {
        Stack<Integer> stack = new Stack<>();
        for (String element: reversePolishNotation) {
            if (isOperator(element)) {
                int op2 = stack.pop(), op1 = stack.pop();
                if ("+".equals(element)) stack.push(op1 + op2);
                if ("-".equals(element)) stack.push(op1 - op2);
                if ("*".equals(element)) stack.push(op1 * op2);
                if ("/".equals(element)) stack.push(op1 / op2);
            } else {
                stack.push(Integer.parseInt(element));
            }
        }
        return stack.peek();
    }

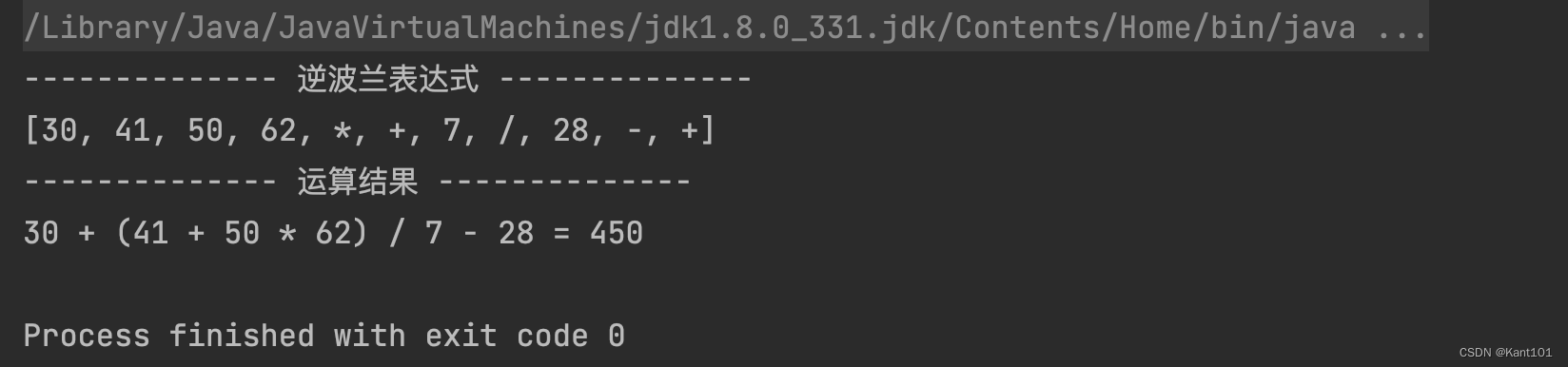
    public static void main(String[] args) {
        ReversePolishNotation reversePolishNotation = new ReversePolishNotation();
        String expression = "30 + (41 + 50 * 62) / 7 - 28";
        List<String> postFix = reversePolishNotation.toReversePolishNotation(expression);
        System.out.println("-------------- 逆波兰表达式 --------------");
        System.out.println(postFix);
        int res = reversePolishNotation.calculateReversePolishNotation(postFix);
        System.out.println("-------------- 运算结果 --------------");
        System.out.println(expression + " = " + res);
    }
}

C++

#include <iostream>
#include <vector>
#include <string>
#include <stack>

using namespace std;

class ReversePolishNotation {
public:
    vector<string> splitInfixExpression(string& expression) {
        vector<string> res;
        for (int i = 0; i < expression.size(); i++) {
            char c = expression[i];
            if (c == ' ') {
                continue;
            } else if (c == '+' || c == '-' || c == '*' || c == '/' || c == '(' || c == ')') {
                res.push_back({c});
            } else {
                int j = i + 1;
                while (j < expression.size() && isdigit(expression[j])) j++;
                res.push_back(expression.substr(i, j - i));
                i = j - 1;
            }
        }
        return res;
    }

    vector<string> toReversePolishNotation(string& expression) {
        vector<string> res;
        stack<string> ops;
        vector<string> infixExpression = splitInfixExpression(expression);
        for (string& element: infixExpression) {
            if (isOperator(element)) {
                while (!ops.empty() && getPriority(ops.top()) > getPriority(element)) {
                    auto& op = ops.top(); ops.pop();
                    res.push_back(op);
                }
                ops.push(element);
            } else if (element == "(") {
                ops.push(element);
            } else if (element == ")") {
                while (ops.top() != "(") {
                    auto& op = ops.top(); ops.pop();
                    res.push_back(op);
                }
                ops.pop();
            } else {
                res.push_back(element);
            }
        }
        while (!ops.empty()) {
            if (ops.top() != "(") {
                res.push_back(ops.top());
                ops.pop();
            }
        }
        return res;
    }

    bool isOperator(string element) {
        return "+" == element || "-" == element || "*" == element || "/" == element;
    }

    int getPriority(string element) {
        if (element == "(") return 0;
        if (element == "+" || element == "-") return 1;
        if (element == "*" || element == "/") return 2;

        return -1;
    }

    int calculateReversePolishNotation(vector<string>& reversePolishExpression) {
        stack<int> st;
        for (string& element: reversePolishExpression) {
            if (isOperator(element)) {
                int num2 = st.top(); st.pop();
                int num1 = st.top(); st.pop();
                if (element == "+") st.push(num1 + num2);
                if (element == "-") st.push(num1 - num2);
                if (element == "*") st.push(num1 * num2);
                if (element == "/") st.push(num1 / num2);
            } else {
                st.push(stoi(element));
            }
        }
        return st.top();
    }
};


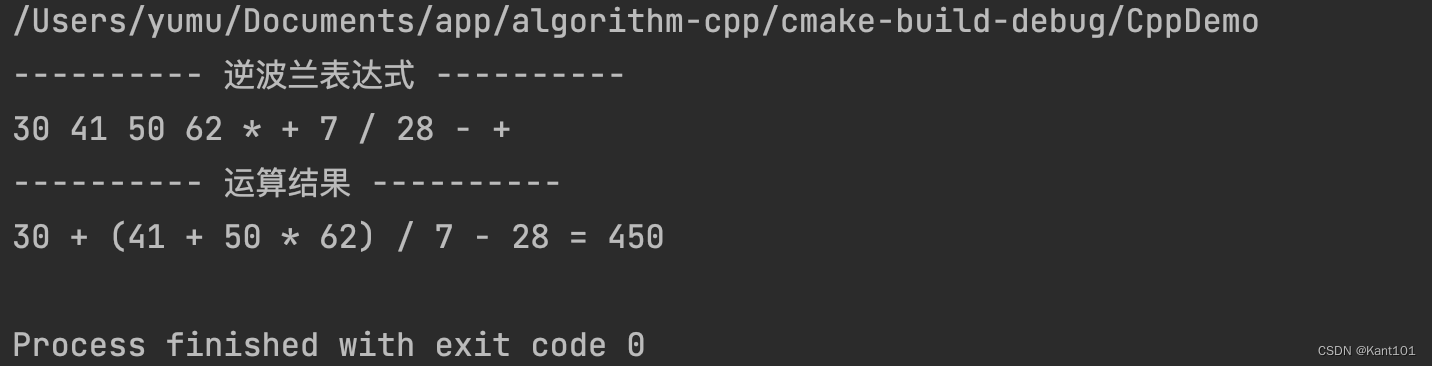
int main() {
    ReversePolishNotation reversePolishNotation;
    string expression = "30 + (41 + 50 * 62) / 7 - 28";
    vector<string> postFixExpression = reversePolishNotation.toReversePolishNotation(expression);
    cout << "---------- 逆波兰表达式 ----------" << endl;
    for (auto& element: postFixExpression) {
        cout << element << " ";
    }
    cout << endl;
    cout << "---------- 运算结果 ----------" << endl;
    int res = reversePolishNotation.calculateReversePolishNotation(postFixExpression);
    cout << expression << " = " << res << endl;
    return 0;
}

5. 参考文献

[1] https://www.cnblogs.com/relucent/p/15539448.html

# 算法 # 数据结构
Logo
DAMO开发者矩阵

DAMO开发者矩阵，由阿里巴巴达摩院和中国互联网协会联合发起，致力于探讨最前沿的技术趋势与应用成果，搭建高质量的交流与分享平台，推动技术创新与产业应用链接，围绕“人工智能与新型计算”构建开放共享的开发者生态。

更多推荐

cover

KingbaseES数据库：医疗信创潮涌沅江，国产化信创打造医疗新质生产力

avatar DAMO开发者矩阵
cover

告别迁移焦虑：金仓KDMS V4带你轻松搞定数据库国产化替代

avatar DAMO开发者矩阵
cover

KingbaseES数据库在常德二院全栈国产化信创中产生新质生产力,医疗信创的部署如何实现，如何操作？

avatar DAMO开发者矩阵