在时间序列分析中，如果存在某个时间点或时间段，这个点或时间段与前后数据的性质或统计特征明显不同，我们可以称其为“变点”（Changepoints）。变点可以表示时间序列中的结构性变化或趋势突变，通常用于检测时间序列中的非常规事件、异常、趋势变化或周期性变化。

Pelt（Pruned Exact Linear Time）是一种变点检测算法，用于发现时间序列数据中的结构性变化点或突变点。Pelt算法旨在查找最显著的变点，同时尽量减少计算成本。Pelt算法通常用于时间序列分析、金融数据分析、信号处理、生物信息学等领域，帮助识别数据中的关键结构性变化点。在金融领域，Pelt算法可以用于检测股票价格或其他金融时间序列中的市场崩溃、趋势变化等事件。
用Pelt法检测数据的趋势变化的Python代码如下：

# 导入ruptures库
# ruptures库需要单独安装，使用pip安装即可
import ruptures as rpt

# 选择"收盘价"列作为输入数据
input_data = df["收盘"].values

# 创建ruptures模型
model = "l2"  # 选择使用的模型
algo = rpt.Pelt(model=model).fit(input_data)

# 检测断点
result = algo.predict(pen=30)

# 绘制变点检测结果
plt.figure(dpi=300)
plt.plot(df.index, input_data, label="收盘价", color="b")
for change_point in result:
    if change_point < len(input_data):  # 确保变点在合法的索引范围内
        plt.axvline(df.index[change_point], color="r", linestyle="--", label="变点")
plt.title("Pelt变点检测")
plt.xlabel("日期")
plt.ylabel("收盘价")
plt.legend()
plt.show()

运行代码，会得到下图所示的结果：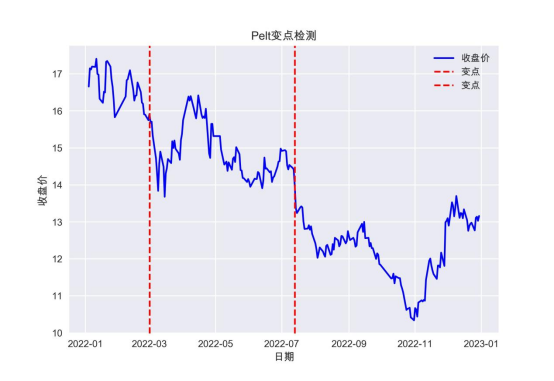

Pelt算法通常需要用户指定一个模型，以描述时间序列的性质。不同的应用领域可能需要不同的模型。这里我们指定的模型是“L2”，是指使用L2范数（欧几里德范数）来度量模型的拟合质量。在时间序列分析中，L2模型通常用于表示数据点之间的差异的平方和。

在Pelt算法的上下文中，L2模型的目标是最小化变点处的拟合误差的平方和。它假设数据点在每个分段（在两个变点之间）上都是独立同分布的，而每个分段可以用一个简单的模型来描述。这个简单模型通常是一个均值，表示在该分段中数据点的平均值。

Pelt算法使用L2模型时，通过寻找最优的变点配置，以最小化数据点与各自分段模型的拟合误差的平方和。因此，L2模型是一种用于时间序列分析中的常见模型之一，适用于各种应用领域，包括金融数据分析和信号处理等。

此外，Pelt算法的目标是找到一个变点配置，使成本函数的总值最小。这个总成本包括变点处的成本以及模型选择的代价。算法还会考虑一个惩罚项（penalty），以平衡变点数量和质量。这里我们设置参数“pen=30”设定了惩罚项，在这个设置下，Pelt算法在行情数据中找到了2处变点。从图4-3中可以看到，这2处变点都处在股价极速下跌过程中，也就是说股价进入了更加明显的下跌趋势。读者可以自行修改pen参数的数值，观察结果的变化。

参考书目：

北京大学出版社

《巧用AI大模型轻松学会Python金融数据分析》