一 树的定义

树（Tree）**是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中： 1）有且仅有一个特定的称为根（Root）的结点； 2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、…、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
1）根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）子树的个数没有限制，但它们一定是互不相交的。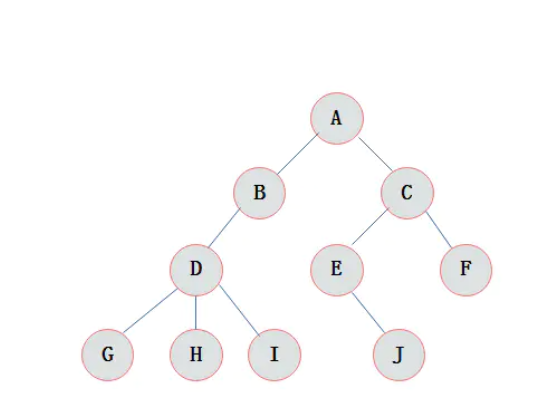

二 特殊名词的解释

1.度数：结点拥有的子树数目称为结点的度。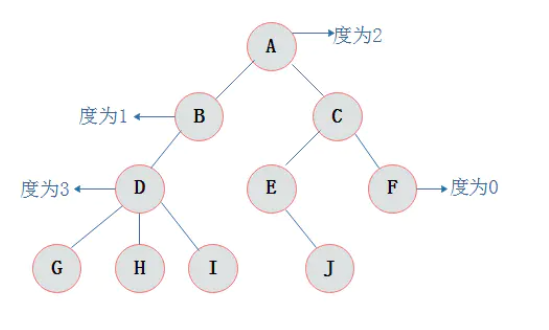

2. 节点关系
孩子节点：结点的子树的根称为该结点的孩子；
兄弟节点：同一双亲的孩子结点； 堂兄结点：同一层上结点；
双亲节点：B 结点是A 结点的孩子，则A结点是B 结点的双亲；（可以理解为父亲节点）
叶子节点：度位零的节点。
3.层次：从根节点开始定义起，根为第一层，根的孩子为第二层，以此类推。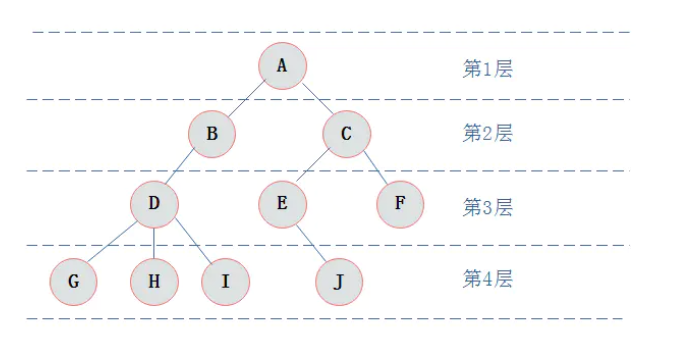

4.深度 ：树中结点的最大层次，如上图深度为4

三 二叉树（重点知识）

1.定义：二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。 如图为普通二叉树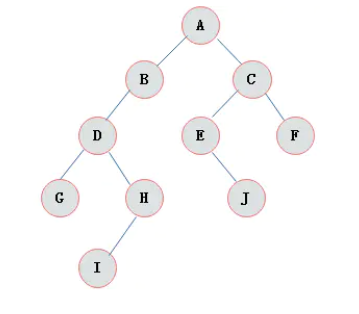

特点
不存在度超过2点节点
左右子树是有序的。
性质
1.第i层上最多有 2^i-1 个节点 。
2.如果深度为k,最多有2^k-1个节点。(k>=1。
3.叶子节点数=度为2的节点+1。（用最后一层为满的去推导）
4.在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5.若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下。
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子结点， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点
满二叉树
在一棵二叉树中。如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。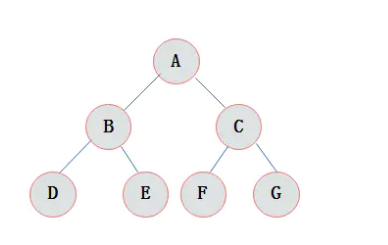

特点
叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
非叶子结点的度一定是2。
在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。
完全二叉树
定义：若设二叉树的深度为h，除第 h 层外，其它各层 (1~h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（就是说除最后一层外 其他层都是满的 且最后一层节点只能集中在左侧）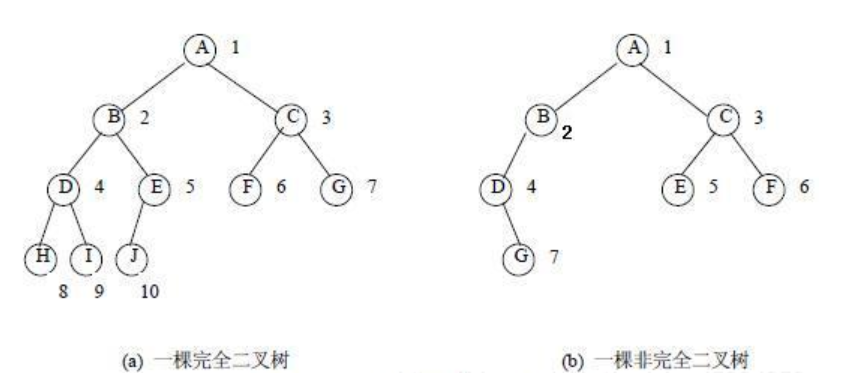

总结

树作为一种基础的数据结构，被严谨地定义为 n（n≥0）个结点的有限集。当 n = 0 时，此为一棵空树，它就像一个尚未被开垦的数据容器，不包含任何实际的数据元素。而一旦 n > 0，树便有了实质内容，其中有且仅有一个结点被赋予特殊地位，即根结点，它宛如家族中的始祖，是整棵树层级结构的起始点。其余结点则依据特定规则，可被清晰地划分为 m（m > 0）个互不相交的有限集 T1、T2、…、Tm ，并且这些集合中的每一个自身又构成一棵树，被称作根的子树，恰似家族繁衍出的不同分支家族。
在树的结构体系里，一系列与之相关的概念进一步丰富了我们对其理解的维度。度数，用来精准衡量每个结点所拥有的子树数目，通过度数，我们能直观判断某个结点在树中的分支能力，度数高的结点就如同交通枢纽，连接着众多路径。孩子节点，是结点子树的根，形象地描绘了结点间的亲子关系；兄弟节点，代表着同一双亲下的孩子，就像现实家庭中的兄弟姐妹；堂兄结点，指的是处于同一层上的结点，反映了树结构中层级间的横向关联；双亲节点与孩子节点相对，若 B 结点是 A 结点的孩子，那么 A 结点就是 B 结点的双亲，这种关系奠定了树结构中节点间回溯查找的基础；叶子节点，作为度为零的节点，它们处在树的末端，恰似家族中不再有分支后代的个体。此外，层次从根节点开始计数，根为第一层，根的孩子为第二层，以此类推，清晰地刻画了节点在树中的纵向位置；深度则是树中结点的最大层次，体现了树的纵向延展程度。
二叉树作为树结构中尤为重要的一个分支，有着独特的定义与性质。它同样是 n（n≥0）个结点的有限集合，这个集合要么为空集，形成空二叉树，要么由一个根结点以及两棵互不相交的左子树和右子树组成，这两棵子树分别占据着根结点的左右两侧，且顺序严格不可随意调换。二叉树具有诸多关键性质：在层级分布上，第 i 层上最多存在 2^(i - 1) 个节点，这是基于其二叉分支特性推导得出的数学规律；若考虑整棵二叉树的深度为 k，那么其最多可容纳 2^k - 1 个节点（k≥1），该性质对于预估二叉树存储容量至关重要；在节点数量关系上，叶子节点数与度为 2 的节点数存在着叶子节点数 = 度为 2 的节点数 + 1 的奇妙等式关系，这一关系在许多涉及二叉树节点数量计算的场景中广泛应用；在完全二叉树情境下，若其拥有 n 个节点，深度为 [log₂n] + 1（[log₂n] 为向下取整），并且对含 n 个结点的完全二叉树按特定顺序编号后，每个编号为 i 的结点都遵循明确规则，如 i = 1 时该结点为根无双亲，否则编号为 [i/2] 的结点是其双亲；若 2i > n 则无左孩子，否则编号 2i 的结点为左孩子；若 2i + 1 > n 则无右孩子，否则编号 2i + 1 的结点为右孩子，这些规则为完全二叉树在存储和遍历等操作上提供了极大便利。
在二叉树的范畴内，满二叉树和完全二叉树是两种特殊且具有代表性的类型。满二叉树，结构上极为规整，所有分支结点都同时存在左子树和右子树，并且所有叶子结点都整齐地排列在同一层上。这使得满二叉树在叶子分布和分支特性上表现出高度一致性，叶子只能出现在最下一层，若出现在其他层则无法满足其严格的平衡定义，同时非叶子结点的度必定为 2，在同样深度的二叉树中，满二叉树的结点个数最多，叶子数也最多，这种特性使其在一些对结构对称性和数据均匀分布有要求的场景中具有独特优势。完全二叉树，在结构上有自身特点，若设其深度为 h，除第 h 层外，其它各层（1 ~ h - 1）的结点数都达到该层能容纳的最大个数，而第 h 层所有的结点都连续集中在最左边。它既保留了满二叉树大部分层次结构饱满的特性，又在最后一层展现出一定的灵活性，这种结构在很多实际应用中，尤其是在需要兼顾空间利用和数据操作效率的场景里，发挥着重要作用。

思考

树和二叉树在众多实际场景中扮演着举足轻重的角色。在计算机科学领域，文件系统目录结构堪称树结构的经典应用实例。磁盘中不同盘符下的多层文件夹嵌套，恰似一棵枝繁叶茂的大树，根结点如同磁盘盘符，各级文件夹如同树中的分支结点，而文件则是叶子节点。通过树结构，用户能够清晰直观地理解文件系统的层级逻辑，方便快捷地进行文件与文件夹的管理操作，无论是文件的查找、移动还是删除，树结构都能提供高效的路径指引。
二叉树凭借自身独特的结构特性，在搜索算法方面展现出卓越的性能优势。二叉搜索树作为二叉树的一种变体，充分利用了二叉树节点有序排列的特点，使得数据查找操作能够以对数时间复杂度完成。在数据库索引构建过程中，二叉搜索树的这种高效查找特性被广泛应用。数据库中存储着海量的数据记录，为了实现快速检索特定数据，常采用二叉搜索树结构构建索引。当用户执行查询操作时，系统能够依据二叉搜索树的查找规则，迅速定位到目标数据所在位置，大大缩短了数据检索时间，提升了数据库系统的整体响应速度和查询效率。
满二叉树与完全二叉树的特殊性质为数据存储优化提供了极具价值的思路。以完全二叉树为例，在数组存储方式中，由于其节点编号具有特定规律，可利用这种规律实现节点在数组中的紧凑存储，有效节省存储空间。在堆排序算法里，完全二叉树特性得到巧妙运用。堆本质上是一种特殊的完全二叉树，通过维护堆的性质，能够高效地完成数据排序操作，在时间复杂度和空间复杂度上都取得了较好的平衡，极大提升了排序效率，适用于对大量数据进行排序的场景。
在编译原理领域，语法树常以二叉树的形式构建。编译器在对源程序进行语法分析时，会根据语法规则将程序语句转化为一棵二叉树结构。树中的每个节点代表一个语法单元，通过对这棵语法树的遍历和分析，编译器能够准确理解程序的语法结构，检查语法错误，并进一步将源程序转化为目标代码，确保程序能够正确编译和运行。
在地理信息系统（GIS）中，四叉树作为二叉树的一种变体，发挥着重要作用。GIS 需要处理和存储大量的地理空间数据，如地图中的地形、地物分布等信息。四叉树结构能够将地理空间递归地划分为四个象限，每个象限再进一步细分，以此实现对地理空间数据的高效存储和检索。通过四叉树，能够快速定位到特定地理区域内的数据，大大提高了地理信息查询和分析的效率，满足了 GIS 在地图显示、空间分析等方面对数据处理速度的严格要求。
深入思考如何依据不同业务需求，巧妙选择并定制合适的树结构，已然成为提升系统性能、高效处理数据的核心关键。不同的业务场景对数据的组织、存储和操作有着各异的要求，只有精准把握树和二叉树的各种特性，结合具体业务逻辑，才能设计出最优的数据结构方案。这一过程不仅能够显著提升系统在数据处理方面的效率，还将促使我们对数据结构底层原理形成更为深刻的认知与运用能力。例如在面对海量数据存储与快速检索的复杂场景时，合理设计树结构，包括选择合适的树类型、优化节点分布和层级关系等，能够大幅提升系统的响应速度，确保在短时间内准确获取所需数据，为业务的高效运行提供坚实保障。