一句话提要

VASPKIT v1.00可以批量生成施加应变以后的结构，并根据能量-应变关系求解弹性常数矩阵。

计算能带反折叠—VASPKIT v1.00新功能

计算跃迁电偶极矩—VASPKIT v1.00新功能

深入分析能带结构(二)-VASPKIT能带图计算

VASPKIT计算电荷密度差

在材料的线性形变范围内(应变较小的情况下)，体系的应力与应变满足胡克定律，

其中 σ 和 ε 分别表示应力和应变，Cij是弹性刚度常数，这里 1 ≤ i ≤ 6 即应变和应力分别有6个独立分量。施加应变后体系的应变能可按应变张量 ε 进行泰勒级数展开并取二阶近似得到：

这里E(V, ε)和E(V0, 0)别表示施加应变后和基态构型的总能，V0是平衡体积。

因此，采用第一性原理计算弹性常数有两种方法，第一种方法是应力-应变方法，即通过给结构施加不同应变，分别计算出所对应的应力大小，然后利用公式(1)拟合得到一次项系数，从而得到Cij。第二种方法是能量-应变方法，即通过给结构施加不同应变后计算出体系总能相对于基态能量变化(应变能)，再利用公式(2)进行二次多项式拟合，其中二次多项式系数是晶体的某个弹性常数或者弹性常数组合。第一种方法优点是每进行一次计算可一次得到 σ 六个独立分量，缺点是为了得到准确的应力大小，必须选择更高的截断能和更密集的K格点。在同样的精度下，能量-应变法相比应力-应变方法要求的截断能和K点数目相对较少，缺点是计算应变数目有所增加。VASPKIT中弹性常数计算基于能量-应变法，目前不支持三斜晶系。

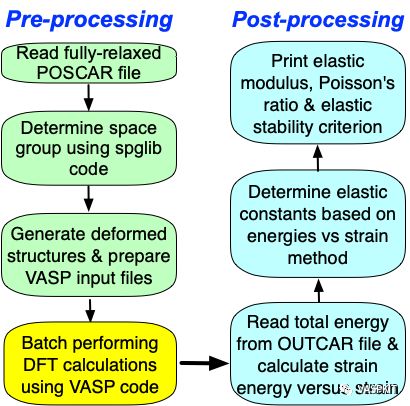
VASP+VASPKIT基于能量-应变法计算晶体弹性常数及力学性质

这里我们以金刚石结构为例讲解如何采用能量-应变函数关系计算弹性常数，详见vaspkit/examples/elastic/diamond_3D。对于金刚石立方结构，一共有3个独立弹性常数C11, C12 和 C44。

立方晶系的弹性能可以表示：

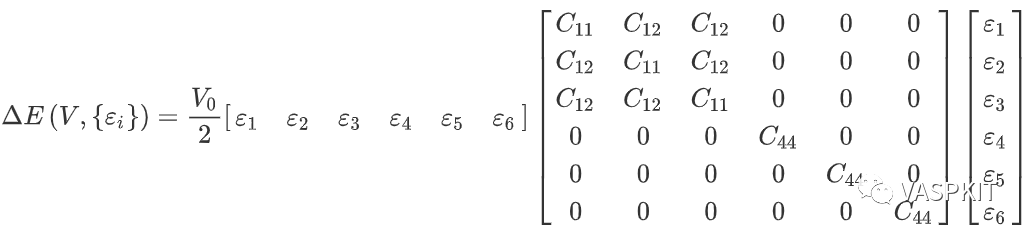
VASPKIT和VASP计算晶体的弹性常数具体计算步骤分为：

1，准备优化彻底的POSCAR文件，注意通常采用标准的惯用原胞计算弹性常数，如果不确信POSCAR文件中是否是标准的惯用原胞，可以用vaspkit-603/604生成标准结构；

2，运行vaspkit 选择102生成KPOINTS，由于计算弹性常数对K-mesh要求很高，因此对于半导体(金属体)体系，生成K点的精度应不小于0.03(0.02) * 2π Å-1

3，INCAR参考设置如下；

Global Parameters  ISTART =  0          LREAL  =  F        PREC   =  High  (截断能设置默认值1.5-2倍)  LWAVE  = F        LCHARG = F      ADDGRID= .TRUE.    Electronic Relaxation  ISMEAR =  0            SIGMA  =  0.05        NELM   =  40            NELMIN =  4            EDIFF  =  1E-08      Ionic Relaxation  NELMIN =  6            NSW    =  100          IBRION =  2            ISIF   =  2    (切记选择2,如果选择3会把施加应变后原胞重新优化成平衡原胞)  EDIFFG = -1E-02  

4，准备VPKIT.in文件并设置第一行为1(预处理)；运行vaspkit并选择201, 将生成用于计算弹性常数文件；

1                    ! 设置1将产生计算弹性常数的输入文件，2则计算弹性常数3D                   ! 2D为二维体系，3D为三维体系7                    ! 7个应变-0.015 -0.010 -0.005 0.000 0.005 0.010 0.015  ! 应变变化范围

运行vaspkit后输出一下信息

 ------------>>201  -->> (01) Reading VPKIT.in File... +-------------------------- Warm Tips --------------------------+      See an example in vaspkit/examples/elastic/diamond_3D,   Require the fully-relaxed and standardized Convertional cell. +---------------------------------------------------------------+  -->> (02) Reading Structural Parameters from POSCAR File...   -> C44 folder created successfully!   -> strain_-0.015 folder created successfully!   -> strain_-0.010 folder created successfully!   -> strain_-0.005 folder created successfully!   -> strain_0.000 folder created successfully!   -> strain_+0.005 folder created successfully!   -> strain_+0.010 folder created successfully!   -> strain_+0.015 folder created successfully!   -> C11_C12_I folder created successfully!   -> strain_-0.015 folder created successfully!   -> strain_-0.010 folder created successfully!   -> strain_-0.005 folder created successfully!   -> strain_0.000 folder created successfully!   -> strain_+0.005 folder created successfully!   -> strain_+0.010 folder created successfully!   -> strain_+0.015 folder created successfully!   -> C11_C12_II folder created successfully!   -> strain_-0.015 folder created successfully!   -> strain_-0.010 folder created successfully!   -> strain_-0.005 folder created successfully!   -> strain_0.000 folder created successfully!   -> strain_+0.005 folder created successfully!   -> strain_+0.010 folder created successfully!   -> strain_+0.015 folder created successfully!

5，批量提交vasp作业；

6，再次修改VPKIT.in文件中第一行为2(后处理)，然后再次运行vaspkit并选择201，得到以下结果；

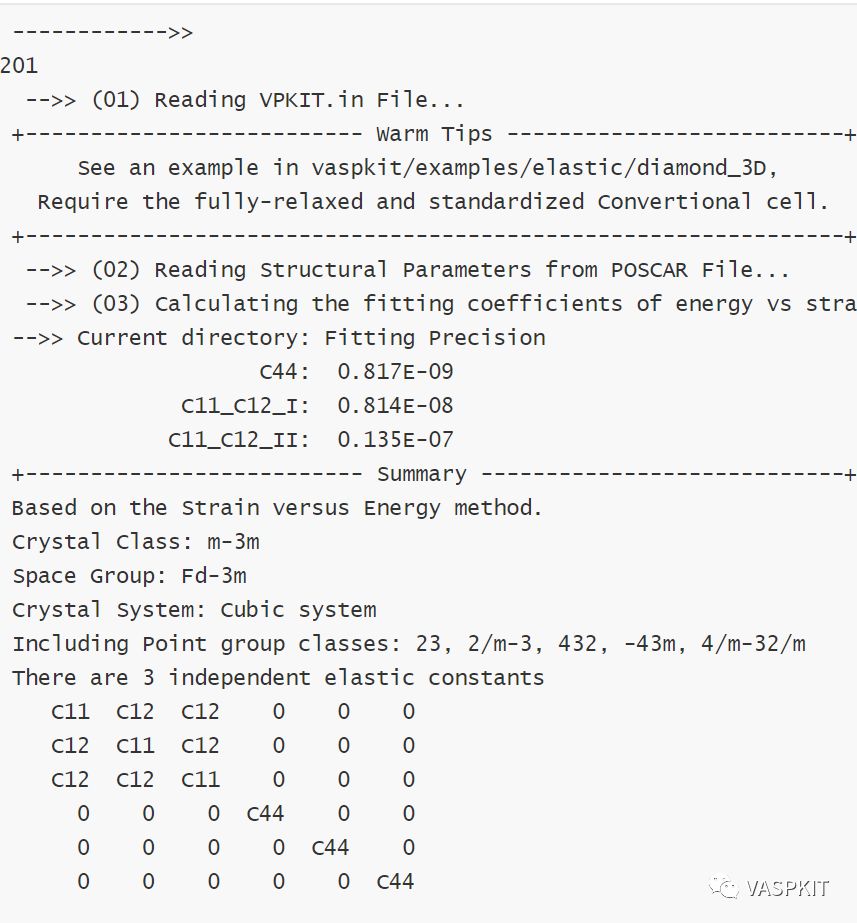
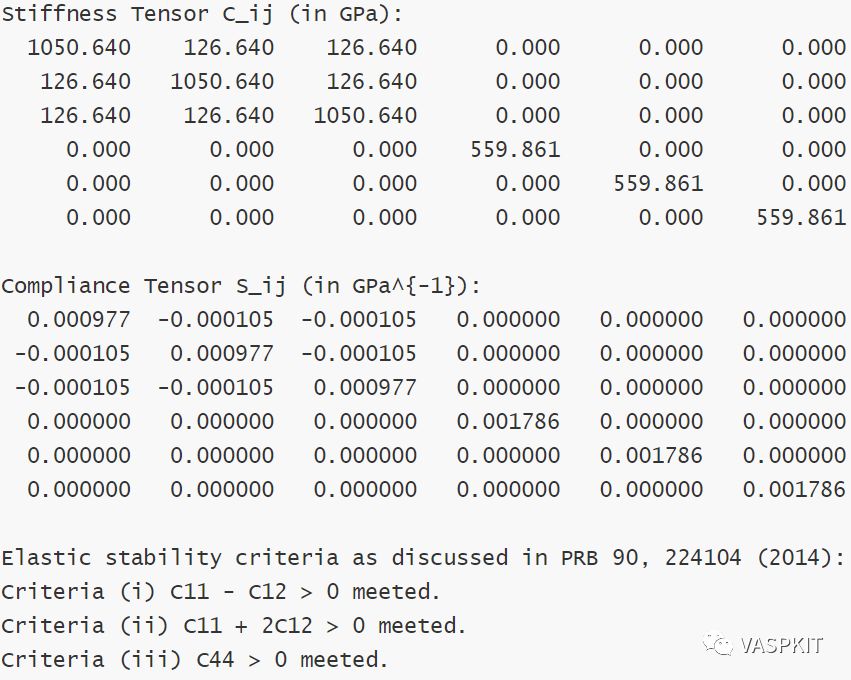
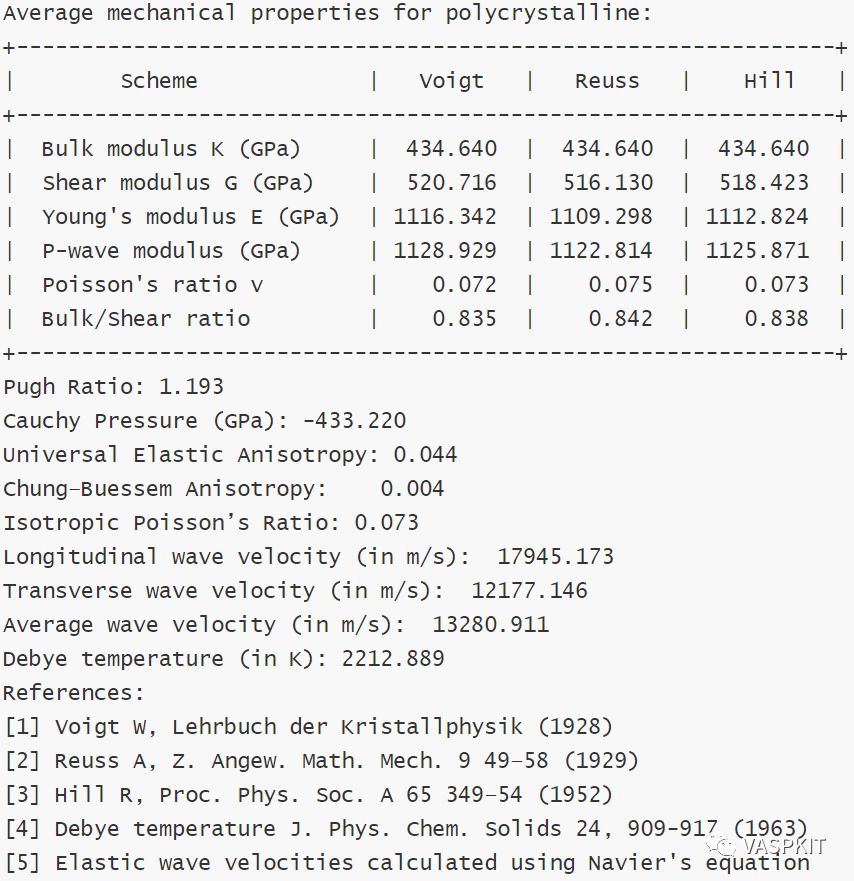
金刚石弹性常数实验值分别为：C11 = 1079 GPa, C12 = 124 GPa 和 C44 = 578 GPa [3],通过比较发现采用VASPKIT结合VASP得到的理论计算弹性常数与实验值符合较好。另外，最新版本也支持从OUTCAR或ELASTIC_TENSOR.in文件中读取弹性常数，计算各种力学性质，见vaspkit/examples/elastic。

参考文献：

[1] 武松，利用 VASP 计算不同晶系晶体弹性常数

[2] 侯柱锋，采用VASP如何计算晶体的弹性常数

[3] McSkimin H J and Andreatch P 1972 J. Appl. Phys. 43 2944