基于粒子群算法(PSO)的寻优计算
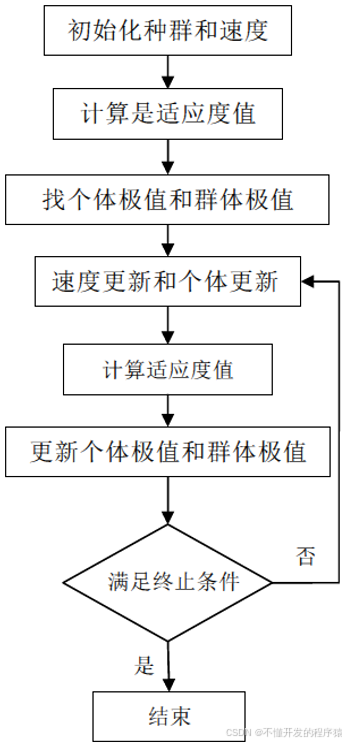
粒子群算法(PSO)是一种基于群体的随机优化技术。与其它基于群体的进化算法相比,它们均初始化为一组随机解,通过迭代搜寻最优解。不同的是:进化计算遵循适者生存原则,而PSO模拟社会。将每个可能产生的解表述为群中的一个微粒,每个微粒都具有自己的位置向量和速度向量,以及一个由目标函数决定的适应度。所有微粒在搜索空间中以一定速度飞行,通过追随当前搜索到的最优值来寻找全局最优值。PSO模拟社会采用了以下三条
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计3077字,阅读大概需要10分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿❗❗❗知识付费,🈲止白嫖,有需要请后台私信或【文末】个人微信公众号联系我
基于粒子群算法(PSO)的寻优计算
1. 基本粒子群算法
粒子群算法(PSO)是一种基于群体的随机优化技术。与其它基于群体的进化算法相比,它们均初始化为一组随机解,通过迭代搜寻最优解。不同的是:进化计算遵循适者生存原则,而PSO模拟社会。将每个可能产生的解表述为群中的一个微粒,每个微粒都具有自己的位置向量和速度向量,以及一个由目标函数决定的适应度。所有微粒在搜索空间中以一定速度飞行,通过追随当前搜索到的最优值来寻找全局最优值。
PSO模拟社会采用了以下三条简单规则对粒子个体进行操作:①飞离最近的个体,以避免碰撞。②飞向目标。③飞向群体的中心。这是粒子群算法的基本概念之一。
粒子群算法其基本思想是受许多鸟类的群体行为进行建模与仿真研究结果的启发。
Frank Heppner的鸟类模型在反映群体行为方面与其它类模型有许多相同之处。由于鸟类用简单的规则确定自己的飞行方向与飞行速度(实质上,每只鸟都试图停在鸟群中而又不相互碰撞),当一只鸟飞离鸟群而飞向栖息地时,将导致它周围的其他鸟也飞向栖息地。这些鸟一旦发现栖息地,将降落在此,驱使更多的鸟落在栖息地,直到整个鸟群都落在栖息地。
粒子群算法与其它的进化类算法类似,也采用“群体”和“进化”的概念,同样也根据个体的适应值大小进行操作。不同的是,PSO中没有进化算子,而是将每个个体看作搜索空间中没有重量和体积的微粒,并在搜索空间中以一定的速度飞行,该飞行速度由个体飞行经验和群体的飞行经验进行动态调整。

PSO算法流程如图所示
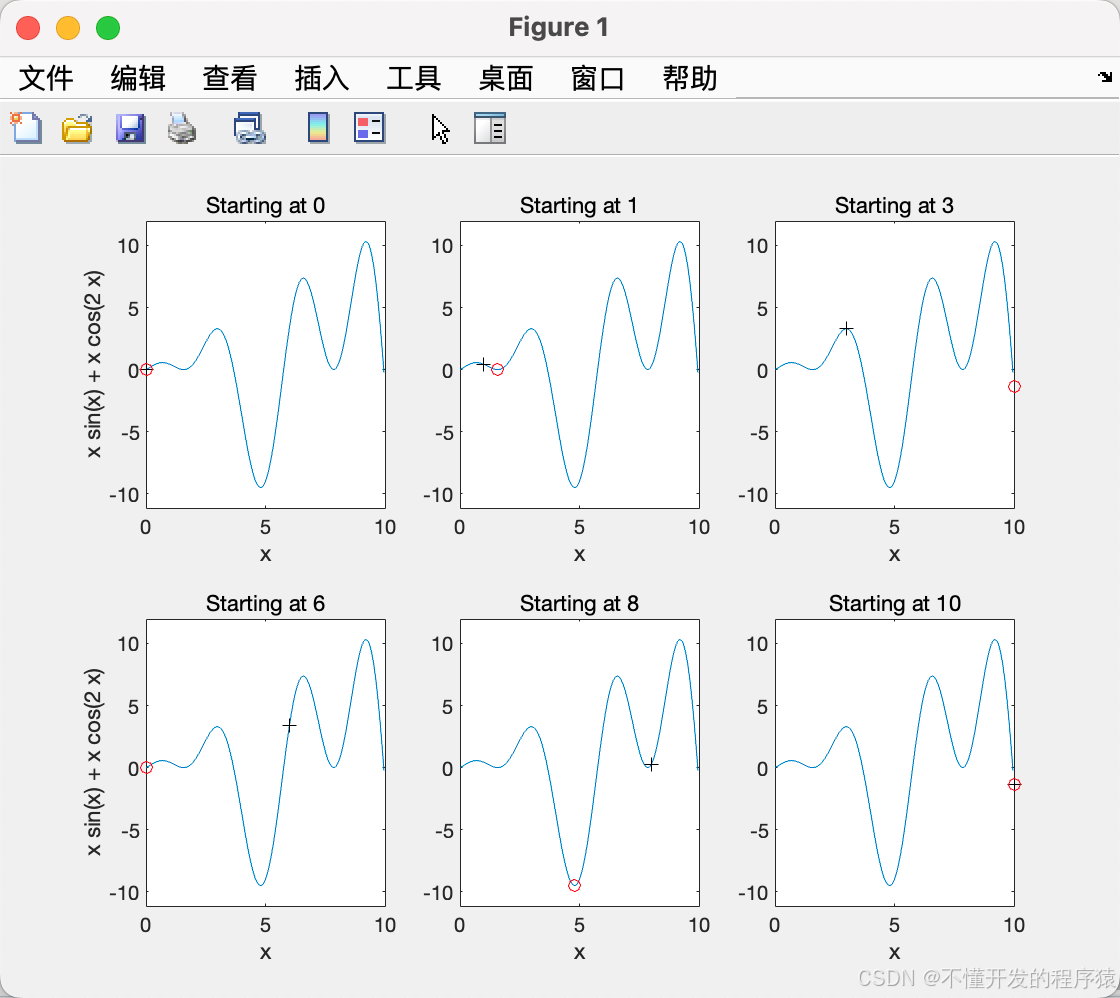
采用fmincon进行有约束的非线性最小化求解
f ( x ) = x s i n ( x ) + x / c o s ( x ) f(x)=xsin(x)+x/cos(x) f(x)=xsin(x)+x/cos(x)
%% 1维函数,全局最小寻优
% finding the mimimum value.
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
%% 目标方程
f = @(x) x.*sin(x) + x.*cos(2.*x);
%% 边界
lb = 0; % 下限
ub = 10; % 上限
%% 找最小值 + 画图
x0 = [0 1 3 6 8 10];
hf = figure;
for i=1:6
% fmincon:求多个变量的目标函数的最小值
% fmincon(FUN,X,A,B,Aeq,Beq,LB,UB,NONLCON,options,varargin)
x(i) = fmincon(f,x0(i),[],[],[],[],lb,ub,[],...
optimset('Algorithm','SQP','Disp','none'));
subplot(2,3,i)
ezplot(f,[lb ub]);
hold on
plot(x0(i),f(x0(i)),'k+')
plot(x(i),f(x(i)),'ro')
hold off
title(['Starting at ',num2str(x0(i))]) %起始点
if i == 1 || i == 4
ylabel('x sin(x) + x cos(2 x)')
end
end
%% A common GOTCHA!
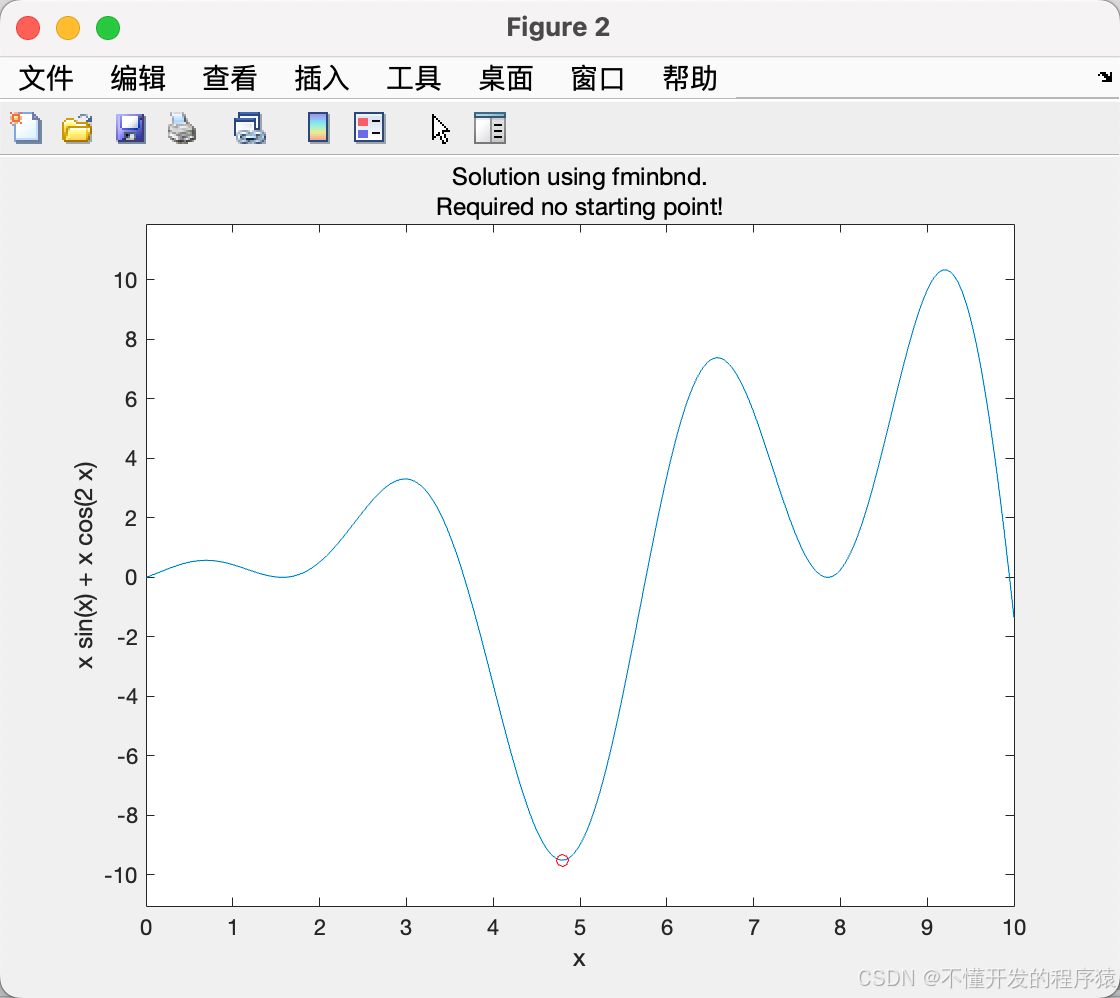
% 一维边界最小值问题 --- Solver: |fminbnd|.
x2 = fminbnd(f,lb,ub)% 单变量边界非线性函数最小求解
figure
ezplot(f,[lb ub]);
hold on
plot(x2,f(x2),'ro')
hold off
ylabel('x sin(x) + x cos(2 x)')
title({'Solution using fminbnd.','Required no starting point!'})
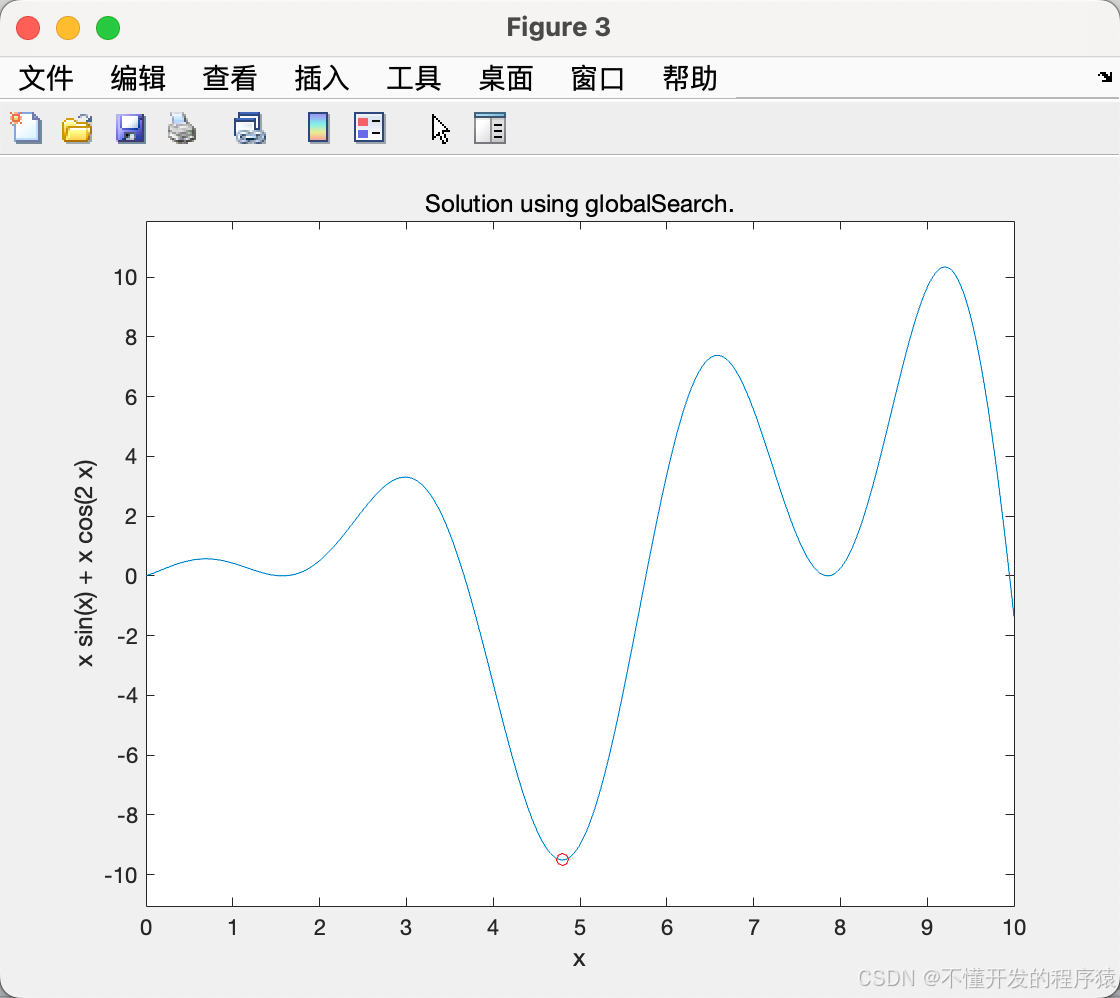
%% 使用globalSearch or MultiStart寻优
problem = createOptimProblem('fmincon','objective',f,'x0',x0(1),'lb',lb,...
'ub',ub,'options',optimset('Algorithm','SQP','Disp','none'));
gs = GlobalSearch; % 全局寻优
xgs = run(gs,problem); % 执行当前路径 --> Use CD or ADDPATH to make the script executable from the prompt
figure,
ezplot(f,[lb ub]);
hold on
plot(xgs,f(xgs),'ro')
hold off
ylabel('x sin(x) + x cos(2 x)')
title('Solution using globalSearch.')
2. 经典测试函数
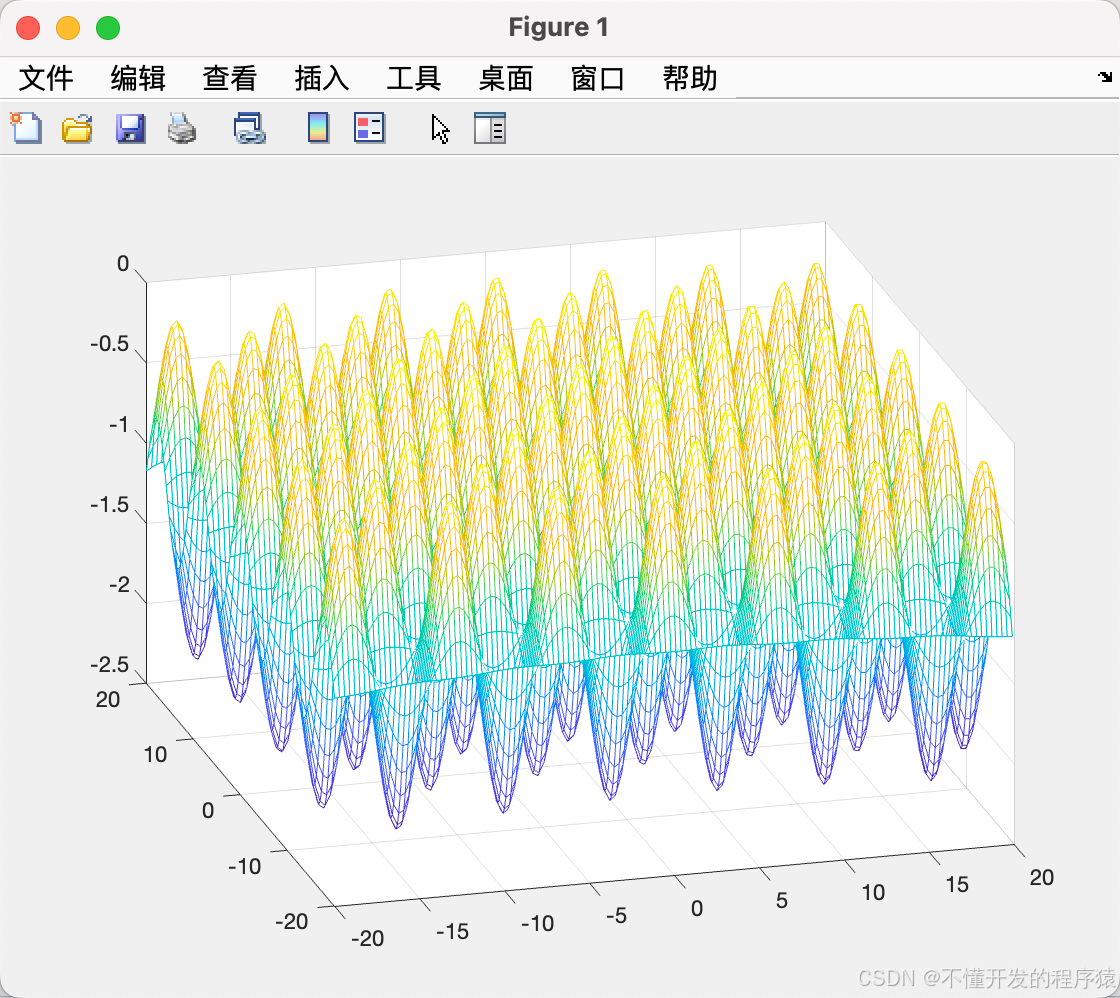
2.1 Griewank函数
% %% 经典测试函数
% % finding the mimimum value.
% clc % 清屏
% clear all; % 删除workplace变量
% close all; % 关掉显示图形窗口
function y10_4
% 绘制Griewank函数图形
x = [-20 : 0.3 : 20];
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Griewank([X(h,l),Y(h,l)]);
end
end
mesh(X,Y,z);
view([-15.5 30]);
shading interp
end
function y=Griewank(x)
% Griewan函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y1 = 1 / 4000 * sum(x.^2 );
y2 = 1 ;
for h = 1 :col
y2 = y2 * cos(x(h) / sqrt(h));
end
y = y1 - y2 + 1 ;
y =- y;
end
2.2 Rastrigin函数
% %% 经典测试函数
% % finding the mimimum value.
% clc % 清屏
% clear all; % 删除workplace变量
% close all; % 关掉显示图形窗口
function DrawRastrigin()
% 绘制Rastrigin函数图形
x = [-5 : 0.05 : 5 ];
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
end
end
mesh(X,Y,z);
shading interp
end
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y = sum(x.^2 - 10 * cos( 2 * pi * x) + 10 );
y =y;
end
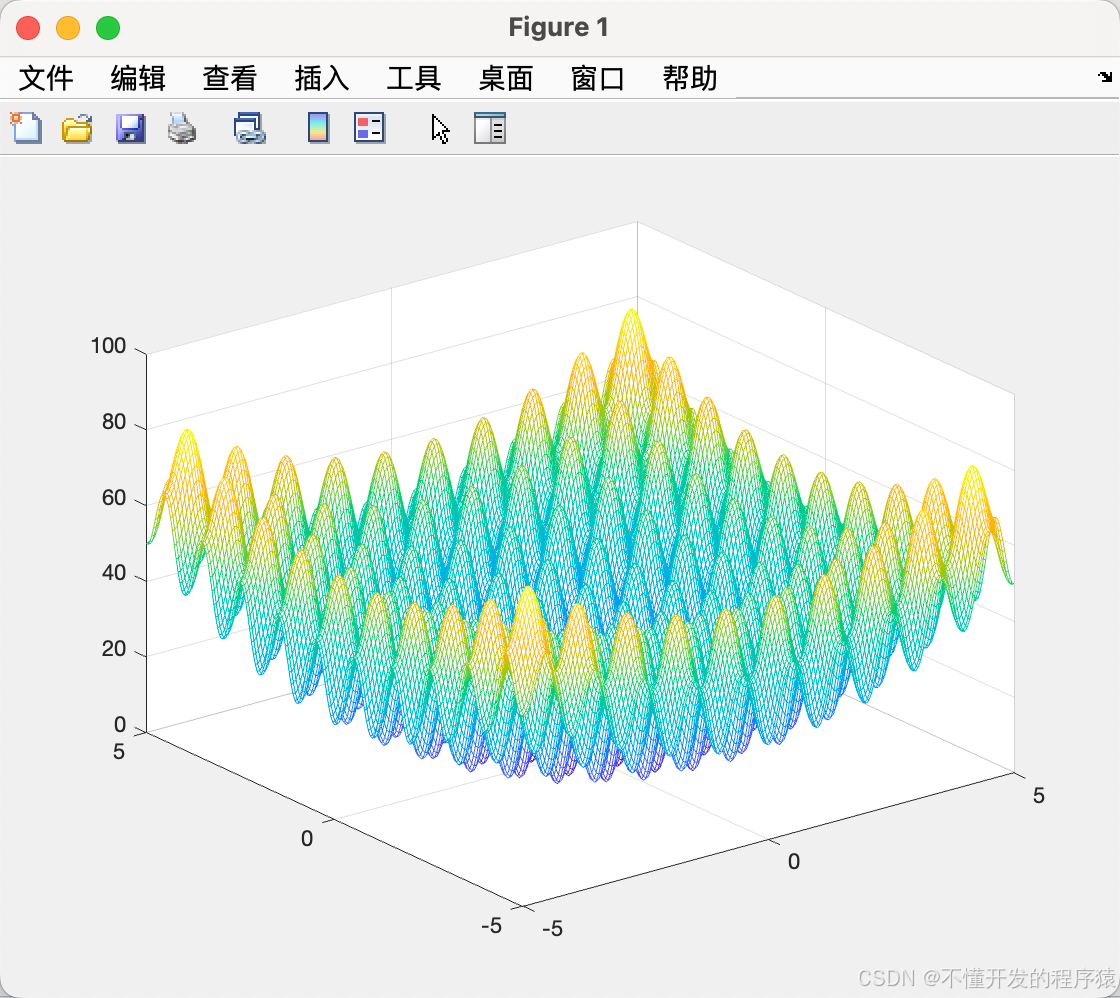
2.3 Schaffer函数
function DrawSchaffer()
x=[-5:0.05:5];
y=x;
[X,Y]=meshgrid(x,y);
[row,col]=size(X);
for l=1:col
for h=1:row
z(h,l)=Schaffer([X(h,l),Y(h,l)]);
end
end
mesh(X,Y,z);
shading interp
end
function result=Schaffer(x1)
%Schaffer函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极大点1.
[row,col]=size(x1);
if row>1
error('输入的参数错误');
end
x=x1(1,1);
y=x1(1,2);
temp=x^2+y^2;
result=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
end
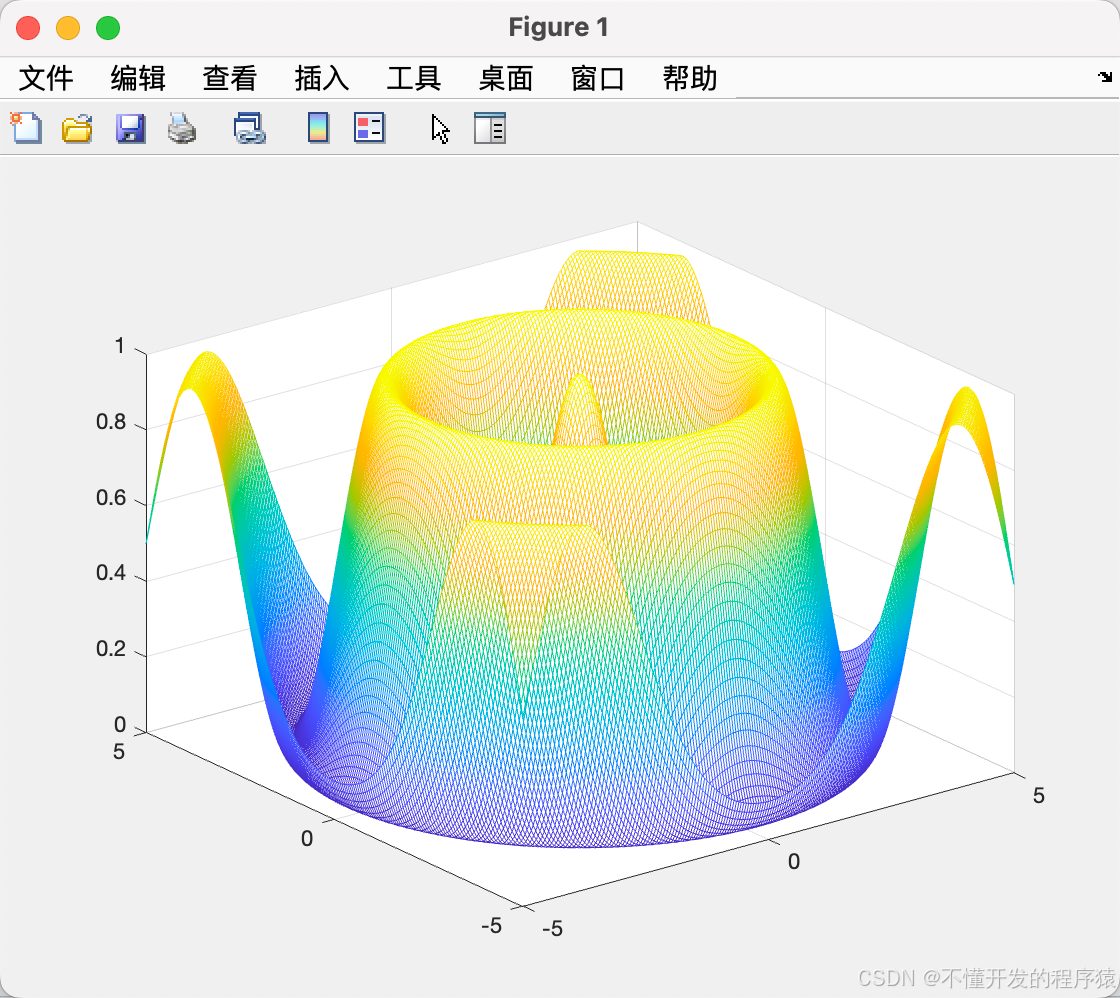
2.4 Ackley函数
function DrawAckley()
%绘制Ackley函数图形
x=[-8:0.1:8];
y=x;
[X,Y]=meshgrid(x,y);
[row,col]=size(X);
for l=1:col
for h=1:row
z(h,l)=Ackley([X(h,l),Y(h,l)]);
end
end
mesh(X,Y,z);
shading interp
end
function y=Ackley(x)
%Ackley?函数??
%输入x,给出相应的y值,在x=(0,0,…,0)?处有全局极小点0,为得到最大值,返回值取相反数??
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y=-20*exp(-0.2*sqrt((1/col)*(sum(x.^2))))-exp((1/col)*sum(cos(2*pi.*x)))+exp(1)+20;
end
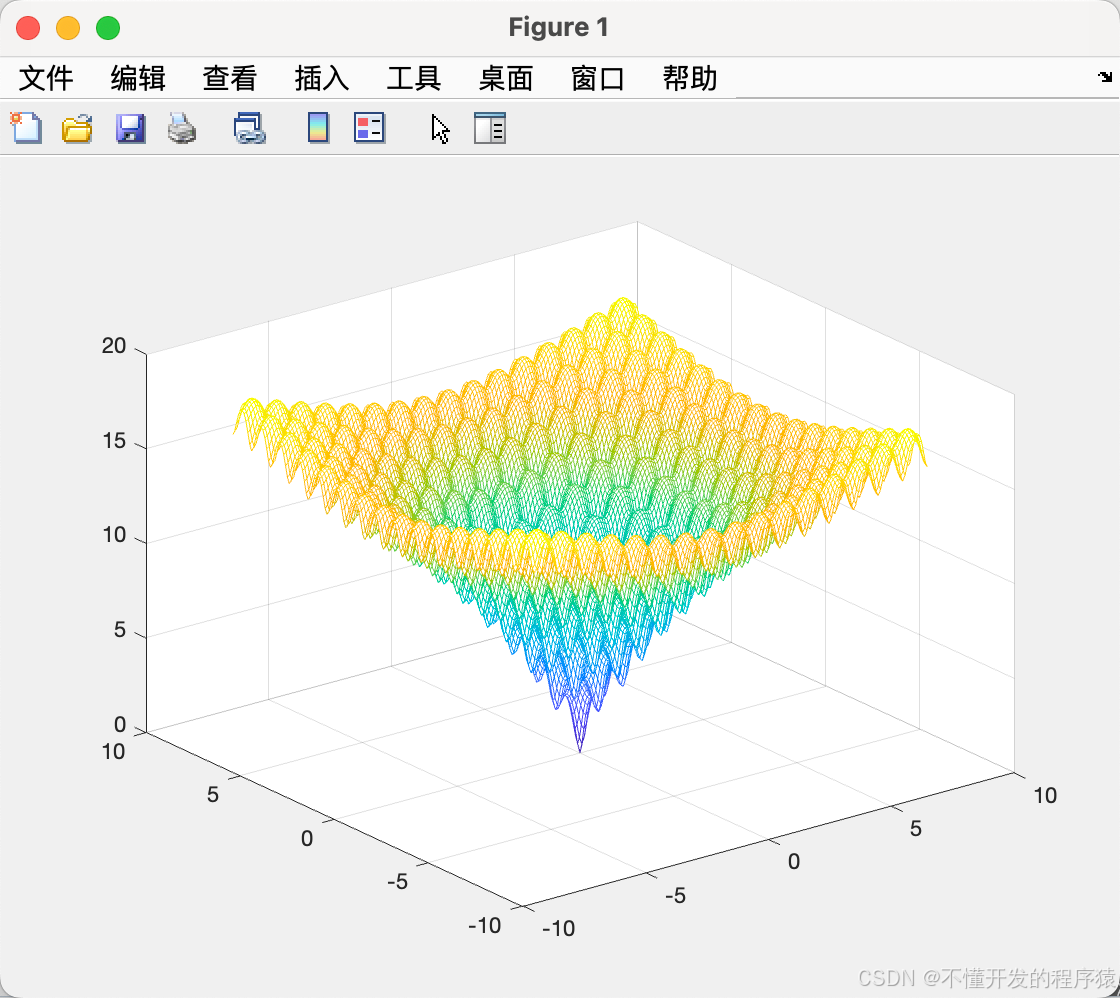
2.5 Rosenbrock函数
function DrawRosenbrock()
%绘制Rosenbrock函数图形
x=[-8:0.1:8];
y=x;
[X,Y]=meshgrid(x,y);
[row,col]=size(X);
for l=1:col
for h=1:row
z(h,l)=Rosenbrock([X(h,l),Y(h,l)]);
end
end
mesh(X,Y,z);
shading interp
end
function y=Rosenbrock(x)
%Rosenbrock 函数
%输入x,给出相应的y值,在x=(1,1,…,1) 处有全局极小点0,为得到最大值,返回值取相反数
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y=100*(x(1,2)-x(1,1)^2)^2+(x(1,1)-1)^2;
y=-y;
end
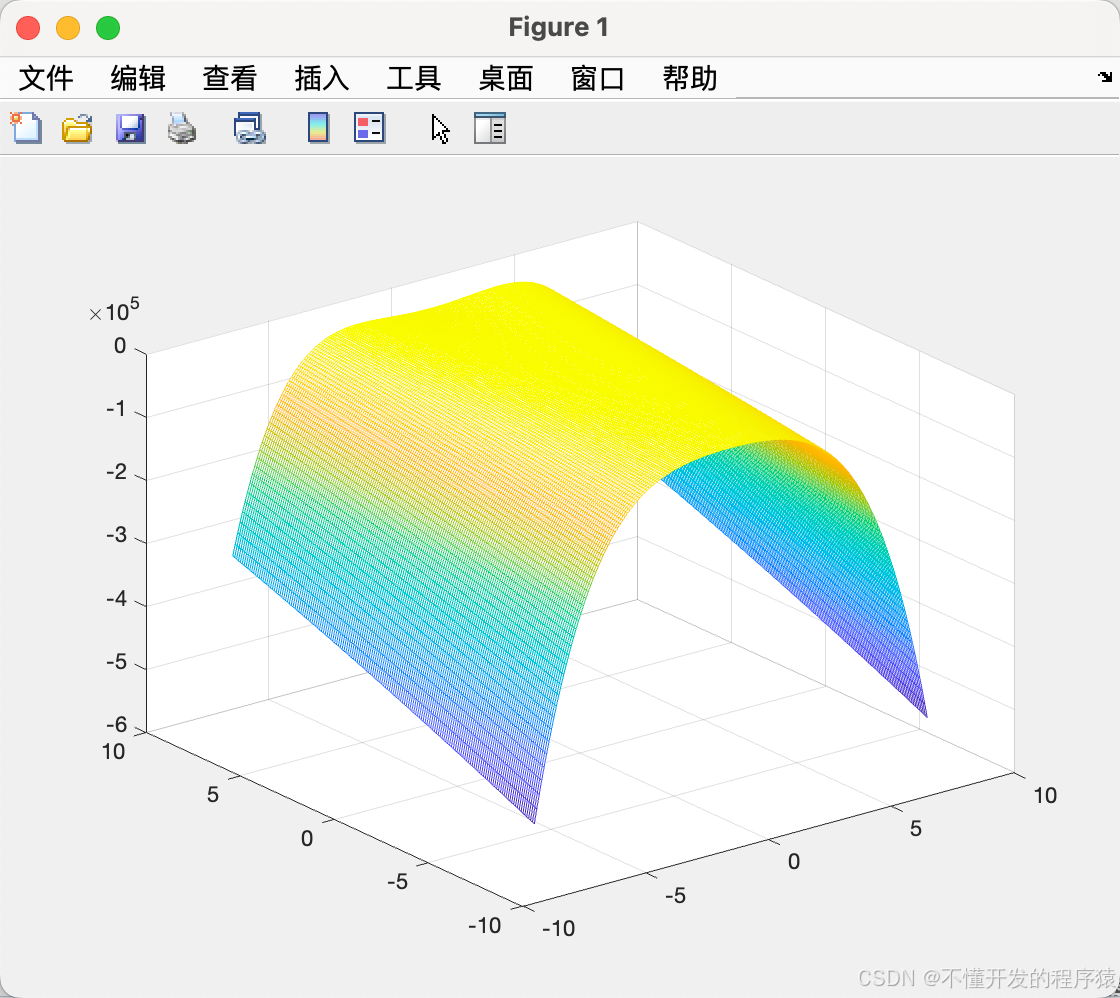
3. 无约束函数极值寻优
3.1 待求解极值函数图形
% 经典函数
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
x1=-0.5:0.01:0.5;
x2=-0.5:0.01:0.5;
for i=1:101
for j=1:101
% object function
z(i,j)=-20*exp(-0.2*sqrt((x1(i)^2+x2(j)^2)/2))-exp((cos(2*pi*x1(i))+cos(2*pi*x2(j)))/2)+20+2.71289;
end
end
[x,y]=meshgrid(x1,x2);%网格化
mesh(x,y,z) %画图
% surf(x,y,z)
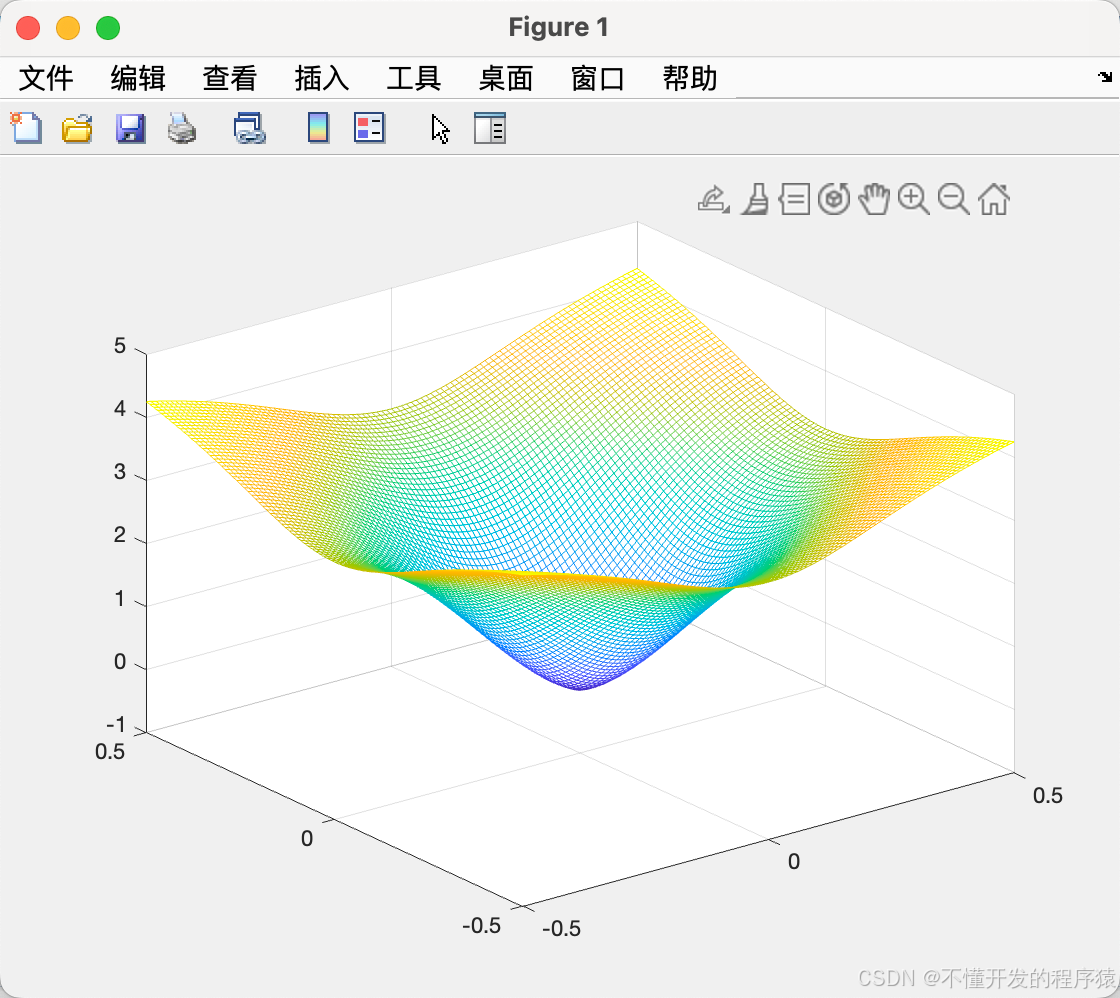
%% 清空环境
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;
maxg=200; % 进化次数
sizepop=20; %种群规模
Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;
%% 产生初始粒子和速度
for i=1:sizepop
%随机产生一个种群
pop(i,:)=5*rands(1,2); %初始种群
V(i,:)=rands(1,2); %初始化速度
%计算适应度
fitness(i)=fun(pop(i,:)); %适应度
end
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:); %全局最佳
gbest=pop; %个体最佳
fitnessgbest=fitness; %个体最佳适应度值
fitnesszbest=bestfitness; %全局最佳适应度值
%% 迭代寻优
for i=1:maxg
maxg %迭代次数
for j=1:sizepop
%速度更新
V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
V(j,find(V(j,:)>Vmax))=Vmax;
V(j,find(V(j,:)<Vmin))=Vmin;
%种群更新
pop(j,:)=pop(j,:)+0.5*V(j,:);
pop(j,find(pop(j,:)>popmax))=popmax;
pop(j,find(pop(j,:)<popmin))=popmin;
%自适应变异
if rand>0.8
k=ceil(2*rand);
pop(j,k)=rand;
end
%适应度值
fitness(j)=fun(pop(j,:));
%个体最优更新
if fitness(j) < fitnessgbest(j)
gbest(j,:) = pop(j,:);
fitnessgbest(j) = fitness(j);
end
%群体最优更新
if fitness(j) < fitnesszbest
zbest = pop(j,:);
fitnesszbest = fitness(j);
end
end
yy(i)=fitnesszbest;
end
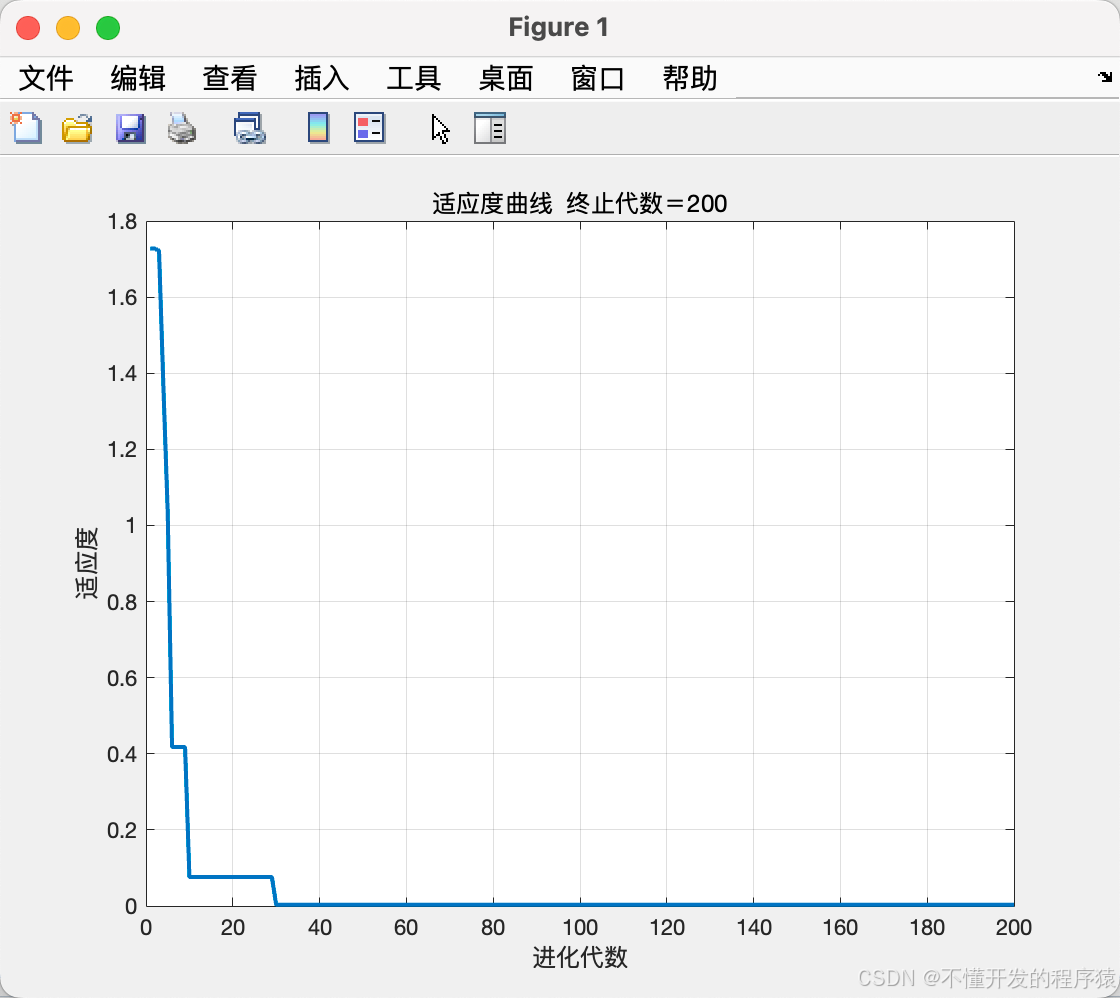
%% 结果分析
plot(yy,'Linewidth',2)
title(['适应度曲线 ' '终止代数=' num2str(maxg)]);
grid on
xlabel('进化代数');ylabel('适应度');
% 结果输出
zbest %最佳个体值
3.2 有约束函数极值APSO寻优
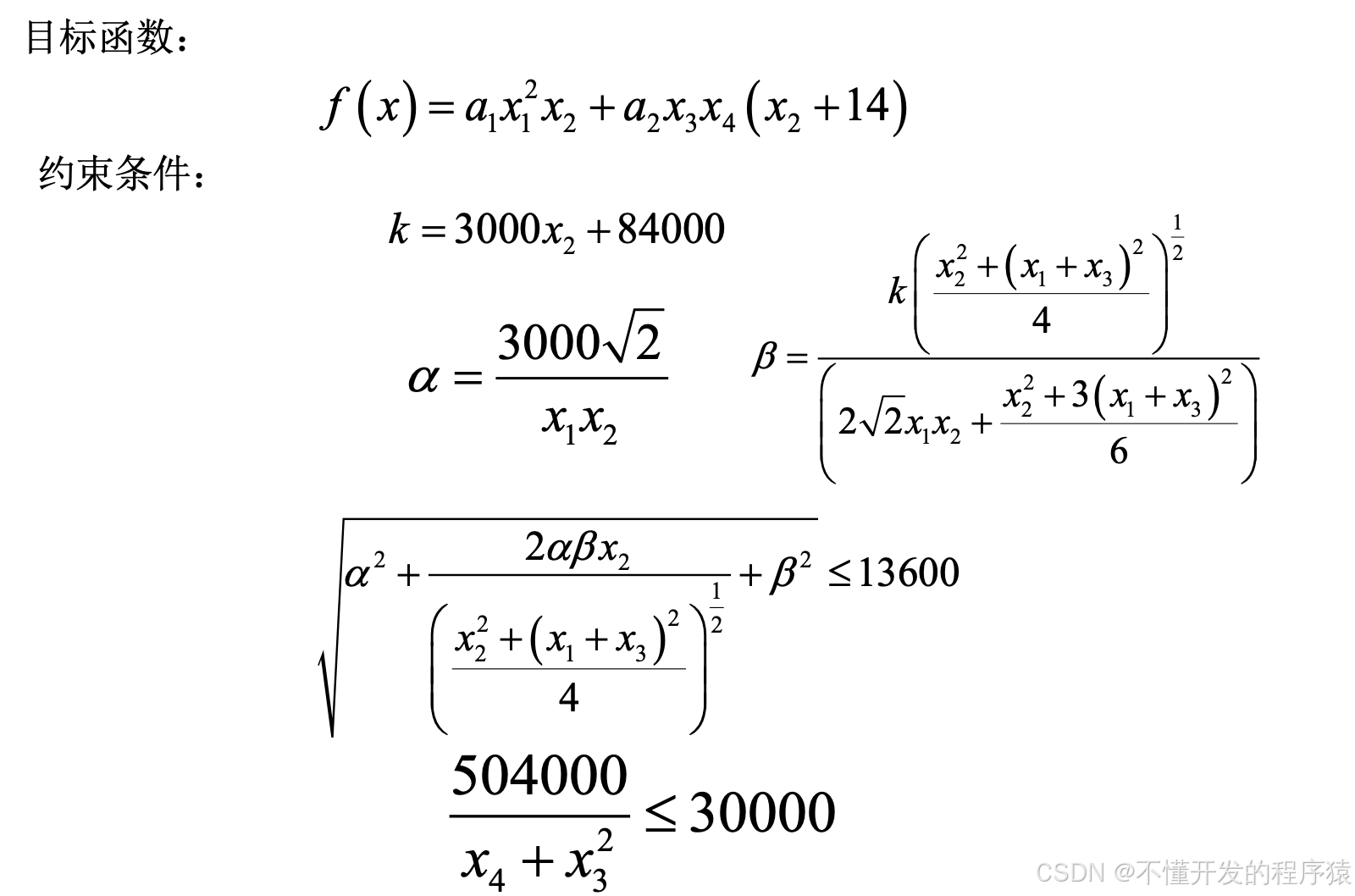
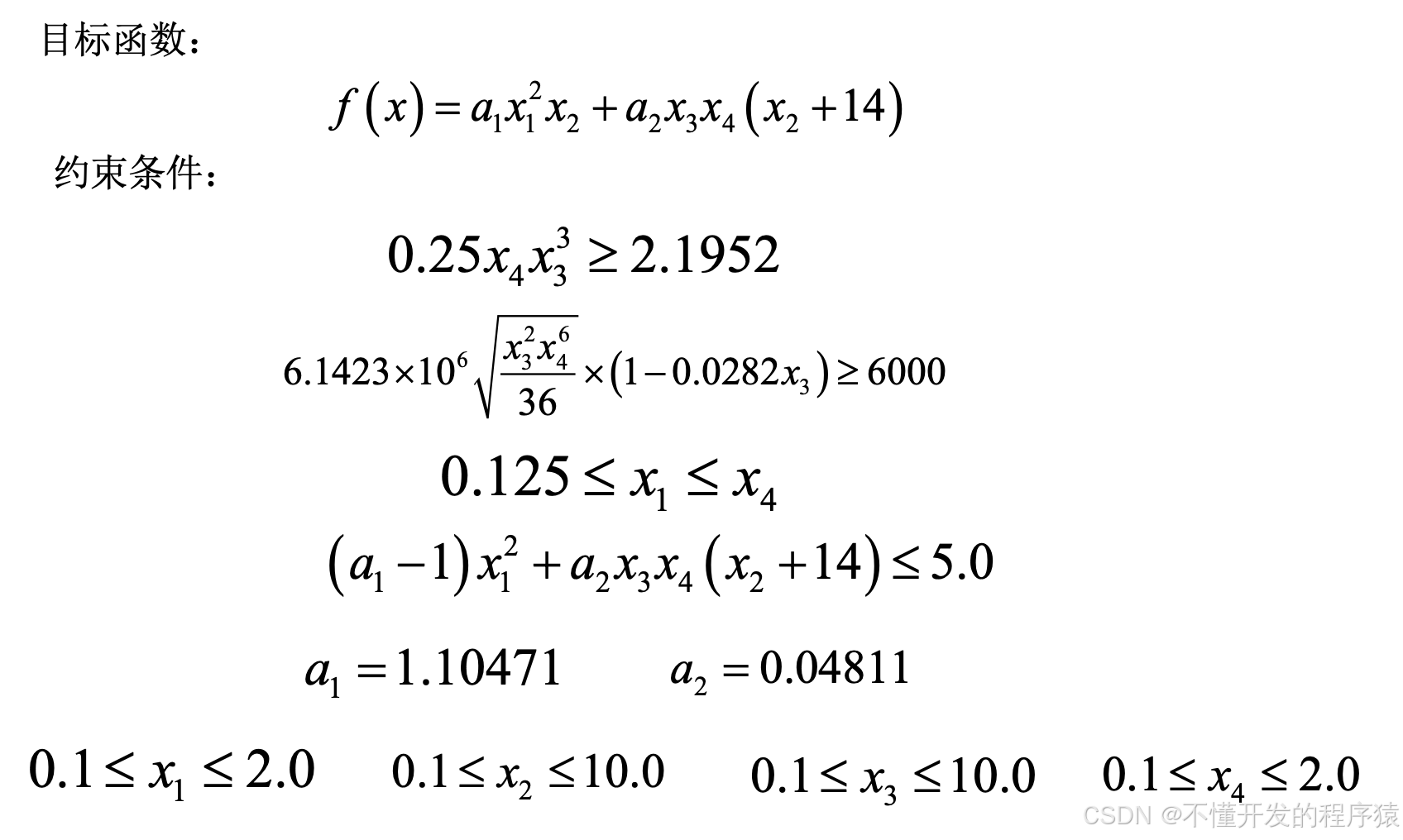
% 改进的快速粒子群优化算法 (APSO):
function apso
Lb=[0.1 0.1 0.1 0.1]; %下边界
Ub=[2.0 10.0 10.0 2.0]; %上边界
% 默认参数
para=[25 150 0.95]; %[粒子数,迭代次数,gama参数]
% APSO 优化求解函数
[gbest,fmin]=pso_mincon(@cost,@constraint,Lb,Ub,para);
% 输出结果
Bestsolution=gbest % 全局最优个体
fmin
%% 目标函数
function f=cost(x)
f=1.10471*x(1)^2*x(2)+0.04811*x(3)*x(4)*(14.0+x(2));
% 非线性约束
function [g,geq]=constraint(x)
% 不等式限制条件
Q=6000*(14+x(2)/2);
D=sqrt(x(2)^2/4+(x(1)+x(3))^2/4);
J=2*(x(1)*x(2)*sqrt(2)*(x(2)^2/12+(x(1)+x(3))^2/4));
alpha=6000/(sqrt(2)*x(1)*x(2));
beta=Q*D/J;
tau=sqrt(alpha^2+2*alpha*beta*x(2)/(2*D)+beta^2);
sigma=504000/(x(4)*x(3)^2);
delta=65856000/(30*10^6*x(4)*x(3)^3);
F=4.013*(30*10^6)/196*sqrt(x(3)^2*x(4)^6/36)*(1-x(3)*sqrt(30/48)/28);
g(1)=tau-13600;
g(2)=sigma-30000;
g(3)=x(1)-x(4);
g(4)=0.10471*x(1)^2+0.04811*x(3)*x(4)*(14+x(2))-5.0;
g(5)=0.125-x(1);
g(6)=delta-0.25;
g(7)=6000-F;
% 如果没有等式约束,则置geq=[];
geq=[];
%% APSO Solver
function [gbest,fbest]=pso_mincon(fhandle,fnonlin,Lb,Ub,para)
if nargin<=4,
para=[20 150 0.95];
end
n=para(1);% 粒子种群大小
time=para(2); %时间步长,迭代次数
gamma=para(3); %gama参数
scale=abs(Ub-Lb); %取值区间
% 验证约束条件是否合乎条件
if abs(length(Lb)-length(Ub))>0,
disp('Constraints must have equal size');
return
end
alpha=0.2; % alpha=[0,1]粒子随机衰减因子
beta=0.5; % 收敛速度(0->1)=(slow->fast);
% 初始化粒子群
best=init_pso(n,Lb,Ub);
fbest=1.0e+100;
% 迭代开始
for t=1:time,
%寻找全局最优个体
for i=1:n,
fval=Fun(fhandle,fnonlin,best(i,:));
% 更新最有个体
if fval<=fbest,
gbest=best(i,:);
fbest=fval;
end
end
% 随机性衰减因子
alpha=newPara(alpha,gamma);
% 更新粒子位置
best=pso_move(best,gbest,alpha,beta,Lb,Ub);
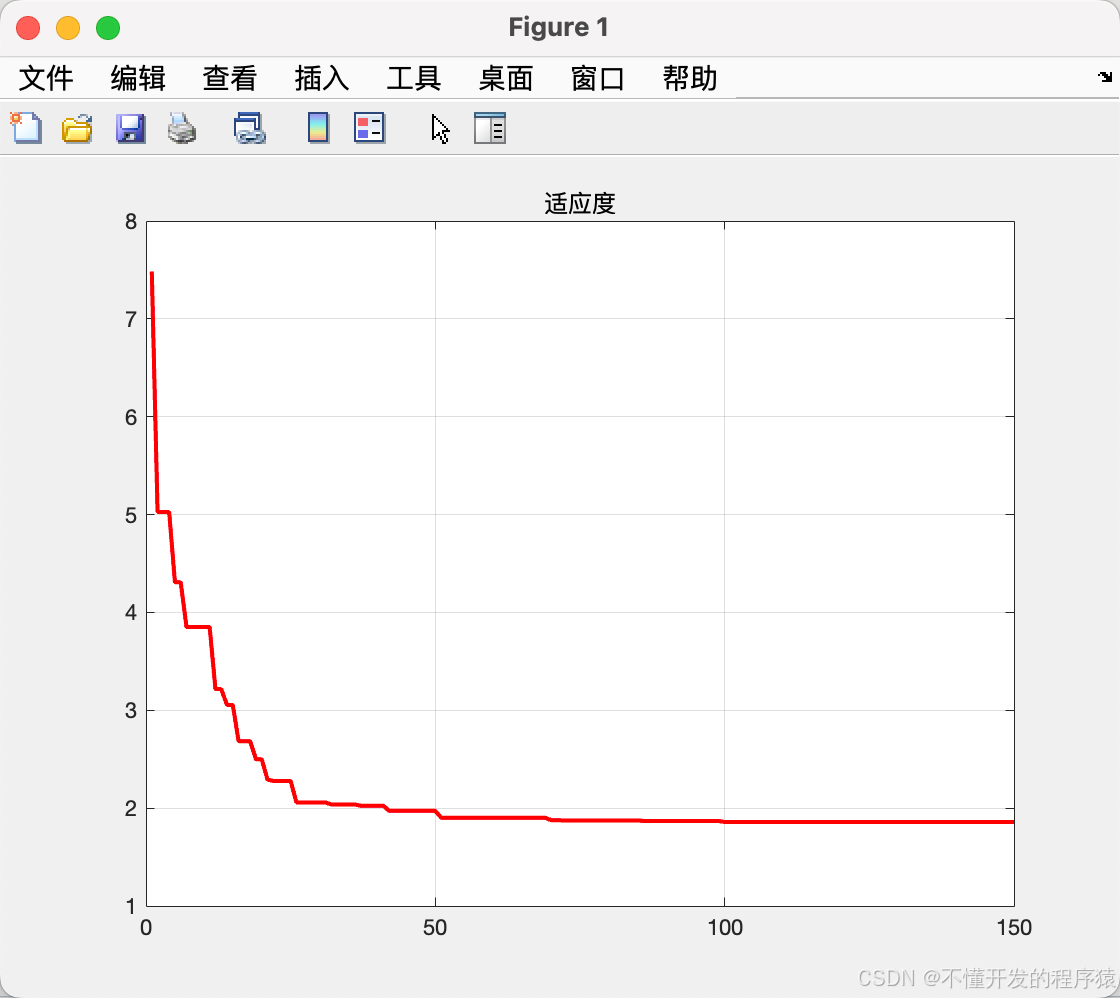
% 结果显示
str=strcat('Best estimates: gbest=',num2str(gbest));
str=strcat(str,' iteration='); str=strcat(str,num2str(t));
disp(str);
fitness1(t)=fbest;
plot(fitness1,'r','Linewidth',2)
grid on
hold on
title('适应度')
end
% 初始化粒子函数
function [guess]=init_pso(n,Lb,Ub)
ndim=length(Lb);
for i=1:n,
guess(i,1:ndim)=Lb+rand(1,ndim).*(Ub-Lb);
end
%更新所有的粒子 toward (xo,yo)
function ns=pso_move(best,gbest,alpha,beta,Lb,Ub)
% 增加粒子在上下边界区间内的随机性
n=size(best,1); ndim=size(best,2);
scale=(Ub-Lb);
for i=1:n,
ns(i,:)=best(i,:)+beta*(gbest-best(i,:))+alpha.*randn(1,ndim).*scale;
end
ns=findrange(ns,Lb,Ub);
% 边界函数
function ns=findrange(ns,Lb,Ub)
n=length(ns);
for i=1:n,
% 下边界约束
ns_tmp=ns(i,:);
I=ns_tmp<Lb;
ns_tmp(I)=Lb(I);
% 上边界约束
J=ns_tmp>Ub;
ns_tmp(J)=Ub(J);
%更新粒子
ns(i,:)=ns_tmp;
end
% 随机性衰减因子
function alpha=newPara(alpha,gamma);
alpha=alpha*gamma;
% 带约束的d维目标函数的求解
function z=Fun(fhandle,fnonlin,u)
% 目标
z=fhandle(u);
z=z+getconstraints(fnonlin,u); % 非线性约束
function Z=getconstraints(fnonlin,u)
% 罚常数 >> 1
PEN=10^15;
lam=PEN; lameq=PEN;
Z=0;
% 非线性约束
[g,geq]=fnonlin(u);
%通过不等式约束建立罚函数
for k=1:length(g),
Z=Z+ lam*g(k)^2*getH(g(k));
end
% 等式条件约束
for k=1:length(geq),
Z=Z+lameq*geq(k)^2*geteqH(geq(k));
end
% Test if inequalities
function H=getH(g)
if g<=0,
H=0;
else
H=1;
end
% Test if equalities hold
function H=geteqH(g)
if g==0,
H=0;
else
H=1;
end
–end–

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容








所有评论(0)