raw数据噪声模型和标定

噪声在ISP中去得越早越好，因为噪声在最开始成像的过程中就引入了，之后只会不断放大。具体而言，噪声产生的位置就是上图中绿色框的区域。

zcg1942

4233人浏览 · 2024-03-01 15:00:38

zcg1942 · 2024-03-01 15:00:38 发布

上图是一个简单的ISP流程图。噪声产生的位置就是上图中绿色框的区域。噪声在ISP中去得越早越好，因为噪声在最开始成像的过程中就引入了，之后只会不断放大。

下图可以更加清楚地看到噪声是在何处产生，何处被放大。图片来源https://www.ecva.net/papers/eccv_2020/papers_ECCV/papers/123510001.pdf

第一步是光电效应，光子以一个量子效率转换为电子。除了光子转换带来电子，受温度影响电路本身也会产生热/暗噪声。然后经过模拟增益，还有读出和量化噪声。

商汤文章：Rethinking Noise Synthesis and Modeling in Raw Denoising用公式噪声，和上图应该是匹配的：

$K_a,K_q$ 分别表示模拟和数字增益。 $N_p,N_q$ 分别表示与信号相关的shot noise和量化过程的噪声。 $N_1,N_2$ 分别表示两次增益之前的其他噪声。

不管什么噪声，他们的分布一般都可以使用泊松分布或者高斯分布描述。

1.泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。

泊松分布从二项分布中推导出来。因为二项分布只有0，1两种取值，所以需要将所关心的时间段切片，在子窗内看作是二项分布。化整为零到极限就是：

利用二项分布的期望公式，可以求得p的表达：

$E(x)=np=\mu, p=\frac{\mu}{n}$

最后代入，化简，得到该段时间内k个取1的概率：

在泊松分布中，把 $\mu$ 称为事件比率 (event rate)，使用 $\lambda$ 表示。只需要知道”比率“，不用知道划分次数n和概率p。

1. 在工程应用中，当n＞20，并且p≤0.05（发生概率5%，稀有事件）时，就可以用泊松分布近似表示二项分布。

2.泊松分布的均值和方差都是 $\lambda$ ，均值越大方差越大，分布也就越分散，越接近高斯分布。

3. 每个时间单元的事件平均发生比率是常数时，才可以使用泊松分布。这意味着时间单元不能太短

4. 不同时间单元应该互相独立，互不影响

1.1散粒噪声

在拍摄的时候光线进入sensor，光的波粒二象性，就可以看作是离散的粒子散落在sensor上，所以每个像素得到的光线是不同的，就有泊松噪声。

泊松分布的关键参数就是lambda。

泊松分布本质是n重伯努利分布，从推导可以看出， $k!$ 来自于排列组合A->C的计算公式， $\lambda ^k$ 来自于 $p^k=(\frac{\lambda}{n})^k$ ，先表示二项分布p，然后发生k次以指数的形式表示。

泊松分布的特点就是均值和方差相等，

所以曝光时间越长，lambda就越大，方差就越大，图像噪声越大。

根据极限定理，当lambda极大时，可以使用相同均值方差的高斯分布近似泊松分布。当暗环境时，近似是不成立的。

1.2热/暗噪声

除了光电效应会释放电子，温度升高也会释放更多的电子。暗噪声也服从泊松分布。

温度每增加6度，噪声水平升高一倍。暗噪声和曝光时间正线性相关。

天文望远镜中，为了避免暗噪声，会降低温度，减少曝光时间，或者提前标定，到时候减去暗噪声。

1.3 合并

散粒噪声和暗噪声都是泊松分布，且在ISP中处于相同的位置，所以二者可以合并为一个新的泊松噪声L：参数是 $t \cdot (a\cdot \Phi +D)$ ，

因为散粒噪声和暗噪声都和时间相关，所以把时间t可以提出来，D表示温度相关， $\alpha$ 和 $\Phi$ 的乘积表示光子平均数。

2.高斯分布

高斯分布，又称“正态分布（normal distribution）”，是概率统计中最常见的连续概率分布之一。它以著名数学家卡尔·弗里德里希·高斯的名字命名。

高斯分布在自然界和社会现象中无处不在，它反映了数据分布的一般规律。它的基本原理可以归纳为最小二乘法和中心极限定理。

2.1读出噪声（Readout Noise，RN）

光电子要经过模拟放大器、ADC之后才会形成数字信号：

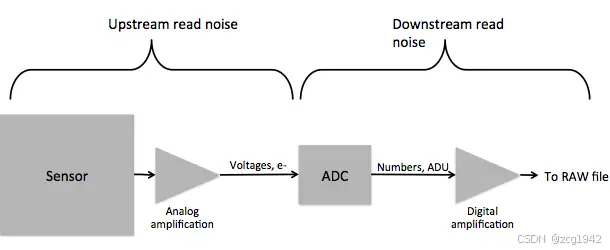
读出噪声又分为增益之前（ISO生效之前）的upstream read noise和之后的downstream read noise。

upstream read noise和信号随着ISO同步放大，只和ISO有关，而与信号无关。ISO固定，任凭曝光量如何变，读出噪声不变。而downstream read noise可以认为是一个固定值。

2.2 ADC噪声

ADC，Analog-to-Digital Converter的缩写,指模/数转换器或者模数转换器 。ADC不是理想的（存在电磁干扰、本身具有热效应等），转换的过程会产生一定的误差，这就是ADC噪声，ADC噪声也包括量化噪声：

上述图像源于1948年贝尔实验室的W. R. Bennett发表的经典论文。

3.仿射噪声模型

1.3中合并的泊松噪声会经过gain放大。此部分为和信号相关的噪声。

高斯噪声和信号无关，但是部分读出噪声会被放大，ADC噪声不会。

所以仿射噪声模型整体分为：信号相关的噪声*g+信号无关的噪声。

$I=L\cdot g+n_{read}\cdot g+n_{ADC}=L\cdot g+n_{add}$

对应图示：

因为泊松噪声均值和方差的特点，可以看到图像方差是图像均值关于g的线性函数：

$\sigma(I)^2 =E(I)\cdot g+\sigma _{add}^2$

4. 信噪比

光子噪声和信号强度有关。高斯噪声和信号无关。所以信号越强，光子噪声占主导，信号弱时高斯噪声占主导。

场景亮时

亮度高的时候，高斯忽略不计。这时不管是模拟增益还是数字增益，分子分母部分的增益都会抵消。只要曝光量增加，SNR就会增加。

场景暗时

场景暗时讨论两种选择，后期再数字放大，和增加ISO模拟增益。

为了把照片提亮到某一亮度，可以理解为把信号放大A倍，如果使用ISO（这里特指模拟增益）放大，那么downstream read noise不会被放大；如果使用最后的数字增益，同时还会放大downstream read noise，这在downstream read noise较大时更加不可接受，比如佳能相机。

所以，只要不过曝，ISO越高效果越好：

那为什么有很多人说ISO大会带来噪点呢？

亮度低的时候，光子噪声忽略不计。如果图像亮度保持不变（即SNR的分子不变时），ISO越大，增益g越大，SNR越低。

5. 标定

5.1信号相关噪声标定

方法是线性拟合。当暗噪声被减去后，图像方差仍然是图像均值的线性函数。

$\sigma(I)^2 =E(I)\cdot g+\sigma _{add}^2$

可以看到方差和图像亮度和增益g都成线性关系。在同一个曝光组合下拍摄不同灰度色卡（可以使用ISO12233解析度分辨率卡），计数不同灰度下的方差，使用Stats.linregress( )对色卡均值和方差做线性回归，横坐标为灰度，纵坐标为方差，可以得到斜率和截距。斜率是增益g，截距是高斯加性噪声。

关于斜率。因为泊松噪声的特殊性，经过增益后方差被放大 $g^2$ 倍，均值被放大 $g$ 倍，所以可以直接得到方差为E(I)*g。可以得到不同ISO下的斜率，很明显增益g和ISO（ISO指的是a gain*d gain）成正相关，可以考虑使用直线拟合斜率和ISO的关系。

关于截距。注意这里的截距指高斯加性噪声，包含了读出噪声和ADC噪声：

$\sigma_{add} =\sigma_{read}\cdot g+\sigma_{ADC}$

5.2 信号无关噪声标定

正如刚才估计截距时所说的，加性噪声分为两部分：

加性噪声是和信号无关的，但是有一部分（读出噪声）是和增益有关的。乘一个系数，对应方差变为系数的平方倍，而增益系数与ISO是线性的，所以方差和ISO的关系可以使用二次函数表示，曲线形式为开口向上的二次曲线。使用np.polyfit最小二乘法进行多项式拟合，会标定得到三个数，分别是二次项系数，一次项系数，常数项。

通常使用黑帧的方法也可以得到加性噪声，使得信号为0，得到的数据自然就是信号无关的噪声。

reference：

图像算法原理与实践——图像复原之噪声模型 - 知乎

https://zhuanlan.zhihu.com/p/397873289

http://graphics.cs.cmu.edu/courses/15-463/2020_fall/lectures/lecture7.pdf