计算机图形学实验——二次Bezier曲线 & 双三次Bezier曲面绘制 (dialog-based MFC project) (附源码)

使用VS2022基于对话框的MFC项目模板，绘制二次贝塞尔曲线和双三次贝塞尔曲面

Yushan_Ji

1756人浏览 · 2023-11-29 22:06:43

Yushan_Ji · 2023-11-29 22:06:43 发布

Bezier曲线曲面绘制

源码：Yushan-Ji/ComputerGraphics: ECNU2023秋计算机图形学课程实验代码 (github.com)
ps.若github.com国内网络无法访问，可使用镜像Yushan-Ji/ComputerGraphics: ECNU2023秋计算机图形学课程实验代码 (githubfast.com)

文章目录

Bezier曲线曲面绘制

实验内容

绘制低次Bezier、B样条或NURBS曲线
绘制双三次Bezier或B样条曲面

实验思路

二次Bezier曲线

二次贝塞尔曲线是由三个控制点定义的曲线，通常表示为 $P_0$ 、 $P_1$ 和 $P_2$ 。曲线的公式如下：

$t)^2 \cdot P_0 + 2 \cdot (1 - t) \cdot t \cdot P_1 + t^2 \cdot P_2 \quad (t\in [0,1])$
其中， $P_0$ 是起始点， $P_1$ 是控制点， $P_2$ 是终点。

我们使用下面的公式计算曲线上的点：

$\begin{cases} x(t) = (1 - t)^2 \cdot x_0 + 2 \cdot (1 - t) \cdot t \cdot x_1 + t^2 \cdot x_2 \\ y(t) = (1 - t)^2 \cdot y_0 + 2 \cdot (1 - t) \cdot t \cdot y_1 + t^2 \cdot y_2 \end{cases}$
其中， $x_0, y_0)$ 是起始点坐标，$(x_1, y_1) $是控制点坐标，$ (x_2, y_2) $是终点坐标；通过给定一系列离散的$ t$值，实现绘制平滑的Bezier曲线（t越小曲线越平滑）。

双三次Bezier曲面

双三次贝塞尔曲面是由16个控制点定义的曲面，通常表示为4x4矩阵。

曲面的公式如下：
$\sum_{i=0}^3 \sum_{j=0}^3 P_{ij} \cdot B_i^3(u) \cdot B_j^3(v) \quad (u,v\in [0,1])$
其中， $P_{ij}$ 是曲面上的控制点； $B_i^3(u)$ 和 $B_j^3(v)$ 是三次贝塞尔基函数，定义如下：

$B_i^3(u) = C_3^i \cdot u^i \cdot (1 - u)^{3-i}\\ B_j^3(v) = C_3^j \cdot v^j \cdot (1 - v)^{3-j}$
计算曲面上的点的公式如下：

$\sum_{i=0}^3 \sum_{j=0}^3 x_{ij} \cdot B_i^3(u) \cdot B_j^3(v)\\ y(u, v) = \sum_{i=0}^3 \sum_{j=0}^3 y_{ij} \cdot B_i^3(u) \cdot B_j^3(v)$
通过给定一系列离散的 $u, v$ 值，实现绘制平滑的Bezier曲面（ $u, v$ 越小，面片就越小，曲面越平滑）。

核心代码

对话框

在resource.h文件中新增下列组件：

#define IDD_BEZIERCURVE_DIALOG          129    // 主对话框
#define IDC_STATIC_CANVAS               1000   // 绘制曲线的绘图框
#define IDC_STATIC_CANVAS_SURFACE       1001   // 绘制曲面的绘图框
#define IDC_BUTTON1                     1002   // 绘制曲面的按钮

对话框设计如下：

头文件

// BezierCurve.h : header file
#pragma once
#include <vector>

// BezierCurve dialog
class BezierCurve : public CDialogEx
{
	// Construction
public:
	BezierCurve(CWnd* pParent = nullptr);	// standard constructor

	// Dialog Data
#ifdef AFX_DESIGN_TIME
	enum { IDD = IDD_BEZIER_DIALOG };
#endif

protected:
	virtual void DoDataExchange(CDataExchange* pDX);	// DDX/DDV support


	// Implementation
protected:
	HICON m_hIcon;

	// Generated message map functions
	virtual BOOL OnInitDialog();
	afx_msg void OnSysCommand(UINT nID, LPARAM lParam);
	afx_msg void OnPaint();
	afx_msg void OnLButtonDown(UINT nFlags, CPoint point); // 左键点击
	afx_msg void OnRButtonDown(UINT nFlags, CPoint point); // 右键点击
	DECLARE_MESSAGE_MAP()

public:
  // Bezier曲线
	std::vector<CPoint> points;
	bool IsCompleted;
  CPoint BezierCurvePoint(CPoint p0, CPoint p1, CPoint p2, double t);
	void DrawBezierCurve();
  
  // Bezier曲面
	CPoint controlPoints[4][4];    // 16个控制点
	CPoint surfacePoints[50][50];  // 2500个曲面点
	void GenerateControlPoints();  // 随机生成控制点
	int Combination(int n, int k); // 计算组合数
	CPoint BezierSurfacePoint(float u, float v); // 计算每一个曲面上的点
	void DrawBezierSurface(); //绘制曲面
};

头文件中类BezierCurve的构造函数如下：

BezierCurve::BezierCurve(CWnd* pParent /*=nullptr*/)
	: CDialogEx(IDD_BEZIERCURVE_DIALOG, pParent)
{
	m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);
	IsCompleted = false;
	points.clear();
}

消息函数

BEGIN_MESSAGE_MAP(BezierCurve, CDialogEx)
	ON_WM_SYSCOMMAND()
	ON_WM_PAINT()
	ON_WM_LBUTTONDOWN()
	ON_WM_RBUTTONDOWN()
	ON_BN_CLICKED(IDC_BUTTON1, &BezierCurve::DrawBezierSurface)
END_MESSAGE_MAP()

曲线绘制相关函数实现

// 在OnPaint()中调用绘制曲线的函数
void BezierCurve::OnPaint()
{
	DrawBezierCurve();
}

// 鼠标左键单击绘制起点、控制点和终点
void BezierCurve::OnLButtonDown(UINT nFlags, CPoint point)
{
	if (IsCompleted)
		return;
	else
	{
		points.push_back(point);

		// 若不是第一个点，则连接当前点和上一个点
		if (points.size() > 1)
		{
			CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS);
			CDC* pDC = CANVAS->GetDC();
			pDC->MoveTo(points[points.size() - 2]);
			pDC->LineTo(point);
			ReleaseDC(pDC);
		}
	}
}

// 右键单击表示绘制完毕，将IsCompleted设置为true，阻止后续对左键单击的响应
void BezierCurve::OnRButtonDown(UINT nFlags, CPoint point)
{
	IsCompleted = true;
	return;
}

// 计算每一个曲线上的点
CPoint BezierCurve::BezierCurvePoint(CPoint p0, CPoint p1, CPoint p2, double t)
{
	double x = 0.0;
	double y = 0.0;
	x = (1 + t * t - 2 * t) * p0.x + 2 * (t - t * t) * p1.x + t * t * p2.x;
	y = (1 + t * t - 2 * t) * p0.y + 2 * (t - t * t) * p1.y + t * t * p2.y;
	CPoint point((int)x, (int)y);
	return point;
}

// 绘制曲线
void BezierCurve::DrawBezierCurve()
{
	if (IsCompleted && points.size() >= 3)
	{
		double t = 0.0;
    // 获取绘图区
		CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS);
		CDC* pDC = CANVAS->GetDC();

		CPoint tempPoint = BezierCurvePoint(points[0], points[1], points[2], t);
		CPoint oldPoint = tempPoint;

		while (t <= 1)
		{
			tempPoint = BezierCurvePoint(points[0], points[1], points[2], t);
			pDC->MoveTo(oldPoint);
			pDC->LineTo(tempPoint);
			oldPoint = tempPoint;
			t += 0.01;
		}
		ReleaseDC(pDC);
	}
}

曲面绘制相关函数实现

// 随机产生16个控制点
void BezierCurve::GenerateControlPoints()
{
  // 获取绘图区的大小，以免控制点超出绘图区范围
	CRect Area;
	GetDlgItem(IDC_STATIC_CANVAS_SURFACE)->GetClientRect(Area);
	int width = Area.Width();
	int height = Area.Height();
  // 随机种子
	std::srand(static_cast<unsigned int>(std::time(0)));
	for (int i = 0; i < 4; ++i)
	{
		for (int j = 0; j < 4; ++j)
		{
			int x = std::rand() % (width + 1);
			int y = std::rand() % (height + 1);
			controlPoints[i][j] = CPoint(x, y);
		}
	}
}

// 实现组合数计算的函数
int BezierCurve::Combination(int n, int k)
{
	if (k == 0 || k == n)
		return 1;
	else
		return Combination(n - 1, k - 1) + Combination(n - 1, k);
}

CPoint BezierCurve::BezierSurfacePoint(float u, float v)
{
	float x = 0.0;
	float y = 0.0;
	// 计算双三次贝塞尔曲面上的点坐标
	for (int i = 0; i < 4; ++i)
	{
		for (int j = 0; j < 4; ++j)
		{
			float coef = float(Combination(3, i) * Combination(3, j) * pow(u, i) * pow(1 - u, 3 - i) * pow(v, j) * pow(1 - v, 3 - j));
			x += controlPoints[i][j].x * coef;
			y += controlPoints[i][j].y * coef;
		}
	}
	return CPoint(x, y);
}

void BezierCurve::DrawBezierSurface()
{
  // 获取绘图区
	CStatic* CANVAS = (CStatic*)GetDlgItem(IDC_STATIC_CANVAS_SURFACE);
	CDC* pDC = CANVAS->GetDC();
  
	// 产生随机控制点
	GenerateControlPoints();
  
	// 计算曲面上的所有点并存储，便于后续绘制面片
	int i = 0, j = 0;
	for (int i = 0; i < 50; i++)
	{
		for (int j = 0; j < 50; j++)
		{
			float u = i / 50.0;  // 将i映射到范围[0, 1]
			float v = j / 50.0;  // 将j映射到范围[0, 1]
			surfacePoints[i][j] = BezierSurfacePoint(u, v);
		}
	}
  // 绘制面片
	for (i = 1; i < 50; i++)
	{
		for (j = 1; j < 50; j++)
		{
			pDC->MoveTo(surfacePoints[i - 1][j - 1]);
			pDC->LineTo(surfacePoints[i - 1][j]);
			pDC->LineTo(surfacePoints[i][j]);
			pDC->LineTo(surfacePoints[i][j - 1]);
		}
	}
	ReleaseDC(pDC);
}

实验结果

二次Bezier曲线

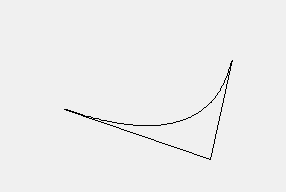
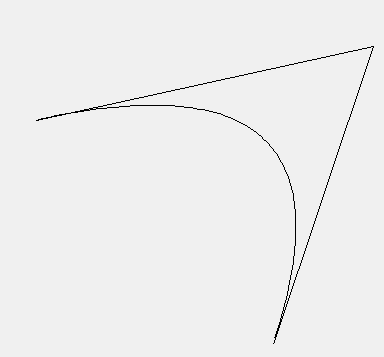
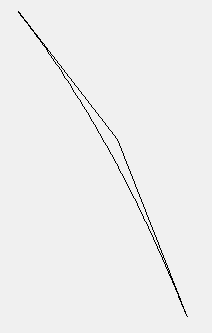
双三次Bezier曲面

实验心得

在绘制Bezier曲面时，我发现函数DrawBezierSurface()中计算曲面点的部分需要将i,j映射到u,v，如下：

int i = 0, j = 0;
for (int i = 0; i < 50; i++)
{
	for (int j = 0; j < 50; j++)
	{
		float u = i / 50.0;  // 将i映射到范围[0, 1]
		float v = j / 50.0;  // 将j映射到范围[0, 1]
		surfacePoints[i][j] = BezierSurfacePoint(u, v);
	}
}

如果将u,v映射到i,j（如下），就会出现每一个surfacePoints[12][j]都为(0,0)的现象，我不太明白为什么？

而且我发现，即使我修改精度，例如u += 0.01，仍然会有每一个surfacePoints[12][j]都为(0,0)的现象。

int i = 0, j = 0;
for (float u = 0; u <= 1.0; u += 0.02)
{
  for (float v = 0; v <= 1.0; v += 0.02)
  {
    CPoint point = BezierSurfacePoint(u, v);
    i = 50 * u;
    j = 50 * v;
    surfacePoints[i][j] = point;
  }
}