目录

1.2.4 系统的因果性和稳定性

线性卷积的计算

1.2.4 系统的因果性和稳定性

稳定系统

解：(1)讨论因果性

(2)讨论稳定性

1.3 常系数差分方程

差分方程表示法的另一优点是可以直接得到系统的结构

1.4 连续时间信号的抽样

1.4.1 采样

一、理想采样

单位冲激函数

二、频谱的周期延拓

1.4.2 采样的恢复

时域分析

---

1.2.4 系统的因果性和稳定性

线性卷积的计算

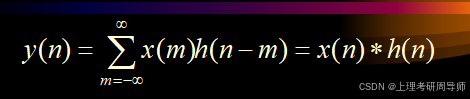
计算它们的卷积的步骤如下：

   (1)折叠：先在哑变量坐标轴k上画出x(k)和h(k)，将h(k)以纵坐标为对称轴折叠成 h(-k)。  

 (2)移位：将h(-k)移位n，得h(n-k)。当n为正数时，右移n；当n为负数时，左移n。  

 (3)相乘：将h(n-k)和x(k)的对应取样值相乘。  

 (4)相加：把所有的乘积累加起来，即得y(n)。

计算线性卷积时，一般要分几个区间分别加以考虑，下面举例说明。

例 已知x(n)和h(n)分别为：

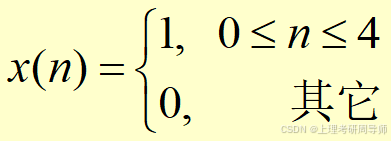
和

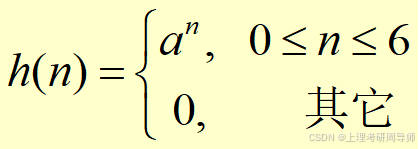
a为常数，且1<a，试求x(n)和h(n)的线性卷积。

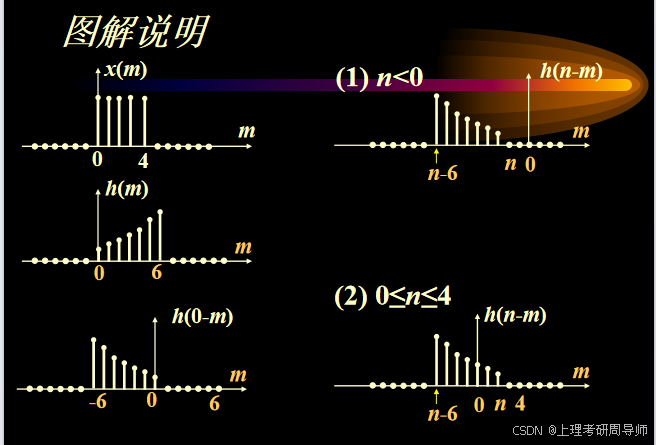
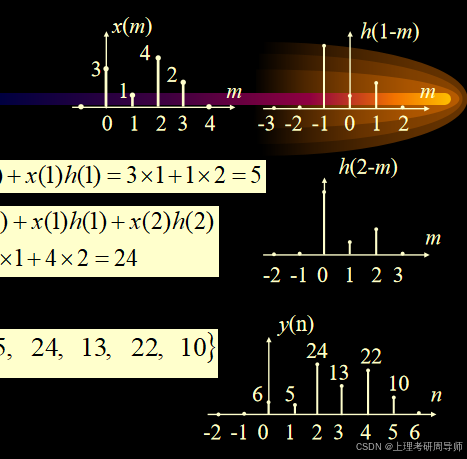
解 参看图，分段考虑如下：

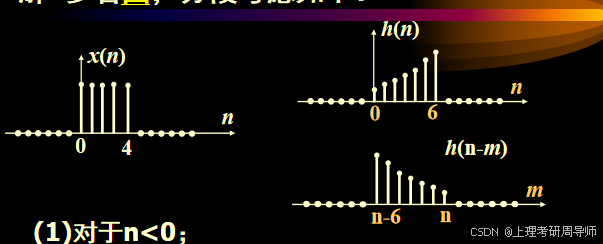
(1)对于n<0；

(2)对于0≤n≤4；

(3)对于n>4，且n-6≤0，即4<n≤6；

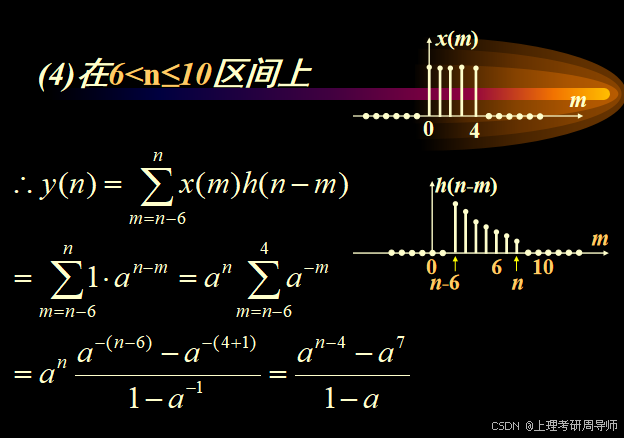
(4)对于n>6，且n-6≤4，即6<n≤10；

(5)对于(n-6)>4，即n>10。

图解说明

(2)在0≤n≤4区间上

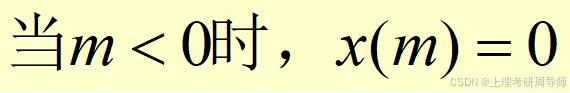
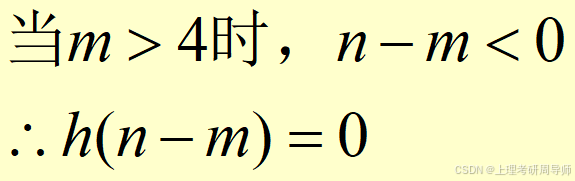
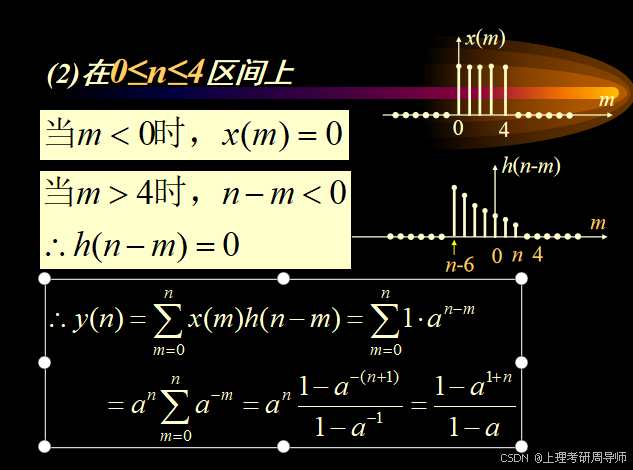
综合以上结果，y(n)可归纳如下：

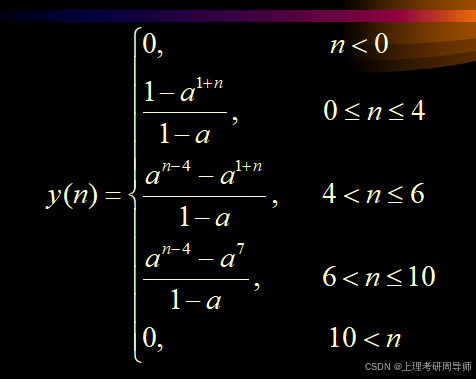
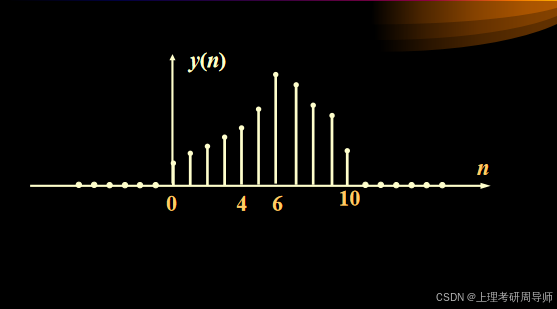
卷积结果y(n)如图所示

设有一线性时不变系统，其单位取样响应为

(2)在0<n<N 区间上

(3)在n>N 区间上

例

设有一线性时不变系统，其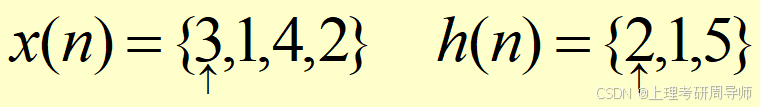

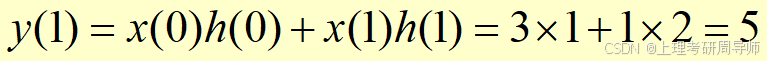
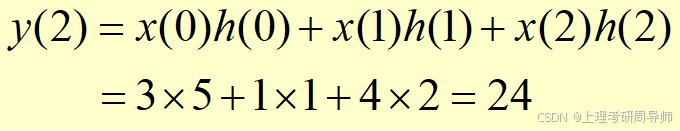
对有限长序列相卷，可用竖乘法

注：

1. 各点要分别乘、分别加且不跨点进位；  

  2. 卷和结果的起始序号等于两序列的其实序号之和。

由上面几个例子的讨论可见，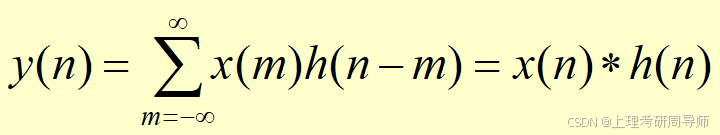

  设x(n)和h(n)两序列的长度分别是N 和M ，线性卷积后的序列长度为(N + M -1)。

线性卷积满足以下运算规律：

交换律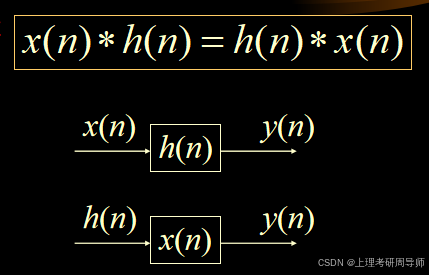

结合律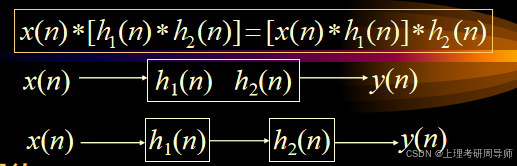

分配律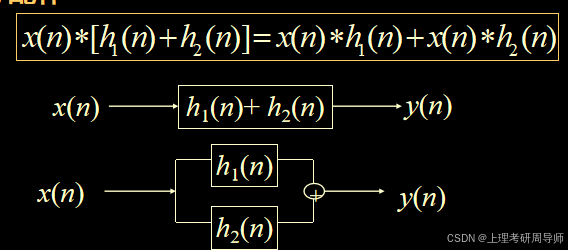

序列本身与单位取样序列的线性卷积等于序列本身：

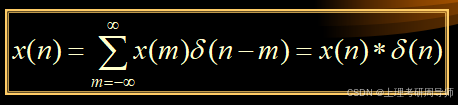
如果序列与一个移位的单位取样序列(n-n0)进行线性卷积，就相当于将序列本身移位n0：

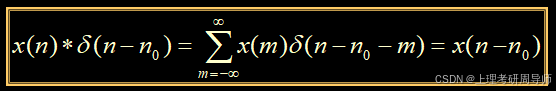
1.2.4 系统的因果性和稳定性

   在系统中，若输出y(n)只取决于n时刻，以及n时刻以前的输入，即

称该系统是因果系统。因果系统是指输出的变化不领先于输入的变化的系统。

对于线性时不变系统，具有因果性的充要条件是系统的单位取样响应满足：

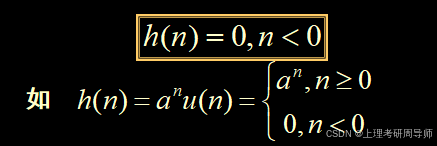
稳定系统

      稳定系统是指对于每个有界输入x(n)，都产生有界输出y(n)的系统。即如果|x(n)|≤M(M为正常数)，有|y(n)|<+∞，则该系统被称为稳定系统。

     对一个线性时不变系统来说，系统稳定的充要条件是单位取样响应绝对可和，即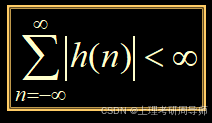

设某线性时不变系统，其单位取样响应为

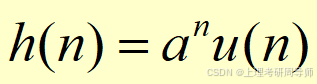
式中a是实常数，试分析该系统的因果稳定性。

解：由于n<0时，h(n)=0，故此系统是因果系统。

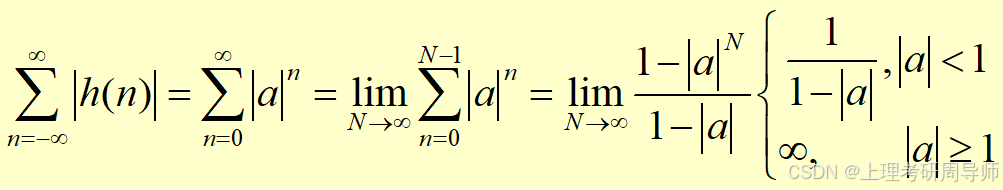
所以 |a|<1  时，此系统是稳定系统。

设某线性时不变系统，其单位取样响应为

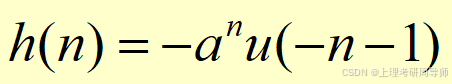
式中a是实常数，试分析该系统的因果稳定性。

解：(1)讨论因果性

由于n<0时，h(n)0，故此系统是非因果系统。

(2)讨论稳定性

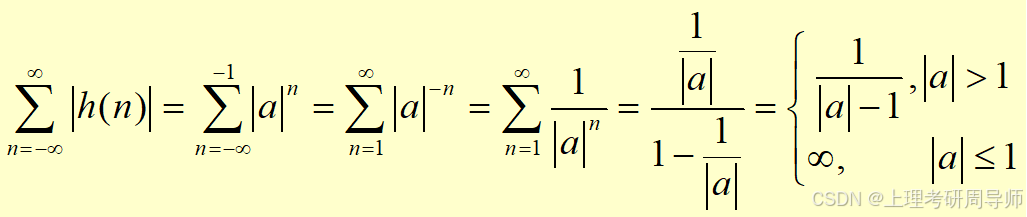
所以 |a|>1 时，此系统是稳定系统。

1.3 常系数差分方程

连续时间线性时不变系统——》线性常系数微分方程

离散时间线性时不变系统——》线性常系数差分方程

一个N 阶线性常系数差分方程用下式表示：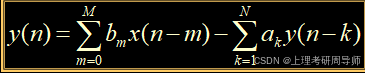

求解差分方程的基本方法有三种：

设差分方程为

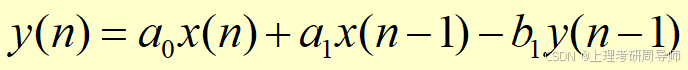
求输出序列设系统参数

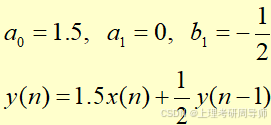
设输入为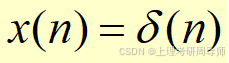

初始条件为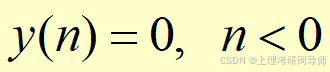

解：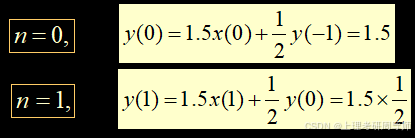

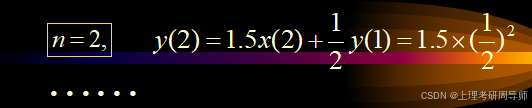
依次类推

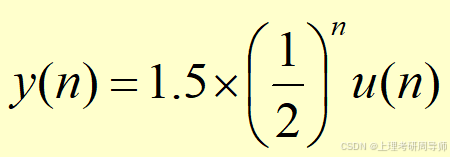
初始条件为

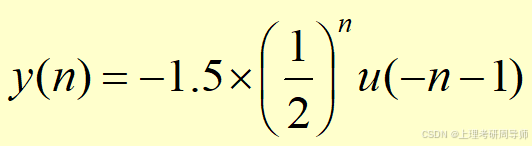
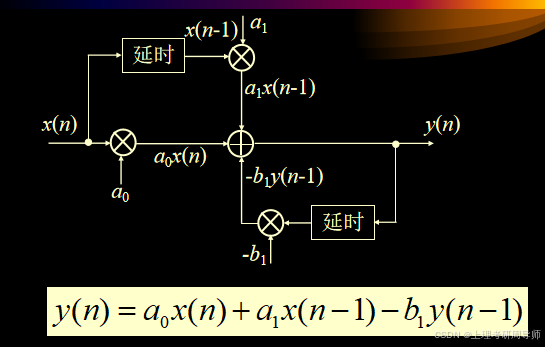
差分方程表示法的另一优点是可以直接得到系统的结构

1.4 连续时间信号的抽样

1.信号经过采样以后，将发生一些什么变化？例如，信号频谱将发生怎样变化；

2.经过采样后信号内容会不会有丢失；

3.如果信号没有被丢失，其反变换应该怎样进行，即由数字信号恢复成模拟信号应该具备那些条件等

1.4.1 采样

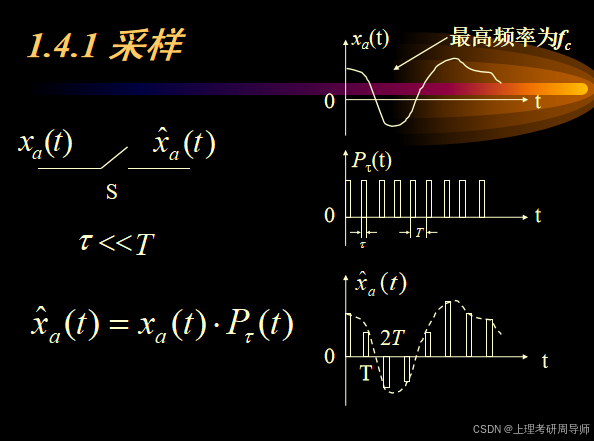
一、理想采样

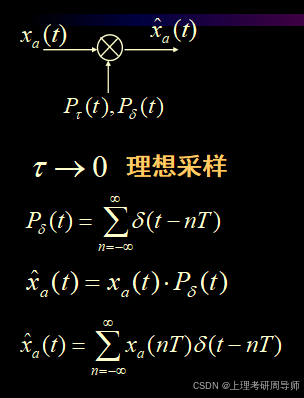
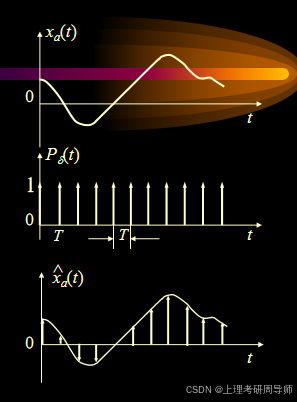
单位冲激函数

二、频谱的周期延拓

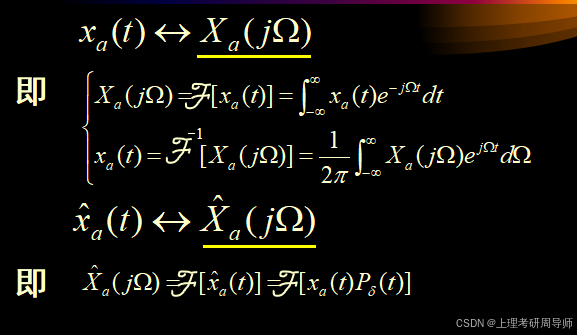
由于是周期函数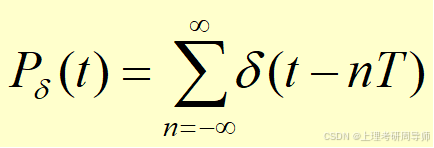

可用傅立叶级数表示，即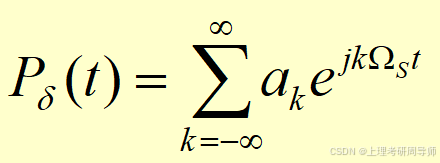

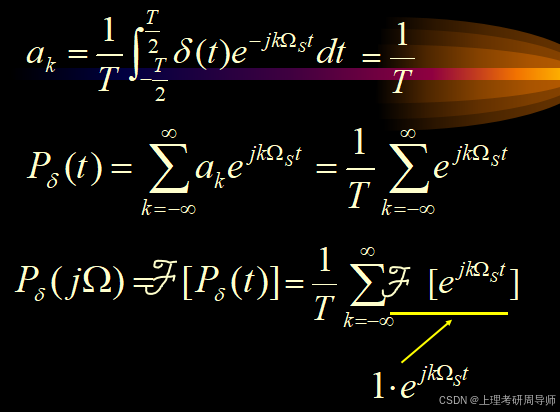
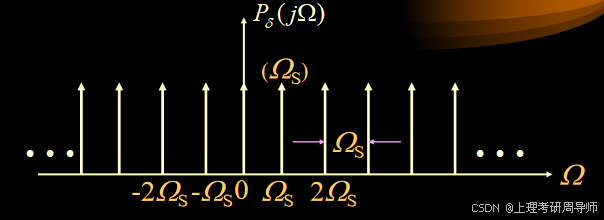
采样信号的傅氏变换为

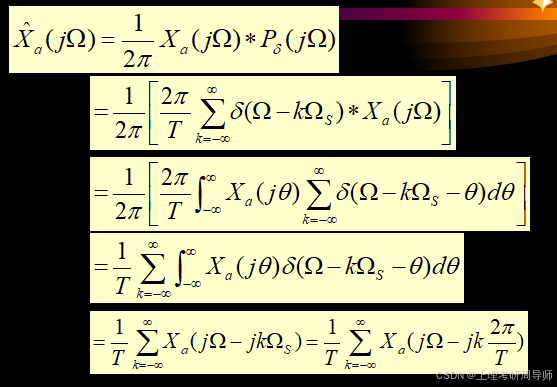
     采样信号的频谱是原模拟信号频谱的周期延拓，其延拓周期为Ω 。

讨论：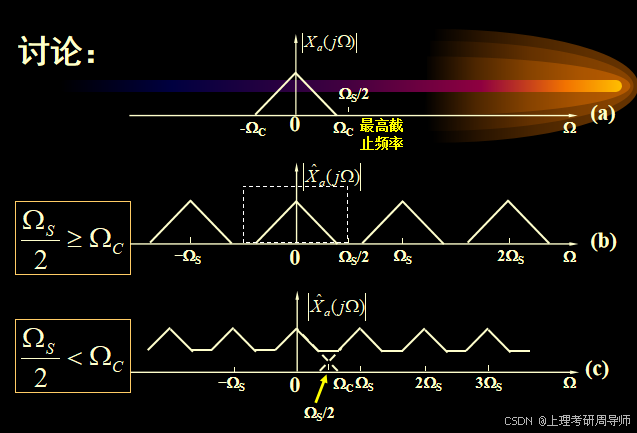 

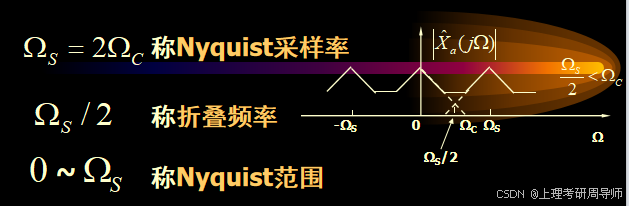
采样定理 ：

要想采样后能够不失真地还原出原信号，则采样频率必须大于两倍原信号频谱的最高截止频率（s2C）。

由上面的分析有，频谱发生混叠的原因有两个：

1.采样频率低

2.连续信号的频谱没有被限带

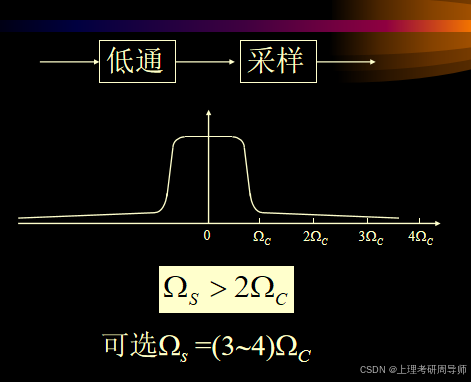
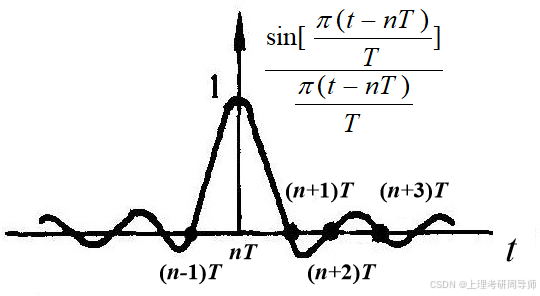
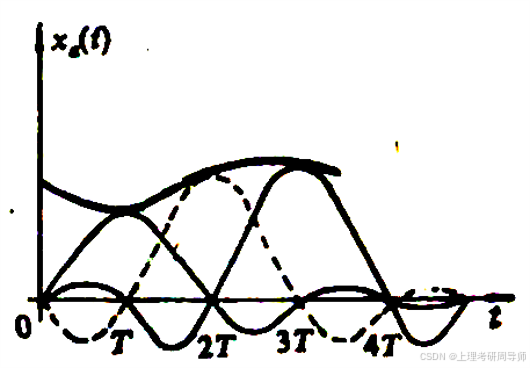
1.4.2 采样的恢复

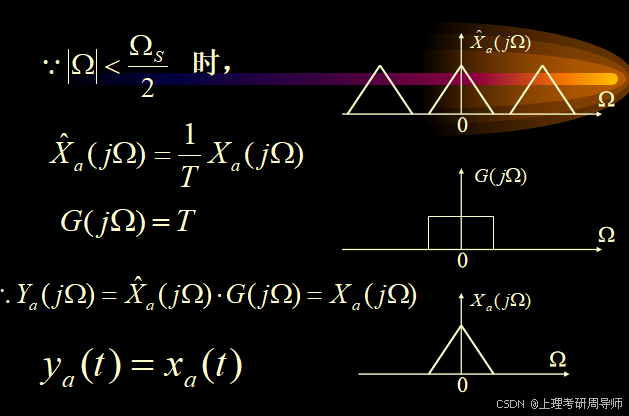
时域分析

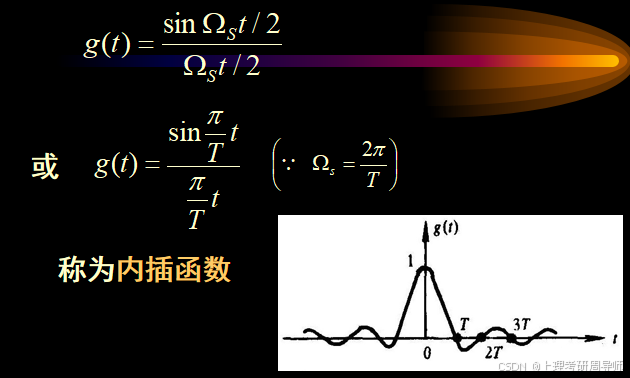
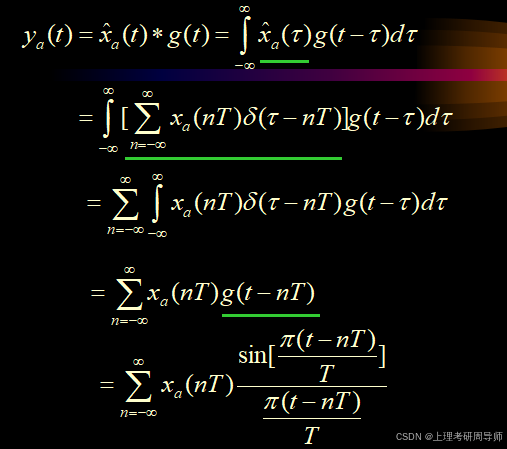
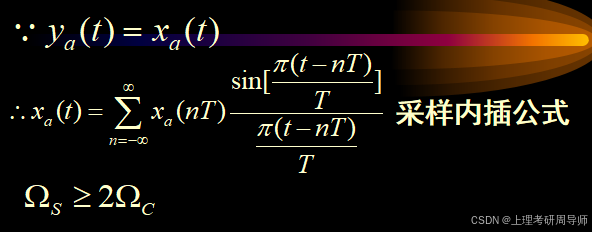
   采样内插公式说明：只要满足采样频率高于两倍信号最高截止频率，则整个连续时间信号就可以用它的采样值来完全代表，而不会丢失任何信息。