图

1. 图的基本概念

树是特殊的图，对于图来说，树是一种无环的连通图。对于树来说，我们通常使用树的节点来存储数据，主要关系树的节点；但对于图来说，我们通常研究节点与节点（边）的连接关系。

1.1 完全图

在 $n$ 个顶点的无向图中，若有 $\frac{n(n-1)}{2}$ 条边，即任意两个顶点有且只有一条边，则此图为完全图。

在 $n$ 个顶点的有向图中，若有 $n(n-1)$ 条边，即任意两个顶点有且仅有方向相反的边，则此图为有向完全图。

1.2 邻接顶点

在无向图中，若 $(u,v)$ 是 $\mathrm{E}(\mathrm{G})$ 中的一条边，则称 $u$ 和 $v$ 互为邻接顶点，并称边 $(u,v)$ 依附于顶点 $u$ 和 $v$ 。

在有向图中，若 $\text{<}u,v\text{>}$ 是 $\mathrm{E}(\mathrm{G})$ 中的一条边，则称顶点 $u$ 邻接到 $v$ ，顶点 $v$ 邻接自顶点 $u$ ，并称边 $\text{<}u,v\text{>}$ 与顶点 $u$ 和 $v$ 相关联。

1.3 顶点的度

顶点的度是指与它相关联的边的个数，顶点的度等于该顶点的入度和出度之和。对于有向图，入度是指以顶点为终点的有向边的个数，出度是指以顶点为起点的有向边的个数（$\mathrm{dev}(\mathrm{v})=\mathrm{indev}(\mathrm{v})+\mathrm{outdev}(\mathrm{v})$）；对于无向图，入度与出度相等（$\mathrm{dev}(\mathrm{v})=\mathrm{indev}(\mathrm{v})=\mathrm{outdev}(\mathrm{v})$）。

1.4 路径

在图 $\mathrm{G}=(\mathrm{V},\mathrm{E})$ 中，若从顶点 $V_i$ 出发有一组边使其可以到达顶点 $V_j$ ，则称顶点 $V_i$ 到顶点 $V_j$ 的顶点序列，为顶点 $V_i$ 到顶点 $V_j$ 的路径。

对于不带权的图，一条路径的长度是指该路径上边的条数；对于带权图，一条路径的长度是指该路径上各个边权值的总和。

若一条路径上各顶点 $V_1,V_2,V_3,...,V_m$ 均不重复，则这样的路径称为简单路径；若路径上第一个顶点 $V_1$ 与最后一个顶点 $V_m$ 重合，则这样的路径称为回路或环。

1.5 连通图

在无向图中，若从顶点 $V_1$ 到顶点 $V_2$ 有路径，就称顶点 $V_1$ 与顶点 $V_2$ 是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

在有向图中，若每一对顶点 $V_i$ 和 $V_j$ 之间都存在一条从 $V_i $ 到 $V_j$ 的路径，也存在一条从 $V_j$ 到 $V_i$ 的路径，则称此图是强连通图。

2. 图的存储结构

图的存储方式主要有两种，邻接矩阵和邻接表。

2.1 邻接矩阵

邻接矩阵使用一个二维数组来表示图中各个节点之间的连接关系。对于一个包含 $n$ 个节点的图，邻接矩阵是一个 $n \times n $ 的矩阵，其中矩阵中的每个元素表示节点之间的边（可以是权重，也可以表示是否存在边）。

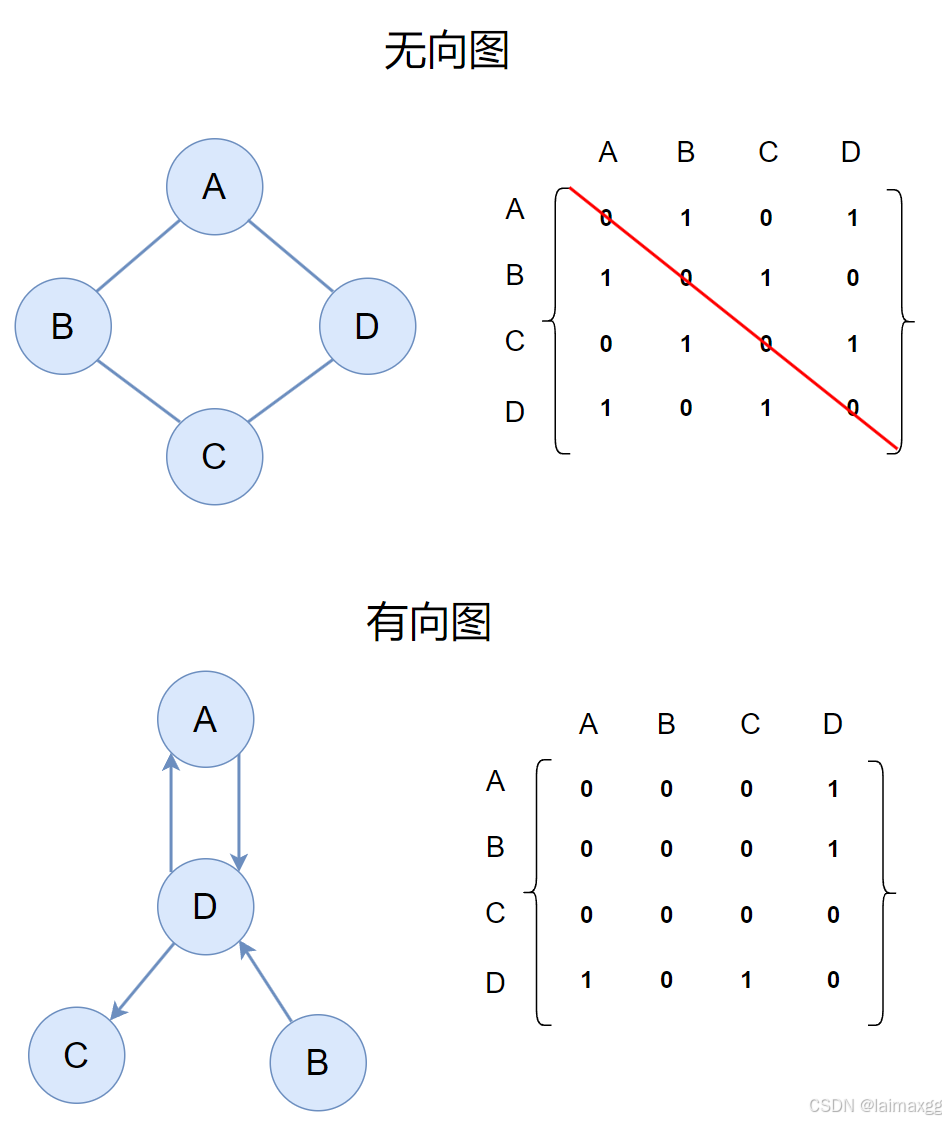
如果是带权图，矩阵内的值为权值。顶点与自身的权值为 0 ，如果两个顶点不通，它们的权值为 $\infty$。

2.1.1 邻接矩阵的优缺点

优点：

1. 实现简单，适合稠密图（边数接近于节点数平方的情况）。
2. 判断两个节点是否相邻非常高效，只需 $O(1)$ 时间复杂度。

缺点：

1. 空间复杂度较高，对于稀疏图来说会浪费大量内存。

2.1.2 代码实现

V 为图中数据的类型，W 为权值的类型（一般为 int）。

#include <vector>
#include <map>
#include <iostream>
using namespace std;

//邻接矩阵
template<class V,class W,W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
	typedef Graph<V, W, MAX_W, Direction> Self;
	Graph() = default;
	Graph(const V* vertexs, size_t n)
	{
		_vertexs.reserve(n);
		for (size_t i = 0; i < n; i++)
		{
			_vertexs.push_back(vertexs[i]);
			_vIndexMap[vertexs[i]] = i;
		}
		//用MAX_W表示无穷大
		_matrix.resize(n, vector<W>(n, MAX_W));
	}

	size_t GetVertexIndex(const V& v)
	{
		auto ret = _vIndexMap.find(v);
		if (ret != _vIndexMap.end())
		{
			return ret->second;
		}
		else
		{
			throw invalid_argument("不存在的顶点");
			return -1;
		}
	}

	void AddEdge(const V& src, const V& dest, const W& w)
	{
		size_t srci = GetVertexIndex(src);
		size_t desti = GetVertexIndex(dest);
		_matrix[srci][desti] = w;
		if (Direction == false)
		{
			_matrix[desti][srci] = w;
		}
	}

	void PrintMatrix() const
	{
		cout << "邻接矩阵：" << endl;
		for (const auto& row : _matrix)
		{
			for (const auto& weight : row)
			{
				if (weight == MAX_W)
					cout << "∞\t";  // 用 "∞" 表示无穷大
				else
					cout << weight << "\t";
			}
			cout << endl;
		}
	}

private:
	map<V, size_t> _vIndexMap;//快速查找顶点在邻接矩阵中的索引
	vector<V> _vertexs;		//顶点集合
	vector<vector<W>> _matrix;	//边的邻接矩阵
};

int main()
{
	Graph<char, int, INT_MAX, true> g("0123", 4);
	g.AddEdge('0', '1', 1);
	g.AddEdge('0', '3', 4);
	g.AddEdge('1', '3', 2);
	g.AddEdge('1', '2', 9);
	g.AddEdge('2', '3', 8);
	g.AddEdge('2', '1', 5);
	g.AddEdge('2', '0', 3);
	g.AddEdge('3', '2', 6);
	g.PrintMatrix();
}

2.2 邻接表

邻接表则为图中的每个节点维护一个链表或数组，使用链表表示边的关系。

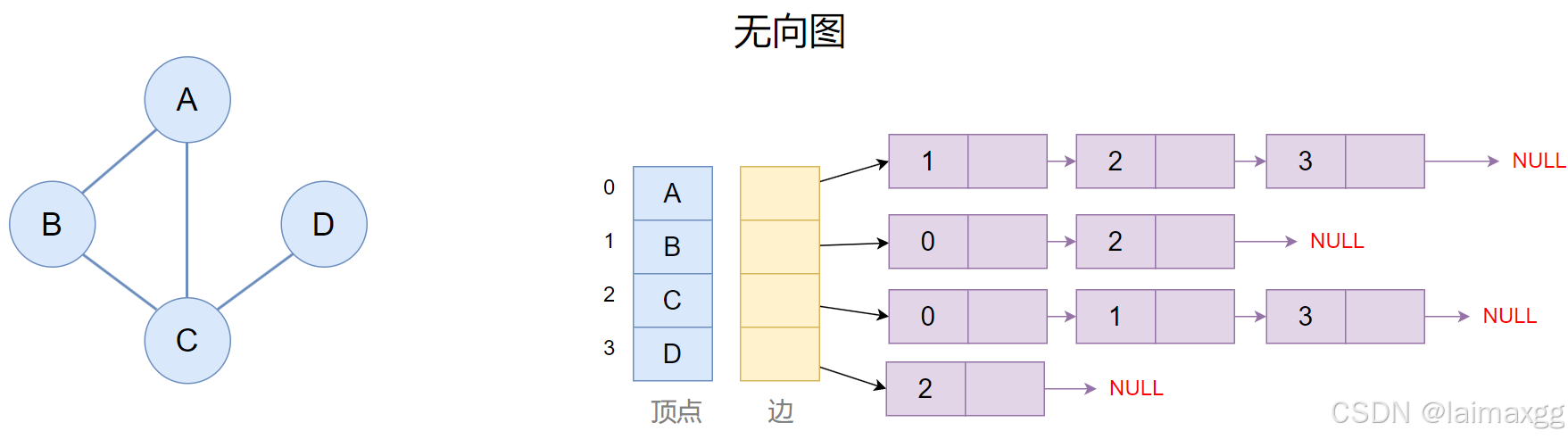
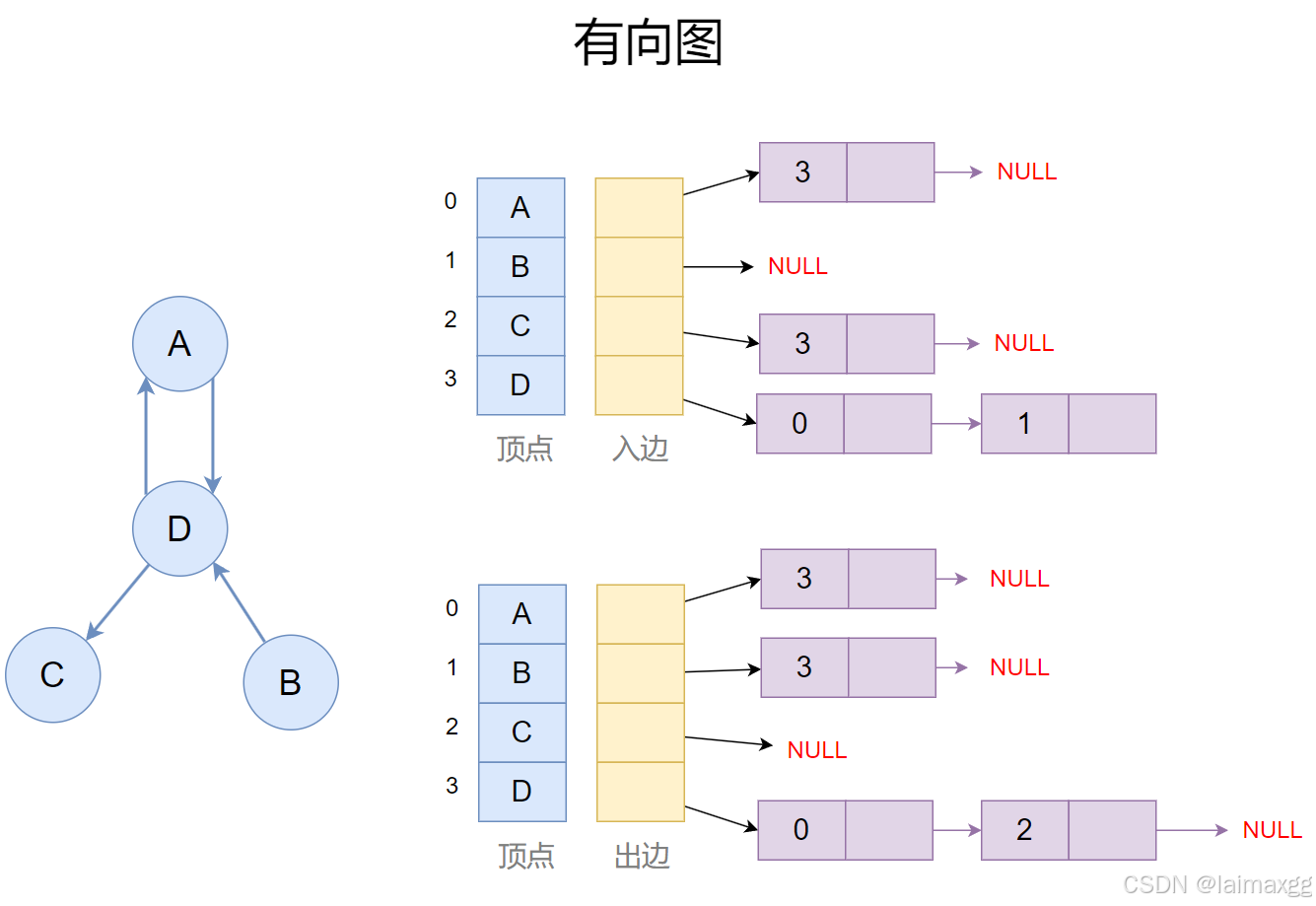
2.2.1 邻接表的优缺点

优点：

1. 空间效率高，特别适合稀疏图。
2. 存储结构灵活，可以方便地添加或删除边。

缺点：

1. 判断两个节点是否直接相邻可能需要遍历链表，最坏情况时间复杂度较高。

2.2.2 代码实现

代码实现中，邻接表节点的插入使用头插提高插入效率。有向图只实现了记录每个顶点的出边，实现入边需要增加一个邻接表。V 为图中数据的类型，W 为权值的类型（一般为 int）。

#include <vector>
#include <map>
#include <iostream>
#include <string>
using namespace std;

//邻接表
template<class W>
class LinkEdge
{
public:
	int _srcIndex;
	int _destIndex;
	W _w;
	LinkEdge<W>* _next;

	LinkEdge(const W& w):_srcIndex(-1),_destIndex(-1),_w(w),_next(nullptr)
	{}
};

template<class V, class W, bool Direction = false>
class Graph
{
public:
	typedef LinkEdge<W> Edge;
	Graph(const V* vertex,size_t n)
	{
		for (size_t i = 0; i < n; i++)
		{
			_vertexs.push_back(vertex[i]);
			_vIndexMap[vertex[i]] = i;
		}

		_tables.resize(n, nullptr);
	}

	size_t GetVertexIndex(const V& v)
	{
		auto ret = _vIndexMap.find(v);
		if (ret != _vIndexMap.end())
		{
			return ret->second;
		}
		else
		{
			throw invalid_argument("不存在的顶点");
			return -1;
		}
	}

	void AddEdge(const V& src, const V& dest, const W& w)
	{
		size_t srcIndex = GetVertexIndex(src);
		size_t destIndex = GetVertexIndex(dest);
		
		Edge* edge = new Edge(w);
		edge->_srcIndex = srcIndex;
		edge->_destIndex = destIndex;
		//头插
		edge->_next = _tables[srcIndex];
		_tables[srcIndex] = edge;

		if (Direction == false)
		{
			Edge* dest_edge = new Edge(w);
			dest_edge->_srcIndex = destIndex;
			dest_edge->_destIndex = srcIndex;
			dest_edge->_next = _tables[destIndex];
			_tables[destIndex] = dest_edge;
		}
	}

	void PrintGraph() const
	{
		for (size_t i = 0; i < _tables.size(); i++)
		{
			cout << _vertexs[i] << " -> ";
			Edge* p = _tables[i];
			while (p != nullptr)
			{
				cout << "[" << _vertexs[p->_destIndex] << ", " << p->_w << "] ";
				p = p->_next;
			}
			cout << endl;
		}
	}

private:
	map<string, int> _vIndexMap;//快速查找顶点在邻接矩阵中的索引
	vector<V> _vertexs;		//顶点集合
	vector<Edge*> _tables;	//邻接表
};

int main()
{
	string a[] = { "张三", "李四", "王五", "赵六" };
	Graph<string, int> g1(a, 4);
	g1.AddEdge("张三", "李四", 100);
	g1.AddEdge("张三", "王五", 200);
	g1.AddEdge("王五", "赵六", 30);
	g1.PrintGraph();
}

3. 图的遍历

图的遍历分为深度优先遍历（DFS）和广度优先遍历（BFS）。两者的区别是，深度优先遍历会沿着一条路径走到头，再回过来遍历没有经过的顶点；广度优先遍历会先遍历与一个顶点连接的所有顶点，再深入其他顶点遍历没有遍历过的顶点。

需要注意的是，无论是深度优先遍历还是广度优先遍历，只有连通图才能一次遍历到所有的顶点。所以，也可以通过深度优先遍历和广度优先遍历找出哪些顶点不连通。

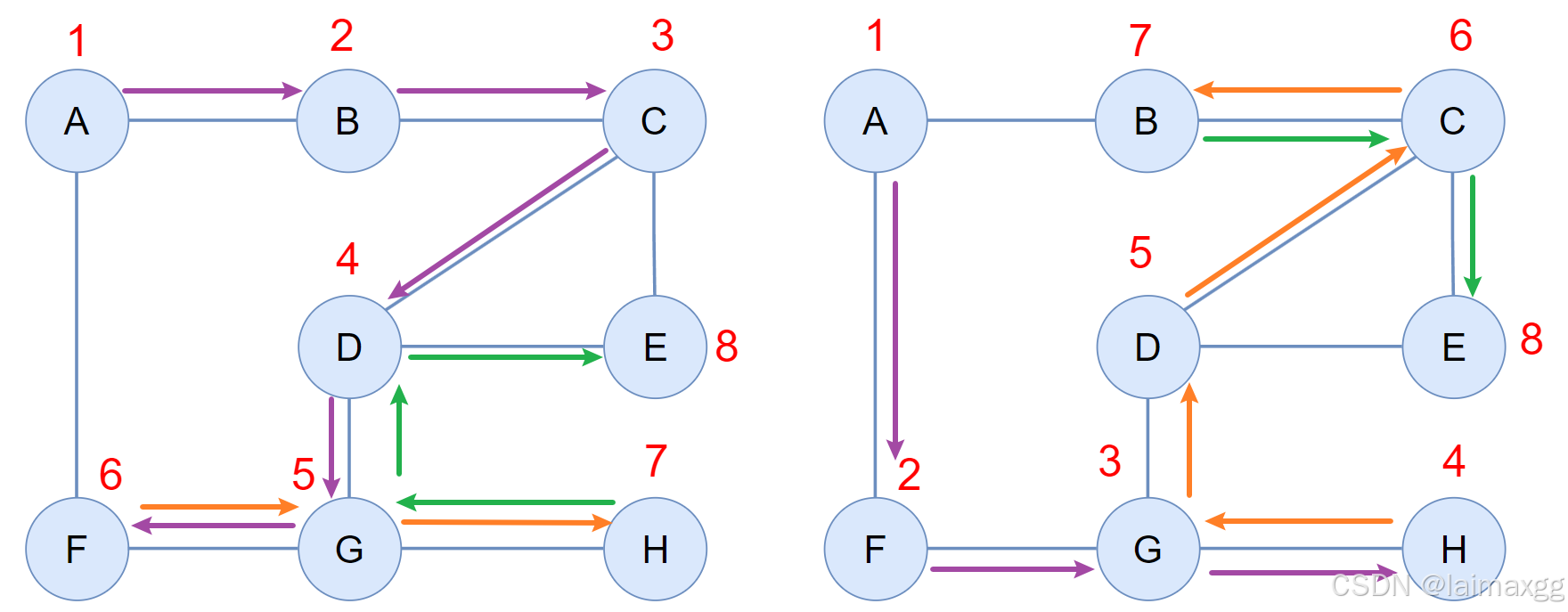
3.1 深度优先遍历（DFS）

深度优先搜索通过不断向前探索，直到无法继续为止，然后回溯寻找其他路径。深度优先的遍历结果不是唯一的，当一个顶点连接多个顶点时，道路的分叉会导致遍历出现不同的结果：

3.1.1 代码实现

邻接矩阵实现：

//...
void _DFS(const V& v, vector<bool>& isvisted)
	{
		cout << v << " ";
		int index = GetVertexIndex(v);
		for (int i = 0; i < _vertexs.size(); i++)
		{
			if (_matrix[index][i]!= MAX_W && !isvisted[i])
			{
				isvisted[i] = true;
				_DFS(_vertexs[i],isvisted);
			}
		}
	}

	void DFS(const V& v)
	{
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过
		int index = GetVertexIndex(v);
		isvisted[index] = true;
		_DFS(v, isvisted);
	}
//...
int main()
{
	string a[] = { "A", "B", "C", "D" ,"E","F","G","H" };
	Graph<string, int> g1(a, 8);
	g1.AddEdge("A", "B", 10);
	g1.AddEdge("A", "F", 20);
	g1.AddEdge("B", "C", 30);
	g1.AddEdge("C", "D", 40);
	g1.AddEdge("C", "E", 50);
	g1.AddEdge("D", "E", 60);
	g1.AddEdge("D", "G", 70);
	g1.AddEdge("G", "H", 80);
	g1.AddEdge("G", "F", 90);

	g1.DFS("A");
}

---

邻接表实现：

//...
void _DFS(int index, vector<bool>& isvisted)
{
	isvisted[index] = true;
	cout << _vertexs[index] << " ";
	Edge* edge = _tables[index];
	while (edge)
	{
		if (!isvisted[edge->_destIndex])
		{
			_DFS(edge->_destIndex, isvisted);
		}
		edge = edge->_next;
	}
}

void DFS(const V& v)
{
	vector<bool> isvisted(_vertexs.size(), false);
	int index = GetVertexIndex(v);
	_DFS(index, isvisted);
}
//...
int main()
{
	string a[] = { "A", "B", "C", "D" ,"E","F","G","H" };
	Graph<string, int> g1(a, 8);
	g1.AddEdge("A", "B", 10);
	g1.AddEdge("A", "F", 20);
	g1.AddEdge("B", "C", 30);
	g1.AddEdge("C", "D", 40);
	g1.AddEdge("C", "E", 50);
	g1.AddEdge("D", "E", 60);
	g1.AddEdge("D", "G", 70);
	g1.AddEdge("G", "H", 80);
	g1.AddEdge("G", "F", 90);

	g1.DFS("A");
}

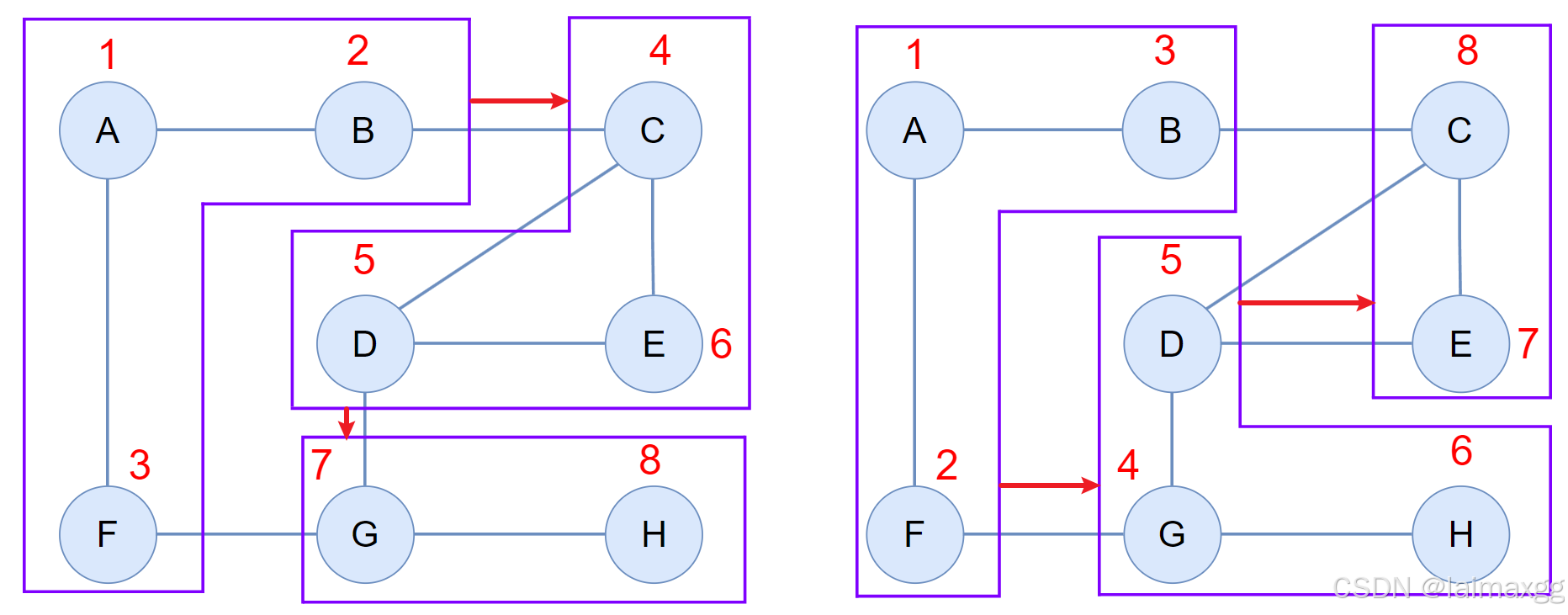
3.2 广度优先遍历（BFS）

广度优先遍历以层次方式逐步展开所有可能的邻居节点。广度优先遍历的结果不是唯一的，当一个顶点连接多个顶点时，道路的分叉会导致遍历出现不同的结果：

3.2.1 代码实现

邻接矩阵实现：

//....
void BFS(const V& src)
	{
		size_t srcindex = GetVertexIndex(src);
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过

		queue<int> q;
		q.push(srcindex);
		isvisted[srcindex] = true;
		size_t d = 1;
		size_t dsize = 1;
		while (!q.empty())
		{
			dsize = q.size();
			cout << "Level"<<d<<": ";
			while (dsize--)
			{
				size_t front = q.front();
				q.pop();
				for (size_t i = 0; i < _vertexs.size(); i++)
				{
					if (isvisted[i] == false && _matrix[front][i] != MAX_W)
					{
						cout<< "["<<_vertexs[i] << ":" << _matrix[front][i]<<"]";
						isvisted[i] = true;
						q.push(i);
					}
				}
			}
			cout << endl;
			d++;
		}
	}
//....

int main()
{
	string a[] = { "A", "B", "C", "D" ,"E","F","G","H" };
	Graph<string, int> g1(a, 8);
	g1.AddEdge("A", "B", 10);
	g1.AddEdge("A", "F", 20);
	g1.AddEdge("B", "C", 30);
	g1.AddEdge("C", "D", 40);
	g1.AddEdge("C", "E", 50);
	g1.AddEdge("D", "E", 60);
	g1.AddEdge("D", "G", 70);
	g1.AddEdge("G", "H", 80);
    g1.AddEdge("G", "F", 90);

	g1.BFS("A");
}

---

邻接表实现：

//...
void BFS(const V& v)
	{
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过
		queue<int> q;
		int index = GetVertexIndex(v);
		q.push(index);
		isvisted[index] = true;
		while (!q.empty())
		{
			int currentIndex = q.front();
			q.pop();

			cout << _vertexs[currentIndex] << " ";
			Edge* edge = _tables[currentIndex];
			while (edge)
			{
				if (!isvisted[edge->_destIndex])
				{
					q.push(edge->_destIndex);
					isvisted[edge->_destIndex] = true;
				}
				edge = edge->_next;
			}
		}
	}
//...

4. 图的算法

4.1 最小生成树

对于一个无向连通图，最小生成树是包含图中所有顶点且边权和最小的树。它不仅保证了图的连通性，而且在众多可能的生成树中，所选边的权值总和是最低的。即，从生成树中删去任何一条边，生成树都不再连通；反之，增加任何一条边，都会形成一条回路。

• 特性： 若连通图由 $n$ 个顶点组成，则生成树必包含 $n$ 个顶点和 $n-1$ 条边。

构造最小生成树的算法有Kruskal算法和Prim算法，两者都是采用逐步求解的贪心策略。

4.1.1 Kruskal算法

Kruskal算法适合稀疏图的情况。

算法过程：

1. 给定一个有 $n$ 个顶点的连通网络 N = { V , E } \rm N=\{V,E\} N={V,E} 。
2. 创建一个同样有 $n$ 个顶点，但不包含边的图 G = { V , N U L L } \rm G=\{V,NULL\} G={V,NULL} 。
3. 选取出 $\mathrm{N}$ 中当前权值最小的边，在 $\mathrm{G}$ 中连通对应的顶点。
4. 重复 3 的操作，但 $\mathrm{G}$ 中不能产生回路，直到所有顶点都被连通。

图示：

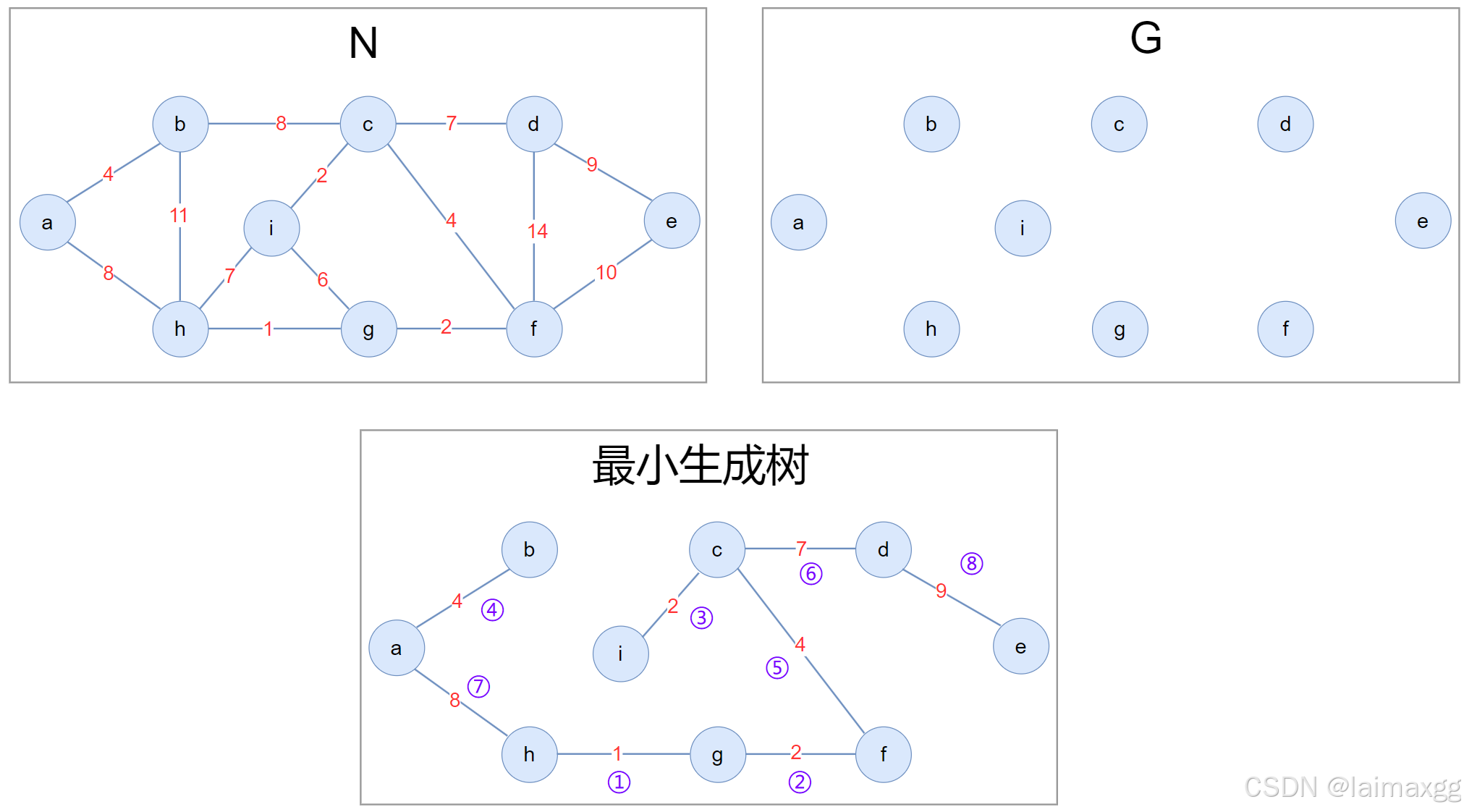
本图重绘《算法导论》中 Kruskal 算法的算法流程。

在第 ⑥ 步中，(i,g) 的边的权值更小，但连接会产生回路，于是选择权值第二小的 (c,g) 连接。

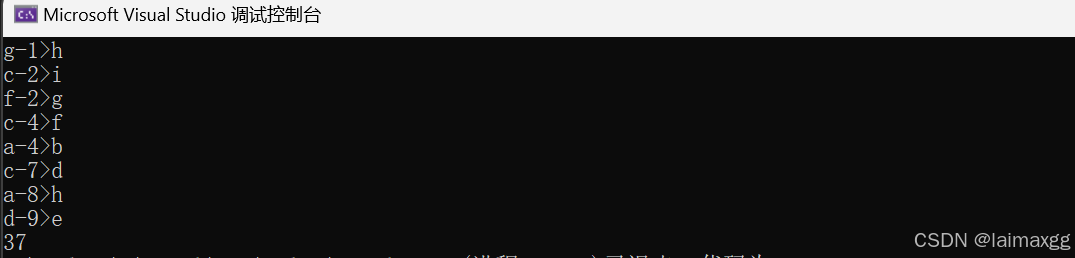
4.1.1.1 代码实现

在实现Kruskal算法时，我们需要使用到优先队列（priority_queue），优先队列的第一个元素总是队列中最大（或最小）的元素，方便我们快速地找出权值最小的边；我们还需要使用到并查集（UnionFinSet），用于查询某个顶点是否已经在生成树中，以此来避免产生回路。代码使用邻接矩阵实现：

#include <vector>
#include <map>
#include <iostream>
#include <queue>
using namespace std;

class UnionFindSet
{
public:
	UnionFindSet(size_t size) :_ufs(size, -1) {}

	int FindRoot(int index)
	{
		if (_ufs[index] < 0)
		{
			return index;
		}
		return _ufs[index] = FindRoot(_ufs[index]);
	}

	bool Union(int x, int y)
	{
		int root1 = FindRoot(x);
		int root2 = FindRoot(y);

		//如果两个元素本就在同一个集合返回false
		if (root1 == root2)
		{
			return false;
		}

		//按秩合并，将较矮的树合并到较高的树下
		//由于用负数表示秩，值越小树的高度越高
		if (_ufs[root1] > _ufs[root2])
			swap(root1, root2);

		// 将集合 root2 合并到 root1 上
		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
		return true;
	}

	int Count()
	{
		int count = 0;
		for (auto it : _ufs)
		{
			if (it < 0)
			{
				count++;
			}
		}
		return count;
	}

	bool InSet(int x, int y)
	{
		return FindRoot(x) == FindRoot(y);
	}

private:
	vector<int> _ufs;
};

//...
struct Edge
{
	size_t _srci;
	size_t _desti;
	W _w;

	Edge(size_t srci,size_t desti,const W& w):_srci(srci),_desti(desti),_w(w){}

	bool operator>(const Edge& e) const
	{
		return _w > e._w;
	}
};

W Kruskal(Self& minTree)
{
	minTree._vertexs = _vertexs;
	minTree._vIndexMap = _vIndexMap;
	minTree._matrix.resize(_vertexs.size());
	for (auto& it : minTree._matrix)
	{
		it.resize(_vertexs.size(), MAX_W);
	}

	priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
	for (size_t i = 0; i < _vertexs.size(); i++)
	{
		for (size_t j = 0; j < _vertexs.size(); j++)
		{
			if (i < j && _matrix[i][j] != MAX_W)
			{
				minque.push(Edge(i, j, _matrix[i][j]));//minque的第一个元素总是权值最小的边
			}
		}
	}

	int size = 0;
	W totalW = W();
	UnionFindSet ufs(_vertexs.size());
	while (!minque.empty())
	{
		Edge min = minque.top();
		minque.pop();
		if (!ufs.InSet(min._srci, min._desti))
		{
			minTree.AddEdge(_vertexs[min._srci], _vertexs[min._desti], min._w);
			cout << _vertexs[min._srci] << "-" << min._w << ">" << _vertexs[min._desti] << endl;
			ufs.Union(min._srci, min._desti);
			size++;
			totalW += min._w;
		}
	}
	if (size == _vertexs.size() - 1)
	{
		//如果能够构建最小生成树
		return totalW;
	}
	else
	{
		return W();
	}
}
//...
int main()
{
	string a[] = { "a", "b", "c", "d" ,"e","f","g","h","i"};
	Graph<string, int> g1(a, 9);
	g1.AddEdge("a", "b", 4);
	g1.AddEdge("b", "h", 11);
	g1.AddEdge("a", "h", 8);
	g1.AddEdge("b", "c", 8);
	g1.AddEdge("c", "d", 7);
	g1.AddEdge("c", "i", 2);
	g1.AddEdge("d", "e", 9);
	g1.AddEdge("d", "f", 14);
	g1.AddEdge("e", "f", 10);
	g1.AddEdge("f", "g", 2);
	g1.AddEdge("f", "c", 4);
	g1.AddEdge("g", "i", 6);
	g1.AddEdge("g", "h", 1);
	g1.AddEdge("h", "i", 7);

	Graph<string, int> minTree;
	cout<< g1.Kruskal(minTree);
}

4.1.2 Prim算法

Prim 算法在处理密集图时通常表现更好。

算法过程：

1. 给定一个有 $n$ 个顶点的连通网络 N = { V , E } \rm N=\{V,E\} N={V,E}。
2. 创建一个同样有 $n$ 个顶点，但不包含边的图 G = { V , N U L L } \rm G=\{V,NULL\} G={V,NULL} 。任意选取一个顶点作为生成树的根。
3. 选取已加入到生成树中的顶点集合中，与未加入到生成树中的顶点集合中，权值最小的边相连，新连接的节点加入到生成树中。
4. 重复 3 的操作，但 $\mathrm{G}$ 中不能产生回路，直到所有顶点都被加入到生成树中。

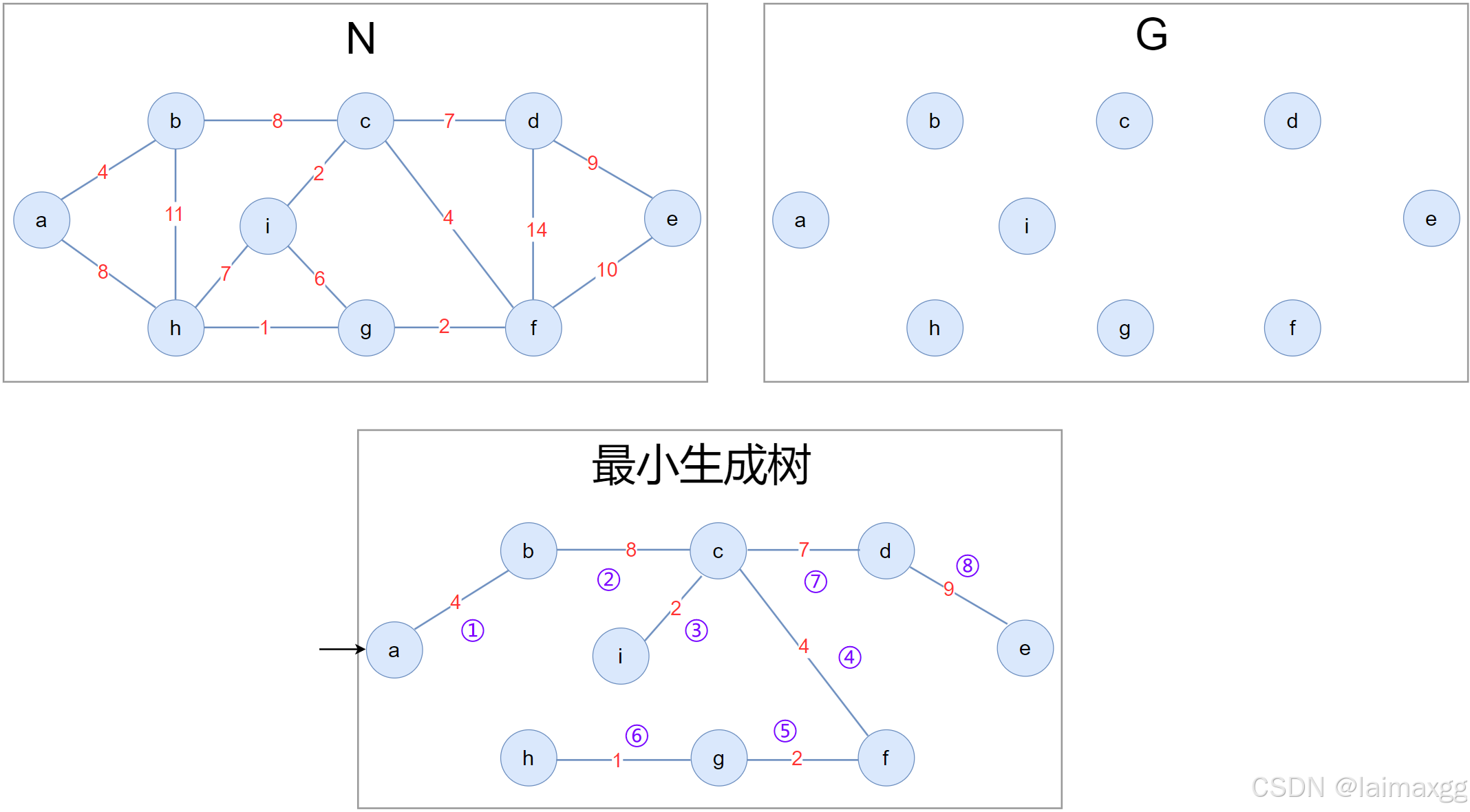
本图重绘《算法导论》中 Prim 算法的算法流程。

4.1.2.1 代码实现

//...
W Prim(Self& minTree,const V& src)
	{
		minTree._vertexs = _vertexs;
		minTree._vIndexMap = _vIndexMap;
		minTree._matrix.resize(_vertexs.size());
		for (auto& it : minTree._matrix)
		{
			it.resize(_vertexs.size(), MAX_W);
		}

		size_t srci = GetVertexIndex(src);

		//用inTree存储在生成树中的顶点
		vector<bool> inTree(_vertexs.size(), false);
		inTree[srci] = true;

		priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			if (_matrix[srci][i] != MAX_W)
			{
				minque.push(Edge(srci, i, _matrix[srci][i]));//先将根节点所有的边放入优先队列中
			}
		}
		size_t size = 0;
		W totalW = W();
		while (!minque.empty())
		{
			Edge min = minque.top();
			minque.pop();

			//如果最小边在X里，连接会构成环
			if (inTree[min._desti])
			{
				continue;
			}
			else
			{
				minTree.AddEdge(_vertexs[min._srci], _vertexs[min._desti], min._w);
				cout << _vertexs[min._srci] << "-" << min._w << ">" << _vertexs[min._desti] << endl;
				inTree[min._desti] = true;
				size++;
				totalW += min._w;

				if (size == _vertexs.size() - 1)
				{
					//如果最小生成树构建完，退出循环
					break;
				}
				for (size_t i = 0; i < _vertexs.size(); i++)
				{
					if (_matrix[min._desti][i] != MAX_W && !inTree[i])
					{
						//将新连接的顶点放入最小生成树中
						minque.push(Edge(min._desti, i, _matrix[min._desti][i]));
					}
				}
			}
		}
		if (size == _vertexs.size() - 1)
		{
			return totalW;
		}
		else
		{
			return W();
		}
	}
//...

int main()
{
	string a[] = { "a", "b", "c", "d" ,"e","f","g","h","i"};
	Graph<string, int> g1(a, 9);
	g1.AddEdge("a", "b", 4);
	g1.AddEdge("b", "h", 11);
	g1.AddEdge("a", "h", 8);
	g1.AddEdge("b", "c", 8);
	g1.AddEdge("c", "d", 7);
	g1.AddEdge("c", "i", 2);
	g1.AddEdge("d", "e", 9);
	g1.AddEdge("d", "f", 14);
	g1.AddEdge("e", "f", 10);
	g1.AddEdge("f", "g", 2);
	g1.AddEdge("f", "c", 4);
	g1.AddEdge("g", "i", 6);
	g1.AddEdge("g", "h", 1);
	g1.AddEdge("h", "i", 7);

	Graph<string, int> minTree;
	cout<< g1.Prim(minTree,"a");
}

4.2 最短路径

最短路径名字非常直白，就是从一个顶点出发，找出到其他顶点的最短路径。最短路径的典型算法有三个，Dijkstra 算法、Bellman-Ford 算法、Floyd-Warshall 算法，它们之间的异同如下表格：

算法	算法用途	处理负权边	检测负权回路	时间复杂度	算法类型
Dijkstra	单源最短路径	❌	❌	$O(n^2)$ 或 $O((n+m)\log n)$ (使用堆优化)	贪心策略 + 逐步扩展
Bellman-Ford	单源最短路径	✅	✅	$O(nm)$ （普遍比 Dijkstra 要差）	松弛操作 + 动态规划
Floyd-Warshall	多源最短路径	✅	❌	$O(n3)$	动态规划

单源最短路径 ： 指计算某个顶点到所有顶点的最短路径。

多源最短路径： 指计算任意两个顶点之间的最短路径。

时间复杂度： m 表示图中边的个数。注意，下面给出的三种算法的代码实现都是基于邻接矩阵实现的。

4.2.1 Dijkstra算法

Dijkstra 算法是求解最短路径的经典算法，这个算法只适用于权值为正数的情况，Dijkstra 的算法原理为相对高效的贪心算法。

算法过程：

1. 确定源顶点 src，将其他顶点到 src 的距离初值设置为 $\infty$ 。
2. 更新与 src 相邻的顶点的距离，并选出顶点 u 为与 src 最近的顶点。
3. 更新与 u 相邻的顶点的距离，并选出从 src 经过 u 到该顶点最近的顶点为新的 u。
4. 重复 3 直到所有的顶点的最短路径都被确定。

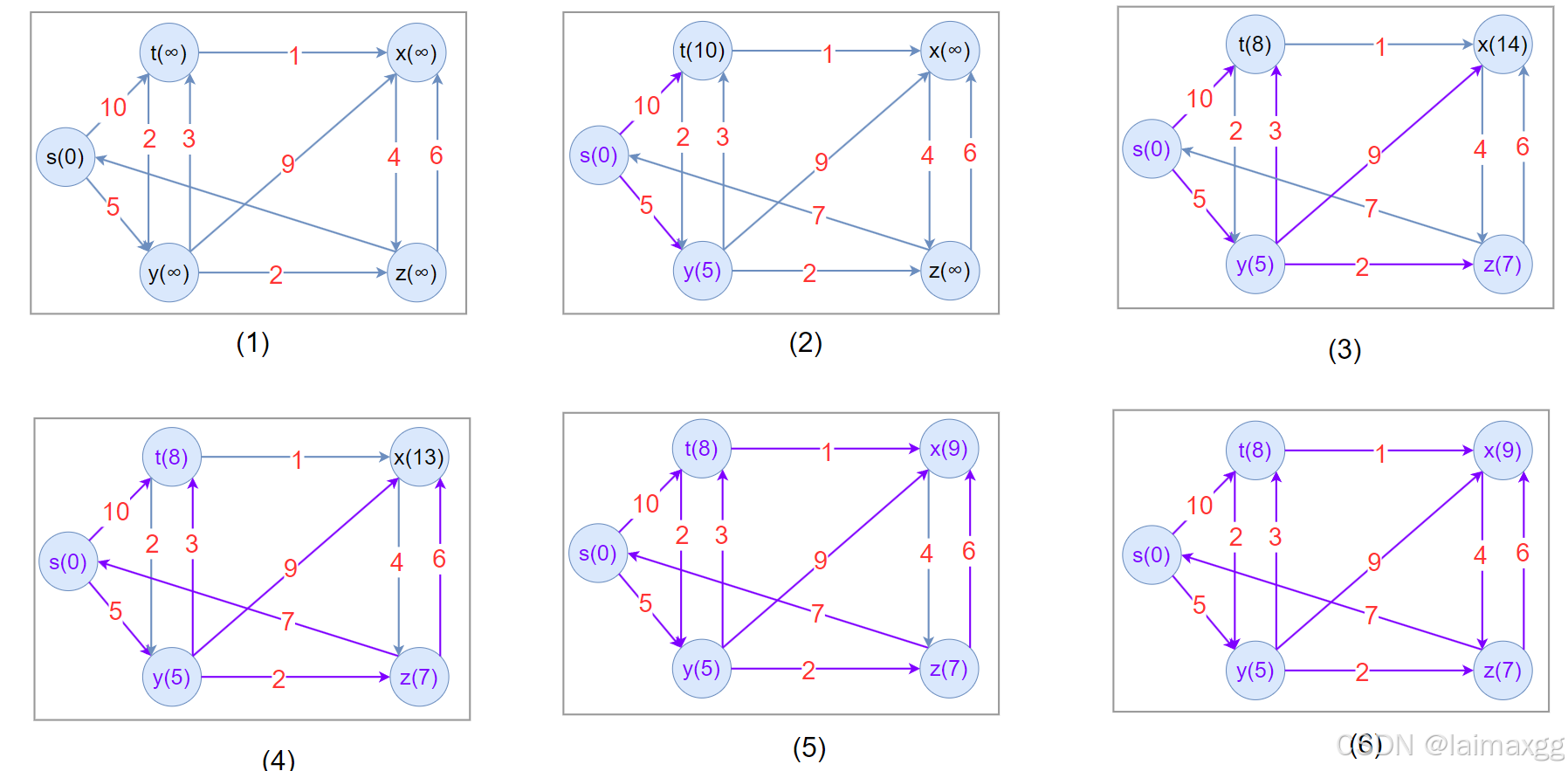
本图重绘《算法导论》中 Dijkstra 算法的算法流程。字体颜色为紫色的顶点为最短路径确定的顶点。

代码实现

vector<int> dist 保存从源顶点到各个顶点的最短路径长度，初始时所有顶点的距离设为无穷大；vector<int> parentPath 保存每个顶点在最短路径上的前驱顶点，初始时全部设为 -1；vector<bool> confirm 存储已确定最短路径的顶点；

//...
void Dijstra(const V& src)
	{
		vector<int> dist(_vertexs.size(), MAX_W);
		vector<int> parentPath(_vertexs.size(), MAX_W);
		size_t srci = GetVertexIndex(src);

		vector<bool> confirm(_vertexs.size(), false);//存储已确定最短路径的顶点
		dist[srci] = W();//源点的最短路径是最小值

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			W min = MAX_W;	//最短路径，初值为最大值
			size_t u = srci;

			//遍历当前顶点的最小的边，更新符合条件的最短路径
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (confirm[j] == false && dist[j] < min)
				{
					min = dist[j];
					u = j;
				}
			}

			confirm[u] = true;	//顶点u的最短路径确定

			//遍历顶点 u 相邻的所有顶点，查找能够更新最短路径的顶点
			for (size_t k = 0; k < _vertexs.size(); k++)
			{
				//如果顶点k没有确定最短路径，且u和k相邻，且此时从源点到u的距离加上u到k的距离小于此时k的最短路径
				if (confirm[k] == false && _matrix[u][k] != MAX_W && dist[u] + _matrix[u][k]<dist[k])
				{
					cout << _vertexs[k] << "的最短路径由 " << dist[k] << " 更新为 " << dist[u] + _matrix[u][k] << endl;
					dist[k] = dist[u] + _matrix[u][k];
					parentPath[k] = u;
				}
			}
		}
	}
//...

int main()
{
	const char* str = "syztx";
	Graph<char, int,INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 10);
	g.AddEdge('s', 'y', 5);
	g.AddEdge('y', 't', 3);
	g.AddEdge('y', 'x', 9);
	g.AddEdge('y', 'z', 2);
	g.AddEdge('z', 's', 7);
	g.AddEdge('z', 'x', 6);
	g.AddEdge('t', 'y', 2);
	g.AddEdge('t', 'x', 1);
	g.AddEdge('x', 'z', 4);
	g.Dijstra('s');

}

4.2.2 Bellman-Ford算法

Bellman-Ford 算法可以用于解决负权图的单源最短路径问题，而且可以用来判断是否有负权回路。

注意，无论哪种最短路径算法，负权回路都是无法求出最短路径的。负权回路会导致最短路径无法定义（因为可以无限变短）。Dijkstra 算法可能得出错误结果，而 Bellman-Ford 算法能够正确检测到负权回路，但不会返回最短路径。

算法过程：

1. 确定源顶点 src，将其他顶点到 src 的距离初值设置为 $\infty$。
2. 对所有边 $(u,v,w)$ 进行松弛（即更新 $d[v]$）：如果 $d[u]+w<d[v]$ ，则更新 $d[v]=d[u]+w$。
3. 重复 2 $N-1$ 次（N 为顶点的个数），或重复直到不能更新最短路径。
4. 再次遍历所有边，判断有无负权回路。

本图重绘《算法导论》中 Bellman-Ford 算法的算法流程。紫色的边为进行最短路径更新时所选的边，图 (5) 中更新的是 -4 这条边。

4.2.2.1 代码实现

Bellman-Ford 算法的一个问题是，在更新顶点的最短路径的过程中，所有顶点的最短路径都不是确定的，有可能后更新的顶点，影响了早先更新顶点的最短路径，导致所有最短路径都要更新一次，Bellman-Ford 算法的主要问题就是在什么时候停止更新，这里我们选择使用一个 bool exchange 变量来判断是否发生更新，避免每次都要遍历 N-1 次（N 为顶点的个数）才能求出最短路径。

//...
bool BellmanFord(const V& src)
	{
		vector<int> dist(_vertexs.size(), MAX_W);
		vector<int> parentPath(_vertexs.size(), MAX_W);
		size_t srci = GetVertexIndex(src);
		dist[srci] = W();	//源点的最短路径为最小值

		for (size_t k = 0; k < _vertexs.size() - 1; k++)
		{
			bool exchange = false;//用于判断是否有最短路径发生更新
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
					{
						cout << _vertexs[j] << "的最短路径由 " << dist[j] << " 更新为 " << dist[i] + _matrix[i][j] << endl;
						//源点到i+i到j<源点到j，就更新最短路径
						dist[j] = dist[i] + _matrix[i][j];
						parentPath[j] = i;
						exchange = true;
					}
				}
			}
			if (exchange == false)
			{
				break;
			}
		}

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				//检查是否有负权回路
				if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					//最短路径求完，但有从源点到i+i到j<从源点到j，说明存在负权回路
					return false;
				}
			}
		}
		return true;
	}
//...
int main()
{
	const char* str = "syztx";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 6);
	g.AddEdge('s', 'y', 7);
	g.AddEdge('y', 'z', 9);
	g.AddEdge('y', 'x', -3);
	g.AddEdge('z', 's', 2);
	g.AddEdge('z', 'x', 7);
	g.AddEdge('t', 'y', 8);
	g.AddEdge('t', 'x', 5);
	g.AddEdge('t', 'z', -4);
	g.AddEdge('x', 't', -2);
	g.BellmanFord('s');

}

4.2.3 Floyd-Warshall算法

Floyd-Warshall 算法从功能上看，与 Dijkstra 算法和 Bellman-Ford 算法的不同是，Floyd-Warshall 算法计算的是多源最短路径，即它能够计算任意两个顶点的最短路径。Floyd-Warshall 算法的关键是思想是通过中间顶点去更新最短路径。

算法过程：

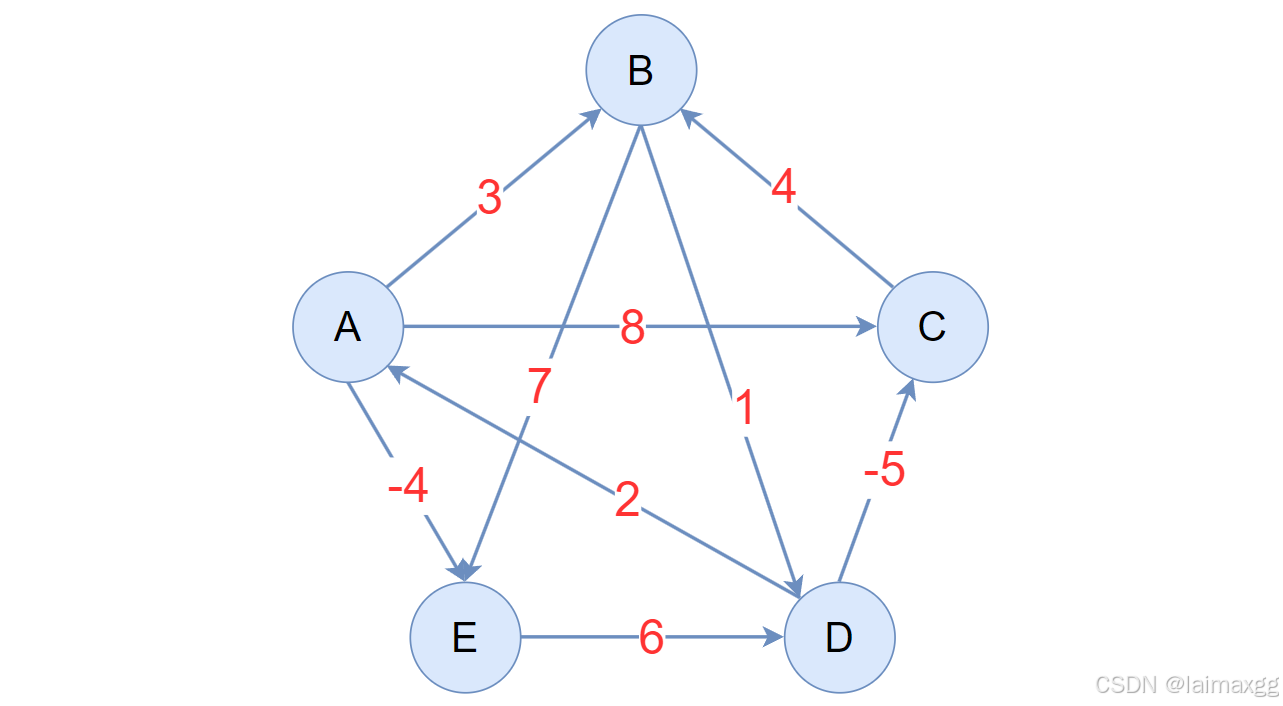
本图重绘《算法导论》中 Floyd-Warshall 算法的算法流程。为了方便理解，将顶点的值由数字改成了字母。

{ 0 , 1 , 2 , 3 , 4 , 5 } \{0,1,2,3,4,5\} {0,1,2,3,4,5} 分别表示 { 开始 , A , B , C , D } \{开始,A,B,C,D\} {开始,A,B,C,D}

最终，$D^{(5)}$ 中的内容就是邻接矩阵内任意两个顶点的最短路径。

说明：

左边的 $D$ 矩阵为邻接矩阵，$D^n$ 的 $n$ 表示该矩阵的中间顶点。整个矩阵表示当前求得的对应两顶点，经过顶点 $n$ 的最短路径。在更新最短路径的过程中，，如果经过顶点 $n$ 的两顶点的最短路径更短，就在矩阵上更新，否则最短路径的值与前一个矩阵相同。

右边的矩阵 $P$ 为，对于任意顶点对 $(i,j)$，若存在一条最短路径，则 $P[i][j]$ 表示从 $i$ 到 j 的路径中 $j$ 的“前一个顶点”（即 $j$ 的直接前驱）；如果 $i$ 到 $j$ 没有路径或 $j$ 就是 $i$，则记作“ $–$ ”或空。

动态的Floyd-Warshall 算法过程可以参考 B 站上的这个视频→ 图-最短路径-Floyd(弗洛伊德)

4.2.3.1 代码实现

代码中的 std::showpos 用于让正数的 + 显示出来，是为了让矩阵打印出来更整齐而使用的。

#include <vector>
#include <map>
#include <iostream>
#include <queue>
#include <iomanip>
//...
void FloydWarshall()
	{
		vector<vector<W>> vvDist(_vertexs.size(), vector<int>(_vertexs.size(), MAX_W));
		vector<vector<int>> vvParentPath(_vertexs.size(), vector<int>(_vertexs.size(), 0));

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (_matrix[i][j] != MAX_W)
				{
					//初始化D(0)和P(0)矩阵的内容
					vvDist[i][j] = _matrix[i][j];
					vvParentPath[i][j] = i;
				}
				//这里用-1表示P矩阵中i到j没有路径或j就是i的情况
				else
				{
					//i到j没有路径
					vvParentPath[i][j] = -1;
				}
				if (i == j)
				{
					//j就是i
					vvDist[i][j] = 0;
					vvParentPath[i][j] = -1;
				}
			}
		}

		//打印矩阵变化过程
		std::cout << std::showpos;
		cout << "D(0):" << "           " << "P(0):" << endl;
		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (vvDist[i][j] == MAX_W)
				{
					cout<<" * ";
				}
				else
				{
					cout << vvDist[i][j] << " ";
				}
			}
			cout << "       ";
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				cout << vvParentPath[i][j] << " ";
			}
			cout << endl;
		}

		int n = 1;
		//k表示中间顶点
		for (size_t k = 0; k < _vertexs.size(); k++)
		{
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (vvDist[i][k] != MAX_W && vvDist[k][j]!=MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
					{
						//如果从i经过k到j的路径比当前从i到j的最短路径更短，就更新最短路径
						vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
						vvParentPath[i][j] = vvParentPath[k][j];
					}
				}
			}
			//打印矩阵变化过程
			cout << "====================================================" << endl;
			cout << "D(" << n << "):" << "           " << "P(" << n << "):" << endl;
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (vvDist[i][j] == MAX_W)
					{
						cout << " * ";
					}
					else
					{
						cout << vvDist[i][j] << " ";
					}

				}
				cout << "       ";
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					cout << vvParentPath[i][j] << " ";
				}
				cout << endl;
			}
			n++;
		}
	}
//...

int main()
{
	string a[] = { "A", "B", "C", "D" ,"E" };
	Graph<string, int, INT_MAX, true> g1(a, 5);
	g1.AddEdge("A", "B", 3);
	g1.AddEdge("A", "E", -4);
	g1.AddEdge("A", "C", 8);
	g1.AddEdge("B", "E", 7);
	g1.AddEdge("B", "D", 1);
	g1.AddEdge("C", "B", 4);
	g1.AddEdge("D", "C", -5);
	g1.AddEdge("D", "A", 2);
	g1.AddEdge("E", "D", 6);

	g1.FloydWarshall();

}

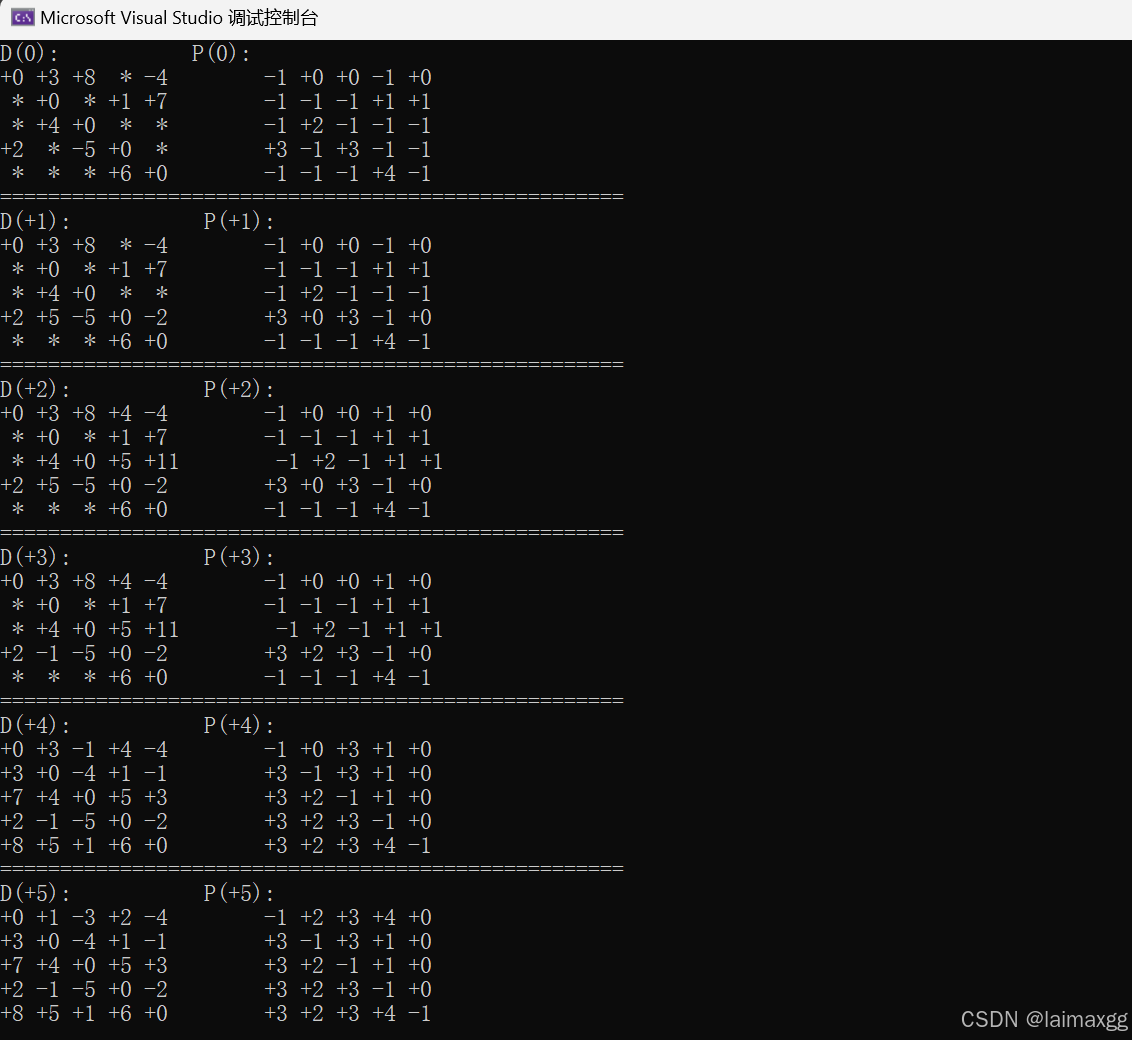
P 矩阵中的内容为下标， { 0 , 1 , 2 , 3 , 4 } \{0,1,2,3,4\} {0,1,2,3,4} 分别表示 { A , B , C , D } \{A,B,C,D\} {A,B,C,D} ，$-1$ 表示空或前驱顶点为本身。

5. 完整代码

5.1 邻接矩阵

邻接矩阵的代码包括图的遍历和所有图的算法。

#include <vector>
#include <map>
#include <iostream>
#include <queue>
#include <iomanip>
using namespace std;

class UnionFindSet
{
public:
	UnionFindSet(size_t size) :_ufs(size, -1) {}

	int FindRoot(int index)
	{
		if (_ufs[index] < 0)
		{
			return index;
		}
		return _ufs[index] = FindRoot(_ufs[index]);
	}

	bool Union(int x, int y)
	{
		int root1 = FindRoot(x);
		int root2 = FindRoot(y);

		//如果两个元素本就在同一个集合返回false
		if (root1 == root2)
		{
			return false;
		}

		//按秩合并，将较矮的树合并到较高的树下
		//由于用负数表示秩，值越小树的高度越高
		if (_ufs[root1] > _ufs[root2])
			swap(root1, root2);

		// 将集合 root2 合并到 root1 上
		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
		return true;
	}

	int Count()
	{
		int count = 0;
		for (auto it : _ufs)
		{
			if (it < 0)
			{
				count++;
			}
		}
		return count;
	}

	bool InSet(int x, int y)
	{
		return FindRoot(x) == FindRoot(y);
	}

private:
	vector<int> _ufs;
};

//邻接矩阵
template<class V,class W,W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
	typedef Graph<V, W, MAX_W, Direction> Self;
	Graph() = default;
	Graph(const V* vertexs, size_t n)
	{
		_vertexs.reserve(n);
		for (size_t i = 0; i < n; i++)
		{
			_vertexs.push_back(vertexs[i]);
			_vIndexMap[vertexs[i]] = i;
		}
		//用MAX_W表示无穷大
		_matrix.resize(n, vector<W>(n, MAX_W));
	}

	size_t GetVertexIndex(const V& v)
	{
		auto ret = _vIndexMap.find(v);
		if (ret != _vIndexMap.end())
		{
			return ret->second;
		}
		else
		{
			throw invalid_argument("不存在的顶点");
			return -1;
		}
	}

	void AddEdge(const V& src, const V& dest, const W& w)
	{
		size_t srci = GetVertexIndex(src);
		size_t desti = GetVertexIndex(dest);
		_matrix[srci][desti] = w;
		if (Direction == false)
		{
			_matrix[desti][srci] = w;
		}
	}

	void PrintMatrix() const
	{
		cout << "邻接矩阵：" << endl;
		for (const auto& row : _matrix)
		{
			for (const auto& weight : row)
			{
				if (weight == MAX_W)
					cout << "∞\t";  // 用 "∞" 表示无穷大
				else
					cout << weight << "\t";
			}
			cout << endl;
		}
	}

	void BFS(const V& src)
	{
		size_t srcindex = GetVertexIndex(src);
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过

		queue<int> q;
		q.push(srcindex);
		isvisted[srcindex] = true;
		size_t d = 1;
		size_t dsize = 1;
		while (!q.empty())
		{
			dsize = q.size();
			cout << "Level"<<d<<": ";
			while (dsize--)
			{
				size_t front = q.front();
				q.pop();
				for (size_t i = 0; i < _vertexs.size(); i++)
				{
					if (isvisted[i] == false && _matrix[front][i] != MAX_W)
					{
						cout<< "["<<_vertexs[i] << ":" << _matrix[front][i]<<"]";
						isvisted[i] = true;
						q.push(i);
					}
				}
			}
			cout << endl;
			d++;
		}
	}

	void _DFS(const V& v, vector<bool>& isvisted)
	{
		cout << v << " ";
		int index = GetVertexIndex(v);
		for (int i = 0; i < _vertexs.size(); i++)
		{
			if (_matrix[index][i]!= MAX_W && !isvisted[i])
			{
				isvisted[i] = true;
				_DFS(_vertexs[i],isvisted);
			}
		}
	}

	void DFS(const V& v)
	{
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过
		int index = GetVertexIndex(v);
		isvisted[index] = true;
		_DFS(v, isvisted);
	}

	struct Edge
	{
		size_t _srci;
		size_t _desti;
		W _w;

		Edge(size_t srci,size_t desti,const W& w):_srci(srci),_desti(desti),_w(w){}

		bool operator>(const Edge& e) const
		{
			return _w > e._w;
		}
	};

	W Kruskal(Self& minTree)
	{
		minTree._vertexs = _vertexs;
		minTree._vIndexMap = _vIndexMap;
		minTree._matrix.resize(_vertexs.size());
		for (auto& it : minTree._matrix)
		{
			it.resize(_vertexs.size(), MAX_W);
		}

		priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (i < j && _matrix[i][j] != MAX_W)
				{
					minque.push(Edge(i, j, _matrix[i][j]));//minque的第一个元素总是权值最小的边
				}
			}
		}

		int size = 0;
		W totalW = W();
		UnionFindSet ufs(_vertexs.size());
		while (!minque.empty())
		{
			Edge min = minque.top();
			minque.pop();
			if (!ufs.InSet(min._srci, min._desti))
			{
				minTree.AddEdge(_vertexs[min._srci], _vertexs[min._desti], min._w);
				cout << _vertexs[min._srci] << "-" << min._w << ">" << _vertexs[min._desti] << endl;
				ufs.Union(min._srci, min._desti);
				size++;
				totalW += min._w;
			}
		}
		if (size == _vertexs.size() - 1)
		{
			//如果能够构建最小生成树
			return totalW;
		}
		else
		{
			return W();
		}
	}

	W Prim(Self& minTree,const V& src)
	{
		minTree._vertexs = _vertexs;
		minTree._vIndexMap = _vIndexMap;
		minTree._matrix.resize(_vertexs.size());
		for (auto& it : minTree._matrix)
		{
			it.resize(_vertexs.size(), MAX_W);
		}

		size_t srci = GetVertexIndex(src);

		//用X存储在生成树中的顶点，用Y存储不在生成树中的顶点
		vector<bool> inTree(_vertexs.size(), false);
		inTree[srci] = true;

		priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			if (_matrix[srci][i] != MAX_W)
			{
				minque.push(Edge(srci, i, _matrix[srci][i]));//先将根节点所有的边放入优先队列中
			}
		}
		size_t size = 0;
		W totalW = W();
		while (!minque.empty())
		{
			Edge min = minque.top();
			minque.pop();

			//如果最小边在X里，连接会构成环
			if (inTree[min._desti])
			{
				continue;
			}
			else
			{
				minTree.AddEdge(_vertexs[min._srci], _vertexs[min._desti], min._w);
				cout << _vertexs[min._srci] << "-" << min._w << ">" << _vertexs[min._desti] << endl;
				inTree[min._desti] = true;
				size++;
				totalW += min._w;

				if (size == _vertexs.size() - 1)
				{
					//如果最小生成树构建完，退出循环
					break;
				}
				for (size_t i = 0; i < _vertexs.size(); i++)
				{
					if (_matrix[min._desti][i] != MAX_W && !inTree[i])
					{
						//将新连接的顶点放入最小生成树中
						minque.push(Edge(min._desti, i, _matrix[min._desti][i]));
					}
				}
			}
		}
		if (size == _vertexs.size() - 1)
		{
			return totalW;
		}
		else
		{
			return W();
		}
	}

	void Dijstra(const V& src)
	{
		vector<int> dist(_vertexs.size(), MAX_W);
		vector<int> parentPath(_vertexs.size(), MAX_W);
		size_t srci = GetVertexIndex(src);

		vector<bool> confirm(_vertexs.size(), false);//存储已确定最短路径的顶点
		dist[srci] = W();//源点的最短路径是最小值

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			W min = MAX_W;	//最短路径，初值为最大值
			size_t u = srci;

			//遍历当前顶点的最小的边，更新符合条件的最短路径
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (confirm[j] == false && dist[j] < min)
				{
					min = dist[j];
					u = j;
				}
			}

			confirm[u] = true;	//顶点u的最短路径确定

			//遍历顶点 u 相邻的所有顶点，查找能够更新最短路径的顶点
			for (size_t k = 0; k < _vertexs.size(); k++)
			{
				//如果顶点k没有确定最短路径，且u和k相邻，且此时从源点到u的距离加上u到k的距离小于此时k的最短路径
				if (confirm[k] == false && _matrix[u][k] != MAX_W && dist[u] + _matrix[u][k]<dist[k])
				{
					cout << _vertexs[k] << "的最短路径由 " << dist[k] << " 更新为 " << dist[u] + _matrix[u][k] << endl;
					dist[k] = dist[u] + _matrix[u][k];
					parentPath[k] = u;
				}
			}
		}
	}

	bool BellmanFord(const V& src)
	{
		vector<int> dist(_vertexs.size(), MAX_W);
		vector<int> parentPath(_vertexs.size(), MAX_W);
		size_t srci = GetVertexIndex(src);
		dist[srci] = W();	//源点的最短路径为最小值

		for (size_t k = 0; k < _vertexs.size() - 1; k++)
		{
			bool exchange = false;//用于判断是否有最短路径发生更新
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
					{
						cout << _vertexs[j] << "的最短路径由 " << dist[j] << " 更新为 " << dist[i] + _matrix[i][j] << endl;
						//源点到i+i到j<源点到j，就更新最短路径
						dist[j] = dist[i] + _matrix[i][j];
						parentPath[j] = i;
						exchange = true;
					}
				}
			}
			if (exchange == false)
			{
				break;
			}
		}

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				//检查是否有负权回路
				if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					//最短路径求完，但有从源点到i+i到j<从源点到j，说明存在负权回路
					return false;
				}
			}
		}
		return true;
	}

	void FloydWarshall()
	{
		vector<vector<W>> vvDist(_vertexs.size(), vector<int>(_vertexs.size(), MAX_W));
		vector<vector<int>> vvParentPath(_vertexs.size(), vector<int>(_vertexs.size(), 0));

		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (_matrix[i][j] != MAX_W)
				{
					//初始化D(0)和P(0)矩阵的内容
					vvDist[i][j] = _matrix[i][j];
					vvParentPath[i][j] = i;
				}
				//这里用-1表示P矩阵中i到j没有路径或j就是i的情况
				else
				{
					//i到j没有路径
					vvParentPath[i][j] = -1;
				}
				if (i == j)
				{
					//j就是i
					vvDist[i][j] = 0;
					vvParentPath[i][j] = -1;
				}
			}
		}

		//打印矩阵变化过程
		std::cout << std::showpos;
		cout << "D(0):" << "           " << "P(0):" << endl;
		for (size_t i = 0; i < _vertexs.size(); i++)
		{
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				if (vvDist[i][j] == MAX_W)
				{
					cout<<" * ";
				}
				else
				{
					cout << vvDist[i][j] << " ";
				}
			}
			cout << "       ";
			for (size_t j = 0; j < _vertexs.size(); j++)
			{
				cout << vvParentPath[i][j] << " ";
			}
			cout << endl;
		}

		int n = 1;
		//k表示中间顶点
		for (size_t k = 0; k < _vertexs.size(); k++)
		{
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (vvDist[i][k] != MAX_W && vvDist[k][j]!=MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
					{
						//如果从i经过k到j的路径比当前从i到j的最短路径更短，就更新最短路径
						vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
						vvParentPath[i][j] = vvParentPath[k][j];
					}
				}
			}
			//打印矩阵变化过程
			cout << "====================================================" << endl;
			cout << "D(" << n << "):" << "           " << "P(" << n << "):" << endl;
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					if (vvDist[i][j] == MAX_W)
					{
						cout << " * ";
					}
					else
					{
						cout << vvDist[i][j] << " ";
					}

				}
				cout << "       ";
				for (size_t j = 0; j < _vertexs.size(); j++)
				{
					cout << vvParentPath[i][j] << " ";
				}
				cout << endl;
			}
			n++;
		}
	}

private:
	map<V, size_t> _vIndexMap;//快速查找顶点在邻接矩阵中的索引
	vector<V> _vertexs;		//顶点集合
	vector<vector<W>> _matrix;	//边的邻接矩阵
};

5.2 邻接表

邻接表的代码没有最短路径的代码。

#include <vector>
#include <map>
#include <iostream>
#include <string>
#include <queue>
using namespace std;

//邻接表
template<class W>
class LinkEdge
{
public:
	int _srcIndex;
	int _destIndex;
	W _w;
	LinkEdge<W>* _next;

	LinkEdge(const W& w):_srcIndex(-1),_destIndex(-1),_w(w),_next(nullptr)
	{}
};

template<class V, class W, bool Direction = false>
class Graph
{
public:
	typedef LinkEdge<W> Edge;
	Graph(const V* vertex,size_t n)
	{
		for (size_t i = 0; i < n; i++)
		{
			_vertexs.push_back(vertex[i]);
			_vIndexMap[vertex[i]] = i;
		}

		_tables.resize(n, nullptr);
	}

	size_t GetVertexIndex(const V& v)
	{
		auto ret = _vIndexMap.find(v);
		if (ret != _vIndexMap.end())
		{
			return ret->second;
		}
		else
		{
			throw invalid_argument("不存在的顶点");
			return -1;
		}
	}

	void AddEdge(const V& src, const V& dest, const W& w)
	{
		size_t srcIndex = GetVertexIndex(src);
		size_t destIndex = GetVertexIndex(dest);
		
		Edge* edge = new Edge(w);
		edge->_srcIndex = srcIndex;
		edge->_destIndex = destIndex;
		//头插
		edge->_next = _tables[srcIndex];
		_tables[srcIndex] = edge;

		if (Direction == false)
		{
			Edge* dest_edge = new Edge(w);
			dest_edge->_srcIndex = destIndex;
			dest_edge->_destIndex = srcIndex;
			dest_edge->_next = _tables[destIndex];
			_tables[destIndex] = dest_edge;
		}
	}

	void PrintGraph() const
	{
		for (size_t i = 0; i < _tables.size(); i++)
		{
			cout << _vertexs[i] << " -> ";
			Edge* p = _tables[i];
			while (p != nullptr)
			{
				cout << "[" << _vertexs[p->_destIndex] << ", " << p->_w << "] ";
				p = p->_next;
			}
			cout << endl;
		}
	}

	void _DFS(int index, vector<bool>& isvisted)
	{
		isvisted[index] = true;
		cout << _vertexs[index] << " ";
		Edge* edge = _tables[index];
		while (edge)
		{
			if (!isvisted[edge->_destIndex])
			{
				_DFS(edge->_destIndex, isvisted);
			}
			edge = edge->_next;
		}
	}

	void DFS(const V& v)
	{
		vector<bool> isvisted(_vertexs.size(), false);
		int index = GetVertexIndex(v);
		_DFS(index, isvisted);
	}

	void BFS(const V& v)
	{
		vector<bool> isvisted(_vertexs.size(), false);	//存储顶点是否已经被遍历过
		queue<int> q;
		int index = GetVertexIndex(v);
		q.push(index);
		isvisted[index] = true;
		while (!q.empty())
		{
			int currentIndex = q.front();
			q.pop();

			cout << _vertexs[currentIndex] << " ";
			Edge* edge = _tables[currentIndex];
			while (edge)
			{
				if (!isvisted[edge->_destIndex])
				{
					q.push(edge->_destIndex);
					isvisted[edge->_destIndex] = true;
				}
				edge = edge->_next;
			}
		}
	}
private:
	map<string, int> _vIndexMap;//快速查找顶点在邻接矩阵中的索引
	vector<V> _vertexs;		//顶点集合
	vector<Edge*> _tables;	//邻接表
};

5.3 测试用例

void TestBFS_and_DFS()
{

	string a[] = { "A", "B", "C", "D" ,"E","F","G","H" };
	Graph<string, int> g1(a, 8);
	g1.AddEdge("A", "B", 10);
	g1.AddEdge("A", "F", 20);
	g1.AddEdge("B", "C", 30);
	g1.AddEdge("C", "D", 40);
	g1.AddEdge("C", "E", 50);
	g1.AddEdge("D", "E", 60);
	g1.AddEdge("D", "G", 70);
	g1.AddEdge("G", "H", 80);
	g1.AddEdge("G", "F", 90);

	//g1.BFS("A");
	//g1.DFS("A");
}

void TestKruskal_and_Prim()
{
	string a[] = { "a", "b", "c", "d" ,"e","f","g","h","i"};
	Graph<string, int> g1(a, 9);
	g1.AddEdge("a", "b", 4);
	g1.AddEdge("b", "h", 11);
	g1.AddEdge("a", "h", 8);
	g1.AddEdge("b", "c", 8);
	g1.AddEdge("c", "d", 7);
	g1.AddEdge("c", "i", 2);
	g1.AddEdge("d", "e", 9);
	g1.AddEdge("d", "f", 14);
	g1.AddEdge("e", "f", 10);
	g1.AddEdge("f", "g", 2);
	g1.AddEdge("f", "c", 4);
	g1.AddEdge("g", "i", 6);
	g1.AddEdge("g", "h", 1);
	g1.AddEdge("h", "i", 7);

	Graph<string, int> minTree;
	g1.Kruskal(minTree);
	//cout<< g1.Prim(minTree,"a");
	//minTree.PrintMatrix();

}

void TestDijstra()
{
	const char* str = "syztx";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 10);
	g.AddEdge('s', 'y', 5);
	g.AddEdge('y', 't', 3);
	g.AddEdge('y', 'x', 9);
	g.AddEdge('y', 'z', 2);
	g.AddEdge('z', 's', 7);
	g.AddEdge('z', 'x', 6);
	g.AddEdge('t', 'y', 2);
	g.AddEdge('t', 'x', 1);
	g.AddEdge('x', 'z', 4);
	g.Dijstra('s');
}

void TestBellmanFord()
{
	const char* str = "syztx";
	Graph<char, int, INT_MAX, true> g(str, strlen(str));
	g.AddEdge('s', 't', 6);
	g.AddEdge('s', 'y', 7);
	g.AddEdge('y', 'z', 9);
	g.AddEdge('y', 'x', -3);
	g.AddEdge('z', 's', 2);
	g.AddEdge('z', 'x', 7);
	g.AddEdge('t', 'y', 8);
	g.AddEdge('t', 'x', 5);
	g.AddEdge('t', 'z', -4);
	g.AddEdge('x', 't', -2);
	g.BellmanFord('s');
}

void TestFloydWarshall()
{
	string a[] = { "A", "B", "C", "D" ,"E" };
	Graph<string, int, INT_MAX, true> g1(a, 5);
	g1.AddEdge("A", "B", 3);
	g1.AddEdge("A", "E", -4);
	g1.AddEdge("A", "C", 8);
	g1.AddEdge("B", "E", 7);
	g1.AddEdge("B", "D", 1);
	g1.AddEdge("C", "B", 4);
	g1.AddEdge("D", "C", -5);
	g1.AddEdge("D", "A", 2);
	g1.AddEdge("E", "D", 6);

	g1.FloydWarshall();
}