讲解视频：可以在bilibili搜索“MATLAB教程新手入门篇——数学建模清风主讲”。

MATLAB教程新手入门篇（数学建模清风主讲，适合零基础同学观看）_哔哩哔哩_bilibili

以下内容节选自第三章3.5节

norm函数

它可以用来计算向量或者矩阵的范数。范数这个概念大家可能没听过，它在机器学习中用的较多。

我们这里只介绍向量的范数，假设向量，常用的向量范数有下面三种：

1-范数： ,  即对x的元素求绝对值后再求和。

2-范数：, 即对x的元素求平方后再求和，然后再开方。

p-范数：, 即对x元素的绝对值求p次方，再求和，最后再算1/p次幂。

在MATLAB中的调用方法分别为：norm(x,1)、norm(x,2)和norm(x,p)。事实上，1-范数和2-范数都属于p-范数的特例，MATLAB中p默认取2，即norm(x)是norm(x,2)的简写形式，表示计算2-范数。

我们来看几个例子：

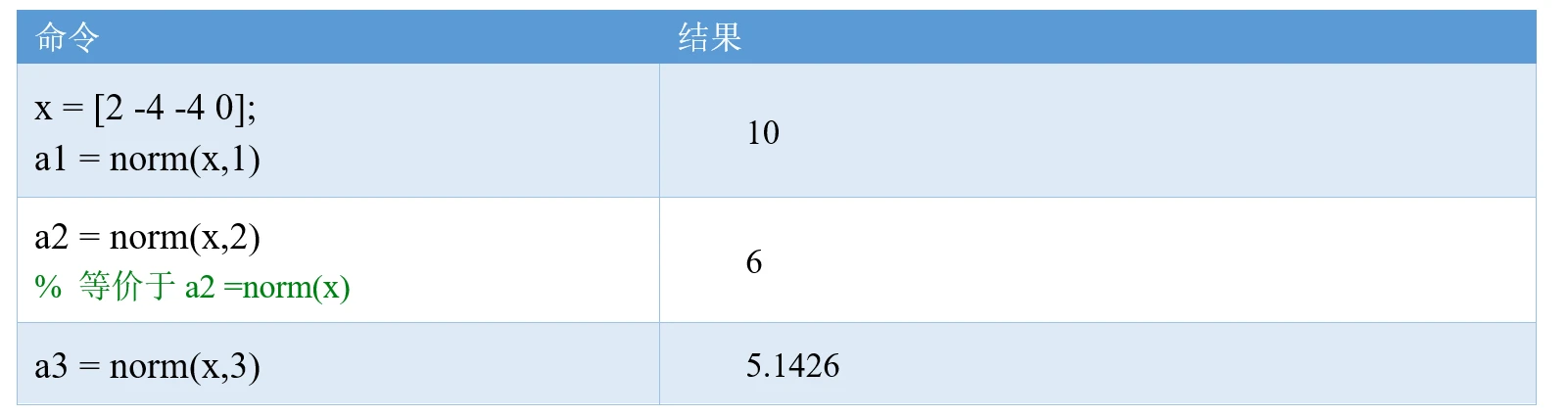
事实上，如果你不会norm函数，也可以用我们之前的方法计算向量的范数：p-范数等价于：sum(abs(x).^p) ^ (1/p)，这里的1/p要加括号。特别地，将p分别取1和2即可得到1-范数和2-范数。