1数据集

编号,密度,含糖率,好瓜
1,0.697,0.46,是
2,0.774,0.376,是
3,0.634,0.264,是
4,0.608,0.318,是
5,0.556,0.215,是
6,0.403,0.237,是
7,0.481,0.149,是
8,0.437,0.211,是
9,0.666,0.091,否
10,0.243,0.267,否
11,0.245,0.057,否
12,0.343,0.099,否
13,0.639,0.161,否
14,0.657,0.198,否
15,0.36,0.37,否
16,0.593,0.042,否
17,0.719,0.103,否

2模型代码

import csv
import numpy as np
from matplotlib import pyplot as plt
class logodds_regress(object):

    def sigmoid(self,z):
        '''
        @param z:beta * xi
        '''
        return 1/(1 + np.exp(-z))

    def lossfunc(self,y,z):
        '''
        @param y:标签
        @param z:beta * x_i
        @return:返回目标函数值
        '''
        return np.sum(-y*z + np.log(1+np.exp(z)))
        
    def dl_to_beta(self,xtrain,ytrain,beta):
        '''
        @param xtrain:(x,1) shape[N,d+1]
        @param ytrain:label shape[N,1]
        @param beta:  (w,b) shape [1,d+1]
        @return beta
        '''
        #shape [N, 1]
        z = np.dot(xtrain,beta.T)
        p1 = np.exp(z) / (1 + np.exp(z))
        #shape [N, N]
        p = np.diag((p1 * (1-p1)).reshape(-1))#生成对角阵
        #shape [N, 1]
        dl1 = -np.sum(xtrain * (ytrain - p1), 0, keepdims=True)     #按列相加，保持矩阵的二维性
        #shape [3, 3]
        dl2 = xtrain.T .dot(p).dot(xtrain)
        beta -= np.dot(dl1,np.linalg.inv(dl2))
        return beta

    def newton(self,xtrain, ytrain):
        '''
        牛顿迭代法求解beta
        @param xtrain:(x,1) shape[N,d+1]
        @param ytrain:label shape[N,1]
        @return beta (w,b) shape [1,d+1]
        '''
        #initialization
        beta = np.ones((1, 3))
        #shape [N, 1]
        z = np.dot(beta,xtrain.T)
        #log-likehood
        loss_current = 0
        loss_next = self.lossfunc(ytrain,z)
        err = 1e-5  
        while( np.abs(loss_current-loss_next) > err):
            beta = self.dl_to_beta(xtrain,ytrain,beta)
            z = np.dot(beta,xtrain.T)
            loss_current = loss_next
            loss_next = self.lossfunc(ytrain,z)
        return beta

    def gradient_descent(self,xtrain,ytrain):
        '''
        梯度下降法求解beta
        @param xtrain:(x,1) shape[N,d+1]
        @param ytrain:label shape[N,1]
        @return beta (w,b) shape [1,d+1]
        '''
        beta = np.ones((1,3)) * 0.1
        z = np.dot(xtrain,beta.T)
        learn_rate = 0.05
        iter_max = 2000
        for i in range(iter_max):
            p1 = np.exp(z) / (1 + np.exp(z))
            #shape [N, N]
            p = np.diag((p1 * (1-p1)).reshape(-1))#生成对角阵
            #shape [N, 1] 一阶导数
            dl1 = -np.sum(xtrain * (ytrain - p1), 0, keepdims=True) #按列相加，保持矩阵的二维性
            beta -= dl1 * learn_rate
            z = np.dot(xtrain,beta.T)
        return beta
    def solver_sklearn(self,xtrain,ytrain):
        '''
        sklearn 模块中的lbfgs方法求beta
        @param xtrain:(x,1) shape[N,d+1]
        @param ytrain:label shape[N,1]
        @return beta (w,b) shape [1,d+1]
        '''
        from sklearn.linear_model import LogisticRegression
        reg = LogisticRegression(solver='lbfgs', C=1000).fit(xtrain,ytrain)
        beta = np.c_[reg.coef_,reg.intercept_]
        return beta 

    def model(self,xtrain,ytrain,solver='newton'):

        if solver == 'newton':
            return self.newton(xtrain,ytrain)
        elif solver == 'gradient_descent':
            return self.gradient_descent(xtrain,ytrain)
        elif solver == 'solver_sklearn':
            xtrain = np.delete(xtrain,-1,axis=1)
            return self.solver_sklearn(xtrain,ytrain)
        else:
            raise ValueError('Unknown method {}'.format(solver))

    def predict(self,beta,xtest):
        '''
        #我们以0.5为界，预测值y大于0.5则判断为好瓜，赋值1；反之判断为不是好瓜，赋值0 
        '''
        z = beta.dot(xtest.T)
        ypredict = self.sigmoid(z)
        ypredict[ypredict>0.5] = 1
        ypredict[ypredict<=0.5] = 0
        ypredict = ypredict.reshape(-1,1)
        return ypredict

def read_waremelon_data(filename):
    '''
    读取西瓜数据并转换
    @param filename:数据文件
    '''
    with open(filename,newline='',encoding='utf-8') as csvfile:
        data = csv.DictReader(csvfile)
        judge_to_num = {'是':1,'否':0}
        density = []     #密度
        sugar_rate = []  #含糖率
        y = []           #标签
        for item in data:
            density.append(float(item['密度']))
            sugar_rate.append(float(item['含糖率']))
            y.append(judge_to_num[item['好瓜']])
    density = np.array(density)
    sugar_rate = np.array(sugar_rate)
    xtrain = np.hstack((density.reshape(-1,1),sugar_rate.reshape(-1,1)))
    return (xtrain,y)
    

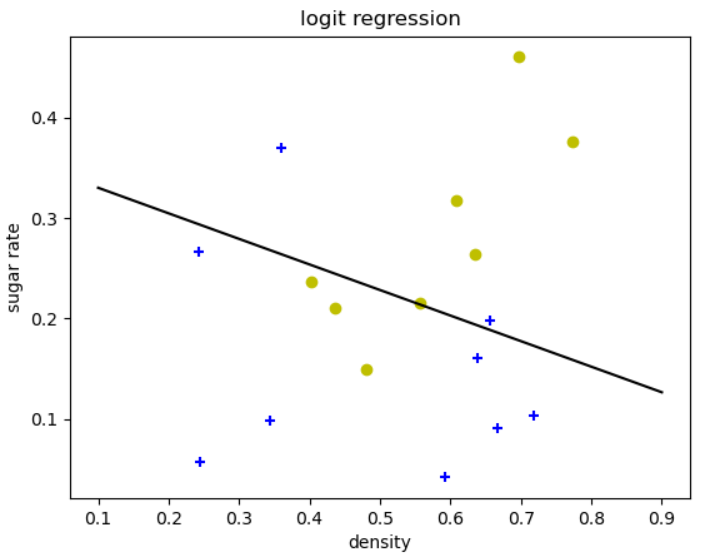
if __name__=='__main__':
    filename = 'table45.csv'
    xtrain,y = read_waremelon_data(filename)
    ###绘制训练数据
    y=np.array(y)
    data_label1 = xtrain[y==1,:]
    data_label0 = xtrain[y==0,:]
    plt.scatter(data_label1[:, 0], data_label1[:, 1], c='y', marker='o')
    plt.scatter(data_label0[:, 0], data_label0[:, 1], c='b', marker='+')
  
    ###数据w->beta,x->\hat{x}
    #shape [N,3]
    xtrain = np.hstack((xtrain,np.ones([len(y),1])))
    #shape [N,1]
    ytrain = y.reshape(-1,1)
    ### 建模
    A = logodds_regress()
    beta = A.model(xtrain,ytrain,solver='solver_sklearn')
    ypredict = A.predict(beta,xtrain)
    print(ypredict)
    print('准确率',sum(ytrain==ypredict)/len(ytrain))
    ###绘图直线方程w1x1+w2x2+b=0-->x2=-(w1x1+b)/w2
    ymin = -( beta[0, 0]*0.1 + beta[0, 2] ) / beta[0, 1]
    ymax = -( beta[0, 0]*0.9 + beta[0, 2] ) / beta[0, 1]
    plt.plot([0.1, 0.9], [ymin, ymax], 'k-')
    plt.xlabel('density')
    plt.ylabel('sugar rate')
    plt.title("logit regression")
    plt.show()

3预测结果