A星算法融合DWA算法实现规避未知障碍物的Matlab代码（全局规划算法融合动态窗口算法DWA） A星算法和DWA算法是两种常见的路径规划算法，其中A星算法主要用于静态环境下的最优路径规划，而DWA算法则更适用于动态环境下的路径规划。 为了解决实际场景中的路径规划问题，可以将这两种算法进行融合，达到更高效、准确的路径规划结果。 例如，在机器人路径规划中，可以利用A星算法计算出路线的大致方向，再用DWA算法对路线进行调整，以应对实时变化的环境因素。 通过算法融合，可以在满足最优性、实时性、安全性等多重条件下，实现机器人或其他智能设备的智能路径规划。

在机器人和智能设备的路径规划领域，A星算法和DWA算法可谓是两颗璀璨的“明星”。A星算法擅长在静态环境里寻找最优路径，而DWA算法则在动态环境中大展身手。将它们融合，能碰撞出怎样的火花呢？今天咱就一起来瞧瞧用Matlab实现A星算法融合DWA算法规避未知障碍物的奇妙之旅。

A星算法与DWA算法的“独门绝技”

A星算法，作为静态环境路径规划的佼佼者，它结合了Dijkstra算法的广度优先搜索和最佳优先搜索的优点。它通过一个评估函数$f(n)=g(n)+h(n)$来寻找路径，其中$g(n)$是从起点到节点$n$的实际代价，$h(n)$是从节点$n$到目标点的估计代价。这个评估函数帮助A星算法能更有针对性地搜索，快速找到最优路径。

% A星算法简单示意代码
function [path, cost] = astar(map, start, goal)
    % 初始化
    openSet = [start];
    cameFrom = containers.Map('KeyType', 'double', 'ValueType', 'double');
    gScore = containers.Map('KeyType', 'double', 'ValueType', 'double');
    fScore = containers.Map('KeyType', 'double', 'ValueType', 'double');
    gScore(start(1), start(2)) = 0;
    fScore(start(1), start(2)) = heuristic(start, goal);

    while ~isempty(openSet)
        % 找到fScore最小的节点
        [~, currentIndex] = min([fScore.values{:}]);
        current = openSet(currentIndex);
        openSet(currentIndex) = [];

        if isequal(current, goal)
            % 找到路径，回溯
            path = reconstructPath(cameFrom, current);
            cost = gScore(current(1), current(2));
            return;
        end

        % 遍历邻居节点
        neighbors = getNeighbors(current, map);
        for i = 1:size(neighbors, 1)
            neighbor = neighbors(i, :);
            tentativeGScore = gScore(current(1), current(2)) + 1;

            if ~gScore.isKey(neighbor(1), neighbor(2)) || tentativeGScore < gScore(neighbor(1), neighbor(2))
                cameFrom(neighbor(1), neighbor(2)) = current;
                gScore(neighbor(1), neighbor(2)) = tentativeGScore;
                fScore(neighbor(1), neighbor(2)) = tentativeGScore + heuristic(neighbor, goal);
                if ~ismember(neighbor, openSet, 'rows')
                    openSet = [openSet; neighbor];
                end
            end
        end
    end
    path = [];
    cost = Inf;
end

function h = heuristic(node, goal)
    h = abs(node(1) - goal(1)) + abs(node(2) - goal(2));
end

function neighbors = getNeighbors(node, map)
    neighbors = [];
    for dx = -1:1
        for dy = -1:1
            if dx == 0 && dy == 0
                continue;
            end
            neighbor = node + [dx, dy];
            if neighbor(1) >= 1 && neighbor(1) <= size(map, 1) && neighbor(2) >= 1 && neighbor(2) <= size(map, 2) && map(neighbor(1), neighbor(2)) == 0
                neighbors = [neighbors; neighbor];
            end
        end
    end
end

function path = reconstructPath(cameFrom, current)
    path = [current];
    while cameFrom.isKey(current(1), current(2))
        current = cameFrom(current(1), current(2));
        path = [current; path];
    end
end

上述代码简单实现了A星算法的核心逻辑。首先初始化一些数据结构，如开放集openSet，用于记录待探索的节点；cameFrom记录每个节点的前驱节点，方便最后回溯路径；gScore记录从起点到每个节点的实际代价；fScore记录评估函数值。在主循环中，不断从开放集里选取fScore最小的节点进行扩展，检查是否到达目标节点，若到达则回溯路径。同时计算邻居节点的gScore和fScore，决定是否将邻居节点加入开放集。

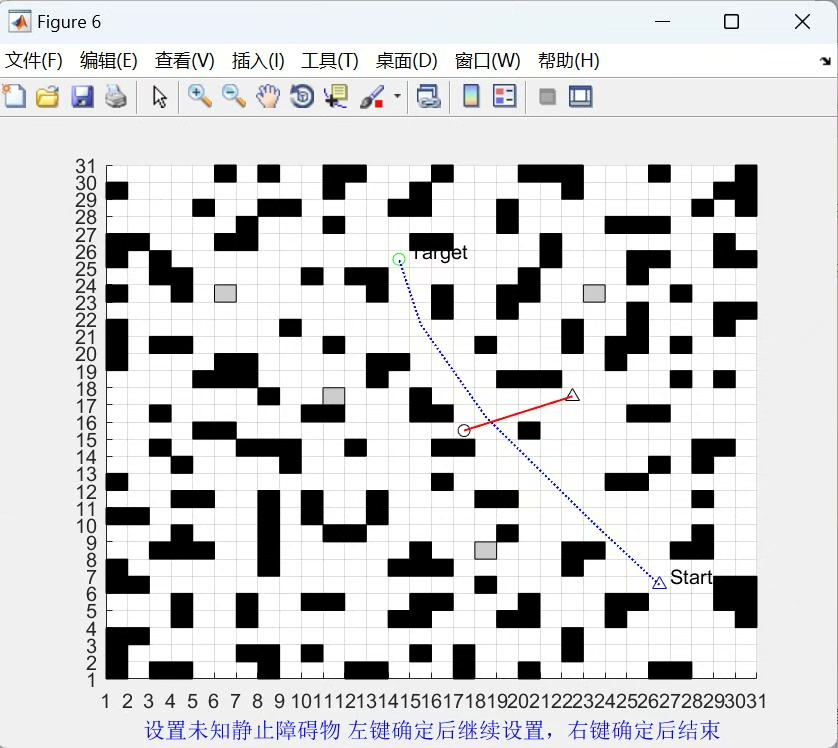
A星算法融合DWA算法实现规避未知障碍物的Matlab代码（全局规划算法融合动态窗口算法DWA） A星算法和DWA算法是两种常见的路径规划算法，其中A星算法主要用于静态环境下的最优路径规划，而DWA算法则更适用于动态环境下的路径规划。 为了解决实际场景中的路径规划问题，可以将这两种算法进行融合，达到更高效、准确的路径规划结果。 例如，在机器人路径规划中，可以利用A星算法计算出路线的大致方向，再用DWA算法对路线进行调整，以应对实时变化的环境因素。 通过算法融合，可以在满足最优性、实时性、安全性等多重条件下，实现机器人或其他智能设备的智能路径规划。

而DWA算法，主要考虑机器人当前的速度和加速度限制，在每个采样时刻，在机器人的动态可行速度集合中，根据优化目标函数选择一个最优的速度，使机器人朝着目标前进，同时避开障碍物。

融合两者，优势互补

在实际的机器人路径规划场景中，先利用A星算法计算出路线的大致方向，就像是给机器人绘制了一张“宏观地图”，让它知道大致该往哪走。然后，DWA算法闪亮登场，根据实时变化的环境因素，比如突然出现的障碍物，对路线进行精细调整。

Matlab代码实现融合

% 假设已经有A星算法和DWA算法的实现函数
% A星算法函数 astar(map, start, goal)
% DWA算法函数 dwa(robotState, map, goal, constraints)

% 初始化地图、起点和目标点
map = zeros(100, 100); % 简单的100x100地图，0表示可通行，1表示障碍物
map(20:30, 20:30) = 1; % 设置一些障碍物
start = [1, 1];
goal = [90, 90];

% 用A星算法获取大致路径
[astarPath, ~] = astar(map, start, goal);

% 假设机器人初始状态
robotState = [start(1), start(2), 0]; % [x, y, theta]
constraints.linear_velocity = [0, 1]; % 线速度范围
constraints.angular_velocity = [-pi/2, pi/2]; % 角速度范围

% 用DWA算法沿着A星路径调整
for i = 2:size(astarPath, 1)
    subGoal = astarPath(i, :);
    [newState, ~] = dwa(robotState, map, subGoal, constraints);
    % 更新机器人状态
    robotState = newState;
    % 这里可以添加绘图等可视化代码，展示路径调整过程
end

上述代码先初始化了一个简单的地图，设置了起点和目标点，调用A星算法获取大致路径。然后，假设机器人的初始状态和速度、角速度限制，通过循环，将A星算法获取路径上的点作为DWA算法的子目标，让DWA算法对路径进行实时调整，以应对动态环境。

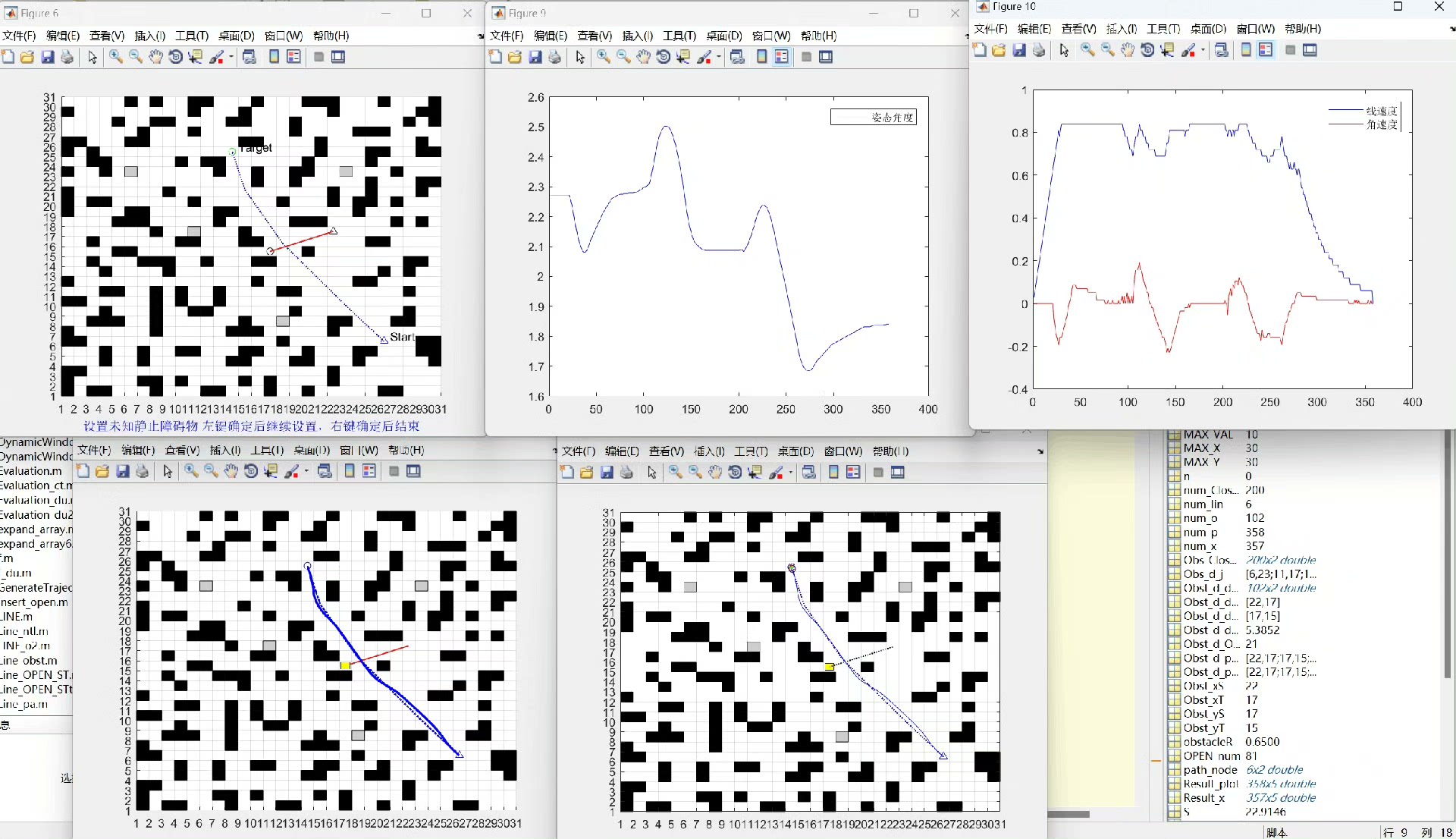
通过这样的算法融合，机器人在路径规划时能满足最优性、实时性和安全性等多重条件，在复杂多变的现实场景中也能游刃有余地找到合适路径。这就像是给机器人配备了一个既有宏观战略眼光，又能灵活应对突发状况的“智能大脑”。希望这篇博文能让大家对A星算法融合DWA算法在路径规划中的应用有更深入的理解，赶紧动手实践起来吧！