六自由度机械臂RRT路径规划算法梯形速度规划规划，实现机械臂避障。 并绘制相关曲线： 1.经过rrt算法规划得到的路径； 2.关节角度变化曲线、关节速度曲线； 3.机械臂避障动图。 代码有详细注释，自己学习后进行了标注和改进即可

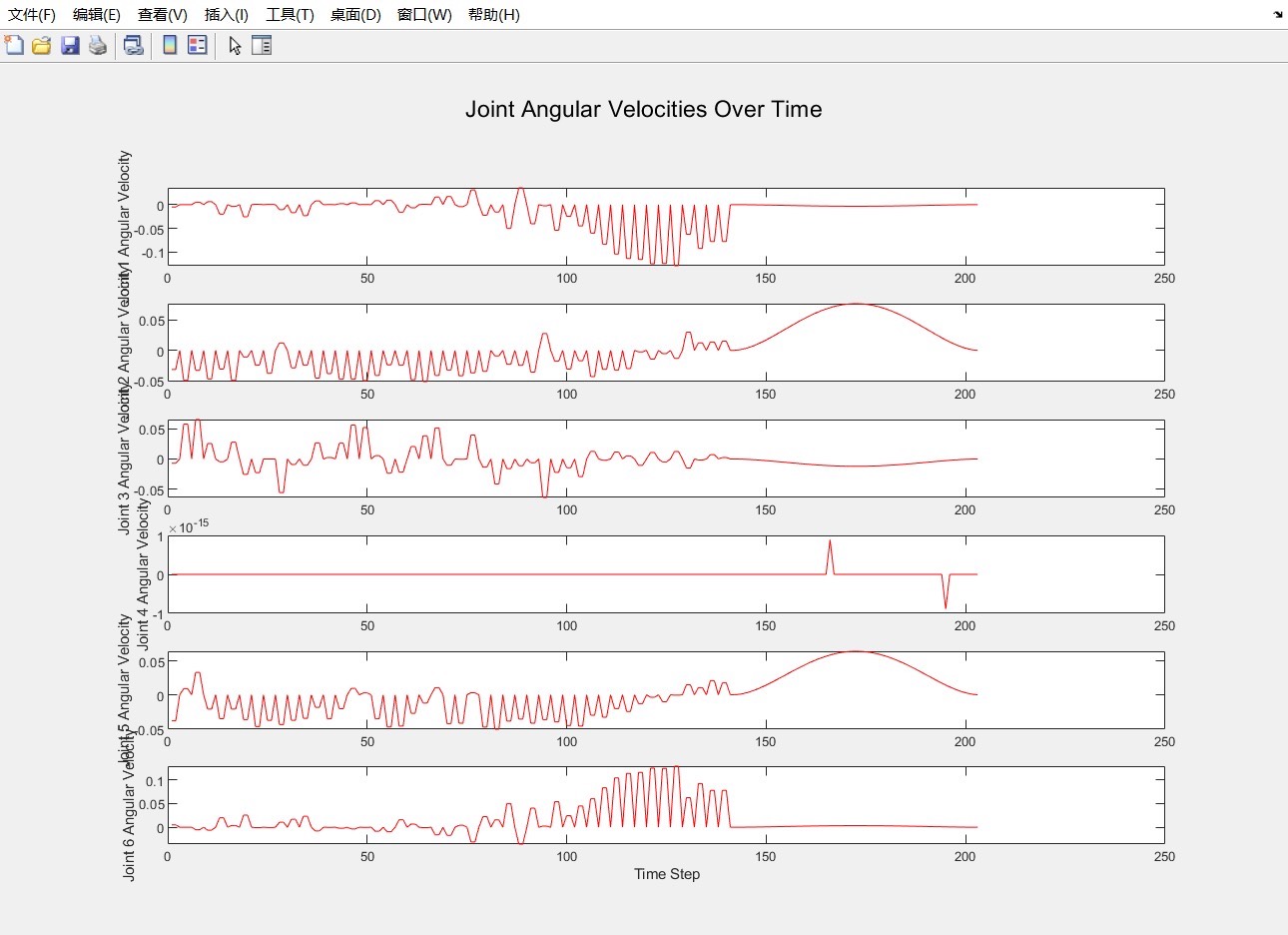
在机器人运动控制领域，六自由度机械臂的路径规划与避障是关键问题。本文将探讨如何使用RRT（快速探索随机树）算法进行路径规划，并结合梯形速度规划实现机械臂避障，同时绘制相关曲线辅助分析。

RRT路径规划算法原理

RRT算法是一种基于采样的路径搜索算法，通过在状态空间中随机采样点，并将新采样点连接到树中最近的节点，逐步构建一棵搜索树，直到找到目标节点或满足一定条件。

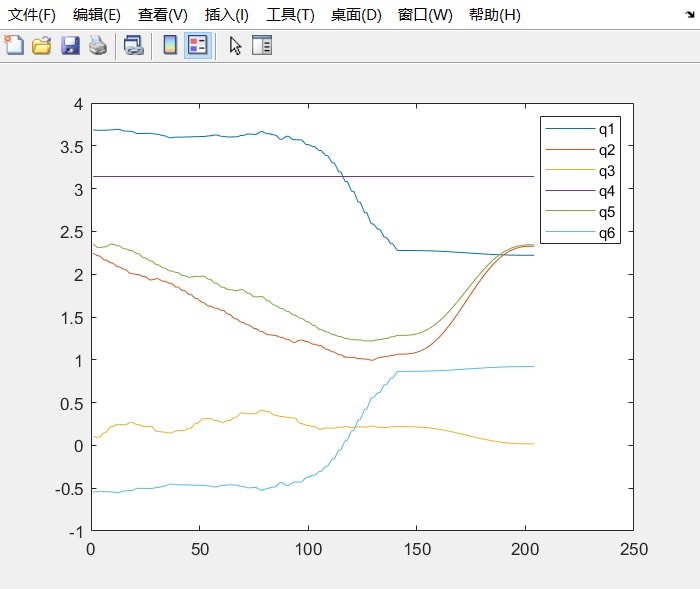
六自由度机械臂RRT路径规划算法梯形速度规划规划，实现机械臂避障。 并绘制相关曲线： 1.经过rrt算法规划得到的路径； 2.关节角度变化曲线、关节速度曲线； 3.机械臂避障动图。 代码有详细注释，自己学习后进行了标注和改进即可

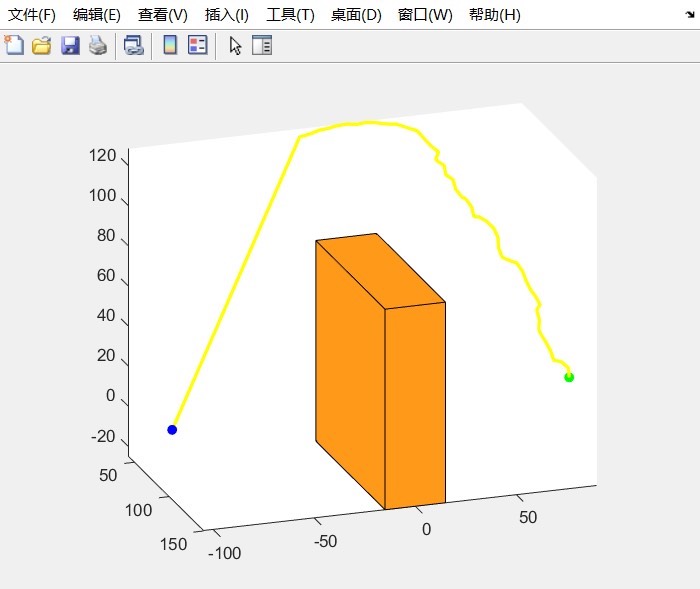
以下是简化的RRT算法Python代码示例（假设使用Python和numpy库）：

import numpy as np
import random


# 定义节点类
class Node:
    def __init__(self, position):
        self.position = position
        self.parent = None


# RRT算法主函数
def rrt(start, goal, obstacle_list, max_iter=1000):
    tree = []
    start_node = Node(start)
    tree.append(start_node)

    for i in range(max_iter):
        # 随机采样
        rand = np.array([random.uniform(-1, 1), random.uniform(-1, 1)])
        nearest_node = min(tree, key=lambda node: np.linalg.norm(node.position - rand))
        new_node = Node(nearest_node.position + (rand - nearest_node.position) * 0.1)

        # 检查是否与障碍物碰撞
        collision = False
        for obs in obstacle_list:
            if np.linalg.norm(new_node.position - obs) < 0.1:
                collision = True
                break

        if not collision:
            new_node.parent = nearest_node
            tree.append(new_node)

            # 检查是否接近目标
            if np.linalg.norm(new_node.position - goal) < 0.1:
                path = []
                current = new_node
                while current is not None:
                    path.append(current.position)
                    current = current.parent
                return path[::-1]

    return None

代码分析

1. Node类：用于表示树中的节点，每个节点包含自身位置和父节点信息。
2. rrt函数：主函数实现RRT算法。start和goal分别是起始点和目标点，obstaclelist是障碍物列表。在每次迭代中，随机采样一个点rand，找到树中距离rand最近的节点nearestnode，并根据一定步长生成新节点newnode。然后检查newnode是否与障碍物碰撞，如果没有碰撞则将其加入树中，并检查是否接近目标。若接近目标，则通过回溯父节点得到路径。

梯形速度规划

梯形速度规划用于控制机械臂在运动过程中的速度变化，以实现平稳加速、匀速和减速。

# 梯形速度规划函数
def trapezoidal_profile(v_max, a, s):
    # 计算加速阶段时间
    t_acc = v_max / a
    # 计算加速阶段位移
    s_acc = 0.5 * a * t_acc * t_acc
    # 计算匀速阶段位移
    s_const = s - 2 * s_acc
    # 计算匀速阶段时间
    t_const = s_const / v_max if s_const > 0 else 0
    # 计算总时间
    t_total = 2 * t_acc + t_const
    return t_acc, t_const, t_total

代码分析

1. trapezoidalprofile函数：输入最大速度vmax、加速度a和总位移s。首先计算加速阶段时间tacc和位移sacc，然后根据总位移计算匀速阶段位移sconst和时间tconst，最后得到总运动时间t_total。

实现机械臂避障及曲线绘制

结合上述算法，实现机械臂避障并绘制相关曲线。这里假设使用matplotlib绘制曲线，PIL库制作动图（实际应用中机械臂模型和动图绘制可能更复杂）。

import matplotlib.pyplot as plt
from PIL import Image, ImageDraw


# 假设这里有机械臂正逆运动学函数
def forward_kinematics(joint_angles):
    # 简单模拟，实际需根据机械臂结构实现
    return np.array([np.cos(joint_angles[0]), np.sin(joint_angles[0])])


def inverse_kinematics(position):
    # 简单模拟，实际需根据机械臂结构实现
    angle = np.arctan2(position[1], position[0])
    return np.array([angle])


# 示例使用
start = np.array([0, 0])
goal = np.array([0.8, 0.8])
obstacle_list = [np.array([0.5, 0.5])]

# RRT路径规划
path = rrt(start, goal, obstacle_list)

# 假设机械臂关节角度根据路径通过逆运动学计算得到
joint_angles = []
for pos in path:
    joint_angles.append(inverse_kinematics(pos))
joint_angles = np.array(joint_angles).flatten()

# 假设这里计算关节速度，简单模拟
joint_velocities = np.gradient(joint_angles)

# 绘制RRT路径
plt.figure()
plt.plot([p[0] for p in path], [p[1] for p in path], '-o')
for obs in obstacle_list:
    plt.plot(obs[0], obs[1], 'ro')
plt.title('RRT Path')
plt.xlabel('X')
plt.ylabel('Y')

# 绘制关节角度变化曲线
plt.figure()
plt.plot(joint_angles)
plt.title('Joint Angles')
plt.xlabel('Time Step')
plt.ylabel('Angle (rad)')

# 绘制关节速度变化曲线
plt.figure()
plt.plot(joint_velocities)
plt.title('Joint Velocities')
plt.xlabel('Time Step')
plt.ylabel('Velocity (rad/s)')

# 制作机械臂避障动图（简单模拟）
images = []
for i in range(len(path)):
    img = Image.new('RGB', (400, 400), (255, 255, 255))
    draw = ImageDraw.Draw(img)
    for obs in obstacle_list:
        draw.ellipse((obs[0] * 200 - 10, obs[1] * 200 - 10, obs[0] * 200 + 10, obs[1] * 200 + 10), fill='red')
    end_point = (path[i][0] * 200, path[i][1] * 200)
    draw.line((200, 200, end_point[0], end_point[1]), fill='blue', width=2)
    images.append(img)

images[0].save('obstacle_avoidance.gif', save_all=True, append_images=images[1:], duration=200, loop=0)

代码分析

1. 运动学函数模拟：forwardkinematics和inversekinematics函数是简单模拟，实际需根据机械臂结构精确实现。
2. 路径与关节角度计算：通过RRT算法得到路径后，假设使用逆运动学计算每个路径点对应的关节角度，并计算关节速度。
3. 曲线绘制：使用matplotlib分别绘制RRT路径、关节角度变化曲线和关节速度变化曲线。
4. 动图制作：使用PIL库简单模拟制作机械臂避障动图，在每个时间步绘制机械臂位置和障碍物。

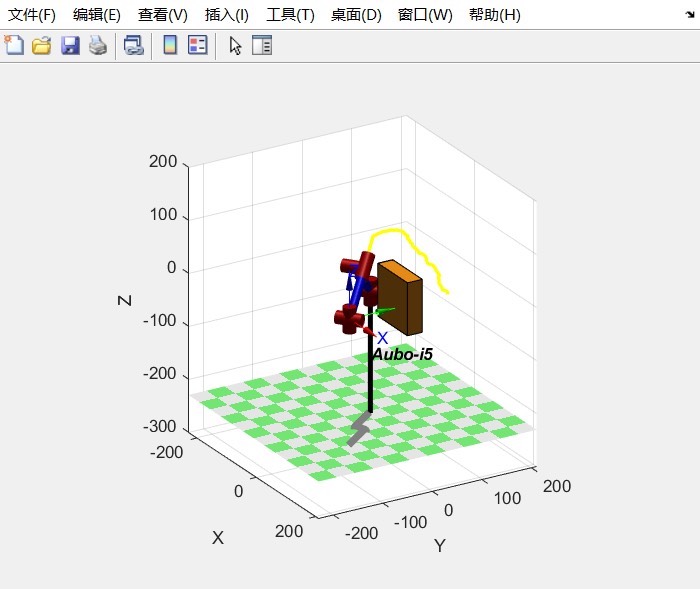
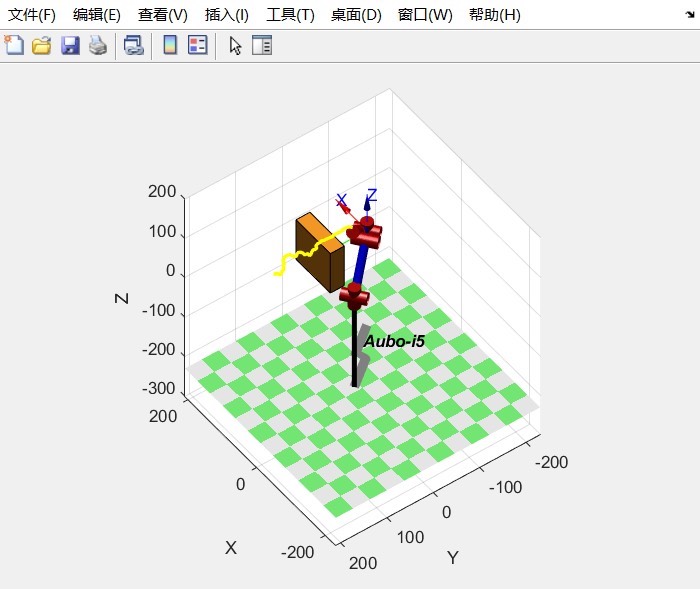
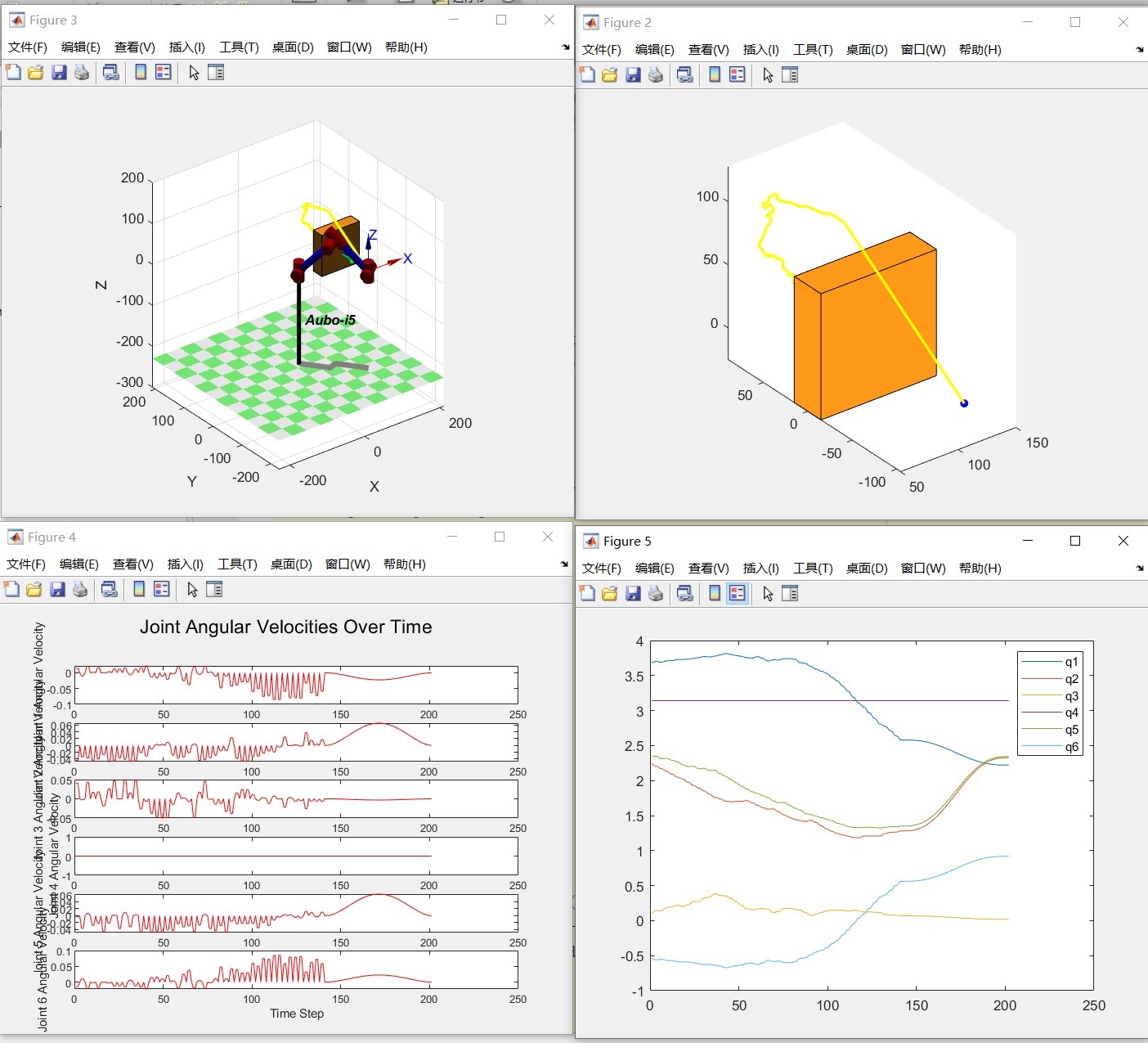
通过以上步骤，我们实现了六自由度机械臂的RRT路径规划与梯形速度规划避障，并绘制了相关曲线和动图辅助理解。实际应用中，还需根据具体机械臂结构和控制需求进行进一步优化和调整。