轮转数组

189. 轮转数组 - 力扣（LeetCode）

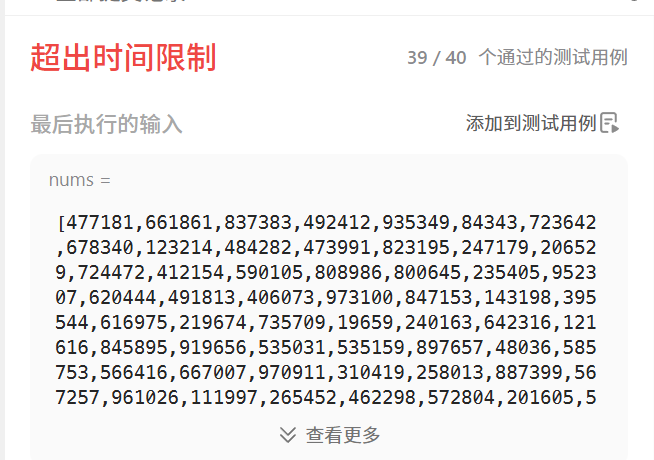
题目如下图所示：

思路1：暴力解法

暴力求解，用两个循环直接得出结果

时间复杂度O((n-1)*(n-1))==O(n)

for(int j=k;j>0;j--)
{
    int t = nums[numsSize-1];
    for(int i = numsSize-1;i>0;i--)
    {
        nums[i] = nums[i-1];
    }
    nums[0] = t;
}

缺点：时间复杂度高，易超出时间限制

思路2：三次翻转法

使用三次逆转法，让数组旋转k次
1. 先整体逆转
2. 逆转子数组[0, k - 1]
3. 逆转子数组[k, size - 1]

void reverse(int* nums, int begin, int end)
{
    while(begin < end)
    {
        int tmp = nums[begin];
        nums[begin] = nums[end];
        nums[end] = tmp;

        ++begin;
        --end;
    }
}

// 三趟逆置倒的思路
void rotate(int* nums, int numsSize, int k){
    if(k > numsSize)
    {
        k %= numsSize;
    }
    
    reverse(nums, 0, numsSize-1);
    reverse(nums, 0, k-1);
    reverse(nums, k, numsSize-1);
}

思路3：使用额外数组存储旋转后的结果

再用一个数组保存需要轮转的元素

问题1：能不能用int arr[]={0};来表示这个数组？

不能，它实际上创建了一个只包含一个元素的数组。

问题2：为什么可以用int nums1[m];

你可以在代码中使用 int nums1[m];，是因为你的编译器支持 C99 标准（或更新版本），这个标准引入了一个叫做变长数组 的特性。

1. 在 C++ 中：绝对不支持

VLA (变长数组) 从来都不是 C++ 标准的一部分。

2.在 C 语言中：基本不支持

这才是问题的核心。我的 LeetCode 代码是 .c 文件，所以讨论的是 C 语言。

• 历史原因：微软的 MSVC 编译器（VS 使用的编译器）在历史上对 C 语言标准的跟进一直比较缓慢。它长期停留在对 C89/C90 标准的完整支持上，而 VLA 是 C99 标准引入的特性。
• C11 标准的“退步”：C11 标准做了一个有趣的改动：它将 VLA 从一个“必须实现”的特性降级为了一个“可选实现”的特性。这意味着一个编译器可以声称自己是“C11 兼容”的，但可以不提供 VLA 功能。微软正是利用了这一点，选择不在 MSVC 中实现 VLA。

代码在 LeetCode 上能运行，是因为它的后台编译器（GCC）支持 C99 VLA。

void rotate(int* nums, int numsSize, int k) {
    k = k % numsSize;
    if(k == 0)
    {
        return;
    }
    if (k < numsSize) {
        int m = numsSize - k;
        int nums1[m];
        int nums2[k];
        for (int i = 0; i < m; i++) {
            nums1[i] = nums[i];
        }
        for (int i = 0; i < k; i++) // 01
        {
            nums2[i] = nums[m + i];
        }
        // 存入后面的
        for (int i = k; i < numsSize; i++) {
            nums[i] = nums1[i - k];
        }
        for (int i = 0; i < k; i++) {
            nums[i] = nums2[i];
        }
    }
}

返回倒数第K个节点

面试题 02.02. 返回倒数第 k 个节点 - 力扣（LeetCode）

题目如下图所示：

思路1：数组存储

将链表中的值存储到一个数组中

struct ListNode* cur = head;
    int length=0;
    while(cur)
    {
        length++;
        cur = cur->next;
    }
    int arr[length];//这里也是边长数组的使用
    struct ListNode* pcur = head;
    for(int i = 0;i < length;i++)
    {
        arr[i] = pcur->val;
        pcur = pcur->next;
    }
    return arr[length-k];

缺点：空间复杂度为O(n)，若题干限制为空间复杂度为O(1),则不能使用该思路

思路2：两次遍历

遍历两遍，第一遍确定链表个数，第二遍找到该节点

struct ListNode* cur = head;
    int length=0;
    while(cur)
    {
        length++;
        cur = cur->next;
    }
    struct ListNode* pcur = head;
    int m = length-k;//这里可以画图理解一下
    while(m)
    {
        pcur = pcur->next;
        m--;
    }
    return pcur->val;

缺点：若限制为一遍，则不成立

思路3：快慢指针

使用快慢指针的方法，快慢指针同时走，相差K个节点

int kthToLast(struct ListNode* head, int k) {
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    for(int i = 0;i < k;i++)
    {
        fast = fast->next;
    }
    while (fast) {
        slow = slow->next;
        fast = fast->next;
        
    }
    return slow->val;
}

总结

本文通过 轮转数组 和 返回倒数第k个节点 两道经典题目，深入分析了数组与链表操作中的不同解法效率：

轮转数组解法对比

思路	方法	时间复杂度	空间复杂度	优缺点
思路1	暴力移位法	O(k×n)	O(1)	实现简单，但k较大时会超时
思路2	三次翻转法	O(n)	O(1)	最优解，原地操作，效率高
思路3	额外数组法	O(n)	O(n)	思路直观，但空间占用大

返回倒数第k个节点解法对比

思路	方法	时间复杂度	空间复杂度	优缺点
思路1	数组存储法	O(n)	O(n)	简单直观，但空间复杂度高
思路2	两次遍历法	O(n)	O(1)	空间效率高，但需两次遍历
思路3	快慢指针法	O(n)	O(1)	最优解，只需一次遍历

可以看出，同一个问题，不同的算法设计会带来完全不同的效率表现。掌握复杂度分析，能帮助我们在实际开发中选择最合适的解法。

✅ 核心收获

• 数组旋转的三次翻转法：先整体逆序，再局部逆序，是一种巧妙的原地算法

• 链表的快慢指针思想：固定距离同步移动，一次遍历解决倒数第k个问题

• 取模运算：k = k % numsSize 是处理循环移位问题的关键

• VLA（变长数组）的使用：了解不同编译器的支持情况，写出兼容性更好的代码

• 空间换时间 vs 时间换空间：根据实际场景选择合适的策略

---

📌 下期预告

下一期我们将继续 【数据结构系列03】，进入链表进阶专题，一起来看看两道经典题目：

1. 【两个链表的第一个公共结点】：如何高效找到两个链表的交点？（面试高频题）

2. 【链表的回文结构】：如何判断一个链表是否为回文结构？（综合考查链表操作）

如果你对数组旋转或链表操作还有疑问，欢迎在评论区留言讨论！如果觉得有帮助，别忘了点赞、收藏、关注，我们下期见！

---

💡 小贴士：算法学习不是一蹴而就，建议你动手把本文的三种思路代码都跑一遍，感受不同算法在时间和空间上的差异。特别是快慢指针法，它是解决链表问题的利器，务必熟练掌握！