专栏目录

[1]URDF初析

---

前言

上一章写到UEDF基本语法，接下来黑马程序员讲了一些基础数学知识。以下仅个人看法，望请批评指正。数学知识板块分为运动学正解、运动学逆解两个部分，涉及知识点包括矩阵运算、三角函数、微积分。个人认为只能说有个大体框架，具体细节还需要经由学习、练习、考试、运用，诸多阶段。故而该部分为浅析框架，以示自明。

---

一、FK（运动学正解）

解释：简单来说，就是建立从关节空间到任务空间的映射。实际例子即为：给定一组已知的关节角度，求解机器人末端执行器在任务空间中的确切位姿。
解法分为：（1）齐次变换矩阵法 （2）解析几何与三角函数法 以下重点关注齐次变换矩阵法，解析几何与三角函数法在后续有更深入的理解再增加。

1.齐次变换矩阵法

1.1 齐次旋转矩阵：

(1)2D 齐次旋转矩阵

绕原点逆时针旋转 θ，齐次坐标
$$R_{2D}(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$
变换方程为：
$$\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
解得：
$$\begin{array}{rl}{x}^{\prime }& =x\cos \theta -y\sin \theta \\ y^{\prime }& =x\sin \theta +y\cos \theta \end{array}$$

其中,第一行表示移动后的x坐标，第二行表示移动后的y坐标，第三行为固定。

(1)3D 齐次旋转矩阵

然而，机器人的运动空间为三维，为此，黑马给出的解释是，将坐标系投影到各个面，再运用二维齐次旋转矩阵，即可求解。
我通过询问AI，它给出了3D 齐次旋转矩阵，仅做记录，有更深的理解了再做勘误解释：

1. 绕 x 轴旋转 θ
   $$R_x(\theta )=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$
2. 绕 y 轴旋转 θ
   $$R_y(\theta )=\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$
3. 绕 z 轴旋转 θ
   $$R_z(\theta )=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

1.2 齐次平移矩阵：

$$\left[\begin{array}{ccc}1& 0& tx\\ 0& 1& ty\\ 0& 0& 1\end{array}\right]$$
则最终，一个2D位移即可表示为：
$$\left[\begin{array}{ccc}\cos \theta & -\sin \theta & tx\\ \sin \theta & \cos \theta & ty\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

3.代码示例

import numpy as np
import math

class GenkiArmForwardKinematics:
    def __init__(self):
        """
        初始化Genki机械臂的正向运动学求解器
        根据URDF文件定义的DH参数和关节配置
        """
        # 关节偏移量 (来自URDF文件的origin标签)
        self.joint_offsets = [
            np.array([-0.013, 0, 0.0265]),    # Joint 1 (腰部旋转)
            np.array([0.081, 0, 0]),          # Joint 2 (大臂控制)
            np.array([0, 0, 0.118]),          # Joint 3 (小臂控制)
            np.array([0, 0, 0.118]),          # Joint 4 (腕部控制)
            np.array([0, 0, 0.0653]),         # Joint 5 (腕部旋转)
            np.array([0, -0.0132, 0.021])     # Joint 6 (夹爪控制)
        ]
        
        # 关节轴向量 (来自URDF文件的axis标签)
        self.joint_axes = [
            np.array([1, 0, 0]),    # Joint 1: x轴旋转
            np.array([0, 1, 0]),    # Joint 2: y轴旋转
            np.array([0, 1, 0]),    # Joint 3: y轴旋转
            np.array([0, 1, 0]),    # Joint 4: y轴旋转
            np.array([0, 0, 1]),    # Joint 5: z轴旋转
            np.array([1, 0, 0])     # Joint 6: x轴旋转
        ]
        
        # 关节角度偏移 (来自URDF文件的rpy标签)
        self.joint_rpy_offsets = [
            np.array([0, -1.57, 0]),    # Joint 1
            np.array([0, 1.57, 0]),     # Joint 2
            np.array([0, 0, 0]),        # Joint 3
            np.array([0, 0, 0]),        # Joint 4
            np.array([0, 0, 0]),        # Joint 5
            np.array([0, 0, 0])         # Joint 6
        ]

    def rotation_matrix_x(self, theta):
        """绕X轴旋转的变换矩阵"""
        cos_theta = math.cos(theta)
        sin_theta = math.sin(theta)
        return np.array([
            [1, 0, 0, 0],
            [0, cos_theta, -sin_theta, 0],
            [0, sin_theta, cos_theta, 0],
            [0, 0, 0, 1]
        ])

    def rotation_matrix_y(self, theta):
        """绕Y轴旋转的变换矩阵"""
        cos_theta = math.cos(theta)
        sin_theta = math.sin(theta)
        return np.array([
            [cos_theta, 0, sin_theta, 0],
            [0, 1, 0, 0],
            [-sin_theta, 0, cos_theta, 0],
            [0, 0, 0, 1]
        ])

    def rotation_matrix_z(self, theta):
        """绕Z轴旋转的变换矩阵"""
        cos_theta = math.cos(theta)
        sin_theta = math.sin(theta)
        return np.array([
            [cos_theta, -sin_theta, 0, 0],
            [sin_theta, cos_theta, 0, 0],
            [0, 0, 1, 0],
            [0, 0, 0, 1]
        ])

    def translation_matrix(self, x, y, z):
        """平移变换矩阵"""
        return np.array([
            [1, 0, 0, x],
            [0, 1, 0, y],
            [0, 0, 1, z],
            [0, 0, 0, 1]
        ])

    def get_joint_transform(self, joint_index, angle):
        """
        计算单个关节的齐次变换矩阵
        """
        # 获取关节参数
        offset = self.joint_offsets[joint_index]
        axis = self.joint_axes[joint_index]
        rpy_offset = self.joint_rpy_offsets[joint_index]
        
        # 构建变换矩阵
        # 1. 先应用RPY偏移
        T_rpy = np.eye(4)
        if rpy_offset[0] != 0:  # roll
            T_rpy = T_rpy @ self.rotation_matrix_x(rpy_offset[0])
        if rpy_offset[1] != 0:  # pitch
            T_rpy = T_rpy @ self.rotation_matrix_y(rpy_offset[1])
        if rpy_offset[2] != 0:  # yaw
            T_rpy = T_rpy @ self.rotation_matrix_z(rpy_offset[2])
        
        # 2. 应用关节旋转
        T_joint = np.eye(4)
        if joint_index == 0:  # Joint 1: 绕X轴旋转
            T_joint = self.rotation_matrix_x(angle)
        elif joint_index in [1, 2, 3]:  # Joints 2,3,4: 绕Y轴旋转
            T_joint = self.rotation_matrix_y(angle)
        elif joint_index == 4:  # Joint 5: 绕Z轴旋转
            T_joint = self.rotation_matrix_z(angle)
        elif joint_index == 5:  # Joint 6: 绕X轴旋转
            T_joint = self.rotation_matrix_x(angle)
        
        # 3. 应用平移
        T_translate = self.translation_matrix(offset[0], offset[1], offset[2])
        
        # 组合变换: RPY偏移 -> 关节旋转 -> 平移
        T_total = T_translate @ T_rpy @ T_joint
        
        return T_total

    def forward_kinematics(self, joint_angles):
        """
        正向运动学求解
        
        参数:
            joint_angles: 包含6个关节角度的列表或数组，单位为弧度
                         [j1, j2, j3, j4, j5, j6]
        
        返回:
            末端执行器的XYZ坐标 [x, y, z]
        """
        if len(joint_angles) != 6:
            raise ValueError("必须提供6个关节角度")
        
        # 初始化总的变换矩阵为单位矩阵
        T_total = np.eye(4)
        
        # 依次计算每个关节的变换并累乘
        for i in range(6):
            T_joint = self.get_joint_transform(i, joint_angles[i])
            T_total = T_total @ T_joint
            print(f"Joint {i+1} 变换矩阵:")
            print(T_joint)
            print()
        
        # 提取末端位置坐标
        end_effector_position = T_total[:3, 3]
        
        return end_effector_position

    def demo(self):
        """演示函数"""
        print("=== Genki机械臂正向运动学演示 ===\n")
        
        # 示例关节角度 (弧度)
        test_angles = [0, 0, 0, 0, 0, 0]  # 所有关节在零位
        print(f"输入关节角度: {test_angles}")
        
        try:
            position = self.forward_kinematics(test_angles)
            print(f"末端位置坐标: x={position[0]:.4f}, y={position[1]:.4f}, z={position[2]:.4f}")
        except Exception as e:
            print(f"计算出错: {e}")

def main():
    # 创建运动学求解器实例
    arm = GenkiArmForwardKinematics()
    
    # 运行演示
    arm.demo()
    
    # 交互式测试
    print("\n=== 交互式测试 ===")
    while True:
        try:
            print("\n请输入6个关节角度(弧度)，用空格分隔:")
            print("例如: 0 0.5 -0.3 0.2 -0.1 0")
            user_input = input("关节角度: ")
            
            if user_input.lower() == 'quit':
                break
                
            angles = list(map(float, user_input.split()))
            
            if len(angles) != 6:
                print("错误: 必须输入6个角度值")
                continue
            
            position = arm.forward_kinematics(angles)
            print(f"\n末端位置坐标:")
            print(f"  X: {position[0]:.6f} 米")
            print(f"  Y: {position[1]:.6f} 米") 
            print(f"  Z: {position[2]:.6f} 米")
            print(f"  距离原点: {np.linalg.norm(position):.6f} 米")
            
        except ValueError:
            print("错误: 请输入有效的数字")
        except KeyboardInterrupt:
            print("\n程序退出")
            break
        except Exception as e:
            print(f"计算错误: {e}")

if __name__ == "__main__":
    main()

二、IK（运动学逆解）

运动学逆解即为：从任务空间到关节空间。然而对比与FK的唯一性，确定性，IK可能无解、单解或多解。其特性有：

1. 多解性：同一目标，可能存在多种姿态。这个比较好理解，够一个东西，可以有多条线路，机器臂有多种抬法。
2. 无解性：这要求目标必须在工作空间内（可以这么理解：机器人的胳膊长度不够，够不到，无解，机器人的肢体跟人一样，有盲区，比如人的舌头舔不到胳膊肘，这也是无解）
3. 奇异性：特定位形丢失自由度，这很危险，需要主动规避。这个可以理解为，手臂伸直了，往肩这个方向，向里就收缩不动，这个方向就是奇异点。用数学解释即：雅可比矩阵降秩 → 不可逆 → 逆解算不出 / 无穷大 / 爆炸

"""
Genki机械臂逆向运动学 - 实用示例版本
包含工作空间检查和合理的目标位置示例
"""

import numpy as np
import math
from scipy.optimize import minimize

def inverse_kinematics(target_xyz):
    """
    Genki机械臂逆向运动学求解
    
    参数:
        target_xyz: [x, y, z] 目标位置坐标(米)
    
    返回:
        [j1, j2, j3, j4, j5, j6] 关节角度(度数)
    """
    
    def fk(joint_angles_deg):
        """正向运动学"""
        angles = [math.radians(a) for a in joint_angles_deg]
        
        joints = [
            {'axis': 'x', 'offset': [-0.013, 0, 0.0265], 'rpy': [0, -1.57, 0]},
            {'axis': 'y', 'offset': [0.081, 0, 0], 'rpy': [0, 1.57, 0]},
            {'axis': 'y', 'offset': [0, 0, 0.118], 'rpy': [0, 0, 0]},
            {'axis': 'y', 'offset': [0, 0, 0.118], 'rpy': [0, 0, 0]},
            {'axis': 'z', 'offset': [0, 0, 0.0653], 'rpy': [0, 0, 0]},
            {'axis': 'x', 'offset': [0, -0.0132, 0.021], 'rpy': [0, 0, 0]}
        ]
        
        def rot(axis, angle):
            c, s = math.cos(angle), math.sin(angle)
            if axis == 'x': return np.array([[1,0,0],[0,c,-s],[0,s,c]])
            elif axis == 'y': return np.array([[c,0,s],[0,1,0],[-s,0,c]]) 
            elif axis == 'z': return np.array([[c,-s,0],[s,c,0],[0,0,1]])
        
        T = np.eye(4)
        for angle, joint in zip(angles, joints):
            # RPY偏移
            R_rpy = np.eye(3)
            if joint['rpy'][0] != 0: R_rpy = R_rpy @ rot('x', joint['rpy'][0])
            if joint['rpy'][1] != 0: R_rpy = R_rpy @ rot('y', joint['rpy'][1])
            if joint['rpy'][2] != 0: R_rpy = R_rpy @ rot('z', joint['rpy'][2])
            
            # 关节旋转
            R_joint = rot(joint['axis'], angle)
            R = R_rpy @ R_joint
            
            # 齐次变换
            Ti = np.eye(4)
            Ti[:3,:3] = R
            Ti[:3,3] = joint['offset']
            T = T @ Ti
        
        return T[:3, 3]
    
    def objective(joint_angles, target):
        """目标函数"""
        pos = fk(joint_angles)
        error = np.array(pos) - np.array(target)
        return np.sum(error**2)
    
    # 关节限制 (度数)
    bounds = [(-90, 90), (-90, 90), (-90, 90), (-90, 90), (-90, 90), (0, 90)]
    
    # 多次初始猜测以提高成功率
    initial_guesses = [
        [0, 0, 0, 0, 0, 0],
        [30, -30, 30, -30, 30, 0],
        [-30, 30, -30, 30, -30, 0],
        [45, -45, 45, -45, 45, 0]
    ]
    
    best_result = None
    best_error = float('inf')
    
    for guess in initial_guesses:
        result = minimize(
            fun=objective,
            x0=guess,
            args=(target_xyz,),
            method='L-BFGS-B',
            bounds=bounds,
            options={'disp': False}
        )
        
        final_pos = fk(result.x)
        error = np.linalg.norm(np.array(final_pos) - np.array(target_xyz))
        
        if error < best_error:
            best_error = error
            best_result = result
    
    if best_result is not None:
        final_angles = best_result.x.tolist()
        final_position = fk(final_angles)
        return {
            'joint_angles': final_angles,
            'final_position': final_position.tolist(),
            'position_error': best_error,
            'success': best_error < 0.01  # 1cm以内认为成功
        }
    else:
        return {'success': False, 'message': '无法找到解'}

# 实用示例函数
def solve_position(x, y, z):
    """求解指定位置的关节角度"""
    print(f"\n🎯 目标位置: X={x:.3f}m, Y={y:.3f}m, Z={z:.3f}m")
    
    result = inverse_kinematics([x, y, z])
    
    if result['success']:
        print("✅ 求解成功!")
        print("关节角度:")
        joint_names = ['腰部旋转', '大臂控制', '小臂控制', '腕部控制', '腕部旋转', '夹爪控制']
        for i, (name, angle) in enumerate(zip(joint_names, result['joint_angles']), 1):
            print(f"  {i}. {name}: {angle:.2f}°")
        
        final_pos = result['final_position']
        print(f"\n📍 实际到达位置:")
        print(f"  X: {final_pos[0]:.4f}m")
        print(f"  Y: {final_pos[1]:.4f}m") 
        print(f"  Z: {final_pos[2]:.4f}m")
        print(f"📏 位置误差: {result['position_error']:.4f}m")
    else:
        print("❌ 求解失败 - 目标位置可能超出工作空间")
    
    return result

def demo_common_positions():
    """演示常见工作位置"""
    print("=== Genki机械臂逆向运动学演示 ===")
    print("展示机械臂可达的典型工作位置\n")
    
    # 测试位置集合
    test_positions = [
        # 基本位置
        (0.0, 0.0, 0.4),      # 正前方中等高度
        (0.1, 0.0, 0.35),     # 右侧中等高度
        (-0.1, 0.0, 0.35),    # 左侧中等高度
        (0.0, 0.1, 0.3),      # 前方较高位置
        (0.0, -0.1, 0.25),    # 后方较低位置
        
        # 工作区域位置
        (0.05, 0.05, 0.32),   # 右前方
        (-0.05, 0.05, 0.32),  # 左前方
        (0.08, -0.03, 0.28),  # 右后方
        (-0.08, -0.03, 0.28), # 左后方
        
        # 边界测试
        (0.12, 0.0, 0.2),     # 右侧边界
        (-0.12, 0.0, 0.2),    # 左侧边界
        (0.0, 0.15, 0.25),    # 前方边界
    ]
    
    successful = 0
    total = len(test_positions)
    
    for x, y, z in test_positions:
        result = solve_position(x, y, z)
        if result['success']:
            successful += 1
    
    print(f"\n📊 求解统计:")
    print(f"  测试位置总数: {total}")
    print(f"  成功求解数量: {successful}")
    print(f"  成功率: {successful/total*100:.1f}%")

def interactive_solver():
    """交互式求解器"""
    print("\n=== 交互式位置求解器 ===")
    print("请输入目标位置坐标 (米)")
    print("格式: X Y Z (用空格分隔)")
    print("例如: 0.1 0.05 0.3")
    print("输入 'demo' 查看演示，'quit' 退出\n")
    
    while True:
        try:
            user_input = input("目标位置: ").strip()
            
            if user_input.lower() == 'quit':
                print("👋 程序退出")
                break
            elif user_input.lower() == 'demo':
                demo_common_positions()
                continue
            
            coords = list(map(float, user_input.split()))
            
            if len(coords) != 3:
                print("❌ 错误: 请提供3个坐标值")
                continue
            
            x, y, z = coords
            solve_position(x, y, z)
            print("-" * 50)
            
        except ValueError:
            print("❌ 输入格式错误，请输入数字")
        except KeyboardInterrupt:
            print("\n👋 程序被用户中断")
            break
        except Exception as e:
            print(f"❌ 计算错误: {e}")

if __name__ == "__main__":
    # 运行演示
    demo_common_positions()
    
    # 可选：启动交互式求解器
    # interactive_solver()

三、PID粗析

---

最后我们来简单了解一下PID控制器。首先，为了防止机器人出现“帕金森”，我们不仅要有大脑，还要用控制器。为此，诞生了Bang-Bang控制器和PID控制器，然而，Bang-Bang控制器会导致剧烈波动，所以目前主要用PID控制器。
P（Proportional）比例（永远到不了精确位置，到了，如果只有P控制，会立刻停止工作，然后又算误差，又开始工作）、I（Integral）积分、D（Derivative）微分

标准PID公式为：
$$u(t)=K_{p}e(t)+K_i{\int }_0^{t}e(\tau )d\tau +K_d\frac{de(t)}{dt}$$
其中：
e(t)：误差 = 目标值 - 当前值
Kp​：比例系数
Ki​：积分系数
Kd​：微分系数

在这个阶段，我暂且用这个例子辅助理解：
eg. 机器人关节从 0° 转到 100°

• 仅P 比例控制时，控制器会根据误差大小出力，离目标越远劲越大、越近劲越小，动作很快，但永远差一点到不了目标，存在稳定静差；
• 加上 I 积分控制后，只要还有误差，积分就会不断累加出力，把最后一点偏差慢慢补到 0，能精准到达目标位置，可是容易冲过头、来回晃动；
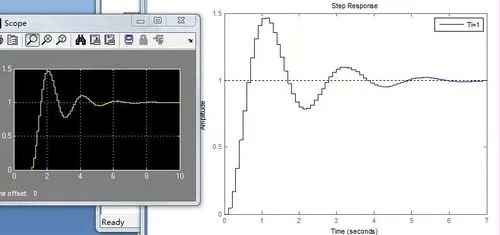
• 再加入 D 微分控制后，它能根据误差变化速度提前预判、起到刹车减震作用，既保留了 P 的快速、I 的精准，又避免了冲击与抖动，最终实现又快、又准、又平稳的控制效果，这就是完整 PID 控制器的作用。

个人感觉可以从比例、积分、微分的角度进一步在实际应用中细细品味。

总结

初编2026/2/15。个人对自己的要求是，这一章是一个大致框架，明确了后续深度研究的基础，后续有更多理解了再补充吧。本人才疏学浅，敬请批评指正，欢迎大家交流看法。