第12 章 激光雷达 + IMU 组合定位

12.1 引言

第11章介绍的激光里程计算法仅通过激光点云估计激光雷达的运动状态，其精度受周围环境及激光雷达点云质量的影响较大。IMU（Inertial Measurement Unit）是机器人和汽车领域常用的测量车辆运动状态的传感器，其主要包含陀螺仪和加速度计，可以较高的频率（如 $40\sim 500\mathrm{Hz}$ ）输出被测物体的角速度以及加速度，并可通过积分的方式进一步得到一段时间内车辆的姿态和位置变化。但IMU在实际工作时，由于各种不可避免的干扰因素，会导致陀螺仪及加速度计产生误差，其导航误差将随时间而增大，因此通常需要利用外部信息进行辅助，通过组合导航的方式来提升IMU定位的准确性[1]。另外，由于激光里程计频率较低（通常为 $10\mathrm{Hz}$ ），且主要通过对环境的感知来实现对自车的定位估计，而IMU具有较高的频率，其通过对自身运动状态量的积分实现位姿估计，二者在一定程度上具有互补性，因此许多学者尝试将激光里程计和IMU组合起来以实现高精度的实时定位。根据二者组合方式和原理的不同，业界通常将此细分为LiDAR+IMU松耦合以及LiDAR+IMU紧耦合两个研究方向。

1. 激光雷达与IMU松耦合定位

该类别的组合定位算法通常使激光里程计和IMU航位推算相互独立运行，并基于卡尔曼滤波框架、粒子滤波框架等实现二者信息的融合，最终输出定位估计结果。例如，国防科技大学的H.Xue等人[2]于2019年提出了IMU-AHFLO算法，旨在使用基于点线特征或点云分布特征匹配的激光里程计得到车辆在两帧点云对应时刻内位姿变化的观测值，然后利用高频的IMU数据结合车辆运动学方程得到上述时刻位姿变化的预测值，最后使用卡尔曼滤波器对车辆的位姿状态进行估计。南昌大学的廖杰华[3]则尝试结合LOAM算法[34]和自适应粒子滤波算法，用于无人物流小车的室内定位。Google发布的Cartographer算法[4-6]则采用分层优化的思路，在前端使用无迹卡尔曼滤波器实现2D激光雷达点云和IMU数据的松耦合，并在后端基于子地图构建优化问题，同时使用分支定界法[7]加速闭环检测过程的求解。

2. 激光雷达与IMU紧耦合定位

上述松耦合的定位方式虽然原理简单，但是人为地将激光雷达数据和IMU数据分开运算是造成一定程度的信息损失。因此，一些学者尝试对同一个位姿优化问题结合激光雷达数据和IMU数据来求解，即使用紧耦合的方式进行位姿估计[8,23]。激光雷达与IMU紧耦合定位具体又可细分为基于滤波器思想和基于平滑优化思想两种形式。

基于滤波器思想的紧耦合定位算法通常会在系统的状态更新过程中结合多传感器的数据[9]。例如，H. Sebastian等人[10]基于自适应扩展卡尔曼滤波器实现了3D激光雷达和GPS/INS的紧耦合，并被成功应用于无人小车的室外定位。但是由于滤波器对系统状态方程进行了线性化近似并且使用了递推过程，导致算法的线性化累积误差不断增大，算法的精度通常会随时间不断降低。为了改善这类算法的性能，香港科技大学机器人与多感知实验室的C.Qin等人在ICRA2020会议上提出了LINS算法，旨在使用迭代的误差状态卡尔曼滤波器实现激光雷达数据和IMU数据的紧耦合，并通过不断修正系统的状态误差来获取最优的位姿估计，实现对车辆实时的高精度定位和建图。香港大学Mars实验室在2021年和2022年分别提出了FAST-LIO

算法[33]和FAST-LIO2算法[34]，旨在通过迭代卡尔曼滤波框架，在状态迭代更新步骤中通过结合激光雷达数据和IMU数据构建非线性优化问题以实现紧耦合定位。

基于平滑优化思想的紧耦合定位算法通常将定位问题转为图论中的图模型表示，并基于最小二乘或非线性优化的方式来求解。业界常用的图模型有动态贝叶斯网络[14]、因子图模型[15,16]、马尔可夫随机场模型[17,18]等，近年来以因子图模型的使用最为广泛。例如，P.Geneva等人[19]在IROS2018会议上提出了Lips算法，旨在基于图优化框架结合激光雷达平面约束因子和IMU预积分因子[20]实现室内三维定位。H.Ye等人[21]在LIO-mapping算法中同样结合图优化框架实现了激光雷达和IMU的紧耦合定位，并提出了旋转约束建图方法来对最终的位姿和点云地图进行优化。此外，T.Shan等人在LIO-SAM算法[22]中进一步基于因子图模型实现了激光里程计因子、预积分因子及GPS因子的紧耦合，并且已被应用于多种测试平台。

下面我们将分别针对LiDAR + IMU的松耦合和紧耦合两种技术路线，具体选取两个算法进行学习。

12.2 IMU-AHFLO算法

本节选择LiDAR + IMU松耦合方案中较有代表性的IMU-Aided High-Frequency LiDAR Odometry（简称IMU-AHFLO）算法[2]进行展开。与紧耦合方案中涉及IMU预积分和因子图等理论相比，基于EKF的松耦合原理过程相对简单，为了加深读者的理解，本节将给出H. Xue等人在IMU-AHFLO算法中执行的公式推导过程。

我们的目的是结合IMU数据和激光雷达数据获取车辆的实时位姿，为此，我们首先需要定义算法求解过程中涉及的3个坐标系，具体如图12-1所示。

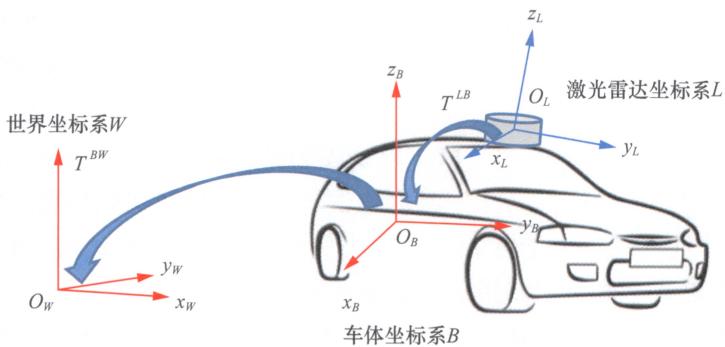
图12-1 IMU-AHFLO算法中各坐标系的定义

IMU-AHFLO算法中各坐标系的位置和朝向定义如下。

（1）世界坐标系 {W}\{W\}{W} ：世界坐标系为“东北天”坐标系，即 $x$ 轴指向东， $y$ 轴指向北， $z$ 轴朝上，世界坐标系的原点是事先给定的固定位置。
（2）车体坐标系 {B}\{B\}{B} ：车体坐标系与IMU坐标系一致，原点位于车辆后轴中心处， $x$ 轴沿着车辆后轴指向右侧，车头方向为 $y$ 轴， $z$ 轴朝上。
（3）激光雷达坐标系 {L}\{L\}{L} ：激光雷达坐标系的原点为激光雷达安装位置， $x$ 轴指向右侧，

前向为 $y$ 轴， $z$ 轴朝上。

本节使用 $T_k^{WB}$ 表示 $t_k$ 时刻由 {W}\{W\}{W} 坐标系运动到 {B}\{B\}{B} 坐标系的空间变换矩阵（上标读取顺序为从左向右），并有 $T_k^{WB}=(T_k^{BW}{)}^{-1}$ 。 $\Delta T_{k,k-1}^B$ 表示车辆在 $[t_{k-1},t_k]$ 时间内相对 {B}t−1\{B\}_{t-1}{B}t−1​ 坐标系的运动变化，并有

$$\Delta {\mathbf{T}}_{k,k-1}^B={\left({\mathbf{T}}_{k-1}^{WB}\right)}^{-1}\ast {\mathbf{T}}_k^{WB}\text{\hspace{1em}(12-1)}$$

其中 $T$ 为齐次变换矩阵，并有 $T=\left[\begin{array}{cc}R& p\\ 0& 1\end{array}\right]$ ， $R$ 为对应的旋转矩阵， $p$ 为位移矢量。

本节使用 $T_k^{WL}$ 表示 $t_k$ 时刻由 {W}\{W\}{W} 坐标系运动到 {L}\{L\}{L} 坐标系的空间变换矩阵，即激光雷达在世界坐标系下的位置。 $\Delta T_{k,k-1}^L$ 表示激光雷达在 $[t_{k-1},t_k]$ 时间内相对 {L}t−1\{L\}_{t-1}{L}t−1​ 坐标系的运动变化。 $T^{BL}$ 则表示由 {B}\{B\}{B} 坐标系运动到 {L}\{L\}{L} 坐标系的空间变换矩阵，此为激光雷达的外参，可利用前面章节中介绍的静态或动态标定算法得出。

12.2.1 IMU-AHFLO算法流程

在IMU-AHFLO算法中，IMU和轮速计以 $100\mathrm{Hz}$ 的频率运行，激光里程计以 $10\mathrm{Hz}$ 的频率运行，激光里程计和IMU/轮速计的耦合流程如图12-2所示。

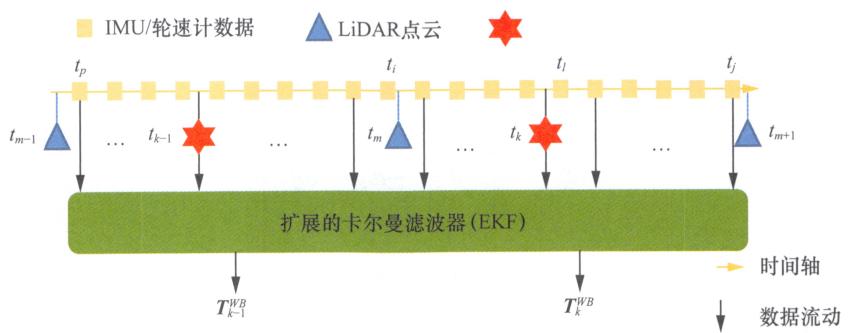
图12-2 激光里程计和IMU/轮速计的耦合流程

观察图12-2，在 $t_{m-1}$ 、 $t_m$ 和 $t_{m+1}$ 时刻，我们分别获取到第 $m-1$ 帧、第 $m$ 帧和第 $m+1$ 帧点云，每两帧点云的时间间隔约为100毫秒，并且在此期间，我们通常可以得到10组IMU数据和轮速计数据。令 $t_i$ 和 $t_j$ 分别为第 $m$ 帧和第 $m+1$ 帧点云间IMU数据的起始时间戳和终止时间戳，且有 $t_m\approx t_i$ ， $t_{m+1}\approx t_j$ 。以第 $m$ 帧点云为研究对象，并假设我们已知车辆在 $t_{k-1}$ 时刻的位姿为 $T_{k-1}^{WB}$ 。一方面，基于 $t_{m-1}$ 和 $t_m$ 时刻的激光点云信息，我们可以采用NDT算法或LOAM算法中基于特征的点云匹配方法得到 $[t_{m-1},t_m]$ 时间内激光雷达的位置变换，并结合激光雷达外参，得到车体的相应位姿变化，作为车辆位姿的观测值。需要指出的是，缘于激光里程计的滞后性，通常我们在 $t_k$ 时刻才能获取到对应 $t_m$ 时刻的位姿状态。因此，考虑到激光里程计的上述滞后性，IMU-AHFLO算法基于激光里程计的输出结果，并结合 $[t_m,t_k]$ 时间内由IMU推算的车辆位置变化作为最终观测值，以希望更接近当前 $t_k$ 时刻车辆的真实状态。另一方面，基于车辆运动学方程并结合高频的IMU/轮速计数据，我们可以近似得到 $t_k$ 时刻车辆位置的状态预测值。最后，根据 $t_k$ 时刻车体位置的状态预测值和基于激光里程计得到的车体在 $t_k$ 时刻的位置观测值，结合EKF算法即可得到 $t_k$ 时刻车辆位置的最终估计值 $T_k^{WB}$ 。状态预测和观测的具体推理过程我们将在本章后续部分详细展开。

12.2.2 基于IMU/轮速计的车辆位姿估计

图12-3给出了简化的车辆运动模型，IMU安装在车辆后轴中心，IMU坐标系的定义与车体坐标系的定义一致，两个轮速计分别安装在两个后轮处。小车由 $t_{k-1}$ 时刻位置行驶至 $t_k$ 时刻位置，其间，左、右轮速计输出的行驶距离分别为 $\Delta s_l$ 和 $\Delta s_r$ ，IMU输出的三个轴向角速度信息为 ${}_B{\omega }_k^{WB}=[{\omega }_k^x,{\omega }_k^y,{\omega }_k^z{]}^{\mathrm{T}}$ ， ${}_B{\omega }_k^{WB}$ 是车体坐标系相对世界坐标系的旋转角速度在当前车体坐标系下的表示。H.Xue等人在IMU-AHFLO算法中利用IMU输出的角速度信息估计车辆的姿态，并结合轮速计数据估计车辆的位移。

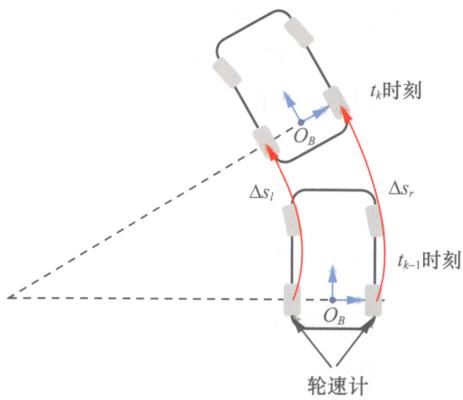
图12-3 车辆运动模型示意图

1. 角度维度

对于IMU的角速度数据，基于车辆运动学公式[24]，我们可以得到：

$$\frac{\mathrm{d}{\mathbf{R}}_k^{WB}}{\mathrm{d}t}={\mathbf{R}}_k^{WB}{\left[\begin{array}{l}{\omega }_k^x\\ {\omega }_k^y\\ {\omega }_k^z\end{array}\right]}^{\wedge }\text{\hspace{1em}(12-2)}$$

其中 $\hat{\Lambda }$ 表示反对称阵操作，并有

$${\left[\begin{array}{l}{\omega }_k^x\\ {\omega }_k^y\\ {\omega }_k^z\end{array}\right]}^{\wedge }=\left[\begin{array}{ccc}0& -{\omega }_k^z& {\omega }_k^y\\ {\omega }_k^z& 0& -{\omega }_k^x\\ -{\omega }_k^y& {\omega }_k^x& 0\end{array}\right]\text{\hspace{1em}(12-3)}$$

假设车辆在 $[t_{k-1},t_k]$ 时间内的角速度为常量，在 $[t_{k-1},t_k]$ 时间内对式（12-2）求积分，并求得该微分方程的解为

$${\mathbf{R}}_k^{WB}={\mathbf{R}}_{k-1}^{WB}\exp \left({\left({}_B{\omega }_k^{WB}\Delta t\right)}^{\wedge }\right)\text{\hspace{1em}(12-4)}$$

其中 $\Delta t=t_k-t_{k-1}$

由此，我们可以结合上一时刻 $t_{k-1}$ 车辆的姿态 $R_{k-1}^{WB}$ 和 IMU 的角速度数据 ${}_B{\omega }_k^{WB}$ ，推算得到当前时刻 $t_k$ 车辆的姿态 $R_k^{WB}$ 。

2. 位移维度

IMU-AHFLO算法利用轮速计信息推算车辆位置。由于左、右两侧轮速计输出的行驶距离分别为 $\Delta s_l$ 和 $\Delta s_r$ ，令 $\Delta s$ 为二者的平均值，则 $\Delta s$ 表示车辆在车体坐标系下的相对位移。假设车辆在 $[t_{k-1},t_k]$ 时间内的速度为常量，并且有 $v=\Delta s/(t_k-t_{k-1})$ ，由于轮速计仅能够记录沿着车头方向的位移，在 $[t_{k-1},t_k]$ 时间内，我们近似忽略了其他方向的运动，因此可以得到当前车体坐标系下车辆的速度矢量 $v_k^B=[\nu ,0,0{]}^{\mathrm{T}}$ 。进一步地，也可以得到车体坐标系下车辆的速度矢量。在世界坐标系下，车辆速度矢量之间的关系可以表示为

$${\mathbf{v}}_k^W={\mathbf{R}}_k^{WB}{\mathbf{v}}_k^B\text{\hspace{1em}(12-5)}$$

因此，结合车辆前一时刻的位置矢量 $p_{k-1}^{WB}$ 、车辆的姿态 ${\mathbf{R}}_k^{WB}$ 和车辆的速度矢量 ${\nu }_k^W$ ，可以

得到当前时刻车辆的位置为

$${\mathbf{p}}_k^{WB}={\mathbf{p}}_{k-1}^{WB}+{\mathbf{v}}_k^W\left(t_k-t_{k-1}\right)={\mathbf{p}}_{k-1}^{WB}+{\mathbf{R}}_k^{WB}[\Delta s,0,0{]}^{\mathrm{T}}\text{\hspace{1em}(12-6)}$$

12.2.3 基于EKF的松耦合过程

在第10章介绍的多目标跟踪模块中，我们已经接触过EKF的一些概念，下面我们将具体介绍EKF的基本原理和过程，进而详细分析IMU-AHFLO算法利用EKF实现激光里程计和IMU/轮速计松耦合的过程。同样，这里的讨论将涉及系统状态估计的基本知识，但是考虑到篇幅和本节侧重点，我们不再展开介绍，需要了解系统状态估计相关基础知识的读者可参考《现代控制理论》《视觉SLAM十四讲》等图书。

1. EKF的基本原理

EKF（Extended Kalman Filter）是经典的系统状态估计方法，在控制、数据融合等领域得到了广泛应用。EKF是KF（Kalman Filter）在非线性问题中的扩展，因此EKF同KF一样，也假设系统状态变量和观测变量均符合高斯分布，并且通常也由“预测”和“更新”两个步骤组成。

假设 $t_k$ 时刻非线性系统的状态变量为 $x_k$ ，观测变量为 $z_k$ ，系统状态方程 $f$ 和观测方程 $h$ 均是非线性的。在预测步骤中，我们希望通过系统状态方程和上一时刻系统的后验状态 ${\hat{x}}_{k-1}$ ，可以得到当前时刻系统状态的先验估计。具体来说，EKF 使用一阶泰勒展开公式将系统状态方程在 ${\hat{x}}_{k-1}$ 处做了线性化近似，故有预测步骤的状态递推公式：

$${\bar{x}}_k\approx f\left({\hat{x}}_{k-1}\right)+\frac{\partial f}{\partial x_{k-1}}{\mid }_{{\hat{x}}_{k-1}}\left(x_{k-1}-{\hat{x}}_{k-1}\right)\text{\hspace{1em}(12-7)}$$

$${\bar{\mathbf{P}}}_k=\mathbf{F}{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}^{\mathrm{T}}+\mathbf{R}$$

其中 ${\overline{\mathbf{x}}}_k$ 和 ${\overline{\mathbf{P}}}_k$ 为 $t_k$ 时刻系统状态 ${\mathbf{x}}_k$ 的先验高斯分布的均值矩阵和方差矩阵， $\mathbf{R}$ 为系统噪声的方差矩阵， ${\hat{\mathbf{x}}}_{k-1}$ 和 ${\hat{\mathbf{P}}}_{k-1}$ 为 $t_{k-1}$ 时刻系统状态 ${\mathbf{x}}_{k-1}$ 的后验高斯分布的均值矩阵和方差矩阵， $\mathbf{F}$ 为系统状态方程在 ${\hat{\mathbf{x}}}_{k-1}$ 处的雅克比矩阵，又称为状态转移矩阵，且有

$$F=\frac{\partial f}{\partial x_{k-1}}{\mid }_{{\hat{x}}_{k-1}}\text{\hspace{1em}(12-8)}$$

在更新步骤中，结合当前状态 $x_k$ 的先验预测值 ${\overline{x}}_k$ 和当前的系统观测值 $z_k$ ，可以估计当前系统的后验状态 ${\hat{x}}_k$ ，同样使用一阶泰勒展开公式将系统观测方程在 ${\overline{x}}_k$ 处做线性化近似，即有

$${\mathbf{K}}_k={\bar{\mathbf{P}}}_k{\mathbf{H}}^{\mathrm{T}}{\left(\mathbf{H}{\bar{\mathbf{P}}}_k{\mathbf{H}}^{\mathrm{T}}+\mathbf{Q}\right)}^{-1}$$

$${\hat{\mathbf{x}}}_k={\bar{\mathbf{x}}}_k+{\mathbf{K}}_k\left({\mathbf{z}}_k-h({\bar{\mathbf{x}}}_k)\right)\text{\hspace{1em}(12-9)}$$

$${\hat{\mathbf{P}}}_k=(\mathbf{I}-{\mathbf{K}}_k\mathbf{H}){\bar{\mathbf{P}}}_k$$

其中 $Q$ 为测量噪声的方差矩阵， $K_k$ 为卡尔曼增益， ${\hat{x}}_k$ 和 ${\hat{P}}_k$ 分别为系统状态 $x_k$ 的后验高斯分布的均值矩阵和方差矩阵。 $H$ 为系统观测方程在 ${\overline{\mathbf{x}}}_k$ 处的雅克比矩阵，又称为观测矩阵，且有

$$z_k\approx h\left({\bar{x}}_k\right)+\frac{\partial h}{\partial x_k}{\mid }_{{\bar{x}}_k}\left(x_k-{\bar{x}}_k\right)\text{\hspace{1em}(12-10)}$$

$$\mathbf{H}=\frac{\partial h}{\partial x_k}{|}_{{\bar{x}}_k}$$

2. IMU-AHFLO算法的车辆状态方程

具体到车辆的位姿估计问题，令车辆在 $t_k$ 时刻的状态变量为

$${\mathbf{x}}_k={\left[{\theta }_k^{WB},{\mathbf{p}}_k^{WB}\right]}^{\mathrm{T}}\text{\hspace{1em}(12-11)}$$

其中 ${\theta }_k^{WB}=[{\theta }_k^x,{\theta }_k^y,{\theta }_k^z{]}^{\mathrm{T}}$ 为车辆在世界坐标系下的姿态角矢量，根据罗德里格斯旋转公式，我们可以得到 $R_k^{WB}$ 和 ${\theta }_k^{WB}$ 之间的关系如下：

$${\mathbf{R}}_k^{WB}=\cos \left({\theta }_k^{WB}\right)\ast \mathbf{I}+\left(1-\cos \left({\theta }_k^{WB}\right)\ast {\mathbf{n}}_k\ast {\mathbf{n}}_k^{\mathrm{T}}\right)+\sin \left({\theta }_k^{WB}\right)\ast {\hat{\mathbf{n}}}_k\text{\hspace{1em}(12-12)}$$

其中 ${\theta }_k^{WB}=\sqrt{({\theta }_k^x{)}^2+({\theta }_k^y{)}^2+({\theta }_k^z{)}^2}$ ， $n_k={\theta }_k^{WB}/{\theta }_k^{WB}$ ， $n_k^{\wedge }$ 为 $n_k$ 的反对称阵。

结合式（12-12）和群论以及量子力学中常用的BCH（Baker-Campbell-Hausdorff）公式[26]，我们可以将李群空间中表示的车辆姿态递推公式［见式（12-4）］改写为对应李代数空间中状态变量 ${\theta }_k^{WB}$ 的表示形式，即有

$${\mathbf{\theta }}_k^{WB}={\mathbf{\theta }}_{k-1}^{WB}+{\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)\ast \left({}_B{\mathbf{\omega }}_k^{WB}\Delta t\right)\text{\hspace{1em}(12-13)}$$

其中 $J_l({\theta }_{k-1}^{WB})$ 为李群 ${\theta }_{k-1}^{WB}$ 的左雅克比，并有

$$J_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)=\frac{{\mathbf{\theta }}_{k-1}^{WB}}{2}\cot \left(\frac{{\mathbf{\theta }}_{k-1}^{WB}}{2}\right)\mathbf{I}+\left(1-\frac{{\mathbf{\theta }}_{k-1}^{WB}}{2}\cot \left(\frac{{\mathbf{\theta }}_{k-1}^{WB}}{2}\right)\right){\mathbf{n}}_k{\mathbf{n}}_k^{\mathrm{T}}\text{\hspace{1em}(12-14)}$$

由式（12-13）和式（12-6），我们可以得到车辆状态方程为

$${\mathbf{x}}_k={\mathbf{x}}_{k-1}+\left[\begin{array}{c}{\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)\ast \left({}_B{\mathbf{\omega }}_k^{WB}\Delta t\right)\\ {\mathbf{R}}_k^{WB}(1:3,1)\ast \Delta s\end{array}\right]\text{\hspace{1em}(12-15)}$$

结合式（12-8），我们可以求得EKF预测过程中的系统状态转移矩阵，即有

$$\mathbf{F}=\left[\begin{array}{ll}{\mathbf{F}}_{\theta \theta }& 0_{3\times 3}\\ {\mathbf{F}}_{p\theta }& {\mathbf{I}}_{3\times 3}\end{array}\right]\in {\mathbb{R}}^{6\times 6}\text{\hspace{1em}(12-16)}$$

其中：

$${\mathbf{F}}_{\theta \theta }={\mathbf{I}}_{3\times 3}+{\left[\begin{array}{l}{\left(\frac{\partial {\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)}{\partial {\theta }_{k-1}^x}{\ast }_B{\mathbf{\omega }}_k^{WB}\Delta t\right)}^{\mathrm{T}}\\ {\left(\frac{\partial {\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)}{\partial {\theta }_{k-1}^y}{\ast }_B{\mathbf{\omega }}_k^{WB}\Delta t\right)}^{\mathrm{T}}\\ {\left(\frac{\partial {\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_{k-1}^{WB}\right)}{\partial {\theta }_{k-1}^z}{\ast }_B{\mathbf{\omega }}_k^{WB}\Delta t\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\text{\hspace{1em}(12-17)}$$

$${\mathbf{F}}_{p\theta }={\mathbf{I}}_{3\times 3}+\left[\frac{\partial {\mathbf{R}}_k^{WB}(1:3,1)}{\partial {\theta }_{k-1}^x},\frac{\partial {\mathbf{R}}_k^{WB}(1:3,1)}{\partial {\theta }_{k-1}^y},\frac{\partial {\mathbf{R}}_k^{WB}(1:3,1)}{\partial {\theta }_{k-1}^z}\right]\ast \Delta s$$

3. IMU-AHFLO算法的车辆观测方程

假设选择的观测变量为

$${\mathbf{z}}_k={\left[{\mathbf{\theta }}_k^{WB},{\mathbf{p}}_k^{WB}\right]}^{\mathrm{T}}\text{\hspace{1em}(12-18)}$$

若将激光里程计的输出直接作为观测结果，则观测矩阵具体为

$$H=I_{6\times 6}\text{\hspace{1em}(12-19)}$$

但是，我们需要考虑激光里程计计算结果的滞后性。如图12-2所示，激光里程计旨在计算由 $t_m$ 时刻的点云进行匹配得到的车辆位姿观测结果，计算过程直到 $t_k$ 时刻才结束并输出给EKF，这段时间内车辆的运动可近似基于 $[t_i,t_l]$ 时间内IMU/轮速计的信息进行补偿。令 $\Delta {\xi }_{i,j}=[\Delta {\theta }_{i,l},\Delta p_{i,l}{]}^{\mathrm{T}}$ ，为进一步提升定位算法的准确性，H.Xue等人在IMU-AHFLO算法中使用了下述观测方程：

$${\mathbf{z}}_k=\left[\begin{array}{l}{\mathbf{\theta }}_m\\ {\mathbf{p}}_m\end{array}\right]+\left[\begin{array}{l}{\mathbf{J}}_l^{-1}\left({\mathbf{\theta }}_k^{WB}\right)\ast \left(\Delta {\mathbf{\theta }}_{i,l}\right)\\ \Delta {\mathbf{R}}_{i,j}^B(1:3,1)\ast \Delta {\mathbf{p}}_{i,l}\end{array}\right]\text{\hspace{1em}(12-20)}$$

对应的观测矩阵为

$$\mathbf{H}=\left[\begin{array}{ll}{\mathbf{H}}_{\theta \theta }& 0_{3\times 3}\\ 0_{3\times 3}& {\mathbf{H}}_{pp}\end{array}\right]\text{\hspace{1em}(12-21)}$$

其中 $H_{pp}=\Delta R_{i,l}^{WB}\in {\mathbb{R}}^{3\times 3}$ ， $H_{\theta \theta }\in {\mathbb{R}}^{3\times 3}$ 并可表示为

$${\mathbf{H}}_{\theta \theta }={\left[\begin{array}{l}{\left(\frac{\partial {\mathbf{J}}_l^{-1}({\mathbf{\theta }}_k)}{\partial {\theta }_k^x}\ast \Delta {\mathbf{\theta }}_{i,l}\right)}^{\mathrm{T}}\\ {\left(\frac{\partial {\mathbf{J}}_l^{-1}({\mathbf{\theta }}_k)}{\partial {\theta }_k^y}\ast \Delta {\mathbf{\theta }}_{i,l}\right)}^{\mathrm{T}}\\ {\left(\frac{\partial {\mathbf{J}}_l^{-1}({\mathbf{\theta }}_k)}{\partial {\theta }_k^z}\ast \Delta {\mathbf{\theta }}_{i,l}\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\text{\hspace{1em}(12-22)}$$

基于式（12-7）中的先验协方差矩阵 ${\overline{P}}_k$ 和式（12-20）中的观测矩阵 $H$ ，可由式（12-9）得到卡尔曼增益 $K_k$ 和系统状态的后验估计 ${\hat{x}}_k$ 。IMU-AHFLO算法的流程如表12-1所示。

表 12-1 IMU-AHFLO 算法的流程

输入: 车辆历史位置集合{T_i^{WB}}, IMU 数据和轮速计数据, 由激光里程计得到的车辆位置观测值T_{L_k}^{WB}, 上一帧_{t_{k-1}}时刻的车辆位置T_{k-1}^{WB}

输出: 当前帧_{t_k}时刻的车辆位置最终估计值T_k^{WB}

1. 利用T_{k-1}^{WB}和IMU/轮速计数据, 结合式(12-7)得到t_k时刻的车辆状态预测值x̅_k

2. if 获取到激光里程计数据T_{L_k}^{WB} then

3. 利用x̅_k和T_{L_k}^{WB}, 结合式(12-9)计算车辆的后验状态x̅_k并输出T_k^{WB}

4. end

5. else

6. 将预测值x̅_k作为当前车辆状态并输出T_k^{WB}

7. end

Xue等选取结构化道路场景和越野道路场景对IMU-AHFLO算法进行了测试验证。在结构化道路场景中，保持车辆行驶速度为 $25km/s$ ，总的行驶距离为 $1.1\mathrm{km}$ 。在越野道路场景中，保持车辆行驶速度为 $15km/s$ ，总的行驶距离为 $1.0\mathrm{km}$ 。IMU-AHFLO算法的输出轨迹和轨迹真值的对比结果如图12-4所示，该算法在结构化道路场景下的平均相对位置误差为 $0.31\%$ 在越野道路场景下的平均相对位置误差为 $0.93\%$

（a）结构化道路场景

轨迹真值 IMU-AHFLO算法的输出轨迹

图12-4 对比IMU-AHFLO算法在结构化道路场景和越野场景下的测试效果

起点 终点

（b）越野场景

（注：图片来自参考文献[2]）

12.2.4 算法小结

我们以IMU-AHFLO算法为例，详细分析了IMU和LiDAR经卡尔曼滤波框架进行松耦合定位的原理和过程。由于二者计算车辆位置的原理不同，失效形式也不同，因此通过二者的组合在一定程度上可以互补各自模块的缺点。具体来说，由于IMU/轮速计数据频率较高，激光里程计数据频率较低，因此在IMU-AHFLO算法中，我们选择基于IMU/轮速计数据结合汽车的运动状态方程，对车辆位置状态进行预测，并基于激光里程计的输出结果得到车辆位置状态的观测值，最终结合卡尔曼更新过程得到对应的后验状态估计值。

然而，这种松耦合的方式虽然原理和实现相对简单，但无法高效地利用IMU和LiDAR里程计数据，并且随着IMU测量偏差的不断累积，还会导致算法精度降低，此时IMU/LiDAR的紧耦合定位方法就派上用场了。