差速转向移动机器人基于速度的动力学模型与自适应控制器 MATLAB实现
差速转向移动机器人基于速度的动力学模型与自适应控制器 MATLAB实现
一、动力学模型构建
1. 运动学模型
差速转向机器人的核心是通过左右轮速度差实现转向。设:
- 轮距:LLL(两轮中心间距)
- 轮速:左轮 vlv_lvl、右轮 vrv_rvr
- 线速度:v=vl+vr2v=\frac{v_l+v_r}{2}v=2vl+vr
- 角速度:ω=vr−vlLω=\frac{v_r−v_l}{L}ω=Lvr−vl
位姿更新方程:
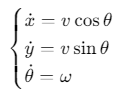
其中 x,y,θx,y,θx,y,θ为机器人位姿。
2. 动力学模型
考虑外部负载(如质量 mmm和转动惯量 III)的影响,动力学方程为:
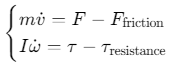
-
驱动力:F=(vr+vl)⋅r/2F=(v_r+v_l)⋅r/2F=(vr+vl)⋅r/2(rrr为轮半径)
-
摩擦力:Ffriction=μcsgn(v)+μvvF_{friction}=μ_csgn(v)+μ_vvFfriction=μcsgn(v)+μvv(库伦+粘滞摩擦)
-
转向阻力矩:τresistance=kt⋅ω2τ_{resistance}=k_t⋅ω^2τresistance=kt⋅ω2(与角速度平方相关)。
二、自适应控制器设计
1. 控制目标
跟踪参考轨迹 xref,yref,θrefx_{ref},y_{ref},θ_{ref}xref,yref,θref,最小化误差:
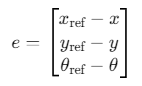
2. 自适应PID控制
通过在线调整 Kp,Ki,KdK_p,K_i,K_dKp,Ki,Kd适应负载变化:
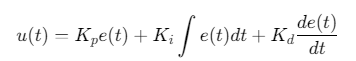
参数更新律(基于李雅普诺夫稳定性):
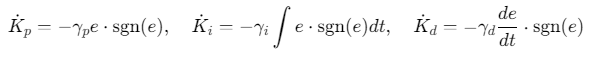
其中 γp,γi,γdγ_p,γ_i,γ_dγp,γi,γd为自适应增益。
3. 模型参考自适应控制(MRAC)
参考模型输出 ym(t)ym(t)ym(t)与实际输出 y(t)y(t)y(t)的误差驱动参数调整:
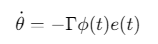
-
θθθ:控制器参数向量
-
ΓΓΓ:正定增益矩阵
-
ϕ(t)ϕ(t)ϕ(t):回归向量。
三、MATLAB仿真实现
1. 参数设置
% 机器人参数
L = 0.3; % 轮距 (m)
r = 0.05; % 轮半径 (m)
m = 2; % 质量 (kg)
I = 0.1; % 转动惯量 (kg·m²)
mu_c = 0.15; % 库伦摩擦系数
mu_v = 0.02; % 粘滞摩擦系数
Kt = 0.01; % 转向阻力系数
% 控制参数
Kp = 1.2; Ki = 0.3; Kd = 0.05; % 初始PID参数
gamma = 0.1; % 自适应增益
2. 动力学模型仿真
% 状态变量:[x, y, theta, v, omega]
state = [0; 0; 0; 0.5; 0.2]; % 初始状态
% 时间参数
dt = 0.01; % 时间步长
t_end = 10; % 仿真时间
t = 0:dt:t_end;
% 参考轨迹(圆形路径)
x_ref = 1.5*cos(0.2*t);
y_ref = 1.5*sin(0.2*t);
theta_ref = 0.2*t;
% 存储结果
x_hist = zeros(size(t));
y_hist = zeros(size(t));
theta_hist = zeros(size(t));
3. 自适应控制循环
for k = 1:length(t)
% 当前状态
x = state(1); y = state(2); theta = state(3);
v = state(4); omega = state(5);
% 计算控制输入(自适应PID)
e = [x_ref(k) - x; y_ref(k) - y; theta_ref(k) - theta];
u = Kp*e(1) + Ki*e(2) + Kd*e(3);
% 参数更新(李雅普诺夫律)
Kp = Kp - gamma * e(1) * sign(e(1));
Ki = Ki - gamma * e(2) * sign(e(2));
Kd = Kd - gamma * e(3) * sign(e(3));
% 动力学方程积分
F = (v + v) * r / 2; % 左右轮速度相同,无转向
F_friction = mu_c*sign(v) + mu_v*v;
tau = Kt * omega^2; % 转向阻力矩
dv = (F - F_friction)/m;
domega = (u - tau)/I;
% 更新状态
state(4) = v + dv*dt;
state(5) = omega + domega*dt;
state(1) = x + v*cos(theta)*dt;
state(2) = y + v*sin(theta)*dt;
state(3) = theta + omega*dt;
% 存储数据
x_hist(k) = state(1);
y_hist(k) = state(2);
theta_hist(k) = state(3);
end
4. 结果可视化
figure;
subplot(2,1,1);
plot(t, x_hist, 'r', t, x_ref, 'b--');
title('X方向跟踪效果');
xlabel('时间 (s)'); ylabel('位置 (m)');
legend('实际', '参考');
subplot(2,1,2);
plot(t, y_hist, 'g', t, y_ref, 'm--');
title('Y方向跟踪效果');
xlabel('时间 (s)'); ylabel('位置 (m)');
legend('实际', '参考');
参考代码 差速转向移动机器人基于速度的动力学模型与自适应控制器 www.youwenfan.com/contentcsr/100467.html
四、性能优化与调参
-
负载突变测试:
- 在 t=5t=5t=5秒时突增质量 m=5kgm=5kgm=5kg,观察自适应PID的恢复能力。
-
参数敏感性分析:
- 调整 γγγ值(如 0.05→0.20.05→0.20.05→0.2),对比收敛速度。
-
摩擦模型改进:
- 引入动态摩擦模型(如Stribeck摩擦),提升低速跟踪精度。
五、扩展应用
-
多传感器融合:
- 结合IMU和编码器数据,通过卡尔曼滤波估计状态。
-
路径规划结合:
- 使用A或RRT生成全局路径,再通过自适应控制器跟踪。
-
硬件在环仿真:
- 在ROS/Gazebo中搭建机器人模型,验证算法实时性。
六、总结
通过结合动力学模型与自适应PID控制,差速转向机器人可在负载变化下实现高精度轨迹跟踪。核心在于:
-
模型精确性:需考虑惯性、摩擦等非线性因素。
-
参数自适应:通过在线估计动态调整控制增益。
-
鲁棒性验证:需测试不同负载和干扰场景下的性能。

DAMO开发者矩阵,由阿里巴巴达摩院和中国互联网协会联合发起,致力于探讨最前沿的技术趋势与应用成果,搭建高质量的交流与分享平台,推动技术创新与产业应用链接,围绕“人工智能与新型计算”构建开放共享的开发者生态。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容






所有评论(0)