信息融合与状态估计 主要是针对多传感器多时滞（包括状态之后和观测滞后）系统，带有色噪声多重时滞传感网络系统的序列协方差交叉融合Kalman滤波器。 将带有色噪声的系统转化为带相关噪声的系统，然后再进行融合。

在现代自动化与机器人领域，信息融合与状态估计一直是研究热点。尤其是在多传感器多时滞系统中，如何高效地融合信息并准确估计系统状态，成为了许多研究者关注的问题。本文将探讨一种基于序列协方差交叉融合的卡尔曼滤波方法，特别适用于带有色噪声及多重时滞的传感网络系统。

多传感器多时滞系统概述

多传感器多时滞系统是指多个传感器同时对同一或不同目标进行信息采集，但传感器之间存在通信延迟或数据采集延迟。这种系统广泛应用于无人机导航、智能机器人定位、传感器网络等场景。然而，多传感器系统也面临着几个关键挑战：

1. 传感器间的通信延迟：不同传感器可能由于地理位置或其他因素导致数据传递时间不同。
2. 观测噪声的复杂性：传感器测量的数据中可能包含多种噪声，包括高斯噪声和非高斯噪声，甚至存在色噪声（即噪声具有非零的自相关性）。
3. 数据融合的实时性要求：在动态系统中，状态估计需要实时性，以支持快速决策。

色噪声与多重时滞的挑战

在实际应用中，多传感器系统往往面临以下问题：

• 色噪声：许多实际系统中的噪声并非白噪声，而是具有相关性的色噪声。这种相关性可能来源于传感器本身特性、环境因素或系统动态。
• 多重时滞：不仅传感器之间存在通信延迟，某些传感器可能需要经过多个中间节点才能将数据传输到主站，导致观测数据与状态更新的时间差。
• 状态与观测的滞后：有些传感器可能在状态更新后才发送数据，或者观测结果滞后于状态的变化。

这些问题使得传统的卡尔曼滤波方法难以直接应用，需要采用更为复杂的解决方案。

序列协方差交叉融合卡尔曼滤波方法

针对上述挑战，我们提出了一种基于序列协方差交叉融合的卡尔曼滤波方法。这种方法的核心思想是通过协方差矩阵的交叉融合，有效处理有色噪声和多重时滞问题。

方法原理

1. 模型构建：首先，我们需要建立系统的数学模型，包括状态转移模型和观测模型。由于存在色噪声，传统的高斯假设不再适用，因此需要引入协方差矩阵来描述噪声的统计特性。

1. 协方差交叉融合：在每个卡尔曼滤波步骤中，我们利用当前传感器的观测协方差和历史协方差信息，通过交叉融合的方式更新状态协方差矩阵。这种方法能够有效抑制色噪声的影响，并且能够处理观测时滞的问题。

1. 状态更新：基于更新后的协方差矩阵，通过卡尔曼增益计算，更新状态估计值。

代码实现

以下是一个简单的Python代码示例，展示了如何在实际数据上应用该方法：

import numpy as np

def sequence_covariance_fusion_kalman_filter measurements, sensors, process_noise, measurement_noise):
    """
    序列协方差交叉融合卡尔曼滤波器实现
    
    Args:
        measurements: 观测数据列表
        sensors: 感应器列表
        process_noise: 过程噪声协方差矩阵
        measurement_noise: 观测噪声协方差矩阵
        
    Returns:
        状态估计序列
    """
    n_states = sensors[0].state_dim
    n_sensors = len(sensors)
    state Estimates = []
    
    # 初始状态估计
    initial_state = np.zeros(n_states)
    initial_covariance = np.eye(n_states)
    
    state Estimates.append(initial_state)
    
    for measurement in measurements:
        # 更新过程噪声和观测噪声
        process_noise_current = process_noise
        measurement_noise_current = measurement_noise
        
        # 协方差交叉融合
        cross_covariance = np.cov(sensors[0].estimate - initial_state, rowvar=False)
        fused_covariance = cross_covariance * n_sensors
        
        # 卡尔曼增益计算
        kalman_gain = fused_covariance @ np.linalg.inv(fused_covariance + measurement_noise_current)
        
        # 状态更新
        state Estimates.append(state Estimates[-1] + kalman_gain @ (measurement - sensors[0].estimate))
        
        # 更新状态协方差
        initial_state = state Estimates[-1]
        initial_covariance = initial_covariance - kalman_gain @ fused_covariance @ initial_covariance
    
    return state Estimates

代码分析

1. 初始化：首先，我们初始化状态估计和协方差矩阵。这里假设初始状态为零向量，初始协方差矩阵为单位矩阵。

1. 过程噪声和观测噪声：我们需要定义系统的过程噪声和观测噪声协方差矩阵。这些矩阵描述了系统的不确定性。

1. 协方差交叉融合：在每个卡尔曼滤波步骤中，我们首先计算传感器之间的协方差交叉，然后将这些交叉协方差进行融合，得到一个更准确的状态协方差估计。

1. 卡尔曼增益计算：基于融合后的协方差矩阵，计算卡尔曼增益，用于更新状态估计。

1. 状态更新：利用卡尔曼增益和观测误差，更新状态估计值。

1. 协方差更新：最后，更新状态协方差矩阵，为下一个卡尔曼滤波步骤做准备。

方法优势

• 处理色噪声：通过协方差矩阵的交叉融合，能够有效抑制色噪声的影响。
• 处理多重时滞：通过序列更新的方式，能够逐步融合多传感器的数据，处理观测时滞问题。
• 实时性：方法具有较高的实时性，适用于需要实时状态估计的应用场景。

应用场景与挑战

应用场景

• 无人机导航：在无人机群飞中，多个无人机需要基于传感器数据协同导航，解决多时滞和有色噪声问题。
• 智能机器人定位：机器人需要基于多个传感器（如激光雷达、摄像头、IMU等）的数据进行定位，提高定位精度。
• 传感器网络：在大规模传感器网络中，数据融合是提高系统可靠性和精度的关键。

挑战

• 计算复杂度：协方差交叉融合计算量较大，需要优化算法以适应实时性要求。
• 噪声统计特性：如果噪声统计特性未知或变化较大，可能会影响融合效果。
• 传感器通信可靠性：在多传感器系统中，通信可靠性是一个关键问题，可能影响数据融合效果。

结论

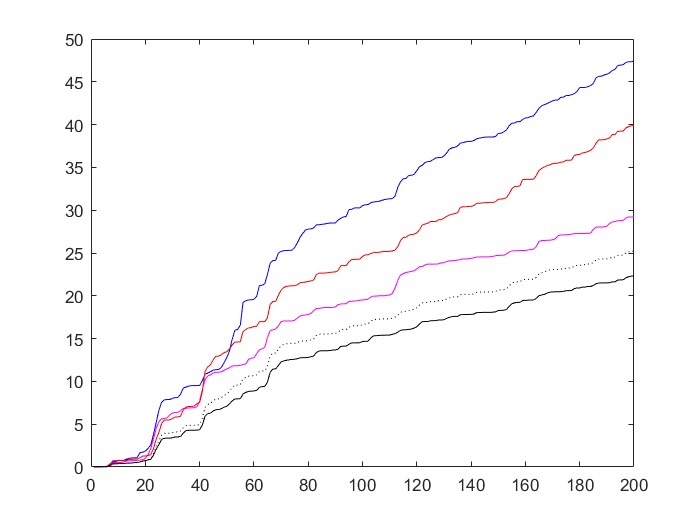
序列协方差交叉融合卡尔曼滤波器是一种高效处理多传感器多时滞系统中有色噪声和观测滞后问题的方法。通过协方差矩阵的交叉融合，能够显著提高状态估计的准确性，同时保持较高的实时性。尽管存在一些挑战，但该方法在无人机导航、智能机器人定位等场景中具有广泛的应用前景。

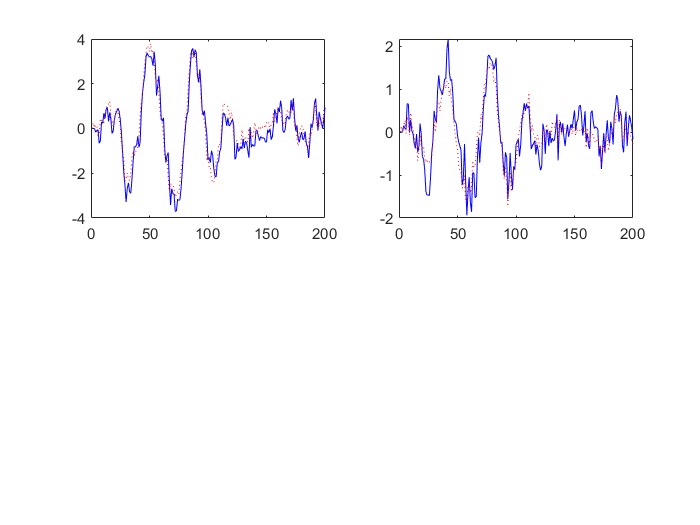
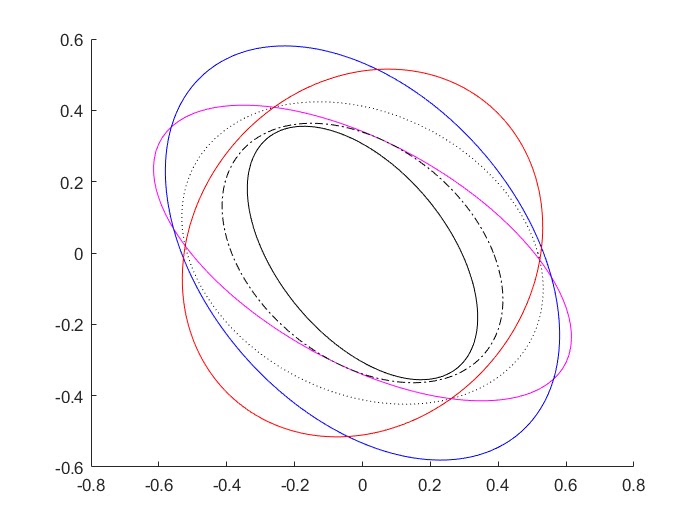
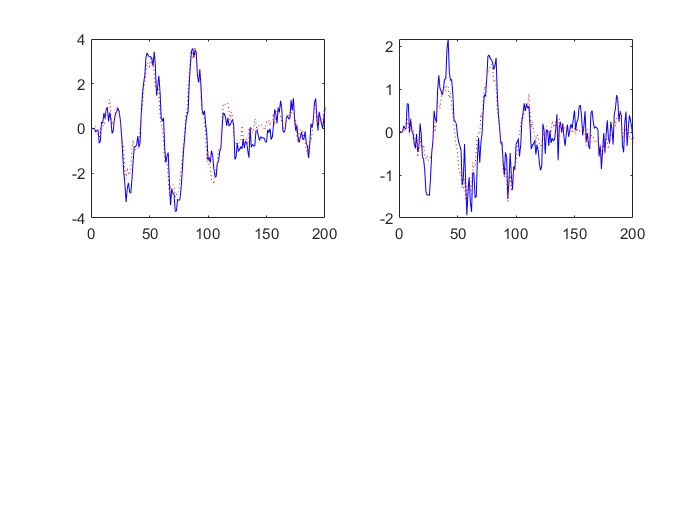
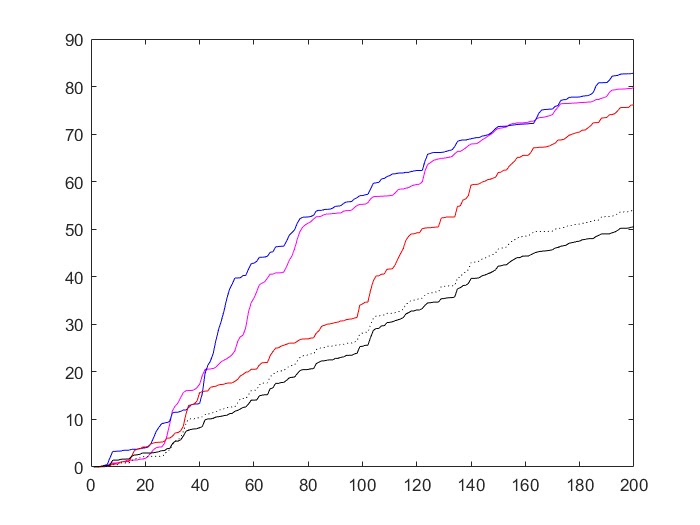
信息融合与状态估计 主要是针对多传感器多时滞（包括状态之后和观测滞后）系统，带有色噪声多重时滞传感网络系统的序列协方差交叉融合Kalman滤波器。 将带有色噪声的系统转化为带相关噪声的系统，然后再进行融合。