讲完了基础的线性代数之后，我们现在继续来学习高等数学在机器人中的应用。高等数学是机器人学的底层运算语言——它不像线性代数那样直接构造“空间与变换”，也不像概率论那样处理“不确定性与估计”，而是负责描述变化、积累、优化与动态。可以说，机器人能“动”、能“快”、能“准”，全靠高数在背后算。本章我们将从如下几个维度展开：

1、微分学：导数、梯度、雅可比矩阵在运动学、优化、控制中的应用。

2、积分学：路径积分、势场、动力学能量法。

3、微分方程：机器人动力学方程（ODE）、状态估计（微分方程）、轨迹跟踪控制。

4、向量分析：梯度、散度、旋度在人工势场、电磁场模拟中的应用。

5、级数：泰勒展开在系统线性化、优化算法中的应用。

6、多元函数极值：最优化问题，如路径规划、参数标定。

一、微分学

微分学其实就是我们高中阶段学习的导数，在高中学习的基础上我们再更深入的认识一下微分学吧。

1、极限

1.1 什么是极限

2、导数

2.1 导数的定义

函数 y=f(x)在点x0处的导数定义为：

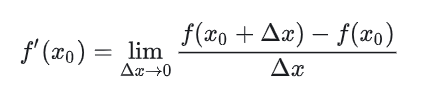
如果极限不存在，则称函数在x0处不可导。

几何意义：导数就是切线的斜率。

物理意义：导数就是瞬时变化率（如速度）。

2.2 可导与连续的关系

定理：可导必然连续，但连续不一定可导（例如 y=∣x∣在x=0处连续但不可导）。

2.3 导函数

3、基本初等函数的导数公式

4、求导法则

4.1 四则运算法则

4.2  复合函数求导

4.3 反函数求导法则

5、高阶导数

6、隐函数求导

7、参数方程求导

8、微分-----导数的线性近似

8.1 微分的定义

8.2 微分的运算法则

和导数完全对应：d(u±v)=du±dv，d(uv)=v du+udv，等等。

9、微分中值定理

9.1 罗尔定理

9.2 拉格朗日中值定理

9.3 柯西中值

10、洛必达法则-----解决0/0或∞/∞型极限

11、泰勒公式

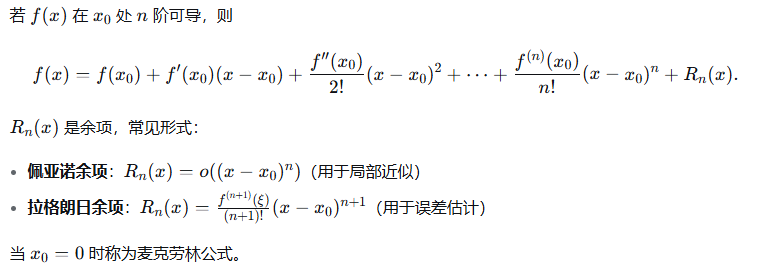
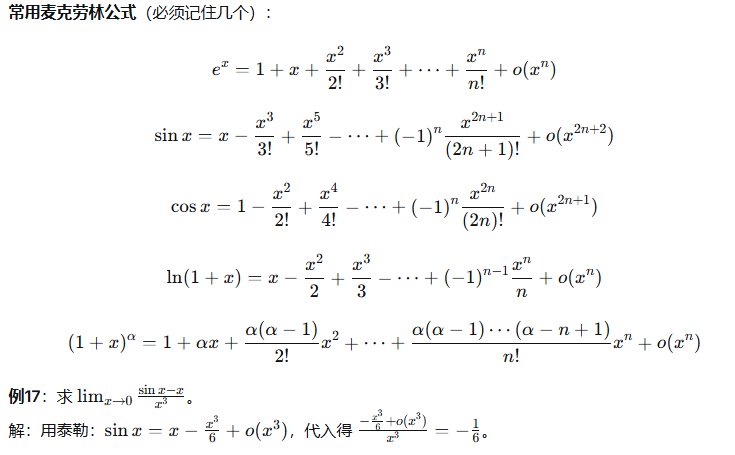
二、积分学

1、不定积分

1.1 原函数与不定积分

1.2 基本积分公式

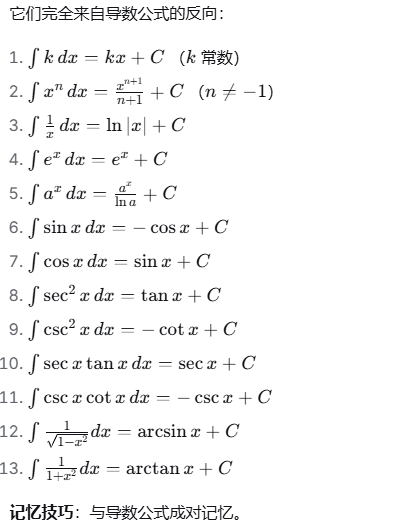
1.3 不定积分的线性性质

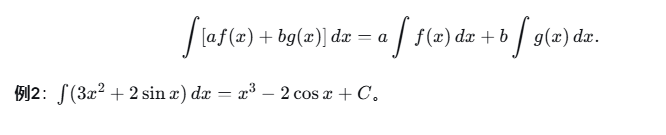
2、换元积分法-----复合函数的逆运算

2.1 第一类换元法（凑微分法）

2.2 变量代换法

3、分部积分法-----乘积的积分公式

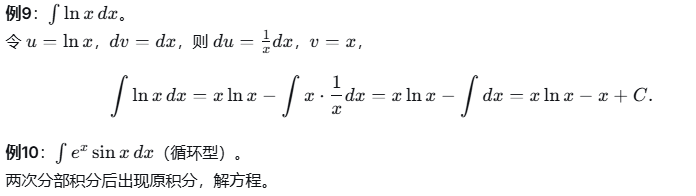
4、有理函数的积分-----部分分式法

5、定积分

5.1 从面积到定积分

5.2 牛顿-莱布尼茨公式

5.3 定积分的性质

5.4 定积分的换元法与分部积分法

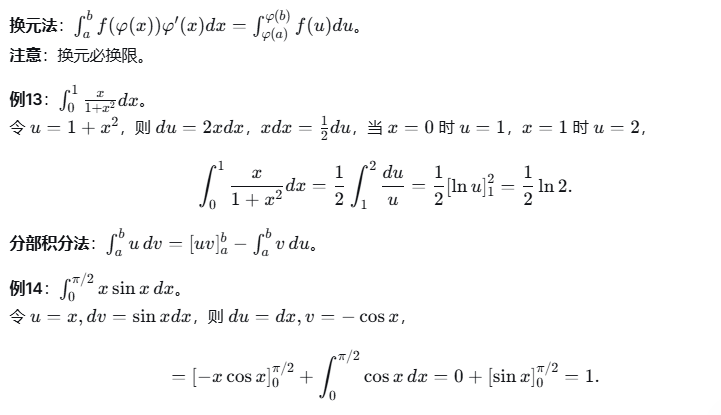
6、定积分的应用

6.1 平面图形的面积

6.2 旋转体的体积

6.3 平面曲线的弧长

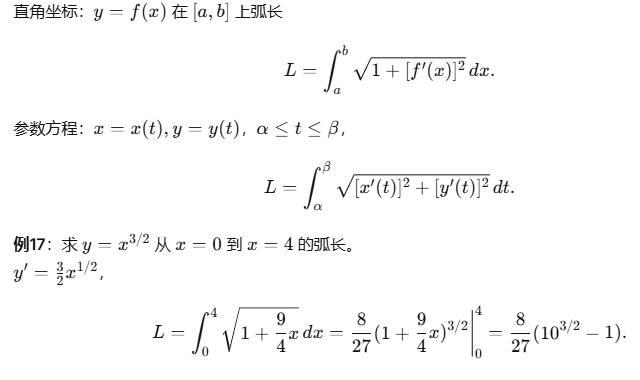
6.4 旋转曲面的面积

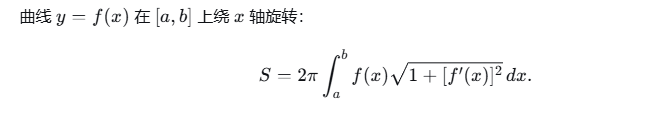
6.5 物理应用：变力做功、液体压力等

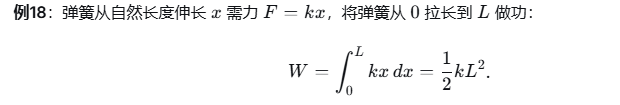
三、微分方程

1、微分方程的定义与基本术语

2、一阶微分方程解法大全

2.1 可分离变量方程

2.2 齐次方程

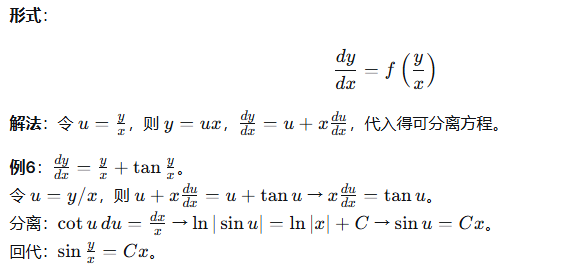
2.3 一阶线性微分方程

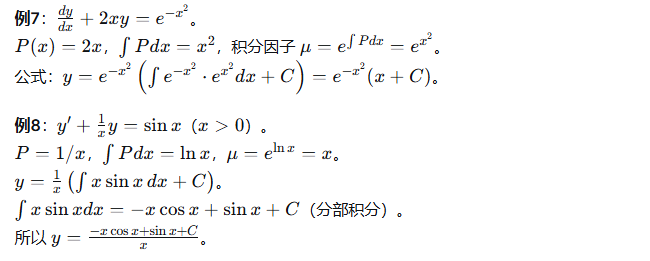
2.4 伯努利方程

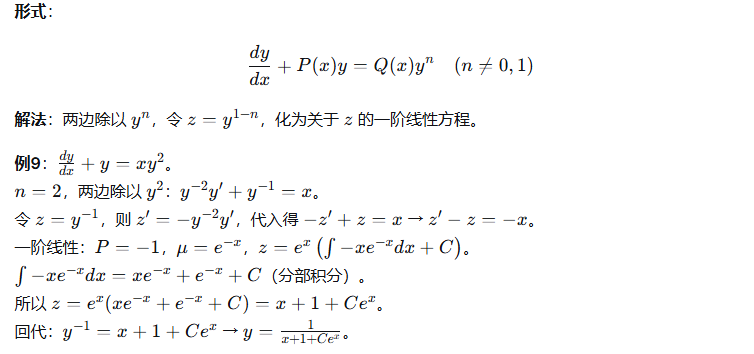
3、高阶线性微分方程

3.1 线性微分方程解的结构

3.2 常系数齐次线性微分方程

3.3 常系数非齐次线性微分方程——待定系数法

3.4 常数变易法（高阶线性非齐次）

3.5 欧拉方程

4、可降阶的高阶微分方程

4.1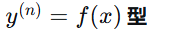 

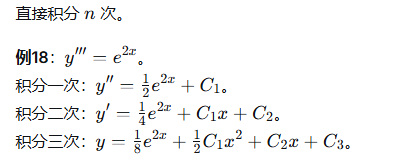
4.2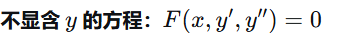 

4.3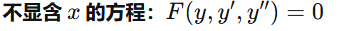 

5、微分方程的应用

5.1 几何应用

5.2 物理应用：运动学、动力学

四、向量分析

1、向量代数

1.1 向量的表示

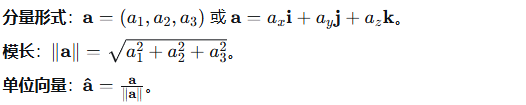
1.2 点积（数量积）

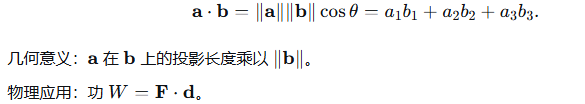
1.3 叉积（向量积）

2、向量函数与空间曲线

2.1 向量值函数

3、多元函数的微分学——梯度与方向导数

3.1 偏导数与全微分

3.2 梯度

3.3 方向导数

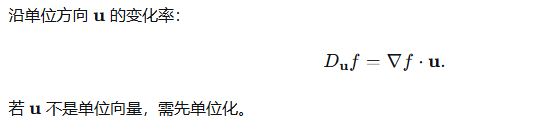
4、向量场

4.1 什么是向量场？

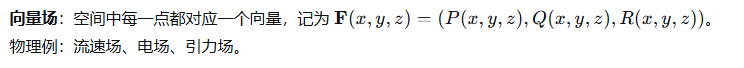
4.2 流线（场线）

5、线积分

线积分有两种：对标量场的积分（求曲线质量、弧长）和对向量场的积分（求功、环量）。

5.1 第一类线积分（对弧长）

5.2 第二类线积分（对坐标）

5.3 梯度场与保守场

6、格林定理 —— 平面上的“内积与外积”

7、曲面积分与通量

7.1 参数化曲面

7.2 第一类曲面积分（对标量场）

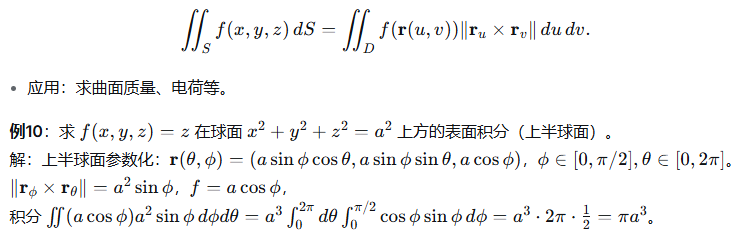
7.3 第二类曲面积分（对向量场，通量）

8、散度定理（高斯定理）

9、旋度与斯托克斯定理

9.1 旋度

9.2 斯托克斯定理

五、级数与逼近

1、常数项级数——无穷个数的和

1.1 级数的定义

1.2 收敛的必要条件

1.3 正项级数判别法

1.4 交错级数与绝对收敛

2、函数项级数与幂级数

2.1 函数项级数

2.2 幂级数

2.3 幂级数的性质

3、函数的幂级数展开——泰勒级数

3.1 泰勒公式与泰勒级数

3.2 常用函数的麦克劳林级数

3.3 利用幂级数求极限、近似计算

4、傅里叶级数——三角多项式逼近

4.1 周期函数的三角级数展开

4.2 收敛定理

4.3 正弦级数与余弦级数

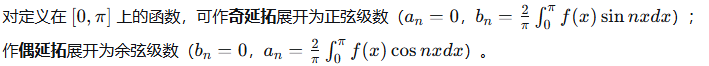
4.4 一般周期的傅里叶级数

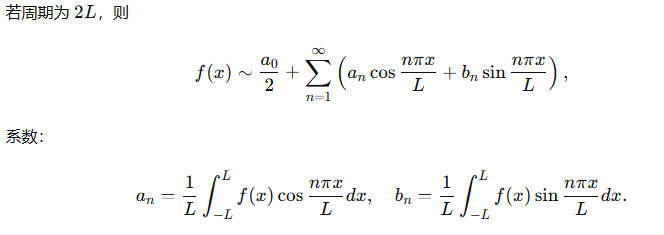
4.5 傅里叶级数的应用

5、逼近论初步

5.1 逼近问题

给定复杂函数 f(x)，我们希望用简单函数（多项式、三角多项式）在某种度量下近似它，且误差尽可能小。
这不仅是理论问题，也是数值计算、工程模拟的核心。

5.2 魏尔斯特拉斯逼近定理

5.3 最佳一致逼近——切比雪夫多项式

5.4 最佳平方逼近——傅里叶级数与正交多项式

5.5 实际应用场景

数值积分：将被积函数用多项式逼近再积分（高斯求积公式基于正交多项式）；

数值解微分方程：用多项式或三角多项式近似解（谱方法、有限元法）；

计算机辅助几何设计：贝塞尔曲线、B样条，本质上是多项式逼近；

深度学习：神经网络本质上也是函数逼近器，激活函数构造出庞大的函数空间。