【机器人路径规划】使用人工势场的移动机器人路径规划（Matlab实现）

人工势场法是移动机器人路径规划的一种常用方法，其原理基于势场法的思想，被视为最基础的方法。本文利用人工势场法原理对移动机器人的路径规划进行了研究，并通过仿真验证了其有效性。

荔枝科研社

511人浏览 · 2026-02-11 15:58:37

荔枝科研社 · 2026-02-11 15:58:37 发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

使用人工势场的移动机器人路径规划研究

摘要

引言

人工势场法原理

研究内容与方法

研究成果与结论

改进与优化

未来展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

人工势场法（Artificial Potential Field, APF）是一种常用的移动机器人路径规划方法。这种方法通过模拟物理中的势场理论来引导机器人的运动，从而实现从起始点到目标点的导航。使用人工势场的移动机器人路径规划，是通过在目标位置设置引力源产生引力，在障碍物周围设置斥力源产生斥力，机器人在引力与斥力共同作用下确定运动方向和速度。其优点包括实时性好、灵活性高、路径平滑；缺点有局部极小值问题、对环境变化敏感、参数调整困难。该方法在移动机器人导航等领域有广泛应用，且不断发展改进。

使用人工势场的移动机器人路径规划研究

摘要

引言

路径规划是移动机器人研究中的一个关键领域，主要目标是在有障碍物的环境中为机器人选择一条不碰障碍物的路径。路径规划分为全局路径规划和局部路径规划两部分。全局路径规划在环境信息比较全面的情况下进行，而局部路径规划则在环境信息部分了解的情况下进行。

人工势场法原理

人工势场法基于虚拟势场的概念，其中目标点产生引力场，障碍物产生斥力场。引力引导机器人走向目标点，而斥力帮助机器人避开障碍物。

引力场：
- 引力场的方向指向目标点。
- 引力的大小与机器人离目标点的距离有关，通常与距离的平方成反比。
斥力场：
- 斥力场的方向指向远离障碍物的方向。
- 斥力的大小与机器人离障碍物的距离有关，当距离较小时斥力较大，当距离超过一定范围时斥力为零。

研究内容与方法

本文通过使用MATLAB进行仿真，验证了人工势场法在移动机器人路径规划中的有效性。研究内容包括对势场分布的计算、引力场和斥力场的设定以及路径规划的算法实现。

环境建模：
- 对机器人的工作环境进行建模，包括目标点、障碍物和机器人的初始位置。
算法实现：
- 根据人工势场法的原理，实现引力场和斥力场的计算。
- 根据势场分布，为机器人规划出一条从起始点到目标点的路径。
仿真验证：
- 通过MATLAB进行仿真，验证所规划路径的有效性。
- 评估路径的安全性、效率以及算法的收敛速度。

研究成果与结论

研究结果表明，人工势场法可以有效地为移动机器人规划出一条安全的路径。通过调整引力场和斥力场的参数，可以优化路径的效率和安全性。

优点：
- 路径规划算法简单直观，易于实现。
- 在障碍物较少的环境下，路径规划效果良好。
缺点：
- 在障碍物密集或复杂的环境下，可能存在局部最优解问题。
- 斥力场和引力场的参数调整需要一定的经验。

改进与优化

针对人工势场法存在的问题，本文提出了一些改进和优化方法，如引入中间目标点来避免局部最优解，以及通过调整斥力场函数来确保目标点为全局最小点。

引入中间目标点：
- 在检测到局部最优解时，设置中间目标点，使机器人能够跳出局部最优解，继续向目标点前进。
调整斥力场函数：
- 通过分析斥力函数，将机器人和目标的相对距离考虑进去，建立新的斥力场函数，确保目标点为整个势场的全局最小点。

未来展望

随着人工智能和机器学习技术的发展，未来可以进一步探索将深度学习等人工智能技术应用于人工势场法中，以提高路径规划的准确性和效率。此外，多传感器融合技术也可以用于提高机器人的环境感知能力和定位精度，从而进一步提升路径规划的性能。

📚2 运行结果

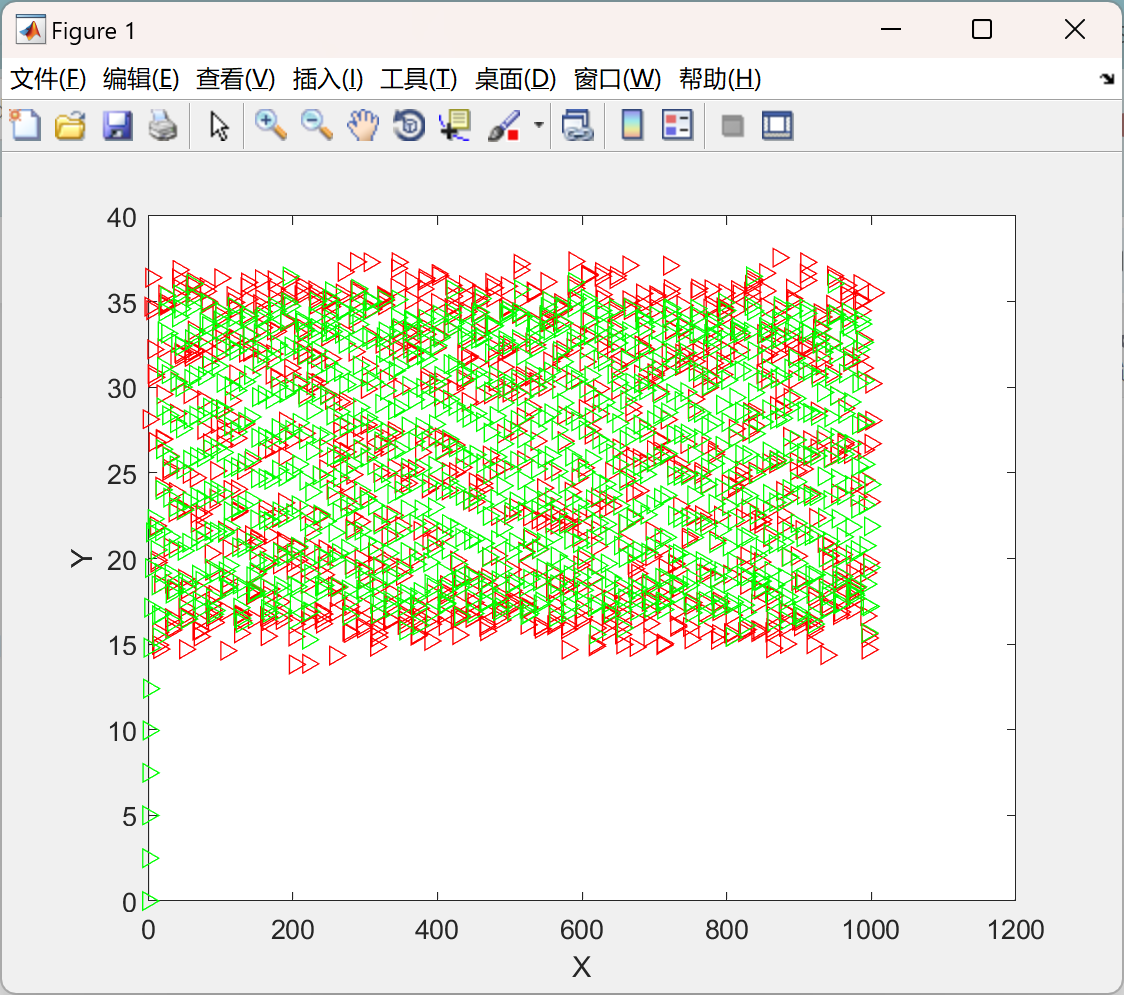
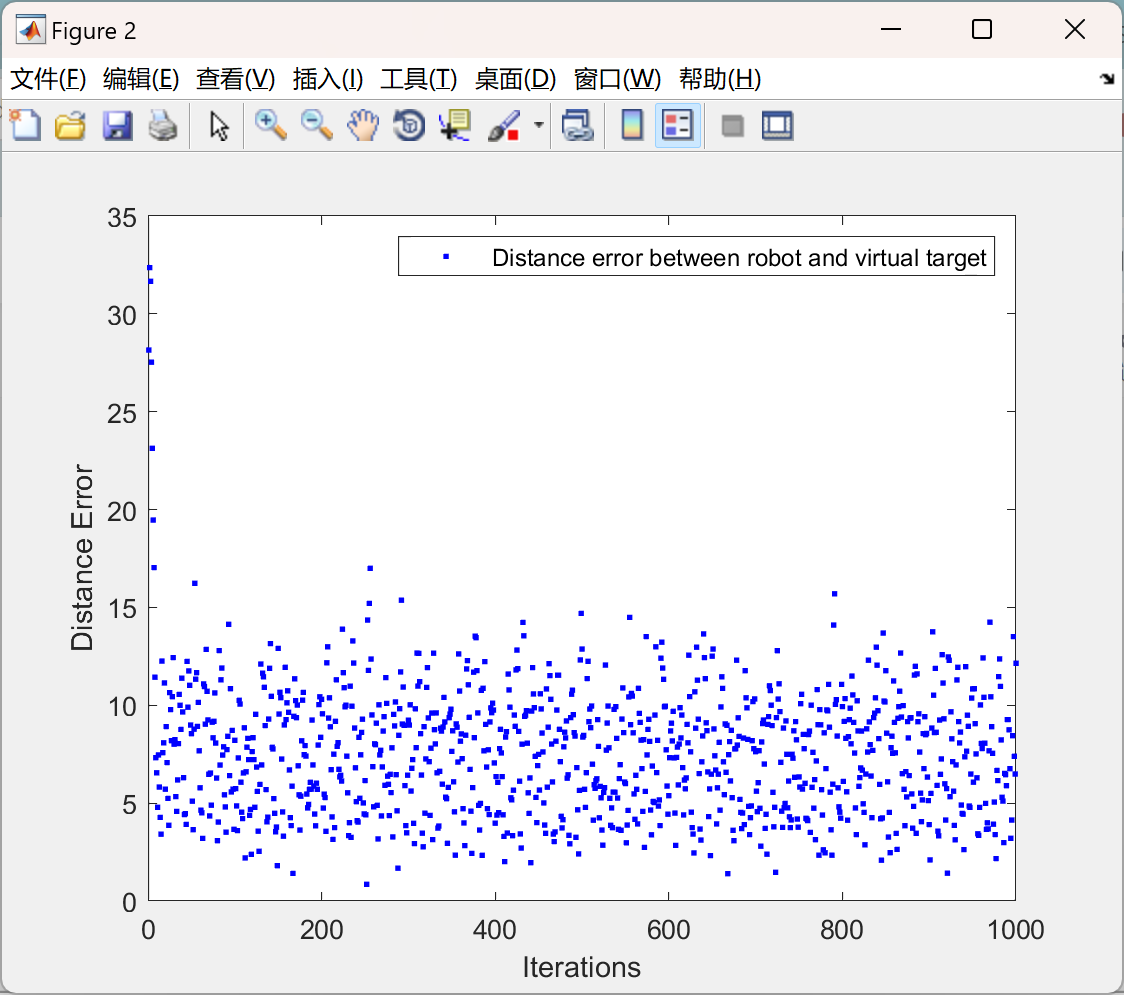
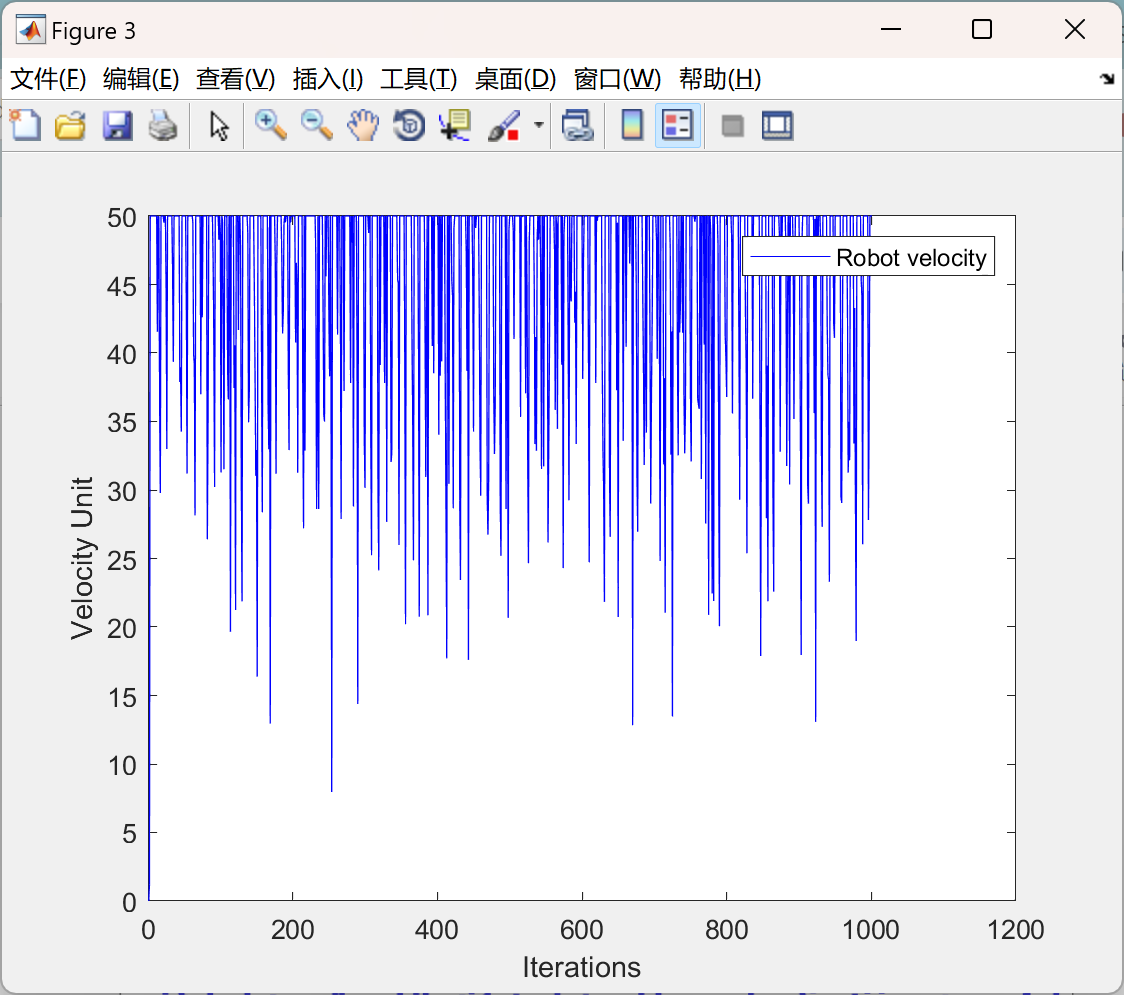
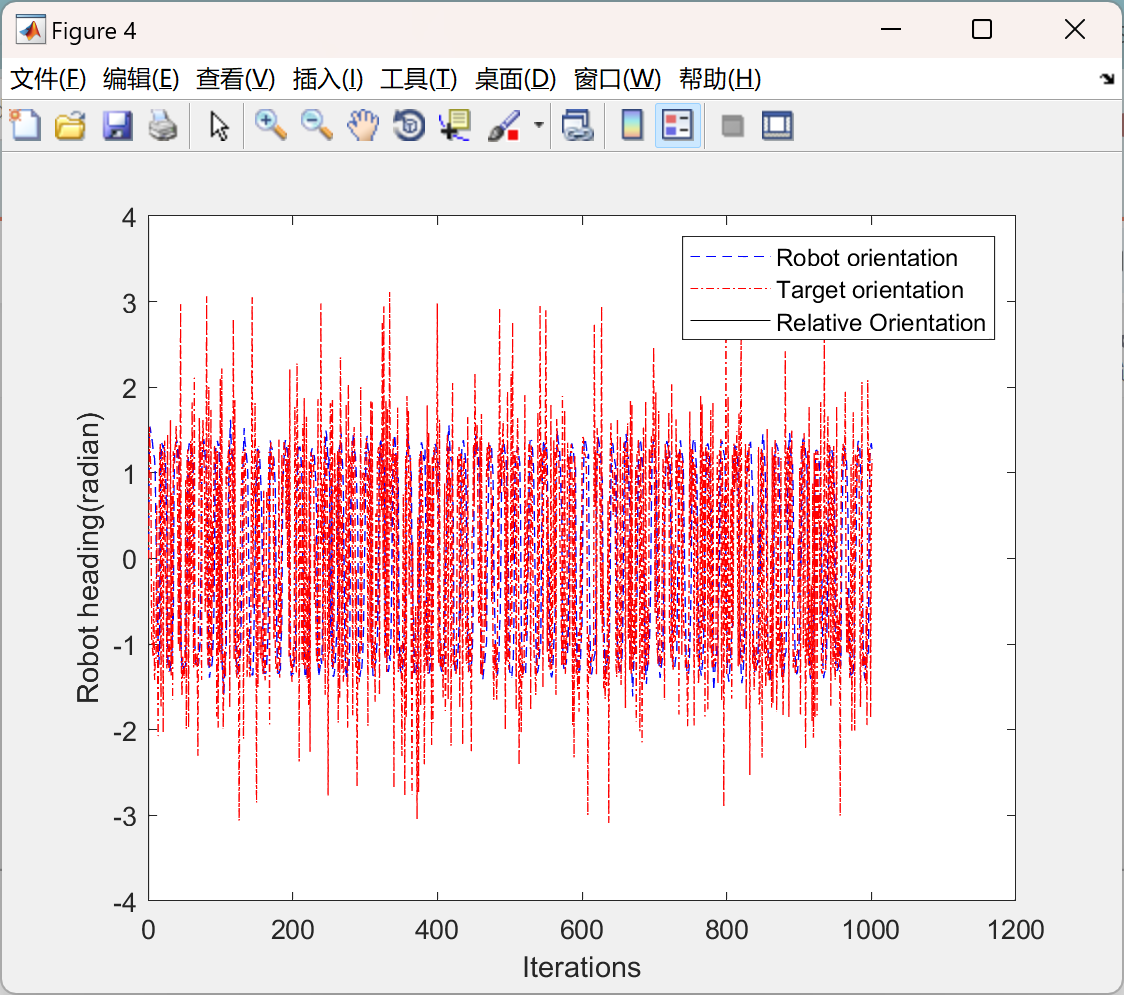
主函数部分代码:

clc,clear
close all
n = 2; % Number of dimensions
delta_t = 0.05; % Set time step
t = 0:delta_t:50;% Set total simulation time 0 0.05 0.1 0.15.....
lambda = 8.5; % Set scaling factor of attractive potential field
vr_max = 50; % Set maximum of robot velocity

%Set Virtual Target
qv = zeros (length(t),n); %Initial positions of virtual target 
pv = 1.2; %Set velocity of virtual target
theta_t = zeros (length(t),1); % Initial heading of the virtual target

%Set Robot
qr = zeros (length(t),n); %initial position of robot
vrd =  zeros (length(t),1); %Initial velocity of robot
theta_r = zeros (length(t),1); % Initial heading of the robot


qrv = zeros (length(t),n); %Save relative positions between robot and virtual target
prv = zeros(length(t),n); %Save relative velocities between robot and virtual target

qrv(1,:) = qv(1,:) - qr(1,:);%Compute the initial relative position

%Compute the initial relative velocity
prv(1,:) = [pv*cos(theta_t(1))-vrd(1)*cos(theta_r(1)), pv*sin(theta_t(1))-vrd(1)*sin(theta_r(1))];

%====Set noise mean and standard deviation====
noise_mean = 0.8;
noise_std = 0.8;

pause('on')

for i =2:length(t)  
    %++++++++++CIRCULAR TRAJECTORY+++++++++++
      %Set target trajectory moving in CIRCULAR trajectory WITHOUT noise
%     qv_x = 60 - 15*cos(t(i));
%     qv_y = 30 + 15*sin(t(i));
%     qv(i,:) = [qv_x, qv_y]; %compute position of virtual target
     
     %Set target trajectory moving in CIRCULAR trajectory WITH noise
%    qv_x = 60 - 15*cos(t(i))+ noise_std * randn + noise_mean;
%    qv_y = 30 + 15*sin(t(i)) + noise_std * randn + noise_mean;
%    qv(i,:) = [qv_x, qv_y];  %compute position of target

    %++++++++++LINEAR TRAJECTORY+++++++++++
      %Set target trajectory moving in Linear trajectory WITHOUT noise
%     qv_x = t(i);
%     qv_y = qv_x + 100;
%     qv(i,:) = [qv_x, qv_y]; %compute position of virtual target
     
     %Set target trajectory moving in Linear trajectory WITH noise
%    qv_x = i + noise_std * randn + noise_mean;
%    qv_y = qv_x + 100 + noise_std * randn + noise_mean;
%    qv(i,:) = [qv_x, qv_y];  %compute position of target

        %++++++++++SINE WAVE TRAJECTORY+++++++++++
      %Set target trajectory moving in sine trajectory WITHOUT noise
%    qv_x = i;
%    qv_y = 10*sin(1/3*qv_x) + 25;
%    qv(i,:) = [qv_x, qv_y]; %compute position of virtual target
     
     %Set target trajectory moving in sine trajectory WITH noise
    qv_x = i + noise_std * randn + noise_mean;
    qv_y = 10*sin(1/3*qv_x) + 25 + noise_std * randn + noise_mean;
    qv(i,:) = [qv_x, qv_y];  %compute position of target
    
    
    
    %Compute the target heading
    qt_diff(i,:) =qv(i,:)- qv(i-1,:);
    theta_t(i) = atan2(qt_diff(i,2),qt_diff(i,1)); 
    
    %Calculation
    phi=atan2(qrv(i-1,2),qrv(i-1,1));
    
    vrd(i) = sqrt((norm(pv)^2) + 2*lambda*norm(qrv(i-1,:))*abs(cos(theta_t(i)- phi)) + (lambda^2)*(norm(qrv(i-1,:))^2));
    
    if vrd(i)>vr_max
        vrd(i)= vr_max;
    end
    
    theta_r(i) = phi + asin((norm(pv)*sin(theta_t(i) - phi))/(vrd(i)));