雅可比矩阵（Jacobian Matrix）-- 自学小结

雅可比矩阵是向量值函数的一阶偏导数矩阵，在优化理论、机器学习、机器人学等领域有广泛应用。其几何意义在于描述某点附近的局部线性变化关系。在机器人学中，雅可比矩阵是关节空间速度向末端操作空间速度传递的映射矩阵，反映关节与末端执行器的瞬时运动关系。求解方法包括位置求导法和矢量积法。此外，雅可比矩阵还可用于力和力矩的映射，速度雅可比矩阵的转置即为力雅可比矩阵。该矩阵体现了末端操作力与关节力矩之间的转换关系

编程的小鱼塘

425人浏览 · 2026-02-10 16:36:36

编程的小鱼塘 · 2026-02-10 16:36:36 发布

雅可比矩阵（Jacobian Matrix）是向量值函数的一阶偏导数矩阵。其从形式上来看，就是函数的偏导数所构成的矩阵形式，在现代的科学与工程之中，雅可比矩阵有着广泛的应用，包括优化理论、机器学习、机器人学、计算机视觉等理论。雅可比矩阵发挥着至关重要的作用。

简单来说雅可比矩阵的几何意义，就是对于直角坐标系中的某点进行函数的变化关系，但在某点的附近仍然满足的是局部的线性变化关系，近似看成线性变化关系。用公式简单描述就是：

所以从这个公式也可以比较明显的看出来其实在某点比较小的范围内可以近似看成一种线性的变化关系。

从上面的图中看出来其实也就相当于进行两次的函数变化，坐标系的不一定的非线性变化，此时我们分别对这两个过程进行分析，对其的原x和y方向分别两步分析，近似成线性的变化，所以分别对其两个变量求偏导，得到第一列为两次函数变化对x轴方向的变化分析，第二列为对y轴方向的变化分析。

了解了雅可比矩阵的具体几何意义之后，该如何应用雅可比矩阵来处理问题呢？

首先我们肯定要确定函数的输入和输出的变量分别是什么，其实输入简单来说就是独立的因变量，输出是依赖变量，被控量，由x唯一确定的输出。矩阵的行数是输出变量的个数，列数是输入变量的个数。下面举几个比较常见的例子解释一下：

坐标系变换 原坐标系变量为输入（x、y）；新坐标系作为输出（r、 $\theta$ ）
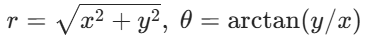
机器人学 关节空间变量为输入（关节角/位移）；笛卡尔空间位姿（末端xyz/姿态角）或者已知关节速度，可求末端的速度映射

确定输入和输出之后，我们就可以对输出分量计算各个输入变量的偏导数，然后组成雅可比矩阵的形式即可。

下面重点写一下在机器人学里面的雅可比矩阵的应用：

在机器人学中，雅可比矩阵（Jacobian Matrix）其实是关节空间速度向末端操作空间速度传递的映射矩阵，本质是描述关节与末端执行器瞬时运动关系的映射，因此雅可比矩阵是与时间相关的。其实就是任意的关节变化 $\Delta Q$ 与末端 $\Delta X$ 的关系，这个 $\Delta$ 代表了瞬时运动的一个微小量，也可以理解为微分运动。

求解雅可比矩阵有位置求导法、矢量积法、微分变换法和速度递推法。下面重点聊一聊前两种方法，在聊之前先了解几个概念：什么是关节空间、关节空间速度、操作空间、操作空间速度？

关节空间：由各个关节角度或位移构成的向量，这里统一用q来表示关节变量，所以n维关节空间为： $q=\left [ q_1,q_2,\cdots ,q_n \right ]^{T}$ 。其中指的就是转角的大小和位移的距离。

操作空间：末端的位姿状态（末端坐标，角度）构成的向量，m维操作空间记为： $X=\left [ x_1,x_2,\cdots ,x_m \right ]^{T}$ 。此时其中描述的是位置变量。

操作空间速度：描述末端执行器在笛卡尔空间中的运动速率，是一个6维空间速度向量

一、位置求导法

对于关节空间和操作空间而言，这里的每一个位姿状态 $x_i$ 都同时由n个关节来共同决定，所以满足一定函数关系： $x_i=f_i\left ( q_1,q_2,\cdots q_n \right )$ ，所以这时其实就可求操作空间速度，由x与q的函数关系，两边对时间求偏导即可表示操作空间的速度。

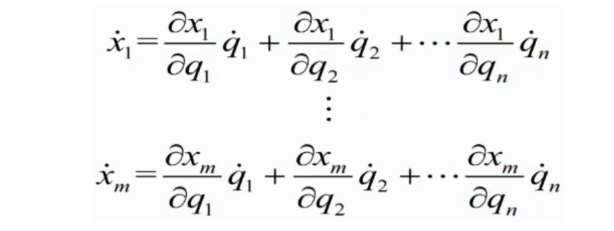
所以很容易就可知其中的雅可比矩阵的格式，也就是操作空间参数对于各个关节变量的参数的偏导数。下面举一个具体的实例来说明一下，在二维的平面里可知：

二、矢量积法

简而言之这个方法就是将机器人各关节在末端产生的速度进行叠加，进而得到操作空间的速度。为了简单理解，举个类似上面的小例子，可以体会其中的方法：

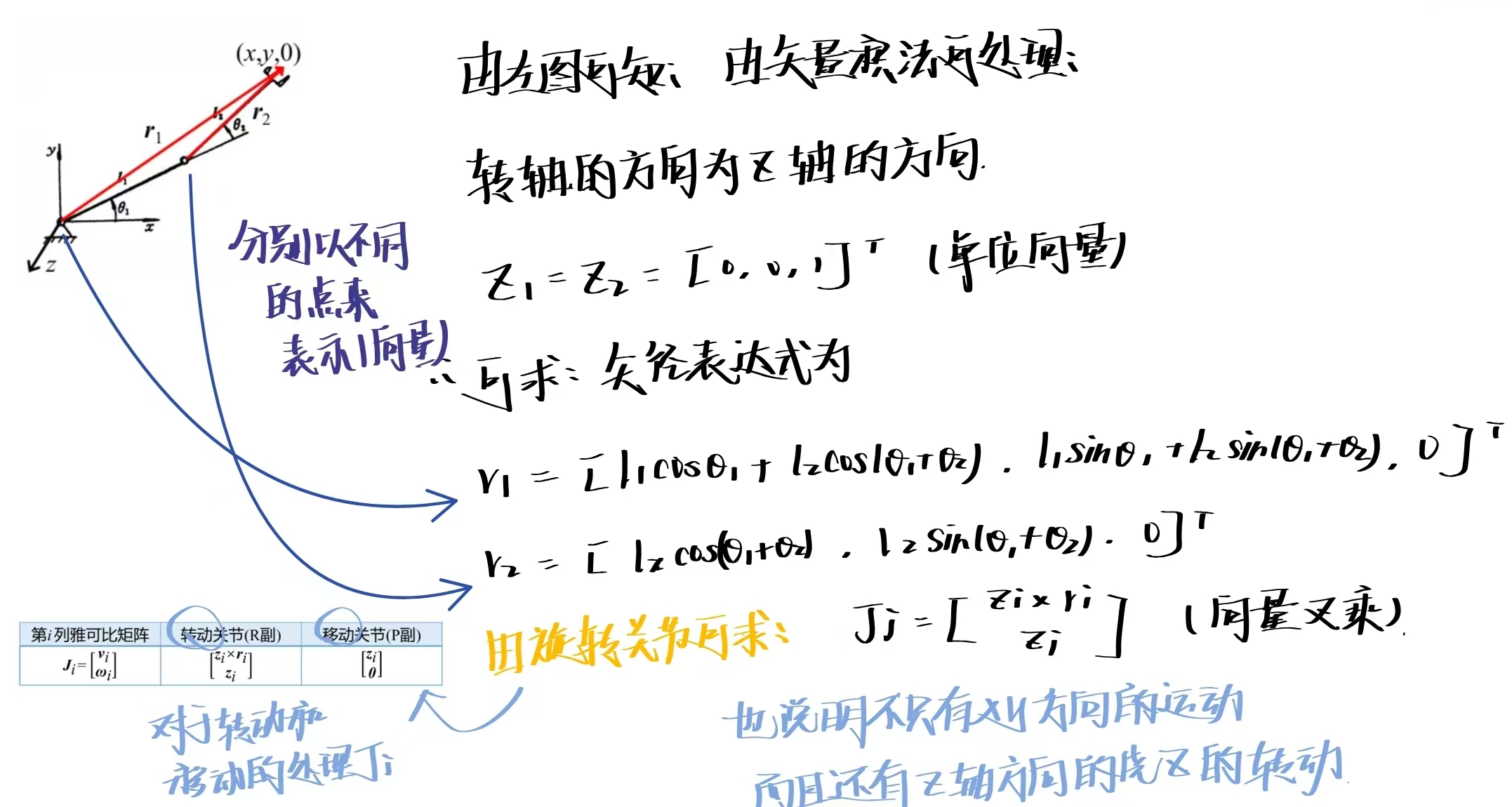
所以从上面的图其实就可以比较明显的看出来其中的矢量积法的应用，找对应的矢量表示，同时找到对应的旋转轴z轴，其中的z轴一般是要与xy轴相互垂直的关系。然后根据上图给的表格即可找到对应的转动/移动的雅可比公式即可表示雅可比矩阵。

其实雅可比矩阵还可以实现在力和力矩之间的应用，雅克比矩阵还可以体现末端执行器上施加的力和关节上施加的力矩之间的关系。也就是已知末端的载荷，静止状态下的各关节驱动力矩的大小，这个映射关系也可为静力雅可比矩阵。目前只了解到其中其实是虚功原理的应用，对于虚功原理定义如下：理想约束下，系统保持静止的条件：所有作用于该系统的主动力对质点系的虚位移所作的功的和为零。

但最终的结论可以了解一下，速度雅可比矩阵和力矩的雅可比矩阵其实之间有着相互联系

速度雅可比矩阵转置之后可以得到力的雅可比矩阵。

最后大家可以思考一句话：力雅可比矩阵是m维操作空间向n维关节空间的映射，因此关节力矩总是由末端操作力唯一确定。然而对于给定的关节力矩，与之平衡的末端操作力不一定存在。这句话的意义其实可以类比一下我们要推一个箱子，就好比在推箱子时，你知道各关节受多少力；并且这个各个关节的受力也是唯一确定的，但当关节受力异常时，你无法确定是外面推的力还是里面卡住了的原因，所以操作力就不一定存在。