三维RRT路径规划算法。 RRT、RRT*和双向RRT。 输出时间和路径长度，三种路径规划算法基于matlab

在机器人运动规划领域，路径规划算法一直是研究的热点。今天咱们就来深入聊聊三维空间中的RRT（快速扩展随机搜索，Rapidly - exploring Random Tree）路径规划算法家族，包括RRT、RRT*以及双向RRT，并通过Matlab实现它们，同时输出时间和路径长度。

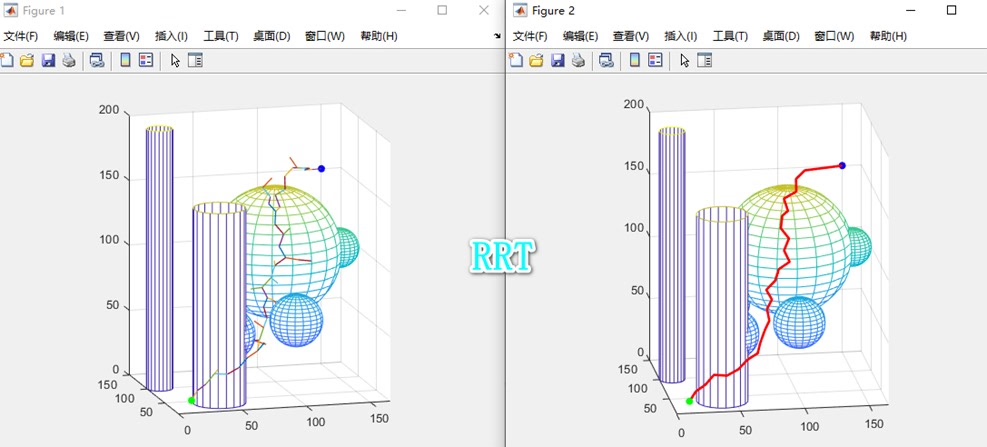
RRT算法基础

RRT算法的核心思想是通过在搜索空间中随机采样点，不断扩展树状结构来寻找从起点到目标点的路径。下面是一段简单的Matlab伪代码示意其基础流程：

% 初始化树，根节点为起点
tree = [start_point];
while ~found_path
    % 随机采样一个点
    sample = random_sample(); 
    % 找到树中距离采样点最近的节点
    nearest = nearest_neighbor(tree, sample); 
    % 尝试从最近节点向采样点扩展
    new_node = extend(nearest, sample); 
    if collision_free(new_node)
        % 将新节点加入树中
        tree = [tree; new_node]; 
        if near_goal(new_node)
            % 找到了目标点，生成路径
            path = generate_path(tree, start_point, goal_point); 
            found_path = true;
        end
    end
end

代码分析

1. 初始化树：从起点开始构建树结构，这是整个搜索的起始点。
2. 随机采样：random_sample()函数在整个搜索空间中随机生成一个点，这使得算法能有效探索不同区域。
3. 寻找最近节点：nearest_neighbor()通过计算距离，在已有树节点中找到距离采样点最近的，这一步引导树向采样点方向扩展。
4. 扩展节点：extend()函数尝试从最近节点向采样点移动一定步长，生成新节点。
5. 碰撞检测：collision_free()判断新节点是否与障碍物碰撞，只有无碰撞时才加入树。
6. 目标判断：near_goal()检查新节点是否接近目标点，若接近则生成路径。

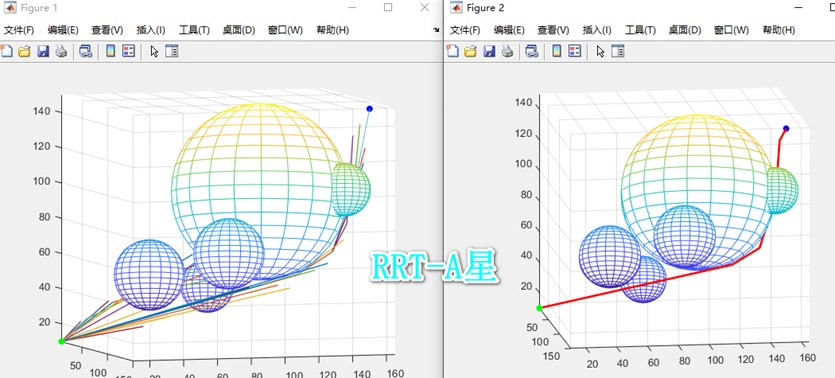
RRT*算法改进

RRT是对RRT的优化，它在扩展树的同时进行重布线（rewiring）操作，使树的结构更优，找到更短路径。以下是RRT相对RRT新增操作的Matlab代码示意：

% 在扩展新节点后
if collision_free(new_node)
    tree = [tree; new_node]; 
    % 重布线操作
    for i = 1:size(tree, 1)
        if collision_free(tree(i, :), new_node) && cost(tree(i, :)) + distance(tree(i, :), new_node) < cost(new_node)
            new_parent = i;
            new_node = [new_node; new_parent];
            % 更新新节点到起点的代价
            cost(new_node) = cost(tree(i, :)) + distance(tree(i, :), new_node); 
        end
    end
    if near_goal(new_node)
        path = generate_path(tree, start_point, goal_point); 
        found_path = true;
    end
end

代码分析

1. 重布线循环：遍历树中所有节点，检查是否可以通过新节点重新连接，以降低到起点的代价。
2. 条件判断：既要保证新连接无碰撞，又要确保新连接路径代价小于当前新节点到起点的代价。
3. 更新节点：若满足条件，更新新节点的父节点和代价，优化树结构。

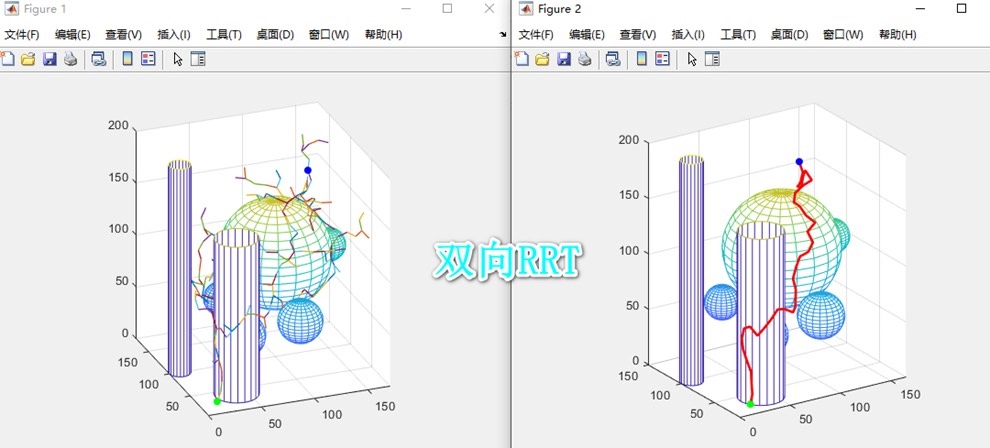
双向RRT算法

双向RRT同时从起点和目标点开始构建两棵树，分别向对方扩展，期望更快相遇。Matlab代码大致如下：

% 初始化两棵树，分别从起点和目标点开始
tree_start = [start_point];
tree_goal = [goal_point];
while ~trees_connected
    % 随机采样
    sample = random_sample(); 
    % 从起点树扩展
    nearest_start = nearest_neighbor(tree_start, sample); 
    new_node_start = extend(nearest_start, sample); 
    if collision_free(new_node_start)
        tree_start = [tree_start; new_node_start]; 
        % 检查是否与目标树连接
        if near_tree(tree_goal, new_node_start)
            path = connect_trees(tree_start, tree_goal, new_node_start); 
            trees_connected = true;
        end
    end
    % 从目标树扩展（类似起点树扩展操作）
    nearest_goal = nearest_neighbor(tree_goal, sample); 
    new_node_goal = extend(nearest_goal, sample); 
    if collision_free(new_node_goal)
        tree_goal = [tree_goal; new_node_goal]; 
        if near_tree(tree_start, new_node_goal)
            path = connect_trees(tree_start, tree_goal, new_node_goal); 
            trees_connected = true;
        end
    end
end

代码分析

1. 双树初始化：分别以起点和目标点为根构建两棵树。
2. 交替扩展：每次循环从起点树和目标树交替扩展，随机采样点用于引导扩展方向。
3. 连接检测：每次扩展新节点后，检查新节点是否接近另一棵树，若接近则连接两棵树生成路径。

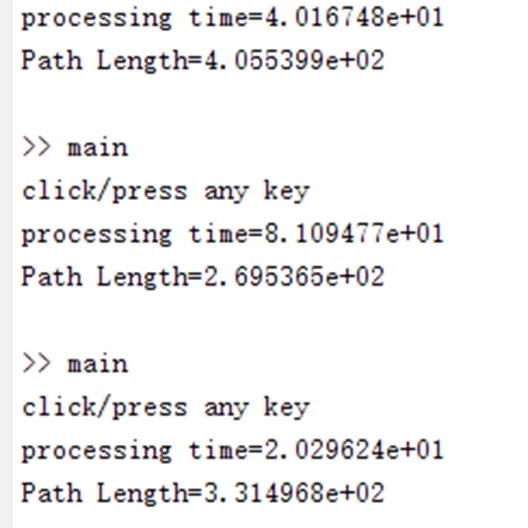
输出时间和路径长度

在Matlab实现中，为了输出每种算法的运行时间和路径长度，可以使用如下代码：

% 记录开始时间
start_time = tic; 
% 运行路径规划算法（以RRT为例）
path = rrt(start_point, goal_point, obstacles); 
% 记录结束时间
end_time = toc(start_time); 
% 计算路径长度
path_length = 0;
for i = 1:length(path)-1
    path_length = path_length + distance(path(i, :), path(i + 1, :));
end
fprintf('RRT算法运行时间: %f 秒\n', end_time);
fprintf('RRT算法路径长度: %f\n', path_length);

代码分析

1. 时间记录：tic和toc函数分别用于记录算法开始和结束时间，从而得到运行时间。
2. 路径长度计算：通过循环累加路径中相邻节点的距离，得到路径总长度。

总结一下，RRT、RRT和双向RRT在三维路径规划中各有特点。RRT简单易实现，RRT能找到更优路径，双向RRT则在搜索效率上有优势。通过Matlab实现并分析它们的运行时间和路径长度，可以根据实际需求选择最合适的算法。希望这篇博文能帮助大家更好地理解和应用三维RRT路径规划算法家族。

三维RRT路径规划算法。 RRT、RRT*和双向RRT。 输出时间和路径长度，三种路径规划算法基于matlab