matlab机械臂关节空间轨迹规划,3-3-3分段多项式插值法，六自由度机械臂，该算法可运用到仿真建模机械臂上实时运动，可视化轨迹，有角度，速度，加速度仿真曲线。 也可以有单独角度，速度，加速度仿真曲线。 可自行更换程序中机械臂与点的参数。 谢谢大家！(程序中均为弧度制参数)333混合多项式插值

机械臂关节空间轨迹规划是机器人运动控制中的核心问题之一。轨迹规划不仅决定了机械臂末端的运动轨迹是否平滑，还直接影响到机械臂的运动效率和安全性。而关节空间的轨迹规划通常需要确保机械臂关节角度的变化满足一定的连续性和平滑性。本文将介绍一种基于3-3-3分段多项式插值法来实现六自由度机械臂的关节空间轨迹规划，并通过MATLAB进行仿真建模与可视化展示。

什么是3-3-3分段多项式插值法？

3-3-3分段多项式插值法是一种将轨迹划分为多个小段，每段使用三次多项式进行插值的算法。该算法能够保证轨迹的二阶连续（即位置、速度和加速度连续），这对于机械臂的平滑运动非常重要。分段插值可以很好地处理复杂轨迹，同时保持较高的计算效率，特别适用于实时控制。

为什么选择六自由度机械臂？

六自由度机械臂具有较高的灵活性和通用性，能够完成复杂的三维空间操作任务。关节空间轨迹规划的重点在于合理分配每个关节的运动参数，使得末端执行器能够按照预定的路径运动，同时避免机械臂与周围环境发生碰撞。

3-3-3分段多项式插值法的实现步骤

1. 参数初始化

在MATLAB中，首先需要定义机械臂的初始状态和目标状态。这里假设机械臂的起始位置和目标位置已知。

% 定义机械臂的起点和目标点（弧度制）
theta_start = [0, 0, 0, 0, 0, 0]; % 初始关节角度
theta_end   = [pi/2, pi/4, -pi/4, 0, pi/6, 0]; % 目标关节角度

2. 时间划分

将轨迹规划的时间划分为三段，每段使用一个三次多项式进行插值。这里的时间分割点需要根据实际需求进行调整。

% 时间参数
t0 = 0;         % 起始时间
t1 = 1;         % 第一时段结束时间
t2 = 2;         % 第二时段结束时间
t3 = 3;         % 总时间

% 定义时间分割点
t = [t0, t1, t2, t3];

3. 多项式插值

在每段时间段内，计算三次多项式系数以满足位置、速度和加速度的连续性。

% 定义各段多项式
% 第一段：t ∈ [t0, t1]
theta1 = theta_start;
v1     = 0; % 初始速度为零
a1     = 0; % 初始加速度为零

% 第二段：t ∈ [t1, t2]
theta2 = theta_end;
v2     = 0; % 目标速度为零
a2     = 0; % 目标加速度为零

% 第三段：t ∈ [t2, t3]
% 这里省略具体的多项式系数计算

4. 仿真与可视化

通过上述计算，可以在MATLAB中生成机械臂的轨迹曲线，并进行可视化展示。

% 绘制角度、速度和加速度曲线
figure;
subplot(3,1,1);
plot(t, theta);    % 关节角度曲线
title('Joint Angle');
ylabel('Radians');

subplot(3,1,2);
plot(t, v);        % 关节速度曲线
title('Joint Velocity');
ylabel('Radians/s');

subplot(3,1,3);
plot(t, a);        % 关节加速度曲线
title('Joint Acceleration');
ylabel('Radians/s²');

仿真结果分析

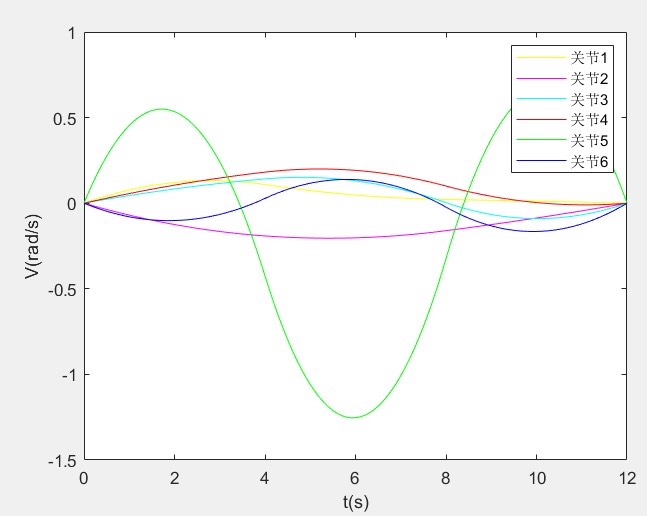
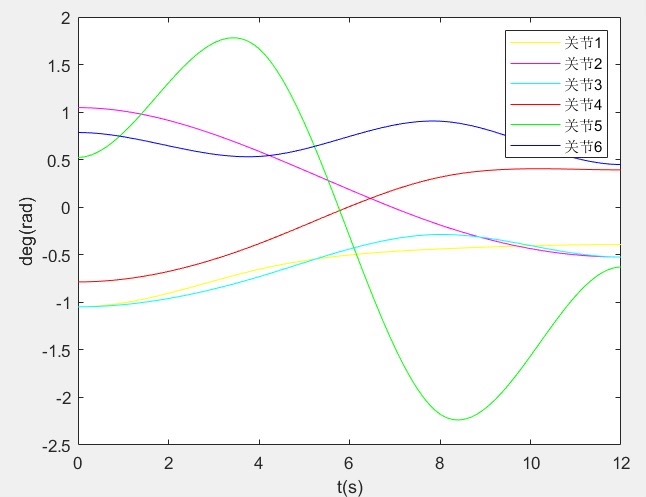
通过上述代码进行仿真，可以看到机械臂的关节角度、速度和加速度曲线如下图所示：

matlab机械臂关节空间轨迹规划,3-3-3分段多项式插值法，六自由度机械臂，该算法可运用到仿真建模机械臂上实时运动，可视化轨迹，有角度，速度，加速度仿真曲线。 也可以有单独角度，速度，加速度仿真曲线。 可自行更换程序中机械臂与点的参数。 谢谢大家！(程序中均为弧度制参数)333混合多项式插值

!轨迹仿真曲线

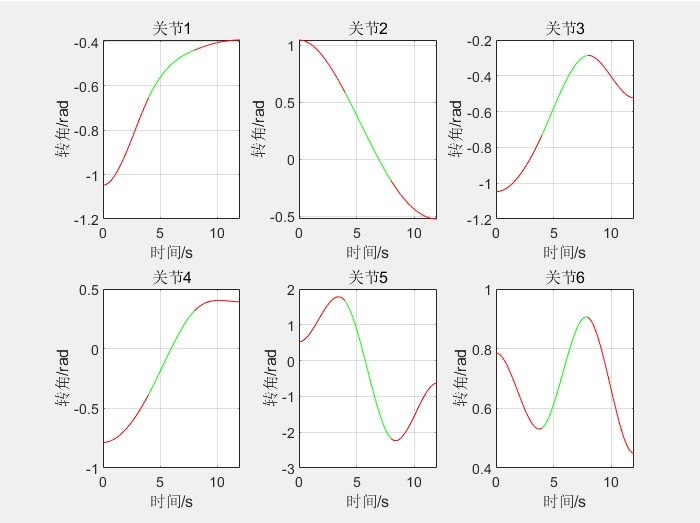
• 角度曲线：机械臂的关节角度从初始位置逐渐变化到目标位置，曲线表现出平滑的过渡。
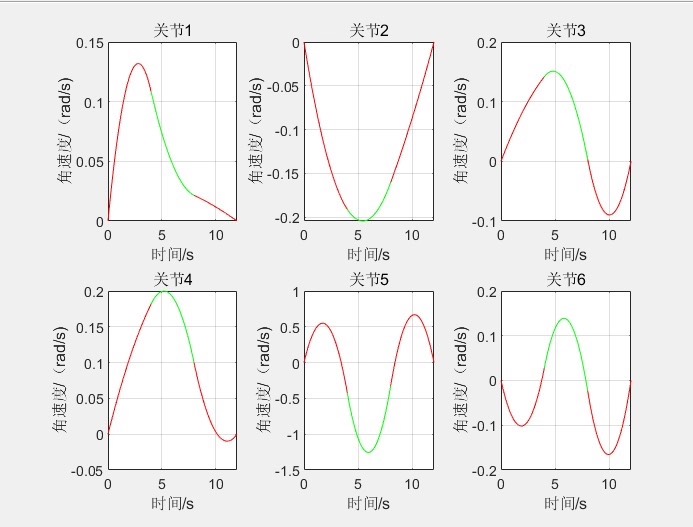
• 速度曲线：速度曲线在起始和结束阶段逐渐变化，避免了突变，保证了运动的平滑性。
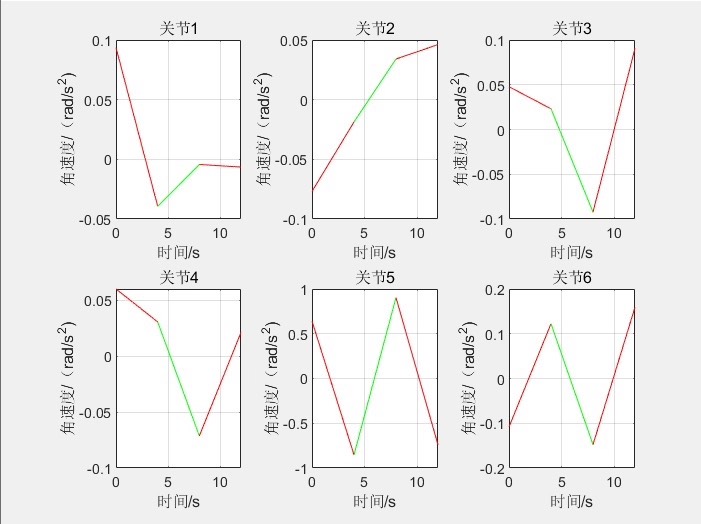
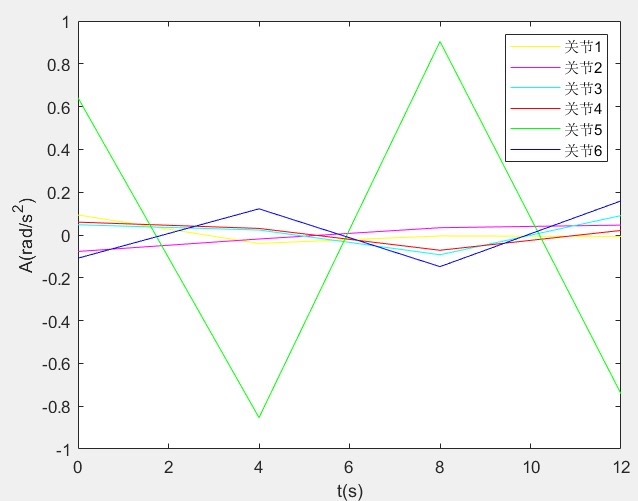
• 加速度曲线：加速度变化也表现出良好的连续性和平滑性，防止突然的冲击和振动。

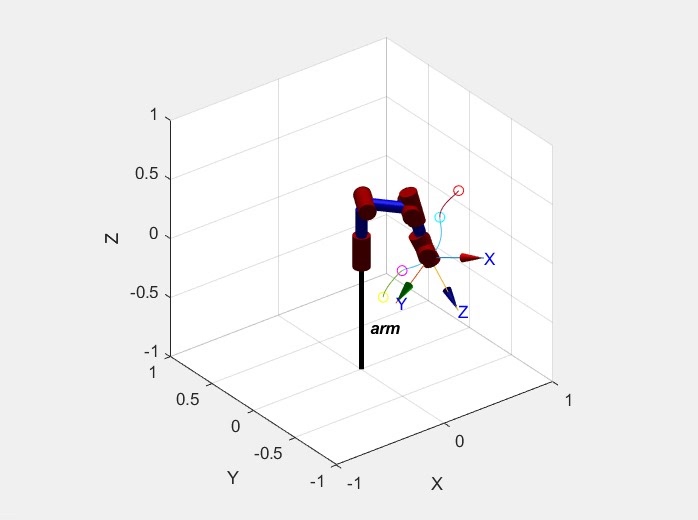
此外，通过MATLAB的三维可视化功能，还可以实时观察机械臂的运动轨迹。这种可视化方法对于验证轨迹规划的正确性和实用性非常重要。

自行更换参数

在实际应用中，可以根据具体需求调整机械臂的参数，例如起点和目标点的位置、速度和加速度的最大限制等。通过调整代码中的相关参数，可以适应不同的应用场景。

总结

3-3-3分段多项式插值法是一种高效且实用的机械臂轨迹规划方法。本文通过MATLAB进行了仿真建模，并展示了轨迹规划的可视化结果。这种方法不仅能够保证机械臂的运动平滑性，还能够满足实时控制的要求，非常适合于工业机器人和伺服系统的应用场景。如果你对机械臂的轨迹规划感兴趣，不妨动手尝试一下，调整不同的参数，看看会对结果产生什么样的影响！